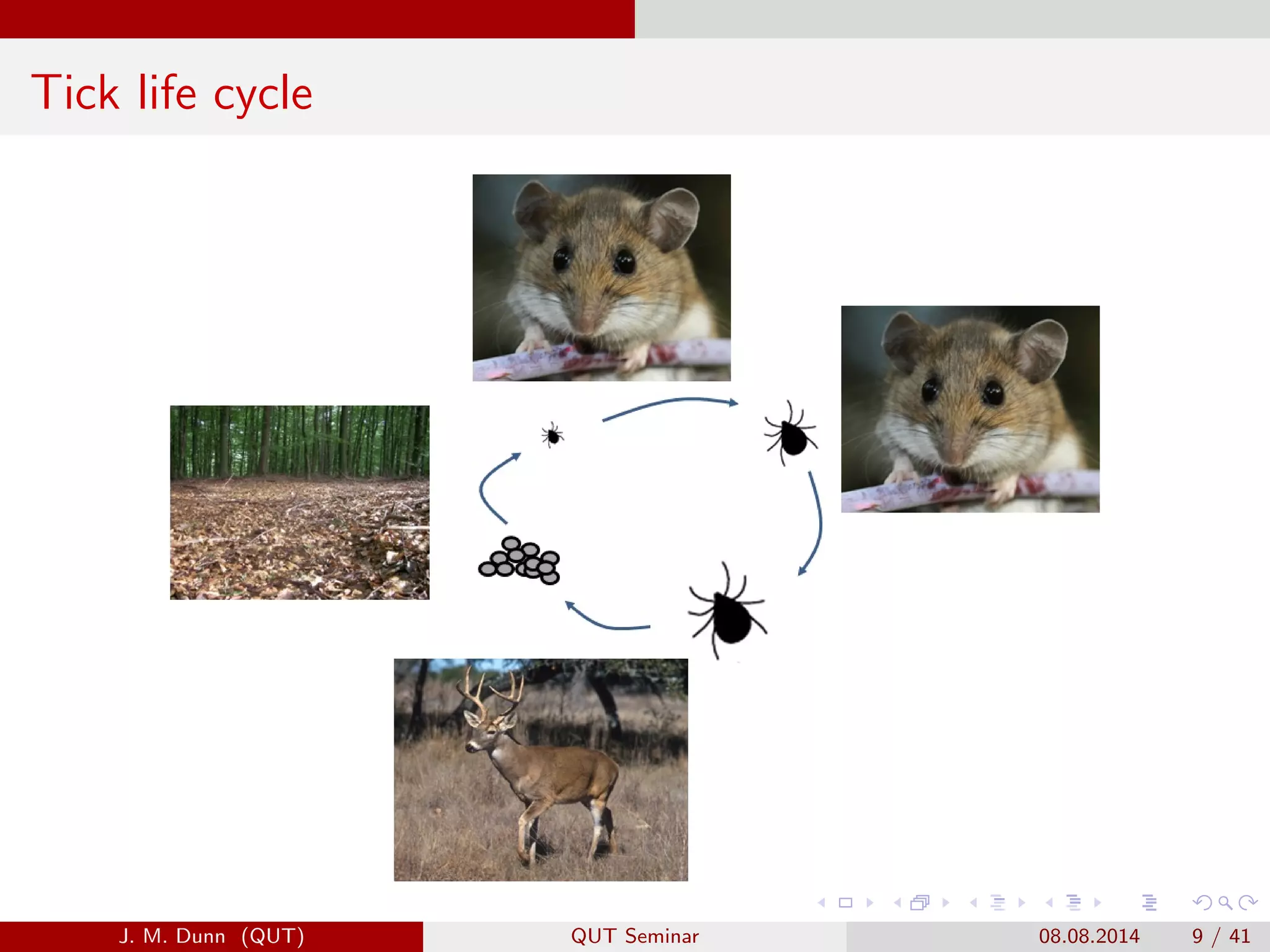
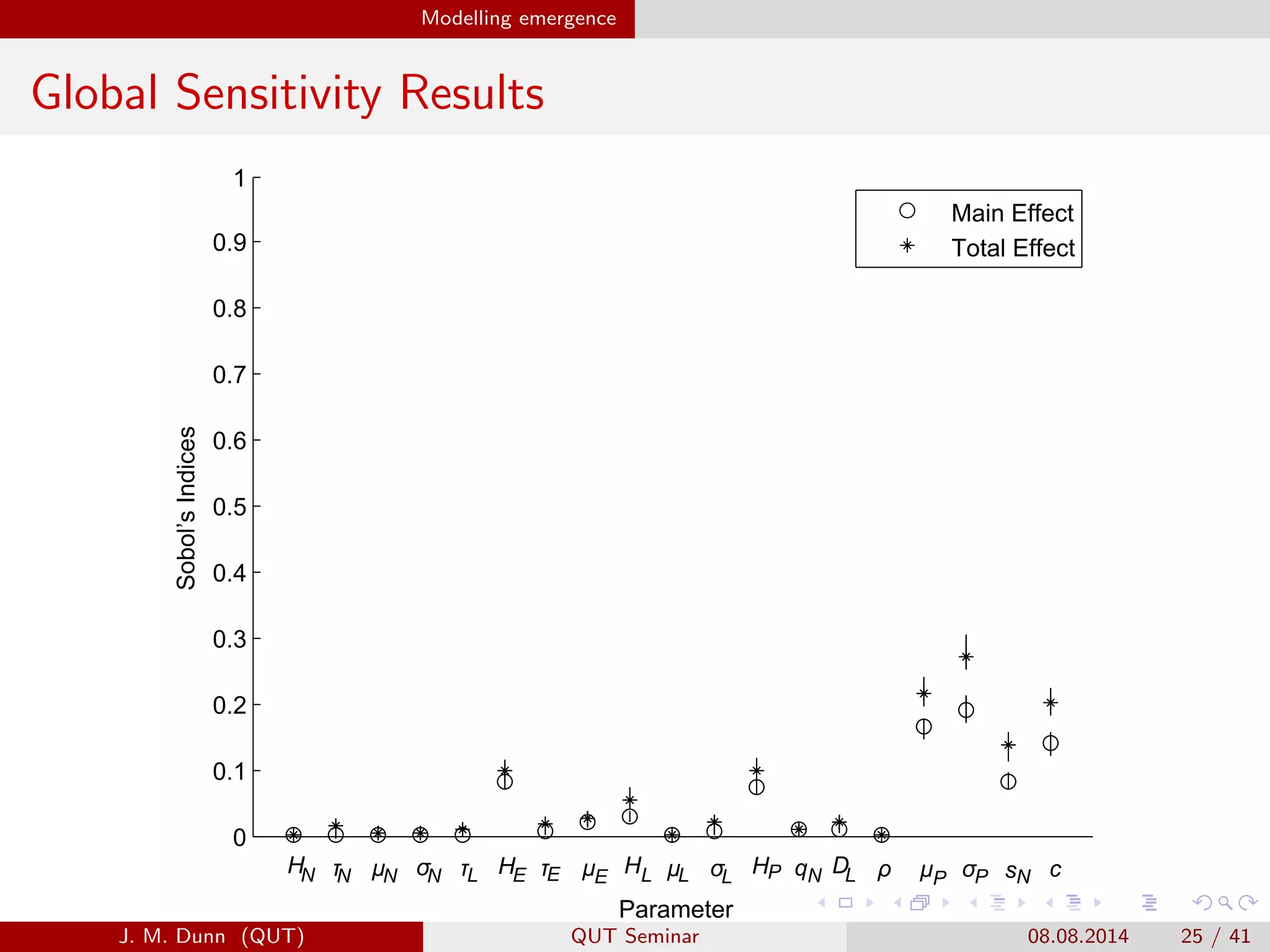
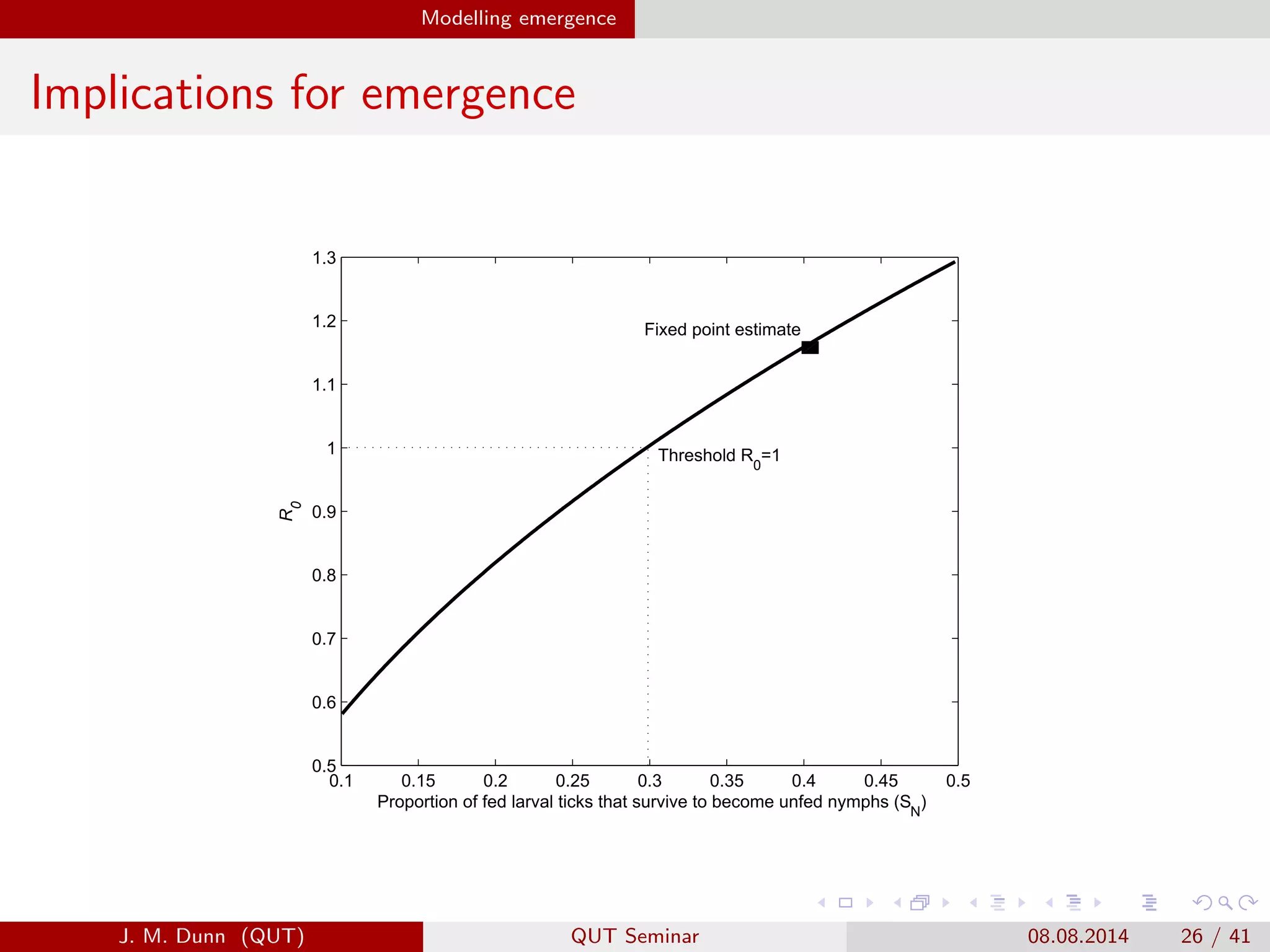
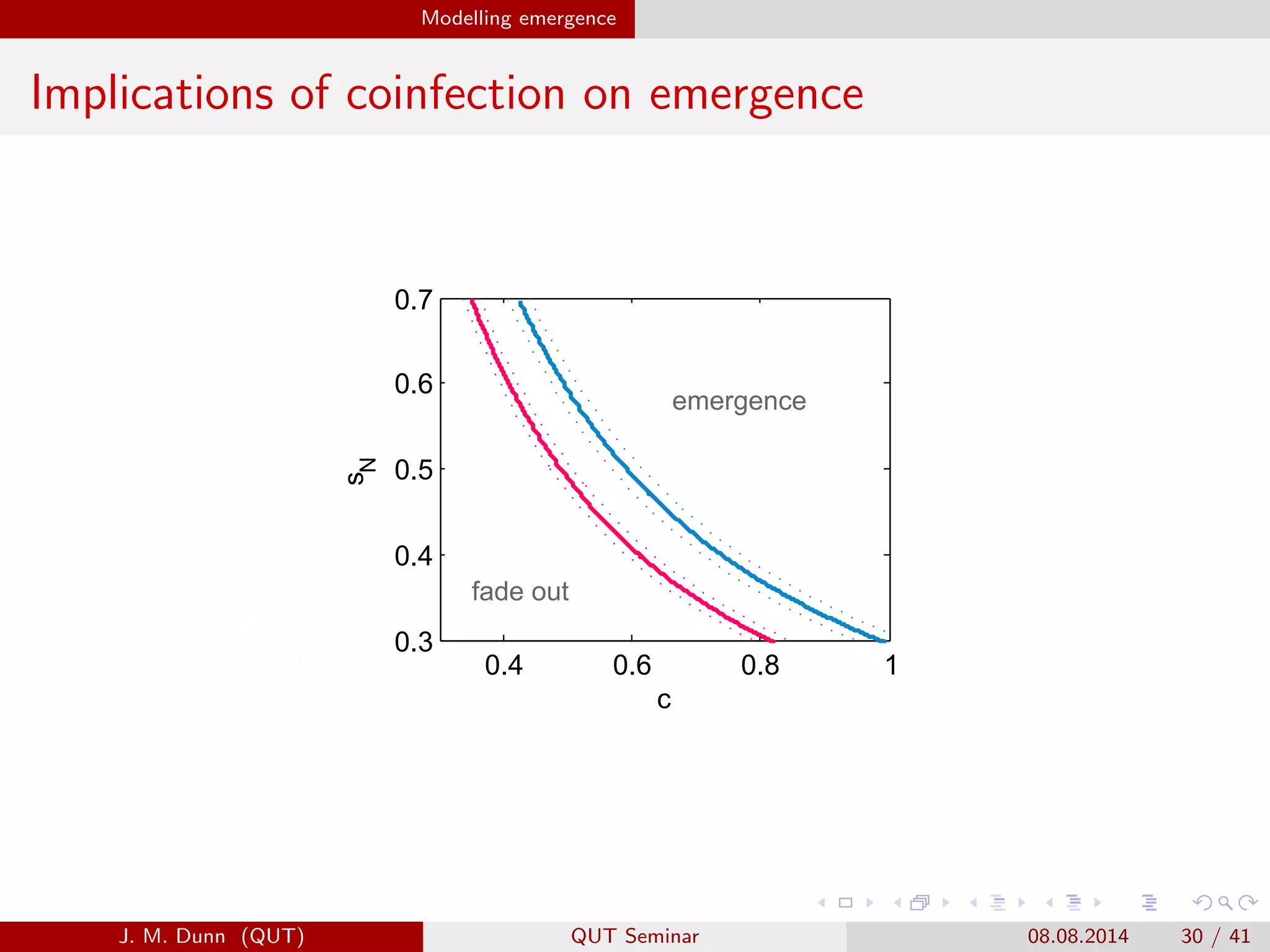
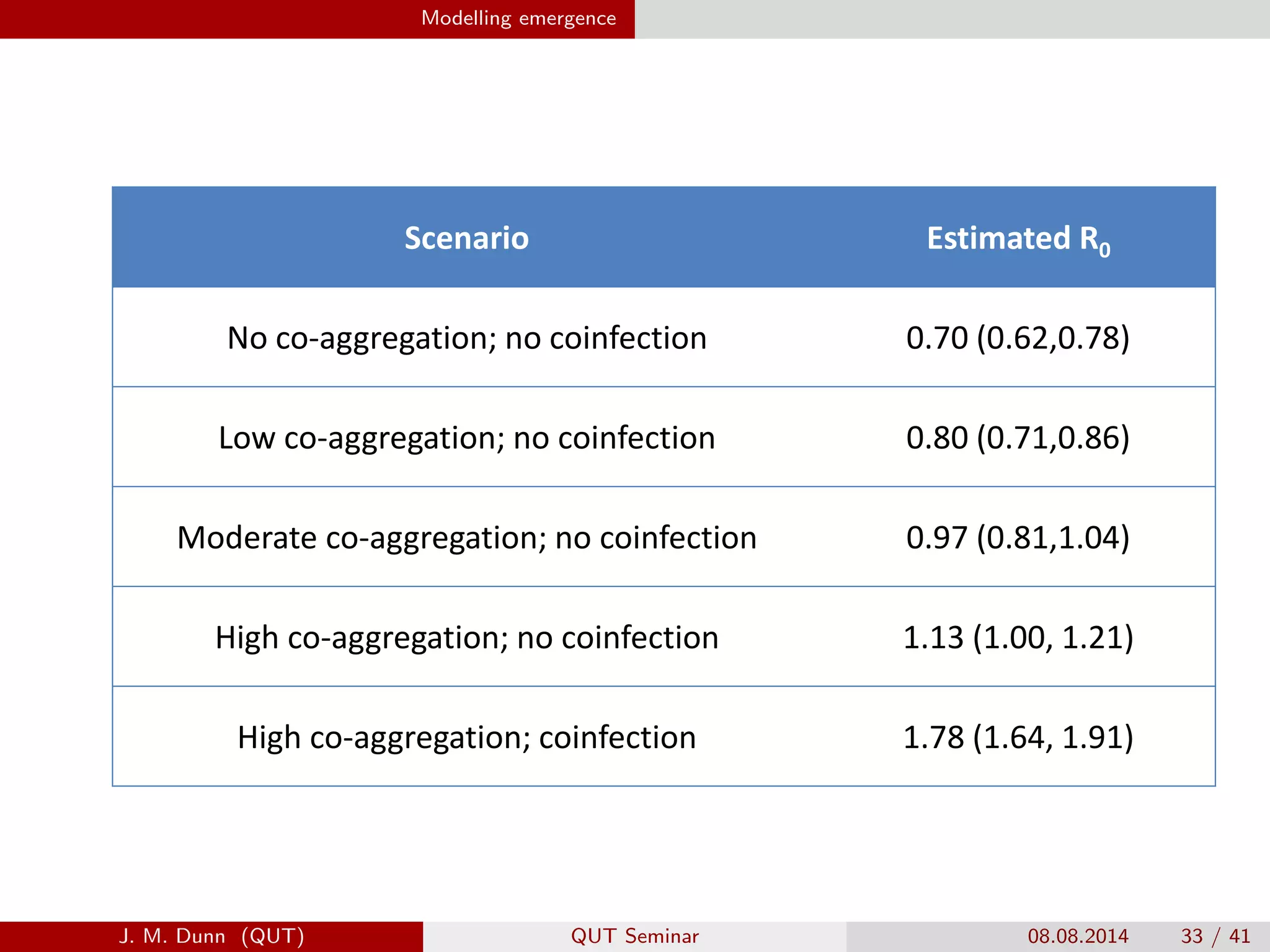
This document discusses the mathematical modeling of human babesiosis and Lyme disease in the northeastern United States, focusing on the complexities of tick-borne disease transmission. It highlights the challenges in developing accurate models due to varying hosts, tick life cycles, and transmission routes, while also addressing the implications of co-infection and host aggregation on disease emergence. The research aims to identify key factors facilitating disease spread and inform potential control measures.