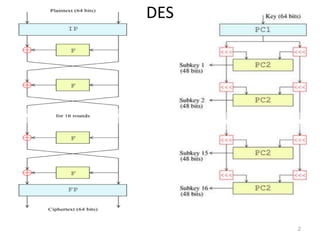
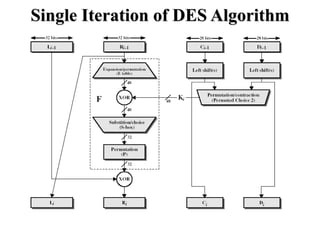
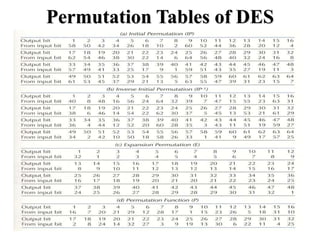
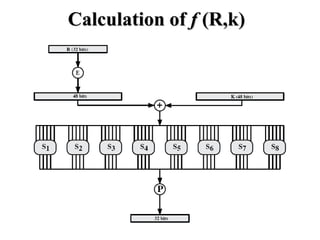
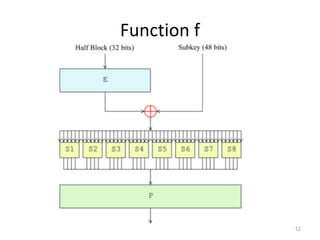
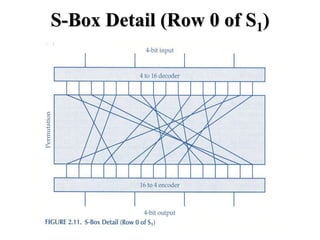
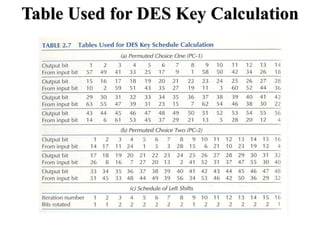
The document discusses the Data Encryption Standard (DES) algorithm. It was adopted in 1977 and encrypts 64-bit blocks using a 56-bit key. The algorithm uses permutations and substitutions to encrypt data in multiple rounds. Weak keys that reduce the algorithm's security are identified. Attacks like differential and linear cryptanalysis have been developed against DES. Alternatives like triple DES and extending the key length were proposed to strengthen it against attacks.

1. Data Encryption Standard (DES)
• Most widely used block cipher in the world
• Adopted in 1977 by National Bureau
Standards (NBS)
• Encrypts 64-bit data using 56-bit key
• Has widespread use
• Has been considerable controversy over its
security

2. 2
DES

3. Details of A Single Iteration
• First the left and right half of each 64-bit are
treated as separate 32-bit quantities labelled L
(left) and R (Right).
• The overall process at each iteration can be
summarized in:
Where denotes the bitwise XOR function
)
,
( 1
1
1
i
i
i
i
i
i
K
R
f
L
R
R
L








4. Single Iteration of DES Algorithm

5. Algorithm in Details
Initial Permutation (see the permutation tables)
• The output bit 1 for example is the input bit
58
• If we take the inverse permutation:
It can be seen that the original ordering is
restored.
)
(M
IP
X 
))
(
(
)
( 1
1
M
IP
IP
X
IP
Y 




6. Permutation Tables of DES

7. Calculation of f (R,K) and S-Boxes
• First R input is expanded to 48 bit to be equal
to the iteration key by using the permutation
table.
• The resulting 48-bit of R is XOR ed with the
key and the result passes through a substitution
function (S-box) that produces 32-bit output.
• The 32-bit output is permuted as defined in the
permutation table also to produce the output.
i
K
i
K

8. Calculation of f (R,k)

9. S-Box Detail
• The input to each S-Box is 6 bits and the
output is 4 bits.
• The first and last bits of the input to box
from a 2-bit binary number to select a
particular row in the DES S-Box table.
• The middle 4 bit selects a particular column.
• The decimal value in the selected cell is
converted to a 4-bit binary output
i
S

10. Continue…
Example
• The input of 011011, the row is 01(row 1).
• The column is 1101 (column 13).
• The value in the row 1 and column 13 in the S-Box
table cell is 5 , so the output is (0101).
• The first and the last bit of the output select one of
four permutations for rows of the S-Box table

11. Definition of DES S-Boxes

12. 12
Function f

13. S-Box Detail (Row 0 of S1)

14. Cryptography and Network Security 14
Sub-key Generation
• Given a 64 bits key (with parity-check bit)
– Discard the parity-check bits
– Permute the remaining bits using fixed table P1
– Let C0D0 be the result (total 56 bits)
• Let Ci =Shifti(Ci-1); Di =Shifti(Di-1) and Ki be
another permutation P2 of CiDi (total 56
bits)
– Where cyclic shift one position left if i=1,2,9,16
– Else cyclic shift two positions left
Key Generation

15. Key Generation
• First the 56-bit key is subjected to a
permutation governed by the DES key
calculation table.
• Then the 56-bit is treated as 28-bit quantities
labelled Co and Do.
• C and D are separately subjected to a circular
shift or rotation of 1 or 2 bit governed by the
DES key calculation table.
• They are also serve as input to another
permutation to produce the 48-bit output.

16. Table Used for DES Key Calculation

17. Cryptography and Network Security 17
DES Weak Keys
• With many block ciphers there are some
keys that should be avoided, because of
reduced cipher complexity
• These keys are such that the same sub-key
is generated in more than one round, and
they include:

18. Cryptography and Network Security 18
Continue….
• Weak keys
– The same sub-key is generated for every round
– DES has 4 weak keys
• Semi-weak keys
– Only two sub-keys are generated on alternate
rounds
– DES has 12 of these (in 6 pairs)
• Demi-semi weak keys
– Have four sub-keys generated

19. Cryptography and Network Security 19
Continue….
• None of these causes a problem since they
are a tiny fraction of all available keys
• However they MUST be avoided by any key
generation program

20. DES Decryption
• The process of decryption is the same as the
encryption process.
• The rule is as follows: use the cipher text as
input to the DES algorithm but use the keys
in reverse order. That is use on the first
iteration and on the second and son on
i
K
16
K
15
K

21. DES Encryption and Decryption

22. 22
DES in Practice
• DEC (Digital Equipment Corp. 1992) built a
chip with 50k transistors
– Encrypt at the rate of 1G/second
– Clock rate 250 Mhz
– Cost about $300
• Applications
– ATM transactions (encrypting PIN and so on)

23. The Strength of DES
• Concerns about the strength of DES fall into two
categories:
–Concerns about the algorithm itself (nothing so
far).
–Concerns about the use of 56-bit key.
• Electronic Frontier Foundation (EFF) announced
that it had broken a new DES encryption using a
“DES Cracker” machine for less than $250,000.
• A 128 bit key is guaranteed for unbreakable
algorithm by Brute-Force.

24. Time To Break A Code
(106 decryption/ s)

25. Cryptography and Network Security 25
DES Attacks
1998:
The EFF's US$250,000
DES cracking machine
contained 1,536 custom chips
and could brute force a DES key in a
matter of days —
the photo shows a DES Cracker
circuit board fitted
with several Deep Crack chips.

26. Cryptography and Network Security 26
DES Attacks:
The COPACOBANA machine,
built for US$10,000 by the
Universities of Bochum and
Kiel, contains 120 low-cost
FPGAs and can perform an
exhaustive key search on
DES in 9 days on average.
The photo shows the
backplane of the machine
with the FPGAs

27. Cryptography and Network Security 27
Attack Faster than Brute Force
• Differential cryptanalysis
– was discovered in the late 1980s by Eli Biham and Adi Shamir, although
it was known earlier to both IBM and the NSA and kept secret. To
break the full 16 rounds, differential cryptanalysis requires 247 chosen
plaintexts. DES was designed to be resistant to DC.
• Linear cryptanalysis
– was discovered by Mitsuru Matsui, and needs 243 known plaintexts
(Matsui, 1993); the method was implemented (Matsui, 1994), and was
the first experimental cryptanalysis of DES to be reported. There is no
evidence that DES was tailored to be resistant to this type of attack.

28. 28
Possible Techniques for Improving DES
• Multiple enciphering with DES
• Extending DES to 128-bit data paths and 112-bit
keys
• Extending the key expansion calculation

29. Double DES
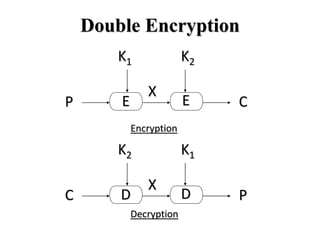
• The simplified form of multiple encryption has
two encryption stage and two keys.
• Given a plaintext P and two keys K1 and K2
one can generate a cipher text C as:
Decryption equation is :
• The key length is 562= 112 bits
]]
[
[ 1
2
P
E
E
C K
K

]]
[
[ 2
1
C
D
D
P K
K


30. Double Encryption
E E C
P
X
K1 K2
Encryption
D D P
C
X
K2 K1
Decryption

31. Cryptography and Network Security 31
Double DES
• Using two encryption stages and two keys
– C=Ek2(Ek1(P))
– P=Dk1(Dk2(C))
• It is proved that there is no key k3 such that
– C=Ek2(Ek1(P))=Ek3(P)
• But Meet-in-the-middle attack

32. Cryptography and Network Security 32
Meet-in-the-Middle Attack
• Assume C=Ek2(Ek1(P))
• Given the plaintext P and ciphertext C
• Encrypt P using all possible keys k1
• Decrypt C using all possible keys k2
– Check the result with the encrypted plaintext
lists
– If found match, they test the found keys again
for another plaintext and ciphertext pair
– If it turns correct, then find the keys
– Otherwise keep decrypting C

33. Continue….
• Given a known pair (P,C), the attack proceeds
as follows:
• Encrypt all the 256 possible values of K1store
the results in a table.
• Next decrypt C using all the 256 possible
values of K2 .
• Check the matching between the two tables. If
the matching occurs then you recognized the
two keys.

34. Cryptography and Network Security 34
Triple DES
• DES variant
• Standardized in ANSI X9.17 & ISO 8732 and
in PEM for key management
• Proposed for general EFT standard by ANSI
X9
• Backwards compatible with many DES
schemes
• Uses 2 or 3 keys

35. Cryptography and Network Security 35
Continue….
• No known practical attacks
• Brute force search impossible (very hard)
• Meet-in-the-middle attacks need 256
Plaintext-Cipher text pairs per key
• Popular current alternative