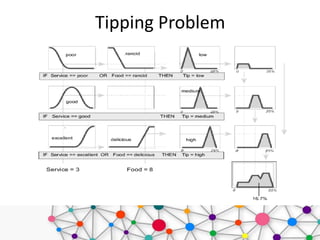
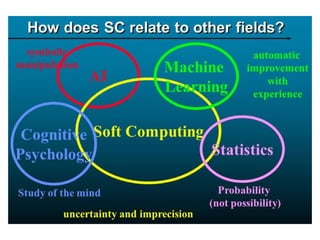
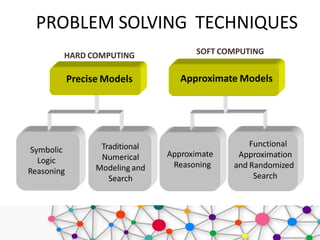
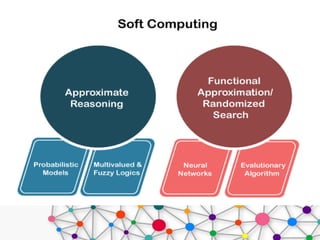
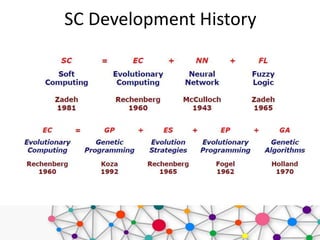
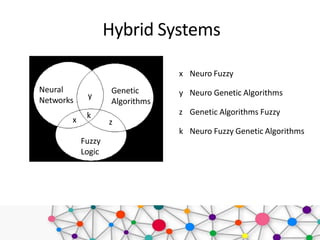
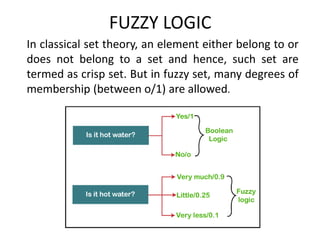
Soft computing is an approach that models cognitive behavior, allowing for solutions to complex problems that traditional hard computing cannot address due to imprecision and uncertainty. It employs methods like neural networks, fuzzy logic, and genetic algorithms to tackle real-world challenges efficiently. Applications of soft computing span various domains, including gaming, home appliances, robotics, and more, emphasizing its utility in managing ambiguous data and approximations.

1. Soft Computing: An Overview
Arpana Sinhal
Asst. Professor,
Department of Computer Science & Engineering
AIETM, Jaipur

2. Soft Computing, What is it?
• The idea behind soft computing is to model cognitive
behavior of human mind.
• Soft computing is foundation of conceptual intelligence
in machines.
• Use inexact solution to computationally hard tasks (such as
solution for NP-Complete problems, for which there is no known
algorithm that can compute an exact solution in polynomialtime)
• Unlike hard computing, Soft computing is tolerant of
imprecision, uncertainty, partial truth, and approximation.

3. • The idea of softcomputing was initiated in 1981 when
Lofti A. Zadeh published his first paper on soft data
analysis “What is softcomputing”, softcomputing.
Springer-Verlag Germany/ USA.
SoftComputing, What isit?
Lofti A. Zedah, 1992:
“Softcomputing is an emerging approach to computing which
parallel the remarkable ability of human mind to reason and learn
in the environment of uncertainly and imprecision”

5. PROBLEM SOLVING TECHNIQUES
Symbolic
Logic
Reasoning
Traditional
Numerical
Modeling and
Search
Approximate
Reasoning
Functional
Approximation
and Randomized
Search
SOFT COMPUTING
HARD COMPUTING
Precise Models Approximate Models

6.  Hard computing
Deals with precise values
Accurate output is needed
Useful in critical systems
 Soft computing
 Deals with assumptions
Accuracy is not necessary
Useful for routine,control, decison making tasks
Hard Vs Soft Computing

7. Hard Vs Soft Computing
Hard Computing Soft Computing
Conventionalcomputing requiresa precisely
statedanalyticalmodel.
Softcomputing istolerant ofimprecision.
Often requiresalot of computationtime. Can solve some real world problems
in reasonablylesstime.
Not suited for real world problems for
which ideal model isnotpresent.
Suitablefor real worldproblems.
It requiresfulltruth Canwork with partialtruth
It isprecise andaccurate Imprecise.
Highcostfor solution Lowcostfor solution
Requireprogramsto bewritten Canevolveits own programs
Deterministic Stochasticorrandom
Requireexactinput Candealwith ambiguousandnoisydata
Produceprecise answer Produceapproximateanswers
usestwo-valuedlogic. canusemultivaluedorfuzzy logic

8. Aims of Soft Computing
• The main goal of soft computing is to develop intelligent
machines that provide solutions for real world problems,
which are not modeled/too difficult to model mathematically.
• It’s aim is to exploit the tolerance for Approximation,
Uncertainty, Imprecision, and Partial Truth in order to
achieve close resemblance with human like decision making.
• The guiding principle of soft computing is to exploit these
tolerance to achieve tractability, robustness and low solution
cost.
• The role model for soft computing is the human mind.

9.  Models based on human reasoning.
 Closer to human thinking and biologically
inspired
 Models can be
 Linguistic
 Comprehensible
 Fast when computing
 Effective in practice.
Advantages of Soft Computing

11. Applications of soft computing
There are several applications of soft computing where it is used.
Some of them are listed below:
• It is widely used in gaming products like Poker and Checker.
• In kitchen appliances, such as Microwave and Rice cooker.
• In most used home appliances - Washing Machine, Heater,
Refrigerator, and AC as well.
• Apart from all these usages, it is also used in Robotics
work (Emotional per Robot form).
• Image processing and Data compression are also popular
applications of soft computing.
• Used for handwriting recognition.
As we already said that, soft computing provides the solution to
real-time problems and here you can see that. Besides these
applications, there are many other applications of soft computing.

12. Soft Computing Components
Neural Networks
Neural Networks mimic certain processing capabilities of the human
brain and used for learning and adaption.
Fuzzy Logic
Multivalued Logic for treatment of imprecision and vagueness which
used for knowledge representation via fuzzy if-then rules.
Genetic Algorithms
Genetic Algorithms (GAs) are used for evolutionary computation and
to mimic some of the processes observed in natural evolution.

13. Heavy industry
• Robotic arms, Humanoid robots
Home appliances
• Washing machines, ACs,
Refrigerators, cameras
Automobiles
• Travel Speed Estimation, Sleep
Warning Systems, Driver-less cars
Spacecrafts
Maneuvering of a Space Shuttle (FL),
Optimization of Fuel-efficient Solutions for
space craft
APPLICATIONS OF SOFT COMPUTING

14. These methods have in common that :
• they are nonlinear,
• have ability to deal with non-linearities,
• follow more human-like reasoning paths than classical methods,
• utilize self-learning,
• utilize yet-to-be-proven theorems,
• are robust in the presence of noise or errors.
Soft computing is not a concoction, mixture, or combination, rather,
Soft computing is a partnership in which each of the partners
contributes a distinct methodology for addressing problems in its
domain.
In principal the constituent methodologies in Soft computing are
complementary rather than competitive.
Soft Computing Constituents

15. SC Development History

16. Hybrid Systems
Neural
Networks
Genetic
Algorithms
Fuzzy
Logic
x
y
z
k
x Neuro Fuzzy
y Neuro Genetic Algorithms
z Genetic Algorithms Fuzzy
k Neuro Fuzzy Genetic Algorithms

17. • Fuzzy set theory proposed in 1965 by Lotfi A.
Zadeh is a generalization of classical set theory.
• Uses numeric ranges of sets (fuzzy sets ) to
measure and represent the logical evaluations
of partially accurate findings.
• Most applications in control and decision
making.
FUZZY LOGIC

18. FUZZY LOGIC
In classical set theory, an element either belong to or
does not belong to a set and hence, such set are
termed as crisp set. But in fuzzy set, many degrees of
membership (between o/1) are allowed.

19. Fuzzy mathematics and Fuzzy Set Theory
• Fuzzy mathematics is the branch of mathematics including fuzzy set theory and
fuzzy logic that deals with partial inclusion of elements in a set on a spectrum, as
opposed to simple binary "yes" or "no" (0 or 1) inclusion.
• It started in 1965 after the publication of Lotfi Asker Zadeh's seminal work Fuzzy
sets.t Set Th
• The word “Fuzzy means “ambiguity” Fuzzy set theory permits membership function
valued in the interval{0/1}
• Fuzzy sets can be considered as an extension and gross over simplification of
classical sets.
• It can be best understood in the context of set membership.
• Basically it allows partial membership which means that it contain elements that
have varying degrees of membership in the set. From this, we can understand the
difference between classical set and fuzzy set.
• Classical set contains elements that satisfy precise properties of membership while
fuzzy set contains elements that satisfy imprecise properties of membership.
•
or
• ory

20. Membership Functions

21. Basic concepts of Fuzzy Logics
• Support and Core of a Fuzzy Set
The support S(μ) of a fuzzy set μ ∈ F(X ) is the crisp set that
contains all elements of X that have nonzero membership. Formally
S(μ) = [μ] 0 = {x ∈ X | μ(x) > 0}.
The core C (μ) of a fuzzy set μ ∈ F(X ) is the crisp set that contains
all elements of X that have membership of one. Formally,
C (μ) = [μ] 1 = {x ∈ X | μ(x) = 1}.
Height of a Fuzzy Set
• Definition
The height h(μ) of a fuzzy set μ ∈ F(X ) is the largest membership
grade obtained by any element in that set. Formally,
h(μ) = sup μ(x).
• x ∈X
• h(μ) may also be viewed as supremum of α for which [μ]α is not equal to ∅.
• Definition
• A fuzzy set μ is called normal when h(μ) = 1.
• It is called subnormal when h(μ) < 1.
•

22. Properties of Fuzzy Sets

23. Fuzzy Relation
• Fuzzy relation operations are operations that are performed on
fuzzy relations. A fuzzy relation is a mathematical
representation of a relationship between objects where the
degree of the relationship is expressed as a value between 0
and 1. Some common fuzzy relation operations include
composition, union, intersection, and complement. These
operations allow for the manipulation of fuzzy relations in order
to reason about uncertainty and imprecision in data.

24. Operations on Fuzzy Set
1.Union Operation: The union operation of a fuzzy set is defined by:
μA∪B(x) = max (μA(x), μB(x))
2
2. Intersection Operation:The intersection operation of fuzzy set is defined by:
μA∩B(x) = min (μA(x), μB(x))
3. Complement Operation: The complement operation of fuzzy set is defined by:
μĀ(x) = 1-μA(x),

25. Tipping Problem

26. FUTURE SCOPE
• Soft Computing can be extended to include
bio-informatics aspects.
• Fuzzy system can be applied to the construction
of more advanced intelligent industrial systems.
• Soft computing is very effective when it’s applied
to real world problems which are not able to
solved by traditional hard computing.