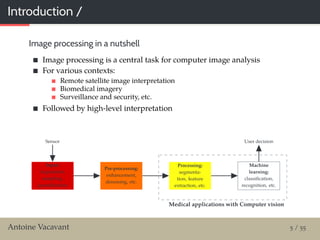
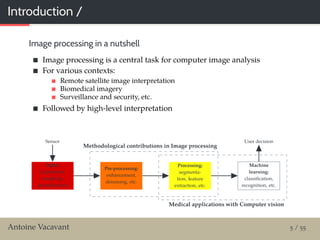
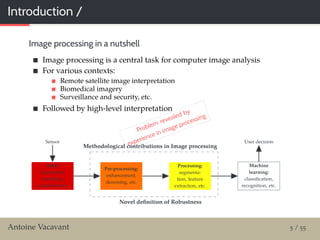
This document summarizes a seminar presentation about robust image processing algorithms involving tools from digital geometry and mathematical morphology. The presentation introduces the speaker and their background and research interests. It then discusses the need for a formal definition of robustness for image processing algorithms. Such a definition is proposed, involving evaluating algorithms over multiple noise scales and ensuring quality measures respect Lipschitz continuity as noise increases. Examples are given of algorithms from mathematical morphology and digital geometry that have been evaluated for robustness based on this definition. The talk concludes by discussing applications of these techniques to biomedical image analysis tasks.














![Definition of robustness / Robustness for image processing
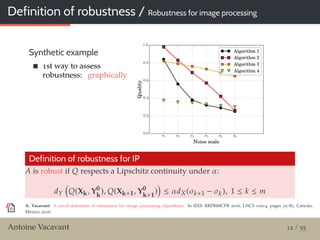
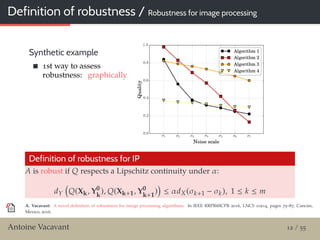
Contribution
Propose a definition of robustness for IP algorithms
In parallel of what has been done in CV
Presented at CBA in 2016
Input noise model
We suppose that the input data is altered with an additive
noise, with similar notations as [Meer, 2001]
yi y0
i
+ δyi , yi ∈ Rq
, i 1, . . . , n
also shortened as
Y Y0
+ δY
Antoine Vacavant 10 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-19-320.jpg)
![Definition of robustness / Robustness for image processing
Contribution
Propose a definition of robustness for IP algorithms
In parallel of what has been done in CV
Presented at CBA in 2016
Input noise model
We suppose that the input data is altered with an additive
noise, with similar notations as [Meer, 2001]
yi y0
i
+ δyi , yi ∈ Rq
, i 1, . . . , n
also shortened as
Y Y0
+ δY
With
Y: measurements
Y0: true (and generally unknown) value
δY: corruption by the noise
We can suppose wlog an iid noise as δyi GI(0, σ2Cy)Antoine Vacavant 10 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-20-320.jpg)





![MM / Context and motivation
Image denoising filtering
A lot of contributions since 70’s [Lebrun et al., 2012]
Linear, popular, simple filters: Gaussian, average, median, bilateral, etc.
Non-local strategies: NL-means, BM3D, total variation, etc.
PDE schemes: anisotropic diffusion, coherence, etc.
Antoine Vacavant 15 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-34-320.jpg)
![MM / Context and motivation
Image denoising filtering
A lot of contributions since 70’s [Lebrun et al., 2012]
Linear, popular, simple filters: Gaussian, average, median, bilateral, etc.
Non-local strategies: NL-means, BM3D, total variation, etc.
PDE schemes: anisotropic diffusion, coherence, etc.
Shock filtering
Shock filter iteratively produces local segmentations in inflection zones:
∆ f t−1(pi , qj) < 0 ⇒ f t(pi , qj) f t−1(pi , qj) ⊕ D ;
∆ f t−1(pi , qj) > 0 ⇒ f t(pi , qj) f t−1(pi , qj) D
Antoine Vacavant 15 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-35-320.jpg)
![MM / Context and motivation
Image denoising filtering
A lot of contributions since 70’s [Lebrun et al., 2012]
Linear, popular, simple filters: Gaussian, average, median, bilateral, etc.
Non-local strategies: NL-means, BM3D, total variation, etc.
PDE schemes: anisotropic diffusion, coherence, etc.
Shock filtering
Shock filter iteratively produces local segmentations in inflection zones:
∆ f t−1(pi , qj) < 0 ⇒ f t(pi , qj) f t−1(pi , qj) ⊕ D ;
∆ f t−1(pi , qj) > 0 ⇒ f t(pi , qj) f t−1(pi , qj) D
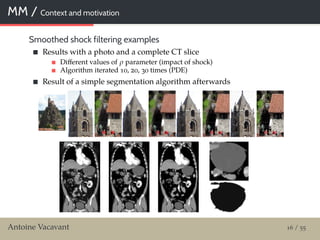
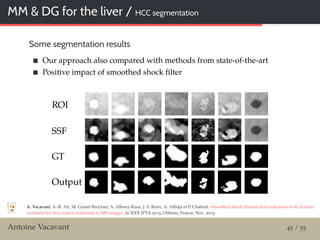
Smoothed shock filtering
Enhance contours by creating smoothed ruptures
PDE scheme with smoothed ⊕, operators
A. Vacavant, A. Albouy-Kissi, P.-Y. Menguy, J. Solomon: Fast smoothed shock filtering. In IEEE ICPR 2012, Tsukuba, Japan, 2012.
Antoine Vacavant 15 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-36-320.jpg)


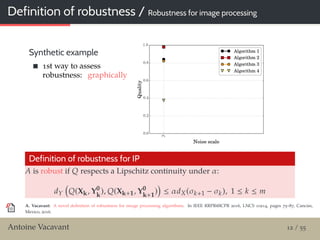
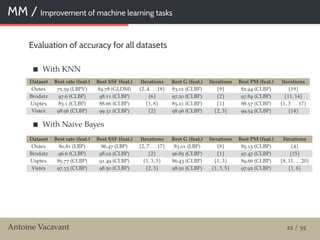
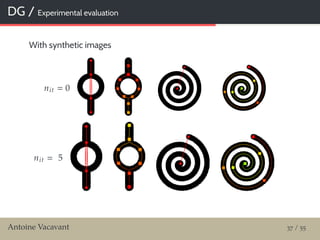
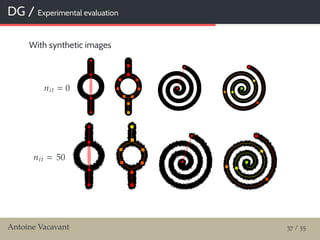
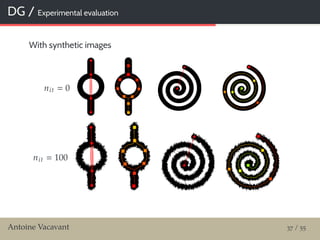
![MM / Test of robustness
Material and methods
13 classic images / Y0
Altered with additive white Gaussian noise / Y
With increasing std / scales {σk }k 1,5 {5, 10, 15, 20, 25}
From state of the art
Shock-based methods
Classic algorithms
Median-based methods
Algorithm Reference
Median [Huang et al., 1979]
Coherence [Weickert, 2003]
OriginalShock [Osher and Rudin, 1990]
EnhancedShock [Alvarez and Mazorra, 1994]
ComplexShock [Gilboa et al., 2004]
Bilateral [Tomasi and Manduchi, 1998]
SmoothedMedian [Kass and Solomon, 2010]
SmoothedShock [Vacavant et al., 2012]
Antoine Vacavant 18 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-40-320.jpg)
![MM / Test of robustness
Experimental results
Quality measure: SSIM / Structural similarity [Wang et al., 2004]
A. Vacavant: A novel definition of robustness for image processing algorithms. In IEEE RRPR@ICPR 2016, LNCS 10214, pages 75–87, Cancún,
Mexico, 2016.
Antoine Vacavant 19 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-41-320.jpg)
![MM / Test of robustness
Experimental results
Quality measure: SSIM / Structural similarity [Wang et al., 2004]
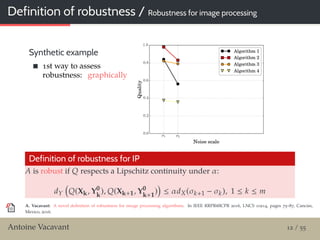
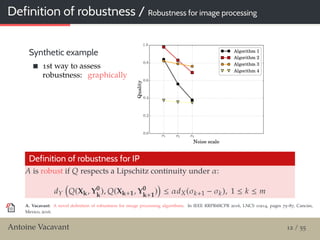
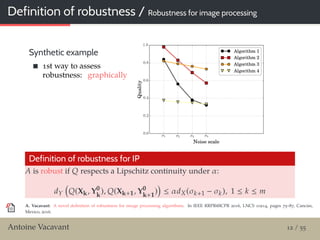
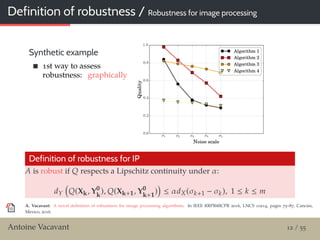
Graphical evaluation of robustness
A. Vacavant: A novel definition of robustness for image processing algorithms. In IEEE RRPR@ICPR 2016, LNCS 10214, pages 75–87, Cancún,
Mexico, 2016.
Antoine Vacavant 19 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-42-320.jpg)
![MM / Test of robustness
Experimental results
Quality measure: SSIM / Structural similarity [Wang et al., 2004]
Graphical evaluation of robustness
A. Vacavant: A novel definition of robustness for image processing algorithms. In IEEE RRPR@ICPR 2016, LNCS 10214, pages 75–87, Cancún,
Mexico, 2016.
Antoine Vacavant 19 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-43-320.jpg)
![MM / Test of robustness
Experimental results
Quality measure: SSIM / Structural similarity [Wang et al., 2004]
Graphical evaluation of robustness
A. Vacavant: A novel definition of robustness for image processing algorithms. In IEEE RRPR@ICPR 2016, LNCS 10214, pages 75–87, Cancún,
Mexico, 2016.
Antoine Vacavant 19 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-44-320.jpg)
![MM / Test of robustness
Experimental results
Quality measure: SSIM / Structural similarity [Wang et al., 2004]
Graphical evaluation of robustness
A. Vacavant: A novel definition of robustness for image processing algorithms. In IEEE RRPR@ICPR 2016, LNCS 10214, pages 75–87, Cancún,
Mexico, 2016.
Antoine Vacavant 19 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-45-320.jpg)
![MM / Test of robustness
Experimental results
Quality measure: SSIM / Structural similarity [Wang et al., 2004]
Graphical evaluation of robustness
A. Vacavant: A novel definition of robustness for image processing algorithms. In IEEE RRPR@ICPR 2016, LNCS 10214, pages 75–87, Cancún,
Mexico, 2016.
Antoine Vacavant 19 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-46-320.jpg)
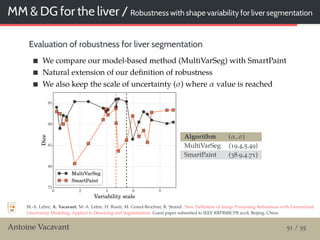
![MM / Test of robustness
Experimental results
Quality measure: SSIM / Structural similarity [Wang et al., 2004]
Graphical evaluation of robustness
Numerical evaluation of robustness
Algorithm α
Median 0.15
Coherence 0.15
OriginalShock 0.14
EnhancedShock 0.14
ComplexShock 0.12
Bilateral 0.11
SmoothedMedian 0.05
SmoothedShock 0.04
A. Vacavant: A novel definition of robustness for image processing algorithms. In IEEE RRPR@ICPR 2016, LNCS 10214, pages 75–87, Cancún,
Mexico, 2016.
Antoine Vacavant 19 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-47-320.jpg)







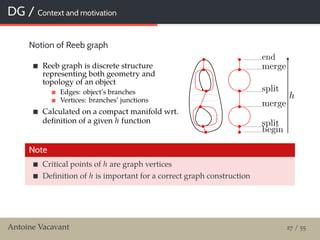
![DG / Context and motivation
Reeb graphs in literature
A lot of attention on its construction for 3-D
meshes [Biasotti et al., 2008; Harvey et al., 2010]
Generally, h is a height function (along an axis)
Appropriate for many objects, but not for all!
Can be calculated with other functions (e.g.
geodesic) [Tierny, 2006]
Antoine Vacavant 28 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-57-320.jpg)
![DG / Context and motivation
Reeb graphs in literature
A lot of attention on its construction for 3-D
meshes [Biasotti et al., 2008; Harvey et al., 2010]
Generally, h is a height function (along an axis)
Appropriate for many objects, but not for all!
Can be calculated with other functions (e.g.
geodesic) [Tierny, 2006]
Skeletons, medial axes and other 1-pixel-wide
centered structures capture topology [Arcelli et
al., 2010; Bertrand et al., 2014]
Strategy: Compute Reeb graph from such
structures [Janusch et al., 2015; Pascucci et al.,
2007]
Antoine Vacavant 28 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-58-320.jpg)
![DG / Context and motivation
Reeb graphs in literature
A lot of attention on its construction for 3-D
meshes [Biasotti et al., 2008; Harvey et al., 2010]
Generally, h is a height function (along an axis)
Appropriate for many objects, but not for all!
Can be calculated with other functions (e.g.
geodesic) [Tierny, 2006]
Skeletons, medial axes and other 1-pixel-wide
centered structures capture topology [Arcelli et
al., 2010; Bertrand et al., 2014]
Strategy: Compute Reeb graph from such
structures [Janusch et al., 2015; Pascucci et al.,
2007]
But they can be very sensitive to noise!
Linking them to Reeb graph is not trivial
Antoine Vacavant 28 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-59-320.jpg)


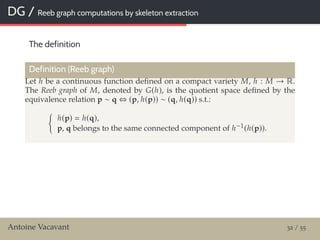
![DG / Reeb graph computations by skeleton extraction
DECS algorithm
DECS: Discrete Euclidean Connected Skeleton [Leborgne et al., 2015]
Resist to noise, compared to other algorithms
Antoine Vacavant 31 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-62-320.jpg)
![DG / Reeb graph computations by skeleton extraction
DECS algorithm
DECS: Discrete Euclidean Connected Skeleton [Leborgne et al., 2015]
Resist to noise, compared to other algorithms
Algorithm:
From a binary image I
Euclidean distance map EDTI
Reduced medial axis RDMAI
Laplacian-of-Gaussian filtering of EDTI as RDGI
Combine RDGI and RDMAI to calculate a coarse skeleton SI
Thin and prune SI to obtain S∗
I
EDTI RDMAI RDGI SI S∗
I
Antoine Vacavant 31 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-63-320.jpg)







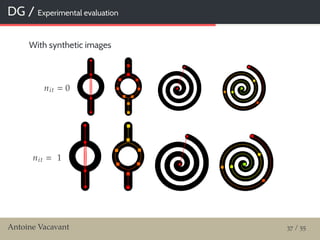









![MM & DG for the liver / Hepatic vascular network segmentation
Our pipeline for segmenting liver vessels
From a CT or MRI volume, I
Extract the liver and use it as a bounding box
Multi-scale vessel detection with Hessian matrix IS [Sato et al., 1994]
Partial skeletonization and reconnection S in IS [Homann et al., 2007]
Calculate the RORPO vesselness filter IR [Merveille et al., 2018]
Use S as initialization for fast marching segmentation within IR
M.-A. Lebre, A. Vacavant, M. Grand-Brochier, O. Merveille, A. Abergel, P. Chabrot, B. Magnin: Automatic 3-D Skeleton-based Segmentation of Liver
Vessels From MRI and CT for Couinaud Representation. In IEEE ICIP 2018, Athens, Greece,
Antoine Vacavant 47 / 55](https://image.slidesharecdn.com/talk-vacavant-cba-fall2018-181025053203/85/Robust-image-processing-algorithms-involving-tools-from-digital-geometry-and-mathematical-morphology-88-320.jpg)