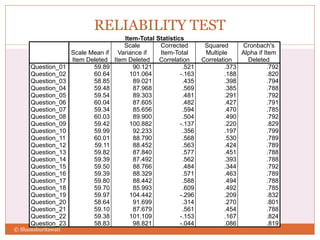
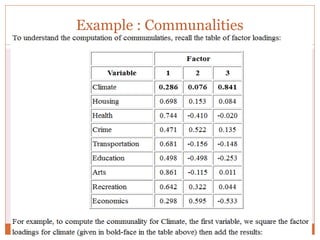
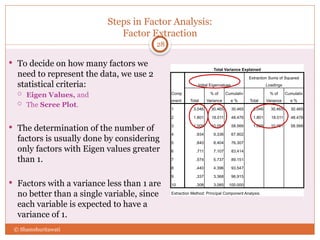
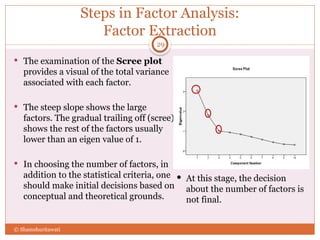
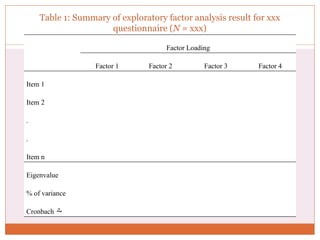
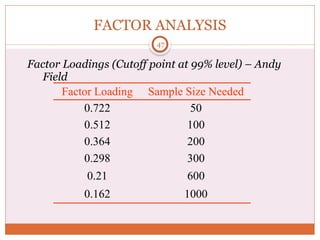
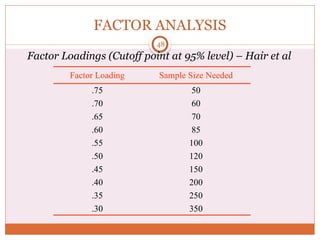
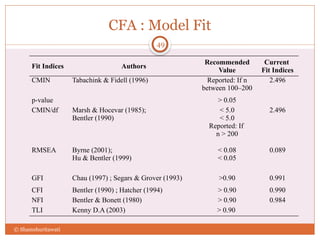
The document discusses reliability analysis with a focus on Cronbach's alpha, which is used as a measure of internal consistency for a set of items, indicating reliability when the value is 0.7 or higher. It also covers the application of factor analysis for data reduction and scale development, providing steps for conducting the analysis such as correlation matrix computation, factor extraction, and rotation methods. The document emphasizes the importance of adequate sample size and inter-item correlations in ensuring the validity of the measures.

1. Reliability Analysis
Presented by
Shamshuritawati Sharif
School of Quantitative Sciences
College of Arts and Sciences
1
© Shamshuritawati

2. RELIABILITY TEST
Cronbach’s alpha is most commonly used as a reliability
measure of a set of items (or statements).
This measure can be interpreted as a correlation
coefficient, and it’s value ranges from 0 to 1.
Items (statements) which are negatively worded must be
recoded before performing reliability analysis.
The set of items is said to be reliable or have internal
consistency if Cronbach’s alpha value is 0.7 or higher.
2
© Shamshuritawati

3. RELIABILITY TEST
However, Cronbach alpha is quite sensitive to the number of
items in the scale.
If Cronbach alpha is small, report the mean inter-item
correlation for the items.
Briggs and Cheek (1986) recommend an optimal range for
the inter-item correlation of 0.2 to 0.4.
If the result is still not promising, carry out factor analysis
to isolate multi dimensions or distinct components.
Recompute alpha for each component identified.
3
© Shamshuritawati

4. Example : SAQ. (Item 3 reversed).sav
1. Statistics makes me cry
2. My friends will think I'm stupid for not being able to cope with SPSS
3. Standard deviations excite me
4. I dream that Pearson is attacking me with correlation coefficients
5. I don't understand statistics
6. I have little experience of computers
7. All computers hate me
8. I have never been good at mathematics
9. My friends are better at statistics than me
10. Computers are useful only for playing games
11. I did badly at mathematics at school
12. People try to tell you that SPSS makes statistics easier to understand but it
doesn't
© Shamshuritawati
4

5. Example : SAQ. (Item 3 reversed).sav
13. I worry that I will cause irreparable damage because of my incompetence with
computers
14. Computers have minds of their own and deliberately go wrong whenever I use
them
15. Computers are out to get me
16. I weep openly at the mention of central tendency
17. I slip into a coma whenever I see an equation
18. SPSS always crashes when I try to use it
19. Everybody looks at me when I use SPSS
20. I can't sleep for thoughts of eigen vectors
21. I wake up under my duvet thinking that I am trapped under a normal
distribution
22. My friends are better at SPSS than I am
23. If I'm good at statistics my friends will think I'm a nerd
© Shamshuritawati
5

6. RELIABILITY TEST
6
Click Analyze >> Scale >> Reliability Analysis
Select “all 23 items”
into Items
Click on Statistics
√ Item
√ Scale
√ Scale if item
deleted
Summaries:
√ Correlations
Click on Continue
Click OK
© Shamshuritawati

7. RELIABILITY TEST
The alpha value is high (> 0.7). Therefore the
23 items are consistent and thus reliable for
measuring student’s anxiety towards learning
SPSS.
7
© Shamshuritawati
Reliability Statistics
Cronbach's Alpha
Cronbach's Alpha
Based on
Standardized
Items N of Items
.806 .819 23

8. RELIABILITY TEST
8
© Shamshuritawati
Item-Total Statistics
Scale Mean if
Item Deleted
Scale
Variance if
Item Deleted
Corrected
Item-Total
Correlation
Squared
Multiple
Correlation
Cronbach's
Alpha if Item
Deleted
Question_01 59.89 90.121 .521 .373 .792
Question_02 60.64 101.064 -.163 .188 .820
Question_03 58.85 89.021 .435 .398 .794
Question_04 59.48 87.968 .569 .385 .788
Question_05 59.54 89.303 .481 .291 .792
Question_06 60.04 87.605 .482 .427 .791
Question_07 59.34 85.656 .594 .470 .785
Question_08 60.03 89.900 .504 .490 .792
Question_09 59.42 100.882 -.137 .220 .829
Question_10 59.99 92.233 .356 .197 .799
Question_11 60.01 88.790 .568 .530 .789
Question_12 59.11 88.452 .563 .424 .789
Question_13 59.82 87.840 .577 .451 .788
Question_14 59.39 87.492 .562 .393 .788
Question_15 59.50 88.766 .484 .344 .792
Question_16 59.39 88.329 .571 .463 .789
Question_17 59.80 88.442 .588 .494 .788
Question_18 59.70 85.993 .609 .492 .785
Question_19 59.97 104.442 -.296 .209 .832
Question_20 58.64 91.699 .314 .270 .801
Question_21 59.10 87.679 .561 .454 .788
Question_22 59.38 101.109 -.153 .167 .824
Question_23 58.83 98.821 -.044 .086 .819

9. RELIABILITY TEST
Corrected Item-Total Correlation indicate correlation between
each item and total score. Low values (<0.3) indicates the item is
measuring something different from the scale as a whole. If it is too
low, drop the item.
For these data, all data have item-total correlation above 0.3, which
is encouraging.
Cronbach Alpha if Item Deleted measures the impact of
removing each item. If the values of alpha is higher than overall
alpha, it means that the deletion of that item improve reliability.
Therefore, we may consider to drop the item.
9
© Shamshuritawati

10. RELIABILITY TEST
If Cronbach alpha is high (>0.7), just ignore the mean
for inter-item correlations.
If Cronbach alpha is low (<0.7), check the mean for
inter-item correlations and make sure the value is
>0.2. If the value is >0.2 and Cronbach alpha is <0.7,
we can still conclude that all items were reliable.
10
© Shamshuritawati
Summary Item Statistics
Mean Minimum Maximum Range
Maximum /
Minimum Variance
N of
Items
Inter-Item
Correlations
.165 -.342 .629 .971 -1.842 .060 23

11. RELIABILITY TEST
How to report?
Cronbach's alpha coefficient for all 23 items is 0.806.
Therefore, it has indicated more than 0.7 (Nunnally,
1978). All the variables are said to be reliable.
11
© Shamshuritawati

12. Factor Analysis
Presented by
Shamshuritawati Sharif
School of Quantitative Sciences
College of Arts and Sciences
12
© Shamshuritawati

13. Understanding Factor Analysis
 Factor analysis is commonly used in:
 Data reduction
 Scale development
 The evaluation of the psychometric quality of a measure, and
 The assessment of the dimensionality of a set of variables.
 Regardless of purpose, factor analysis is used in:
 the determination of a small number of factors based on a
particular number of inter-related quantitative variables.
 The scale must be at least interval. However, in
social science studies, Likert scale are often used.
13
© Shamshuritawati

14. Understanding Factor Analysis
 Unlike variables directly measured such as speed, height,
weight, etc., some variables such as egoism, creativity,
happiness, religiosity, comfort are not a single
measurable entity.
 They are constructs that are derived from the
measurement of other, directly observable variables.
 Constructs are usually defined as unobservable latent
variables. e.g.:
 motivation/love/hate/care/altruism/anxiety/worry/stress/product
quality/physical aptitude/democracy /reliability/power.
14
© Shamshuritawati

15. Understanding Factor Analysis
15
 Generally, the number of factors is much smaller than the
number of measures. Therefore, the expectation is that a
factor represents a set of measures.
 Observed correlations between variables result from their
sharing of factors. Example: Correlations between a person’s
test scores might be linked to shared factors such as general
intelligence, critical thinking and reasoning skills, reading
comprehension etc.
© Shamshuritawati

16. Understanding Factor Analysis
16
 A major goal of factor analysis is to represent
relationships among sets of variables parsimoniously
yet keeping factors meaningful.
 A good factor solution is both simple and
interpretable.
 When factors can be interpreted, new insights are
possible.
© Shamshuritawati

17. Application of Factor Analysis
17
 Defining dimensions for an existing measure:
 In this case the variables to be analyzed are chosen by the initial
researcher and not the person conducting the analysis.
 Factor analysis is performed on a predetermined set of items/scales.
 Results of factor analysis may not always be satisfactory:
 The items or scales may be poor indicators of the construct or constructs.
 There may be too few items or scales to represent each underlying dimension.
© Shamshuritawati

18. Application of Factor Analysis
18
 Selecting items or scales to be included in a measure.
 Factor analysis may be conducted to determine what items or
scales should be included and excluded from a measure.
 Results of the analysis should not be used alone in making
decisions of inclusions or exclusions. Decisions should be
taken in conjunction with the theory and what is known about
the construct(s) that the items or scales assess.
© Shamshuritawati

19. Initial Consideration
19
 Communalities
 The communalities for the ith variable are computed by taking the
sum of the squared loadings for that variable. Refer Example.
 Sample size.
o Correlation fluctuate from sample to sample, much more so in
small sample than in large. Therefore EFA also depends on sample
size.
o Collect from not < 50, preferably > 100:20 cases/variable
 Data Screening
 Look for at the intercorrelation between variables/items
 If our test questions/items measure the same underlying construct,
then we would expect them to correlate with each other because they
are measuring the same thing.
© Shamshuritawati

20. Example : Communalities
20
© Shamshuritawati

21. Steps in Factor Analysis
21
 Factor analysis usually proceeds in four steps:
 1st
Step: Correlation matrix for all variables is computed
 2nd
Step: Factor extraction
 3rd
Step: Factor rotation
 4th
Step: Make final decisions about the number of underlying
factors
© Shamshuritawati

22. Steps in Factor Analysis:
The Correlation Matrix
22
 1st
Step: the correlation matrix
 Generate a correlation matrix for all variables
 Identify variables not related to other variables
 If the correlation between variables are small, it is unlikely that
they share common factors (variables must be related to each
other for the factor model to be appropriate).
 Think of correlations in absolute value.
 Correlation coefficients greater than 0.3 in absolute value are
indicative of acceptable correlations.
 Examine visually the appropriateness of the factor model.
© Shamshuritawati

23. Steps in Factor Analysis:
The Correlation Matrix
Inter-correlation
Correlation matrix : scanning p-value < 0.05,
Correlation matrix: look for multicollinearity (variables highly
correlated – R>0.9) and singularity (perfectly correlated)
Determinant: >0.00001 (no multicollinearity)
Anti-image correlation matrix
Assess sampling adequacy of each variable
MSA<0.5 is inadequate: exclude the variable
Look at the diagonal element of anti-image correlation matrix if KMO
is not OK!
Department of Statistics
Ida Rosmini Othman
23

24. Steps in Factor Analysis:
The Correlation Matrix
 Bartlett Test of Sphericity:
 used to test the hypothesis the correlation matrix is an identity
matrix (all diagonal terms are 1 and all off-diagonal terms are 0).
 If the value of the test statistic for sphericity is large and the
associated significance level is small, it is unlikely that the
population correlation matrix is an identity.
 scanning p-value < 0.05, if so – OK!
24
© Shamshuritawati

25. Steps in Factor Analysis:
The Correlation Matrix
 The Kaiser-Meyer-Olkin (KMO) measure of
sampling adequacy:
 Measure degree of inter-correlation among variables
 The closer the KMO measure to 1 indicate a sizeable sampling
adequacy (> 0.9 is superb, 0.8 and higher are great, 0.7 is
acceptable, 0.6 is mediocre, less than 0.5 is unacceptable ).
 Range from 0.5 to 1 – Minimum 0.5-OK!
 Reasonably large values are needed for a good factor analysis.
Small KMO values indicate that a factor analysis of the variables
may not be a good idea.
 Look at the diagonal element of anti-image correlation matrix if
KMO is not OK!
25
© Shamshuritawati

26. Steps in Factor Analysis:
Factor Extraction
26
 2nd
Step: Factor extraction
 The primary objective of this stage is to determine the factors.
 Initial decisions can be made here about the number of factors underlying
a set of measured variables.
 Estimates of initial factors are obtained using Principal components
analysis.
 The principal components analysis is the most commonly used extraction
method . Other factor extraction methods include:
 Maximum likelihood method
 Principal axis factoring
 Alpha method
 Unweighted lease squares method
 Generalized least square method
 Image factoring.
© Shamshuritawati

27. Steps in Factor Analysis:
Factor Extraction
27
 In principal components analysis, linear combinations of the
observed variables are formed.
 The 1st
principal component is the combination that accounts for the
largest amount of variance in the sample (1st
extracted factor).
 The 2nd
principle component accounts for the next largest amount of
variance and is uncorrelated with the first (2nd
extracted factor).
 Successive components explain progressively smaller portions of the
total sample variance, and all are uncorrelated with each other.
© Shamshuritawati

28. Steps in Factor Analysis:
Factor Extraction
28
 To decide on how many factors we
need to represent the data, we use 2
statistical criteria:
 Eigen Values, and
 The Scree Plot.
 The determination of the number of
factors is usually done by considering
only factors with Eigen values greater
than 1.
 Factors with a variance less than 1 are
no better than a single variable, since
each variable is expected to have a
variance of 1.
Total Variance Explained
Comp
onent
Initial Eigenvalues
Extraction Sums of Squared
Loadings
Total
% of
Variance
Cumulativ
e % Total
% of
Variance
Cumulativ
e %
1 3.046 30.465 30.465 3.046 30.465 30.465
2 1.801 18.011 48.476 1.801 18.011 48.476
3 1.009 10.091 58.566 1.009 10.091 58.566
4 .934 9.336 67.902
5 .840 8.404 76.307
6 .711 7.107 83.414
7 .574 5.737 89.151
8 .440 4.396 93.547
9 .337 3.368 96.915
10 .308 3.085 100.000
Extraction Method: Principal Component Analysis.
© Shamshuritawati

29. Steps in Factor Analysis:
Factor Extraction
 The examination of the Scree plot
provides a visual of the total variance
associated with each factor.
 The steep slope shows the large
factors. The gradual trailing off (scree)
shows the rest of the factors usually
lower than an eigen value of 1.
 In choosing the number of factors, in
addition to the statistical criteria, one
should make initial decisions based on
conceptual and theoretical grounds.
29
© Shamshuritawati
 At this stage, the decision
about the number of factors is
not final.

30. Steps in Factor Analysis:
Factor Extraction
Kaiser’s criterion
Retain factors with eigen values > 1
Scree plot
use point of inflexion (find point at which the shape of the curves
changes direction and becomes horizontal)
retain factors above elbow
Parallel Analysis
Compare the eigenvalues from FA and simulation using Monte Carlo
30

31. Steps in Factor Analysis:
Factor Extraction
Which Rule?
 Use Kaiser’s criterion when
 less than 30 variables & communalities after extraction>0.7
 sample size>250 and mean communality>0.6
 Use Scree plot
 sample size>250
 Use Parallel Analysis to get accurate result and
recommended by many journals
31

32. Steps in Factor Analysis:
Factor Rotation
32
 3rd
Step: Factor rotation.
 In this step, factors are rotated.
 Un-rotated factors are typically not very interpretable (most
factors are correlated with may variables).
 Factors are rotated to make them more meaningful and easier
to interpret (each variable is associated with a minimal
number of factors).
 Different rotation methods may result in the identification of
somewhat different factors.
© Shamshuritawati

33. Steps in Factor Analysis:
Factor Rotation
 The most popular rotational method is Varimax
rotations.
 Varimax use orthogonal rotations yielding uncorrelated
factors/components.
 Varimax attempts to minimize the number of variables that
have high loadings on a factor. This enhances the
interpretability of the factors.
33
© Shamshuritawati

34. Steps in Factor Analysis:
Factor Rotation
 Other common rotational method used include Oblique
rotations which yield correlated factors.
 Oblique rotations are less frequently used because their
results are more difficult to summarize.
 Other rotational methods include:
 Quartimax (Orthogonal)
 Equamax (Orthogonal)
 Promax (oblique)
34
© Shamshuritawati

35. Steps in Factor Analysis:
Making Final Decisions
35
 4th
Step: Making final decisions
 The final decision about the number of factors to choose is the number of
factors for the rotated solution that is most interpretable.
 To identify factors, group variables that have large loadings for the same
factor.
 Plots of loadings provide a visual for variable clusters.
 Interpret factors according to the meaning of the variables
 This decision should be guided by:
 A priori conceptual beliefs about the number of factors from past research or
theory
 Eigen values computed in step 2.
 The relative interpretability of rotated solutions computed in step 3.
© Shamshuritawati

36. Assumptions Underlying Factor Analysis
36
 Assumption underlying factor analysis include.
 The measured variables are linearly related to the factors + errors.
 This assumption is likely to be violated if items limited response scales
(two-point response scale like True/False, Right/Wrong items).
 The data should have a bivariate normal distribution for each pair of
variables.
 Observations are independent.
 The factor analysis model assumes that variables are determined by
common factors and unique factors. All unique factors are assumed
to be uncorrelated with each other and with the common factors.
© Shamshuritawati

37. Checklist
37
 Based on results.
 Correlation : scan for p-value > 0.05, too high coefficient
 Determinant > 0.00001 – OK!
 KMO > 0.5 and above- OK! , if not check anti-image correlation
 Bartlett’s test, p-value < 0.05 – OK!
 How many factors?
 Refer Communalities and extraction (all values > 0.7)
 Total variance explained (Scree plot)
© Shamshuritawati

38. Factor Analysis via SPSS
Presented by
Shamshuritawati Sharif
School of Quantitative Sciences
College of Arts and Sciences
38
© Shamshuritawati

39. Analyze >> Data Reduction >> Factor
39
2
2
1
1
3
3
4
4

40. Example : SAQ. (Item 3 reversed).sav
Fear of computers
6. I have little experience of computers
7. All computers hate me
10. Computers are useful only for playing games
13. I worry that I will cause irreparable damage because of my incompetence with computers
14. Computers are out to get me
15. I weep openly at the mention of central tendency
16. SPSS always crashes when I try to use it
18. I can't sleep for thoughts of eigen vectors
Fear of mathematics
8. I have never been good at mathematics
11. I did badly at mathematics at school
17. I slip into a coma whenever I see an equation
© Shamshuritawati
40

41. Example : SAQ. (Item 3 reversed).sav
Fear of statistics
1. Statistics makes me cry
3. Standard deviations excite me
4. I dream that Pearson is attacking me with correlation coefficients
5. I don't understand statistics
12. People try to tell you that SPSS makes statistics easier to understand but it doesn't
14. Computers have minds of their own and deliberately go wrong whenever I use them
21. I wake up under my duvet thinking that I am trapped under a normal distribution
Fear of peer evaluation
2. My friends will think I'm stupid for not being able to cope with SPSS
9. My friends are better at statistics than me
19. Everybody looks at me when I use SPSS
20. My friends are better at SPSS than I am
21. If I'm good at statistics my friends will think I'm a nerd
© Shamshuritawati
41

42. FACTOR ANALYSIS
How to report ?:
A factor analysis was initially conducted on 23 items with
varimax rotation(direct oblimin). However, three
items were removed due to cross-loadings. The final model
consist of 23 items. The Kaiser-Meyer-Olkin measure verified
the sampling adequacy for the analysis, KMO =0 .93 (‘great’
according to Field, 2009), and all MSA values for individual
items were larger than 0 .80, which is well above the
acceptable limit of 0.50 (Field, 2009). Bartlett’s test of
sphericity 2
(253) = 19334.49, p-value < 0.05, indicated
that correlations between items are sufficiently large for
Factor analysis.
42

43. FACTOR ANALYSIS
How to report (cont.)?
Four factors had eigenvalues over Kaiser’s criterion of 1 and
explained 50.3% of the variance. The scree plot supported the
Kaiser’s criterion in retaining four factors. Given the large
sample size, and convergence of the scree plot and Kaiser’s
criterion on four factors, this is the number of factors that
were retained in the final analysis. Table 1 shows the factor
loadings. The items that cluster on the same factors suggest
that factor 1 represent fear of computer, factor 2
represent fear of mathematics, factor 3 represent fear
of statistics and factor 4 represent fear of peer
evaluations.
43

44. Table 1: Summary of exploratory factor analysis result for xxx
questionnaire (N = xxx)
44
Factor Loading
Factor 1 Factor 2 Factor 3 Factor 4
Item 1
Item 2
.
.
Item n
Eigenvalue
% of variance
Cronbach 

45. References
 J. C. Nunnally, Psychometric Theory (2nd ed.). New York: McGraw-
Hill, 1978
 Cortina, J. M. (1993). What is coefficient alpha? An examination of
theory and applications. Journal of Applied Psychology,78, 98-104.
 Andy Field
 Data : http://www.sagepub.com/field3e/Aboutthebook.htm
 Julie Pallant
 http://www.academia.dk/BiologiskAntropologi/Epidemiologi/PDF/
SPSS_Survival_Manual_Ver15.pdf
 http://www.allenandunwin.com/spss/datafiles.html
© Shamshuritawati
45

46. Formula
© Shamshuritawati
46

47. FACTOR ANALYSIS
Factor Loadings (Cutoff point at 99% level) – Andy
Field
47
Factor Loading Sample Size Needed
0.722 50
0.512 100
0.364 200
0.298 300
0.21 600
0.162 1000

48. FACTOR ANALYSIS
Factor Loadings (Cutoff point at 95% level) – Hair et al
48
Factor Loading Sample Size Needed
.75 50
.70 60
.65 70
.60 85
.55 100
.50 120
.45 150
.40 200
.35 250
.30 350

49. CFA : Model Fit
Fit Indices Authors
Recommended
Value
Current
Fit Indices
CMIN Tabachink & Fidell (1996) Reported: If n
between 100–200
2.496
p-value > 0.05
CMIN/df Marsh & Hocevar (1985);
Bentler (1990)
< 5.0
< 5.0
Reported: If
n > 200
2.496
RMSEA Byrne (2001);
Hu & Bentler (1999)
< 0.08
< 0.05
0.089
GFI Chau (1997) ; Segars & Grover (1993) >0.90 0.991
CFI Bentler (1990) ; Hatcher (1994) > 0.90 0.990
NFI Bentler & Bonett (1980) > 0.90 0.984
TLI Kenny D.A (2003) > 0.90
© Shamshuritawati
49