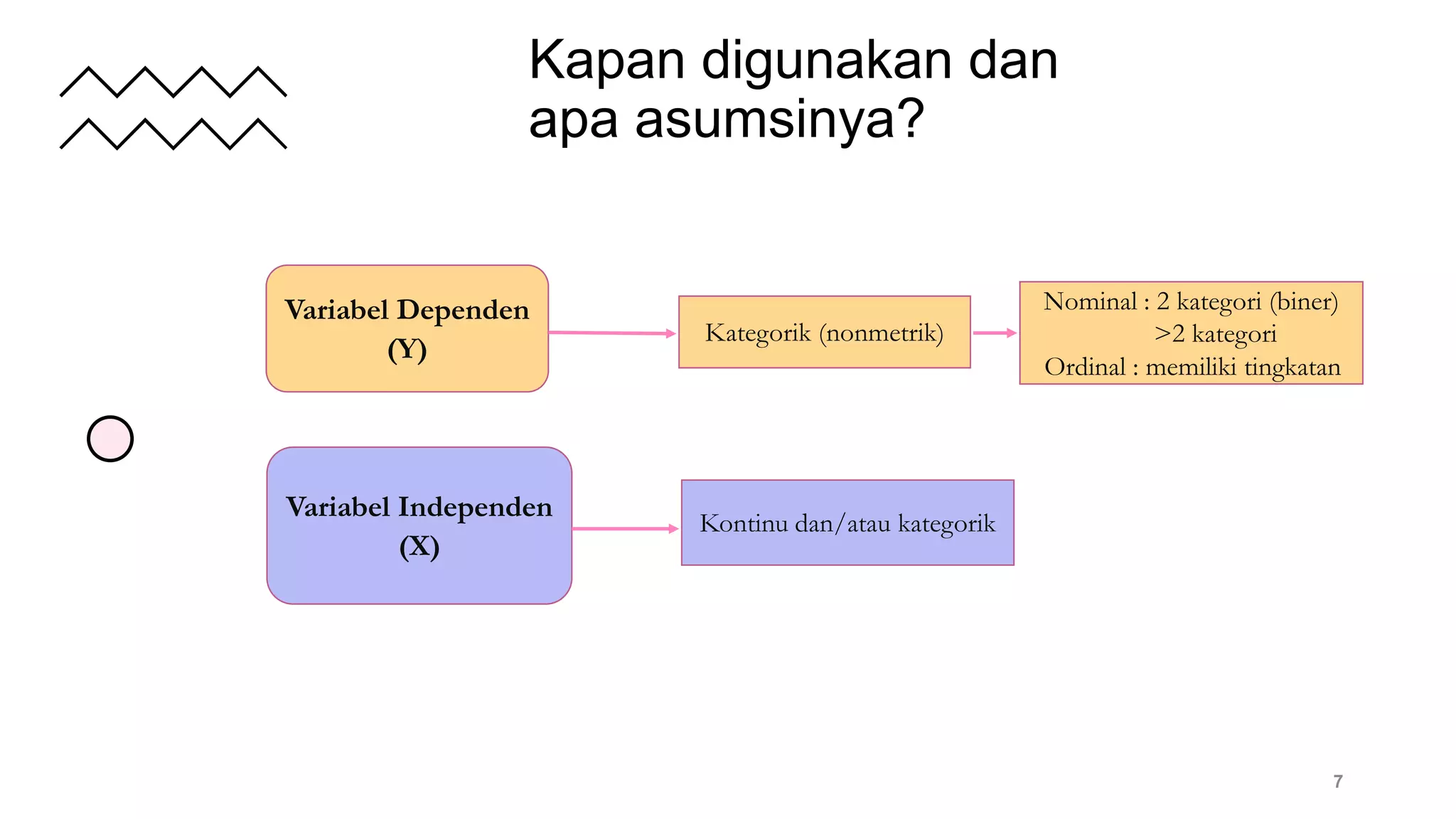
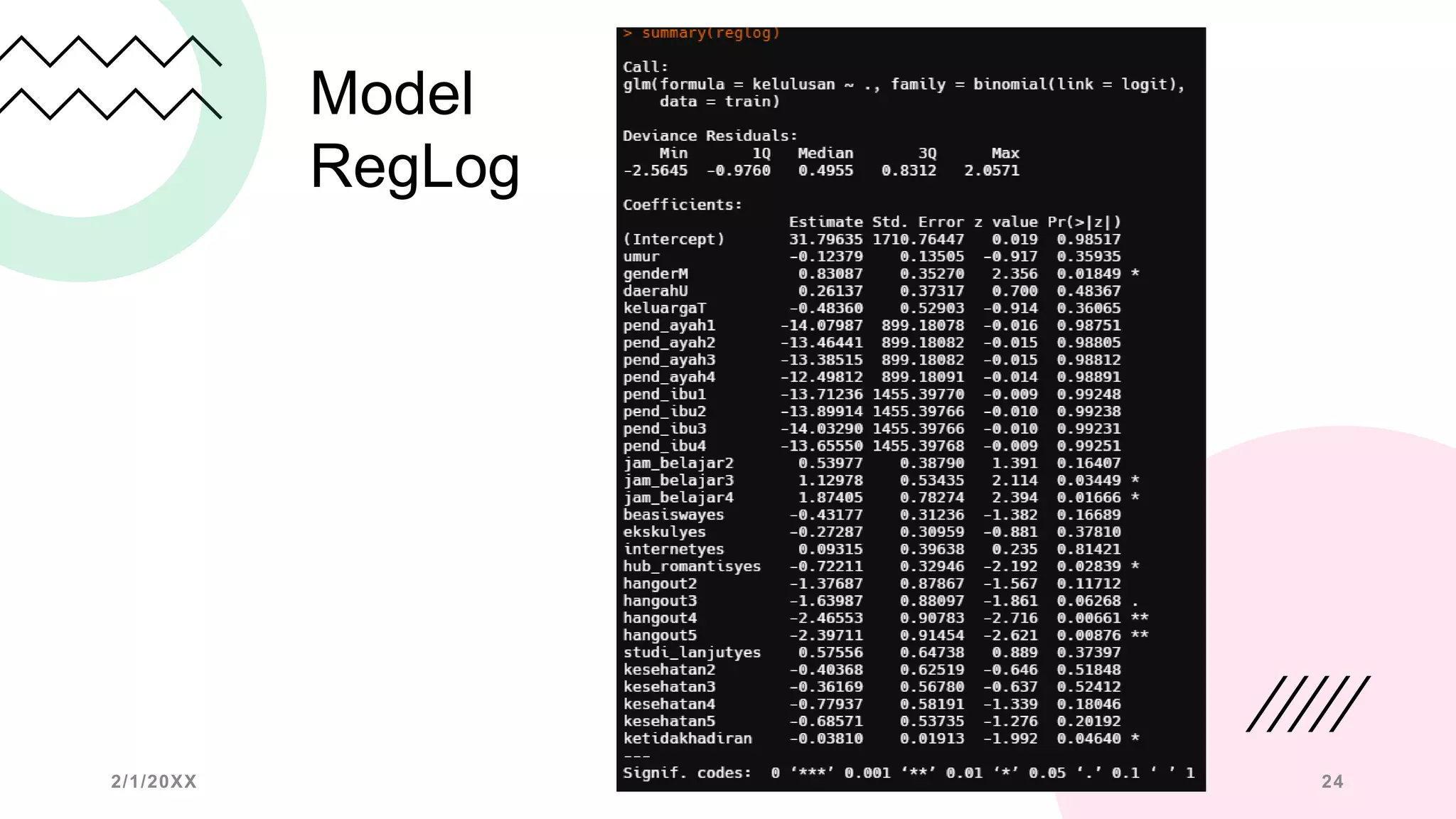
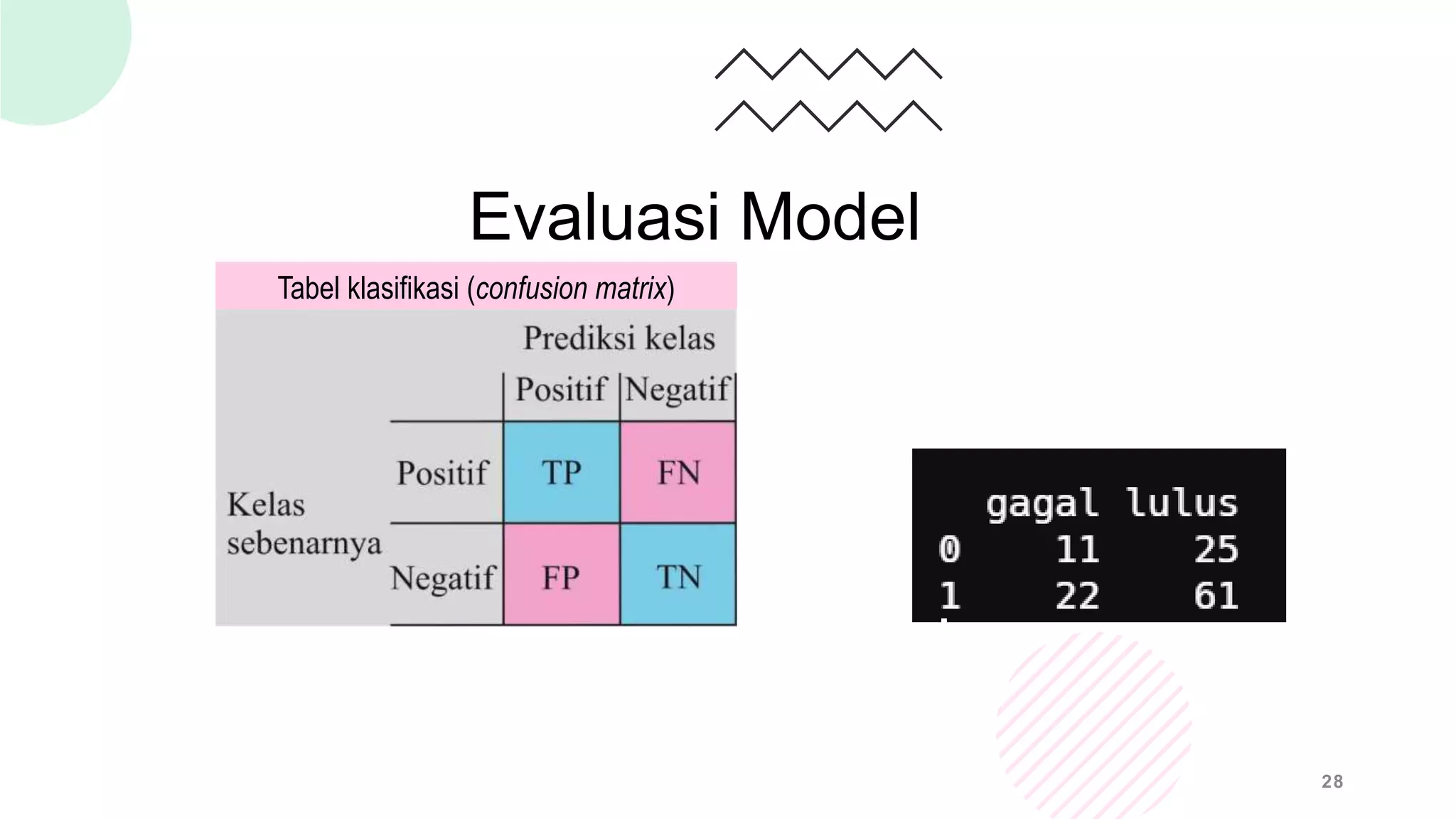
Dokumen ini membahas regresi logistik sebagai metode analisis statistik untuk hubungan antara variabel dependen kategorik dan variabel independen. Ini mencakup konsep dasar, asumsi, model, dan teknik evaluasi seperti goodness of fit, serta penyusunan dan validasi model. Selain itu, terdapat contoh penggunaan regresi logistik dengan data penyakit jantung, termasuk analisis faktor dan perhitungan peluang.

1. REGRESI
LOGISTIK ANDI HARPENI DEWANTARA
YESSICA MEGA APRITA
STATISTIKA MULTIVARIAT
S3 PEP UNY 2022

2. OUTLINE
17/10/2022 REGRESI LOGISTIK 2
Konsep Dasar (Definisi, Asumsi, Tujuan)
Model Persamaan
Pendugaan Parameter
Hipotesis dan Statistik Uji
Penyusunan dan Validasi Model
Goodness of Fit
Contoh Kasus
Simulasi dengan R-Studio

3. Kenapa menggunakan
regresi logistik?
3

4. Analisis Regresi
4
Analisis yang digunakan untuk
menganalisis hubungan antara
satu atau beberapa variabel
independen dengan sebuah
variabel dependen.

5. 5
Model
Regresi
Linear
Regresi
Linear
Sederhana
Regresi Linear
Berganda
Non-Linear
Regresi Logistik
Regresi
Logistik
Biner
Regresi
Logistik
Multinomial
Regresi
Logistik
Ordinal

6. Definisi
6
Regresi logistik merupakan suatu metode analisis
statistik untuk menggambarkan hubungan antara
peubah respon/ variabel dependen yang bersifat
kategorik dengan satu atau lebih variabel independen
dalam skala kontinu dan/atau kategorik.

7. Kapan digunakan dan
apa asumsinya?
7
Nominal : 2 kategori (biner)
>2 kategori
Ordinal : memiliki tingkatan
Kontinu dan/atau kategorik
Variabel Independen
(X)
Variabel Dependen
(Y)
Kategorik (nonmetrik)

8. 8
REGRESI LOGISTIK
Var. Independen (X)
Var. Dependen
(Y)
Tidak Linier
Metode OLS
Pelanggaran Asumsi • Error tidak normal
• Ragam tidak homogen
• Nilai dugaan Y melebihi rentang 0-1

9. 9
Sumber: Slide Presentasi Analisis Diskriminan (Diniaty & Normalia, 2022)

10. Kapan digunakan dan
apa asumsinya?
10
1. Variabel dependen harus bersifat kategorikal.
2. Tidak ada korelasi yang signifikan antarvariabel independen.
3. Linearitas dalam format logit. Hubungan antara logit
dependen variable dengan variabel independen harus linear.
4. Jumlah observasi untuk setiap variabel harus memadai dan
jumlah sampel secara keseluruhan cukup besar.

11. 1. Mengetahui faktor-faktor variabel independen yang
mempengaruhi variabel dependen
2. Menghitung peluang (persamaan yang diperoleh dari
proses regresi logistik dapat digunakan untuk menghitung
peluang seseorang di luar responden yang termasuk dalam
penelitian).
3. Melihat perbedaan karakteristik antara 2 kelompok, untuk
membahas karakteristik ini biasanya membahas nilai odds
ratio di masing-masing variabel bebas
TUJUAN
11

12. 12
Sampel Gender AGRP Usia CHD
1 1 1 20 0
2 0 1 23 0
3 1 1 24 0
4 1 1 25 0
5 1 1 25 1
6 0 1 26 0
7 0 1 26 0
8 0 1 28 0
9 1 1 28 0
10 0 1 29 0
11 1 2 30 0
12 1 2 30 0
Sampel Gender AGRP Usia CHD
51 1 4 44 1
52 0 4 44 1
53 1 5 45 0
54 1 5 45 1
55 1 5 46 0
56 0 5 46 1
57 0 5 47 0
58 0 5 47 0
59 1 5 47 1
60 0 5 48 0
61 1 5 48 1
62 1 5 48 1
Ilustrasi Data
Berikut data 100 orang dengan informasi jenis kelamin dan apakah terdapat tanda
gangguan penyakit jantung (CHD) atau tidak (Sumber: Hosmer & Lemeshow (2000).

13. 13
negatif
>1
Prediksi bisa tidak sesuai
Usia
Positif
Y=1
Negatif
Y=0
Positif
Y=1
Negatif
Y=0
Usia
Model Regresi linear tidak cocok digunakan

14. 14
Age Group n CHD Proportion
Ada (1) Tidak Ada (0)
20-29 10 9 1 0.10
30-34 15 13 2 0.13
35-39 12 9 3 0.25
40-44 15 10 5 0.33
45-49 13 7 6 0.46
50-54 8 3 5 0.63
55-59 17 4 13 0.766
60-69 10 2 8 0.80
Total 100 57 43 0.43

15. 15
P(Positif)
P(Y=1)
P(Negatif)
P(Y=0) X
Positif
Y=1
Negatif
Y=0 X
Proporsi
𝑃(𝑌 = 1) =
𝑒𝛽0+𝛽1𝑋1
1 + 𝑒𝛽0+𝛽1𝑋1
𝑙𝑜𝑔
𝑝
1 − 𝑝
= 𝛽0 + 𝛽1𝑋1
Konsep Dasar

16. 16
𝑃(𝑌 = 1) =
𝑒𝛽0+𝛽1𝑋1
1 + 𝑒𝛽0+𝛽1𝑋1
𝑙𝑜𝑔
𝑝
1 − 𝑝
= 𝛽0 + 𝛽1𝑋1
Model Persamaan Regresi
Logistik
Jika terdapat p variabel, maka secara umum dapat dituliskan sebagai berikut:
𝑃(𝑌 = 1) =
𝑒𝛽0+𝛽1𝑋1+𝛽2𝑋2+⋯+𝛽𝑝𝑋𝑝
1 + 𝑒𝛽0+𝛽1𝑋1+𝛽2𝑋2+⋯+𝛽𝑝𝑋𝑝

17. Pendugaan Parameter
17
Fungsi likelihood
• Untuk mengestimasi parameter β dalam model logit tidak dapat digunakan metode least square seperti
pada model regresi linear.
• Digunakan metode maximum likelihood.
• Akan dicari nilai β yang akan memaksimalkan fungsi likelihood.

18. Pendugaan Parameter
18
Fungsi likelihood
Fungsi log-likelihood

19. 19
Hipotesis
Uji simultan
H0: 𝛽1 = 𝛽2 = … = 𝛽p = 0, tidak ada variabel yang berpengaruh
H1: 𝛽1 ≠ 𝛽2 ≠ … ≠ 𝛽p ≠ 0, minimal ada 1 variabel yang berpengaruh
Uji Parsial
H0: 𝛽j = 0, variabel ke-j tidak berpengaruh
H1: 𝛽j ≠ 0, variabel ke-j berpengaruh

20. 20
Pengujian signifikasi
parameter model logit
Menggunakan argumentasi yang mirip pada analisis regresi linear: “Apakah model dengan variable
independen yang diuji memberikan informasi lebih bayak tentang variable dependen dibandingkan dengan
model yang tanpa variabel independent tersebut”.
Melakukan perbandingan dengan menggunakan statistik deviance

21. 21
Statistik Uji
Uji Simultan
Uji Parsial
Statistik G
Uji Wald
Deviance

22. 22
Goodness of
Fit
Model
evaluasi
training:uji =
80:20
70:30
Data training
Data testing
Performa model
(Good/Bad)

23. evaluasi
23
Data training & Data testing
Model
training:testing
= 70:30
Data training
Data testing
Performa model
(well/not)

24. 2/1/20XX PRESENTATION TITLE 24
Model
RegLog

25. PRESENTATION TITLE 25
Uji
Simultan &
Uji Parsial

26. 26
Goodness of Fit

27. 27
Evaluasi Model
Membandingkan Y aktual dari
data testing dengan Ŷ (Y
prediksi) model RegLog

28. 28
Evaluasi Model
Tabel klasifikasi (confusion matrix)

29. 29

30. T H A N K
Y O U
30