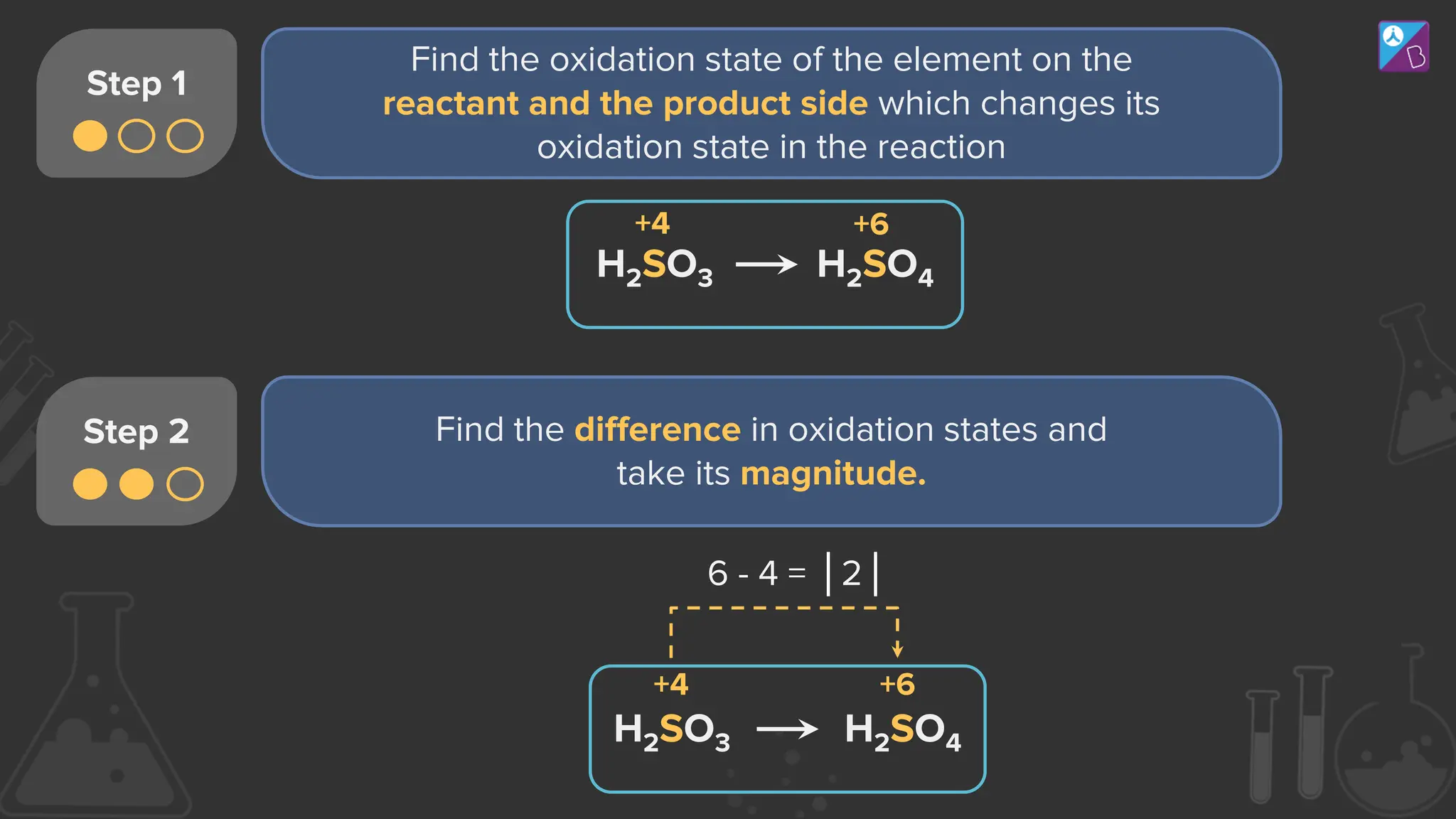
The document discusses redox reactions, detailing the concepts of oxidation and reduction, including changes in oxidation numbers and their significance in chemical reactions. It outlines rules for determining oxidation states, provides examples of various redox reactions, and explains methods for balancing these reactions in both acidic and basic media. Additionally, it introduces the concept of equivalent mass and normality in relation to redox titration, emphasizing the importance of identifying oxidizing and reducing agents.



















































![MnO4
− (aq) + 5Fe2+ (aq) + 8H+ (aq) Mn2+ (aq)+ 5Fe3+ (aq) + 4H2O (l)
Charge on the reactant side
= [ 1 × (−1) + 5 × (+2) + 8 × (+1) ] = +17
Charge on the product side
= [1 × (+2) + 5 × (+3) + 4 × (0)] = +17
For an Acidic Medium](https://image.slidesharecdn.com/redoxreactionsstoichiometryvolumetricanalysis-241211114311-9c8ebbb4/75/Redox-Reactions-Stoichiometry-Volumetric-Analysis-pdf-53-2048.jpg)






















































