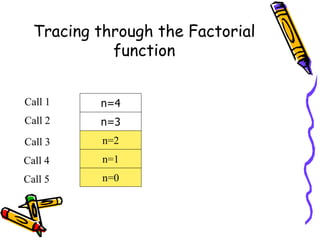
This document discusses recursion, including: - Recursive functions call themselves, with a base case to end recursion and a general case that calls a smaller version. - Recursive solutions are generally less efficient than iterative ones but work for some problems. - Examples include computing powers and factorials recursively, and solving the Towers of Hanoi puzzle recursively by breaking it into smaller subproblems.

2. Recursion

3. Recursion
You should be able to identify the base
case(s) and the general case in a
recursive definition
• To be able to write a recursive
algorithm for a problem involving only
simple variables.

4. A Recursive call
• A function call in which the function being
called is the same as the one making the
call.
• Put differently it is a function call to
itself.
• When a function calls itself this is said to
be a recursive call.
• The word recursive means: having the
characteristics of coming up again or
repeating.
• Can be used instead of iteration or looping

5. Efficiency considerations
• Recursive solutions are generally less
efficient than iterative solutions.
• Some problems that we will see lend
themselves to recursion
• Some languages do not allow recursion e.g.
Fortran, Basic and Cobol
• Lisp on the other hand is especially suited
for recursive algorithms
• Initially we will look at recursive algorithms
on simple variables we will then look at
recursion on structured data

6. What is recursion?
• The simplest use of the recursive
algorithm is to compute a number
raised to a given power, e.g. 2^3 is
2x2x2, 4^5 is 4x4x4x4x4 and so on.
• y^n, yxyxyxyxyxyx…. (n times)
• y^n is yxy^(n-1)
• y^n is yxyxy^(n-2)
• etc

7. The recursive definition
• This is the important bit.
• We can write x^n as x * x^(n-1). Hence
something is defined in terms of a smaller
version of itself
• Base case: the case for which the solution
can be stated non recursively
• General case: the case for which the
solution is expressed in terms of a smaller
version of itself

8. See program power.cpp
demo
• Run power.cpp
• See also power*.cpp in the cpteach directory included in
the week 8 directory
• See all Visual Basic illustrations in this directory go t
examples directory

9. Some comments on the
program
• Each recursive call to Power can be
thought of as creating its own copy of
the parameters x and n.
• x remains the same for each call but
the value of n decreases each time.
• Lets consider the case with number
=2 and exponent = 3, so we are
computing 2^3 which is 8

10. Tracing through the Power
program
•Call 1. Power is called by main, with number
equal to 2 and exponent equal to 3.
•Because n does not equal 1 Power is called
recursively with x and n-1as arguments.
•Call 2: x is equal to 2 and n is equal to 2.
Because n does not equal 1 the function Power is
called recursively.
•Call 3: x = 2 and n = 1. As n=1, the value of x is
returned. This call to the function has terminated

11. Infinite recursion
• If the function Power was called with n
negative then the condition n==1 would
never be satisfied since starting at a value
less than zero and continually subtracting
1 would mean that a value of 1 is never
obtained.
• I have altered this now so that negative
powers are calculated

12. Execution of Power(2,3)
X=2, n=1
X=2, n=2
X=2, n=3
Call 3
Call 2
Call 1
Power(2,3)

13. Recursive algorithms with
Simple Variables
• Lets look at a special mathematical
function important in so many areas
of mathematics. It is the factorial
function defined as
• n! = nx(n-1)x(n-2)x……1
• E.g. 4! = 4*3*2*1 = 24

14. Run Factorial demo
Factorial.cpp

15. Tracing through the Factorial
function
n=0
n=1
n=2
n=3
n=4
Call 5
Call 4
Call 3
Call 2
Call 1

16. Iterative solution
Writing the code without using recursion gives:
int Factorial(int n)
{
int factor;
int count;
Factor = 1;
for (count=2;count<=n;count++)
Factor=Factor*count;
return Factor;
}

17. The Towers of Hanoi
• Very old problem demonstrating
recursion.
• Only one disc can be moved at a time
• After each move, all discs must be on
the poles
• No disc may be placed on top of a
disc which is smaller than itself

18. Hanoi.cpp
• Discuss Hanoi.cpp and demonstrate