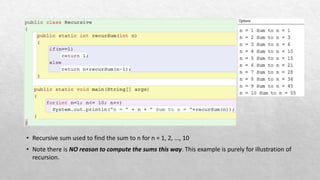
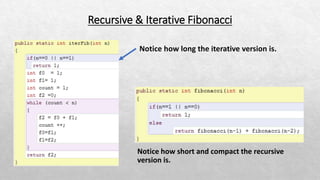
The document explains the concept of recursion in mathematics, highlighting its essential characteristics such as a base case and recursive case. It provides examples of recursive solutions for summing numbers, calculating factorials, and generating Fibonacci numbers, along with comparisons to iterative solutions. Additionally, it discusses the simplicity and coding efficiency of recursive solutions, noting that while they can be easier to implement, iterative solutions may perform better in terms of speed.

1. Recursion

2. Recursion
• In mathematics, we often say that a recursive solution is a solution such that f(xk) depends on
some of f(xk-1), f(xk-2),...f(x1), and f(x0)
• A usable recursive solution usually has the following characteristics
• –A base case. This is one which is easily calculated. It also prevents infinite loops!
• –A recursive case. This is the case in which the function “calls itself” in order to reduce the
calculations to the base case.

3. Simple problems solved recursively
• In math class we learned that 1+2+3+...+n = n*(n+1)/2
• For example, 1+2+...+10 = 10*11/2 = 55
• It is also easy to find the sum iteratively by an O(n) algorithm
int sum=0;
for i = 1 to n
sum=sum + i
• We can also solve this problem by recursion.

4. • Recursion to find 1 + 2 + + … + n
public sum(n)
if n == 1, sum =1
if n > 1, sum = n +sum(n-1)
Identify the base case
Identify the recursive case
• Example: sum(5) = 5 + sum(4)
= 5+4+sum(3) =9 +sum(3)
=9 +3+sum(2)
= 12 = 12 = 14 = 14
+sum(2)= +2+sum(1)
• On the next slide, we implement the recursive function in Java

5. • Recursive sum used to find the sum to n for n = 1, 2, ..., 10
• Note there is NO reason to compute the sums this way. This example is purely for illustration of
recursion.

6. n!
• From math class, we know that n! = n*(n-1)*(n-2)*...*3*2*1
3! = 3*2*1 = 6
5!= 5*4*3 *2 *1
• It is easy to compute n! iteratively
int prod = 1;
for i=2 to n
prod = prod * i

7. Recursive n!
• We easily observe that there is a recursive definition of n!
n! = n*(n-1) !
• For example 4 ! = 4*3*2*1 = 4*(3*2*1) = 4 * 3!
• This prompts the following function
int nfact (int n)
if n == 0 or n ==1
return 1
else
return n * nfact (n-1)

8. Fibonacci Numbers
• The Fibonacci number sequence:
1, 1, 2, 3, 5, 8, 13, ....
• The first two elements of the sequence are both 1
• Subsequent elements are formed by adding the two before it.
• Recursive Fibonacci
fib (n)
if (n==1 or n==0)
return 1;
else
return fib (n-1) + fib (n-2)

9. Recursive & Iterative Fibonacci
Notice how short and compact the recursive
version is.

10. Remarks about recursion
• In general
• A recursive solution is simpler to code than an iterative solution
• Some problems are so difficult that recursion may be the best solution
• Iterative solutions are often faster than recursive solutions

11. Recursive search
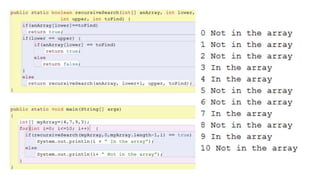
• It is very simple to write an iterative search to determine if a given value (toFind) is in an array
for i = 0 to the array length -1
if array[i] = to_find
return true
End i loop
Return false
• When we do it recursively
• If the array has length 1, we return true if the single element and toFind are the same
• If not
• we check the first element and return true if it and toFind are equal
• Otherwise, we repeat the search on the remainder of the array