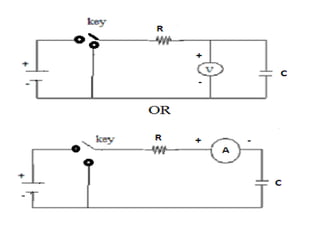
The document summarizes the aim, theory, procedure, and observations of an experiment to study the decay of charge in an RC circuit and determine the RC time constant. The key points are: 1) The experiment aims to study how the charge in a capacitor decays over time when connected to a resistor in a circuit, and determine the RC time constant. 2) Theoretically, the charge decays exponentially over time according to the equation Q(t) = Q0(1-e-t/RC). The time constant RC is the time taken for the charge to reduce to 36.8% of the initial value. 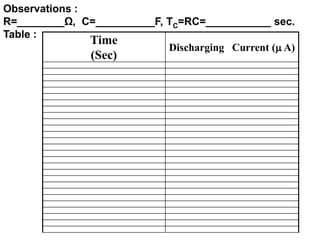3) The procedure involves charging a capacitor through a resistor, measuring

1. RC Circuit –Time constant

2. RC Circuit – Time constant
Aim: To study decay of charge in an RC circuit and
determine RC time constant
Apparatus: Board Consisting of DC Power supply, switch,
Ammeter/ Voltmeter, combinations of Resistors and
Capacitors, stop clock and connecting wires.
Theory: When a condenser ‘C’ is charged through
resistance ‘R’ then charge increases with time
exponentially and is given by the equation,
Q(t) = Q0 (1-e-t/RC).
At t = RC (seconds), then Q = 0.632 Q0.
Where Q0 is the maximum charge.

3. The product ‘CR’ is called time constant. It is equal to the
time taken to establish 0.632 times or 63% part of the final
charge Qo
Q = Qo e-t/RC.
The time constant in this case is equal to the time taken for
the charge to get reduced to 1/e part of the maximum
charge. It is equal to the time taken to discharge to a value of
0.368 part or 36% of
the maximum charge. (Q0/e =0.368 Q0).
We know I = dq/dt,
I = I0 e–t/RC (amps).
When Tc = RC, I = 0.368 I0.
Where C= capacitance in farads, R = resistance in ohms, I =
current in amperes.

4. Procedure:
1. The circuit is connected as shown in figure choosing
one set of Rand C values.
2. The capacitor C is charged for a short time by pushing
the charging switch up, till the deflection in the
ammeter is maximum but within the scale. The tap key
is then pushed down. The capacitor now starts getting
discharged through the resistor R. The stop clock is
started and readings of the ammeter are noted at an
interval of five seconds.
3. The experiment is repeated for the other values of R
and C.
4. The observations are tabulated.

6. Observations :
R=________Ω, C=__________F, TC=RC=___________ sec.
Table :
Time
(Sec)
Discharging Current ( A)

8. R(ohm) C(farad)
Tc (Experimental OR graphical
Value)
Tc (Theoretical including
error)
sec sec
Result:

9. End of the Experiment