Rama Ch6

Chöông trình Giaûng daïy Kinh teá Fulbright Phöông phaùp phaân tích Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Nieân khoùa 2003-2004 Baøi ñoïc Chöông 6: Löïa choïn daïng haøm soá vaø kieåm
ñònh ñaëc tröng moâ hình

CHÖÔNG 6

Löïa Choïn Daïng Haøm Soá vaø
Kieåm Ñònh Ñaëc Tröng Moâ Hình
Trong Chöông 4 vaø 5 chuùng ta ñaõ nghieân cöùu söï hoài qui boäi trong ñoù bieán phuï thuoäc ñang quan
taâm (Y) quan heä vôùi nhieàu bieán ñoäc laäp (Xs). Söï löïa choïn caùc bieán ñoäc laäp seõ döïa theo lyù thuyeát
kinh teá, tröïc giaùc, kinh nghieäm quaù khöù, vaø nhöõng nghieân cöùu khaùc. Ñeå traùnh söï thieân leäch cuûa
bieán bò loaïi boû nhö ñaõ thaûo luaän tröôùc ñaây; nhaø nghieân cöùu thöôøng theâm vaøi bieán giaûi thích maø
ngôø raèng coù aûnh höôûng ñeán bieán phuï thuoäc. Tuy nhieân; moái quan heä giöõa Y vaø caùc bieán X
nghieân cöùu cho ñeán giôø vaãn giaû söû laø tuyeán tính. Ñaây hieån nhieân laø raøng buoäc nghieâm ngaët vaø
khoâng thöïc teá treân moät moâ hình. Trong öùng duïng Phaàn 3.11, chuùng ta löu yù raèng bieåu ñoà phaân
taùn quan saùt ñöôïc giöõa soá löôïng baûn quyeàn phaùt haønh vaø chi phí nghieân cöùu phaùt trieån (Hình
3.11) cho thaáy moái quan heä theo ñöôøng cong. Ta thaáy raèng giaû thieát tuyeán tính ñaõ cho döï ñoaùn
xaáu trong vaøi naêm. Beân caïnh caùc söï vieäc quan saùt thöïc nghieäm cuûa daïng naøy, thöôøng coøn coù
nhöõng lyù leõ lyù thuyeát toát cho vieäc xem xeùt caùc daïng haøm toång quaùt cuûa moái quan heä giöõa caùc
bieán phuï thuoäc vaø ñoäc laäp. Ví duï, lyù thuyeát kinh teá cho chuùng ta bieát raèng ñöôøng cong chi phí
trung bình coù daïng chöõ U, vaø do vaäy giaû thieát tuyeán tính laø ñaùng ngôø neáu ta muoán öôùc löôïng
ñöôøng cong chi phí trung bình.
Trong chöông naøy, chuùng ta khaûo saùt moät caùch chi tieát ñaùng keå caùc caùch thaønh laäp vaø öôùc
löôïng caùc quan heä phi tuyeán. Ñeå coù theå veõ caùc ñoà thò, nhieàu caùch trình baøy chæ giaûi quyeát duy
nhaát moät bieán giaûi thích. Ñaây chæ ñôn thuaàn laø moät phöông caùch mang tính sö phaïm. Trong caùc
ví duï vaø öùng duïng chuùng ta seõ giaûm nheï raøng buoäc naøy.
Chöông naøy cuõng thaûo luaän vaøi phöông phaùp tieán haønh caùc kieåm ñònh ñaëc tröng moâ hình
chính thöùc. Ñaëc bieät, caùc phöông phaùp “toång quaùt ñeán ñôn giaûn” vaø “ñôn giaûn ñeán toång quaùt”
ñöôïc ñeà caäp trong Chöông 1 seõ ñöôïc thaûo luaän, vaø goïi laø thuû tuïc Ramsey’s RESET (1969).

6.1 OÂn Laïi Caùc Haøm Logarit vaø Haøm Muõ

Caùc haøm muõ vaø logarit laø hai trong soá caùc haøm ñöôïc duøng phoå bieán nhaát trong laäp moâ hình. Vì
lyù do naøy, seõ höõu ích khi oân laïi nhöõng tính chaát cô baûn cuûa caùc haøm naøy tröôùc khi söû duïng
chuùng.
Haøm Y = aX (a > 0) laø moät ví duï cuûa moät haøm muõ. Trong haøm naøy, a laø cô soá cuûa haøm vaø
X laø soá muõ. Trong toaùn hoïc, cô soá thoâng thöôøng nhaát duøng trong moät haøm muõ laø haèng soá toaùn
hoïc e ñöôïc xaùc ñònh bôûi

Ramu Ramanathan 1 Thuïc Ñoan/Haøo Thi


n
 1
e = lim1 +  = 2,71828...
n →∞
 n
X
Vaäy haøm muõ chuaån coù daïng Y = e , vaø cuõng ñöôïc vieát döôùi daïng exp(X). Haøm nghòch cuûa
haøm muõ goïi laø haøm logarit. Logarit cô soá a cho tröôùc (phaûi laø soá döông) cuûa moät soá ñöôïc ñònh
nghóa laø khi luõy thöøa logarit cuûa cô soá seõ cho chính soá ñoù. Ta vieát X = logaY. Ví duï, vì 32 = 25,
logarit cô soá 2 cuûa 32 laø 5. Logarit cô soá e ñöôïc goïi logarit töï nhieân vaø kyù hieäu laø Y = lnX,
maø khoâng caàn ghi roõ cô soá. Löu yù raèng ln 1 = 0 bôûi vì e0 = 1. Moät soá tính chaát cuûa haøm muõ vaø
logarit ñöôïc lieät keâ döôùi ñaây.

Tính chaát 6.1
a. Haøm logarit vaø haøm muõ laø ñôn ñieäu taêng; nghóa laø, neáu a > b, thì f(a) > f(b), vaø ngöôïc laïi.
b. Logarit cuûa tích hai soá baèng toång logarit; nghóa laø, ln(XY) = lnX + lnY. Cuõng vaäy, logarit
cuûa tyû soá laø hieäu cuûa caùc logarit. Vaäy, ln(X/Y) = lnX – lnY. Theo ñoù ln(1/X) = – lnX.
c. ln(aX) = Xln a. Theo ñoù aX = eXln a.
d. aXaY = aX+Y vaø (aX)Y = aXY.

Khoâng nhö ñöôøng thaúng, coù ñoä doác khoâng ñoåi, haøm soá toång quaùt f(X), nhö haøm muõ vaø logarit,
coù ñoä doác thay ñoåi. Söï thay ñoåi cuûa Y theo thay ñoåi ñôn vò cuûa X laø taùc ñoäng caän bieân cuûa X
leân Y vaø thöôøng kyù hieäu bôûi ∆Y/∆X (xem Hình 2.A vaø phaàn thaûo luaän lieân quan). Neáu söï thay
ñoåi cuûa X voâ cuøng nhoû, ta coù ñoä doác cuûa tieáp tuyeán cuûa ñöôøng cong f(X) taïi ñieåm X. Ñoä doác
giôùi haïn naøy ñöôïc xem laø ñaïo haøm cuûa Y ñoái vôùi X vaø ñöôïc kyù hieäu bôûi dY/dX. Vaäy ñaïo haøm
laø taùc ñoäng caän bieân cuûa X leân Y vôùi söï thay ñoåi raát nhoû cuûa X. Ñoù laø moät khaùi nieäm voâ cuøng
quan troïng trong kinh teá löôïng, bôûi vì ta luoân hoûi söï thay ñoåi kyø voïng cuûa bieán phuï thuoäc laø gì
khi ta thay ñoåi giaù trò cuûa moät bieán ñoäc laäp vôùi moät löôïng raát nhoû. Caùc tính chaát cuûa caùc ñaïo
haøm ñöôïc toùm taét trong Tính chaát 2.A.5 vaø ñaùng ñeå nghieân cöùu. Tính chaát 6.2 lieät keâ moät ít
tính chaát cuûa haøm muõ vaø logarit maø raát höõu ích trong kinh teá löôïng. Hình 6.1 minh hoïa baèng ñoà
thò hai haøm soá naøy.

Tính chaát 6.2
a. Haøm muõ vôùi cô soá e coù tính chaát ñaëc bieät laø noù baèng vôùi ñaïo haøm cuûa chính noù. Vaäy, neáu Y
= eX, thì dY/dX = eX.
b. Ñaïo haøm cuûa eaX laø aeaX.
c. Ñaïo haøm cuûa ln X baèng 1/X.
d. Ñaïo haøm cuûa aX baèng aXln a. Keát quaû naøy coù ñöôïc töø cô sôû laø aX = eXlna vaø tính chaát ñaïo
haøm cuûa ebX = bebX.



Hình 6.1 Ñoà Thò cuûa Haøm Muõ vaø Logarit

exp (X)
25

20

15

10

5

0
X
0 0.5 1 1.5 2 2.5 3

a. Ñoà thò cuûa Y = exp(X)

ln (X)
1.5

1

0.5

0 X
0 0.5 1 1.5 2 2.5 3
-0.5

-1

-1.5

-2

-2.5

b. Ñoà thò cuûa Y = ln(X)



Khaùi Nieäm cuûa Ñoä Co Giaõn

Logarit coù töông quan raát gaàn vôùi khaùi nieäm cuûa ñoä co giaõn ñöôïc duøng trong kinh teá. Ta seõ
thaáy trong caùc phaàn sau raèng khaùi nieäm naøy cuõng ñöôïc söû duïng roäng raõi trong kinh teá löôïng
thöïc nghieäm. Theo thuaät ngöõ ñôn giaûn, ñoä co giaõn cuûa Y ñoái vôùi X ñöôïc ñònh nghóa laø phaàn
traêm thay ñoåi cuûa Y ñoái vôùi moät phaàn traêm thay ñoåi cuûa X cho moät thay ñoåi nhoû cuûa X. Vaäy neáu
∆Y laø söï thay ñoåi cuûa Y, phaàn traêm thay ñoåi laø 100∆Y/Y. Töông töï, 100∆X/X laø phaàn traêm
thay ñoåi cuûa X. Tyû soá cuûa soá ñaàu ñoái vôùi soá sau laø ñoä co giaõn. Ñieàu naøy ñöa ñeán ñònh nghóa
sau.

Baûng 6.1 Caùc Taùc Ñoäng Caän Bieân vaø Ñoä Co Giaõn cuûa caùc Daïng Haøm Khaùc Nhau

Teân Daïng Haøm Taùc Ñoäng Caän Bieân Ñoä Co Giaõn
(dY/dX) [(X/Y)(dY/dX)]
Tuyeán tính Y = β1 + β2X β2 β2X/Y
Logarit – tuyeán tính Y = β1 + β2 lnX β2/X β2/Y
Nghòch ñaûo Y = β1 + β2 (1/X) – β2/X2 – β2/(XY)
Baäc hai Y = β1 + β2X + β3X2 β2 + 2β3X (β2 + 2β3X)X/Y
Töông taùc Y = β1 + β2X + β3XZ β2 + β3Z (β2 + β3Z)X/Y
Tuyeán tính-logarit lnY = β1 + β2X β2Y β2X
Nghòch ñaûo – logarit lnY = β1 + β2 (1/X) – β2 Y/X2 – β2/X
Baäc hai – logarit lnY = β1 + β2X + β3X2 Y(β2 + 2β3X) X(β2 + 2β3X)
Log-hai laàn lnY = β1 + β2 lnX β2Y/X β2
(log-log)
Logistic  Y  β2Y(1-Y) β2(1-Y)X
ln   = β1 + β 2 X
1 − Y 

ÑÒNH NGHÓA 6.1

Ñoä co giaõn cuûa Y ñoái vôùi X (kyù hieäu laø η) laø

∆Y ∆X X ∆Y X dY
η= ÷ = → khi ∆X tieán veà 0. (6.1)
Y X Y ∆X Y dX

Baûng 6.1 coù caùc taùc ñoäng öùng caän bieân (dY/dX) vaø ñoä co giaõn [(X/Y)(dY/dX)] cuûa moät soá
daïng haøm coù theå choïn löïa trong chöông naøy. Löu yù raèng ñoâi khi caùc keát quaû naøy phuï thuoäc vaøo
X vaø/hoaëc Y. Ñeå tính toaùn chuùng, ngöôøi ta thöôøng thay theá giaù trò trung bình X vaø giaù trò döï
ˆ
ñoaùn töông öùng Y .

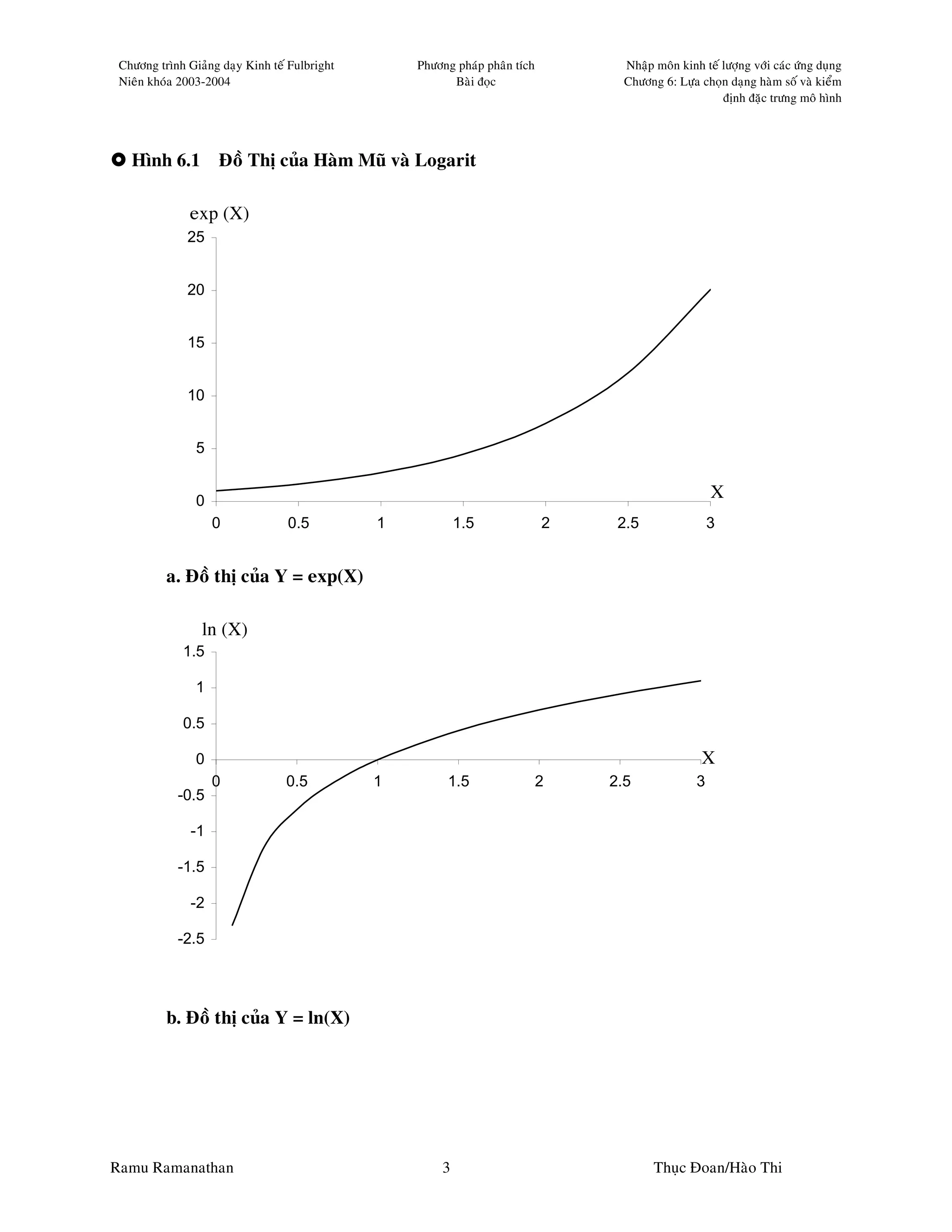
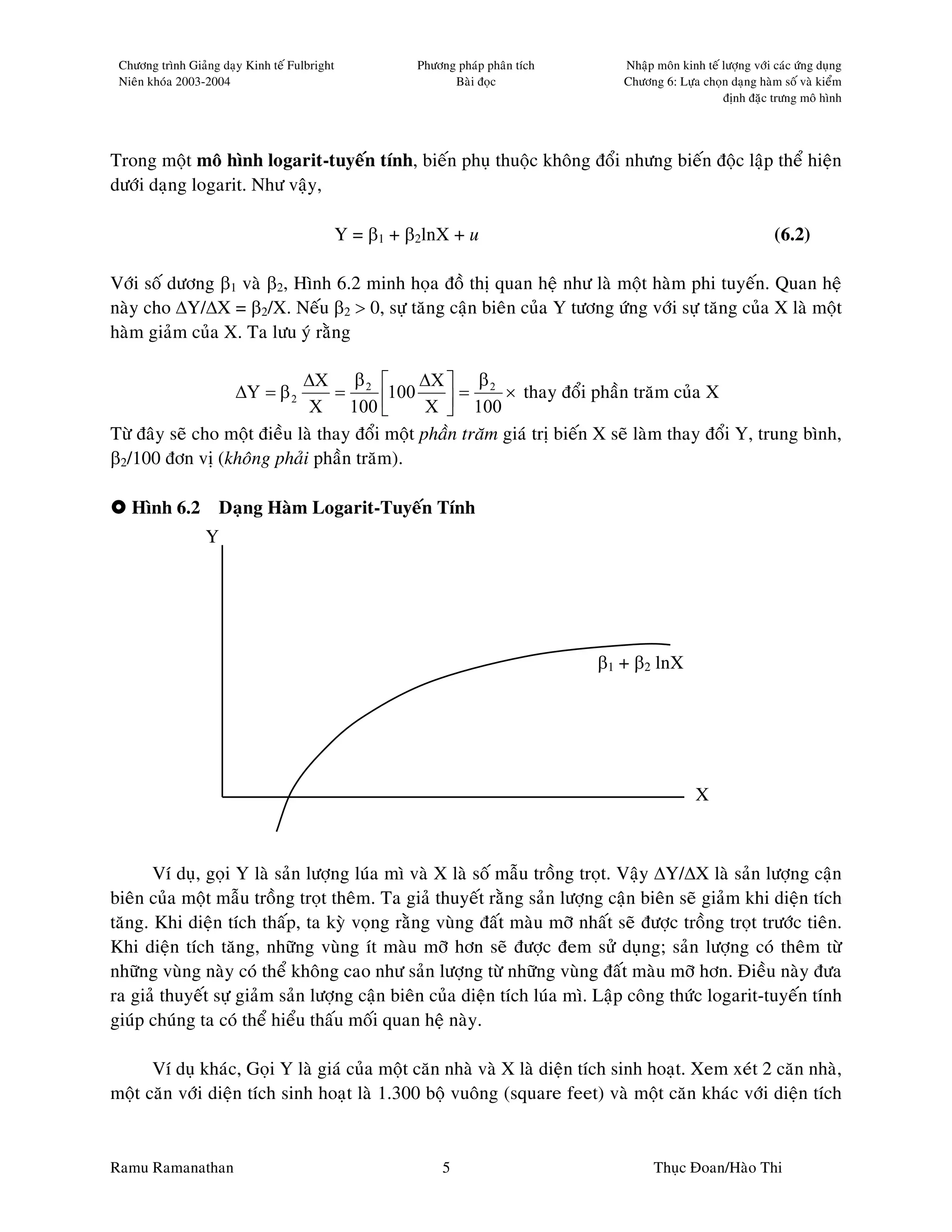
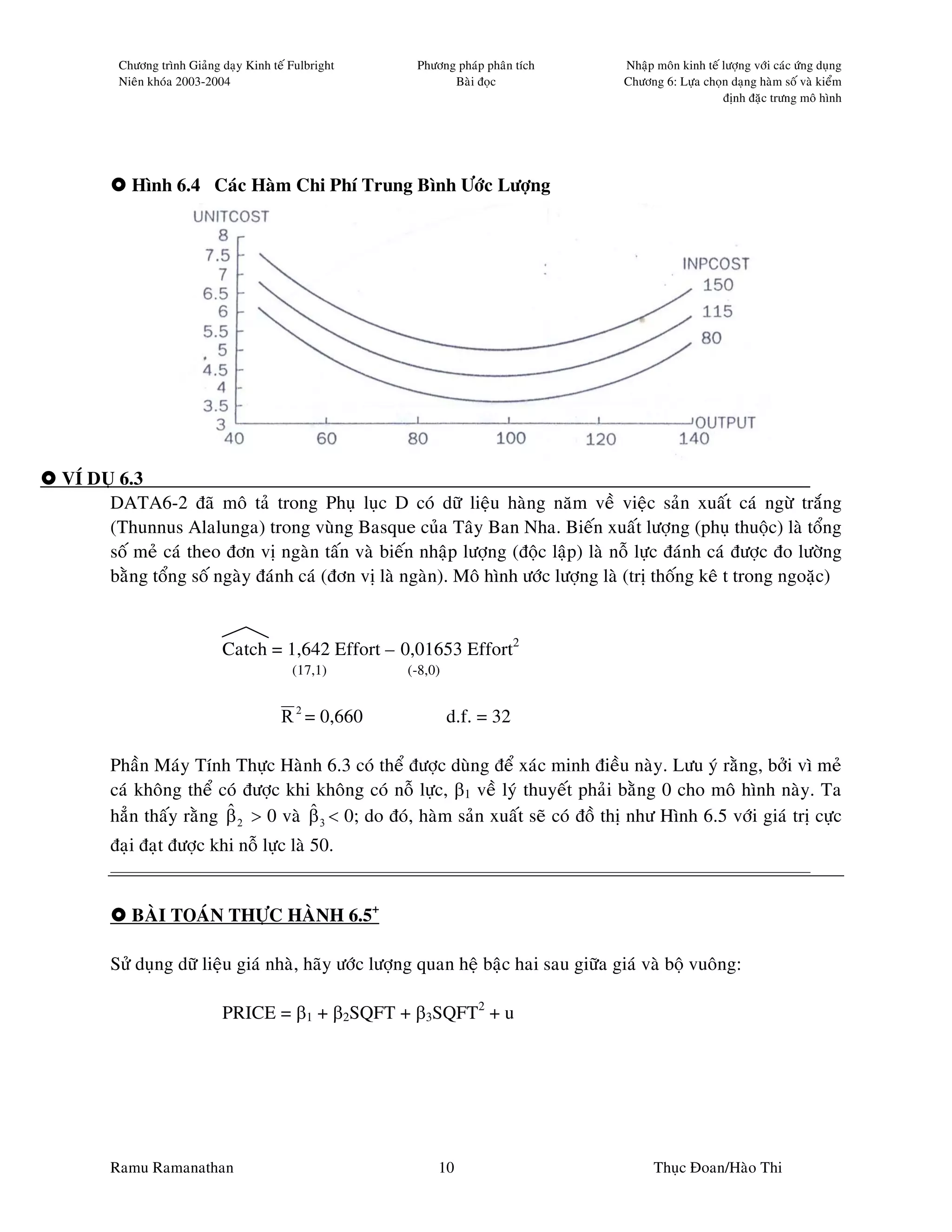
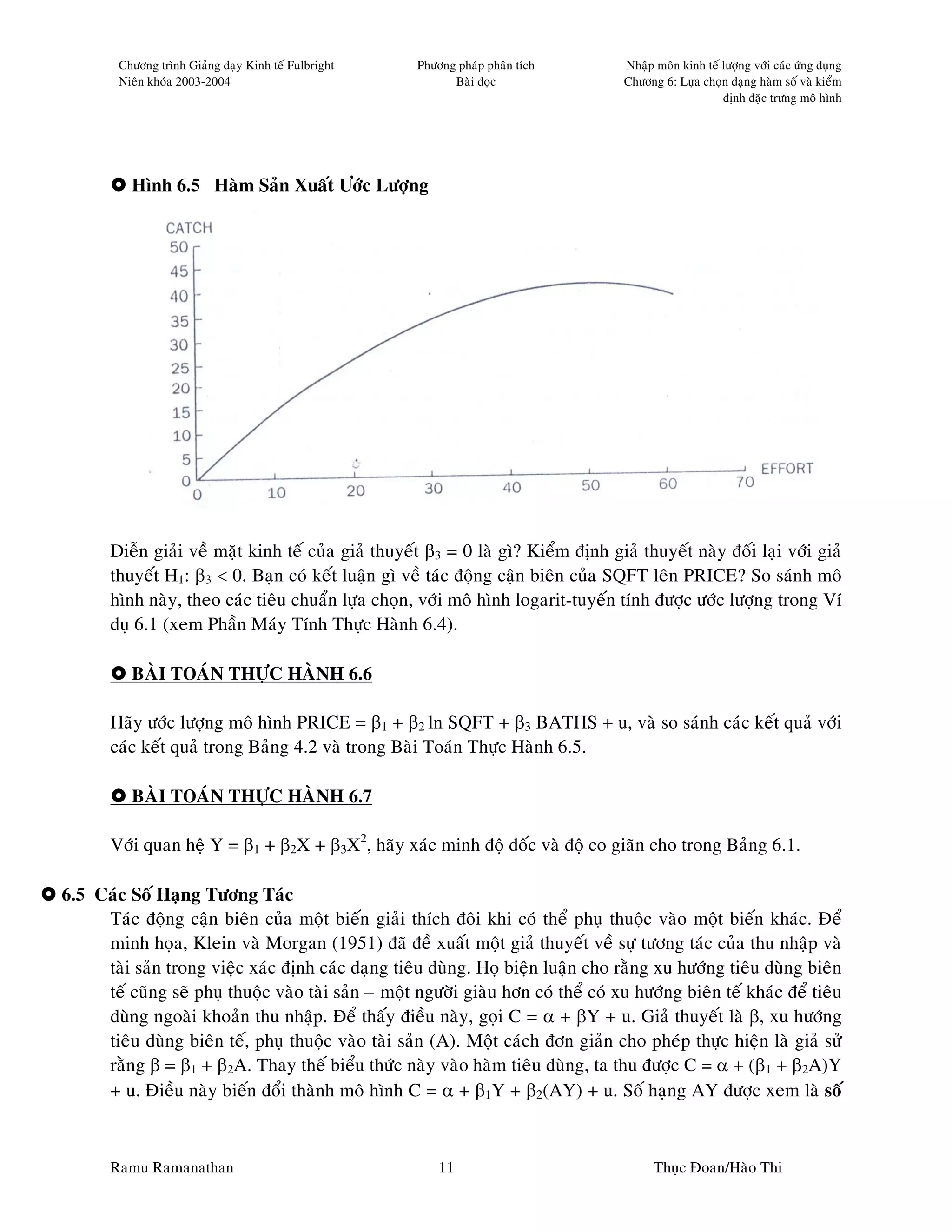
6.2 Quan Heä Logarit-Tuyeán Tính



Trong moät moâ hình logarit-tuyeán tính, bieán phuï thuoäc khoâng ñoåi nhöng bieán ñoäc laäp theå hieän
döôùi daïng logarit. Nhö vaäy,

Y = β1 + β2lnX + u (6.2)

Vôùi soá döông β1 vaø β2, Hình 6.2 minh hoïa ñoà thò quan heä nhö laø moät haøm phi tuyeán. Quan heä
naøy cho ∆Y/∆X = β2/X. Neáu β2 > 0, söï taêng caän bieân cuûa Y töông öùng vôùi söï taêng cuûa X laø moät
haøm giaûm cuûa X. Ta löu yù raèng

∆X β 2  ∆X  β 2
∆Y = β 2 = 100 = × thay ñoåi phaàn traêm cuûa X
X 100   X  100

Töø ñaây seõ cho moät ñieàu laø thay ñoåi moät phaàn traêm giaù trò bieán X seõ laøm thay ñoåi Y, trung bình,
β2/100 ñôn vò (khoâng phaûi phaàn traêm).

Hình 6.2 Daïng Haøm Logarit-Tuyeán Tính
Y

β1 + β2 lnX

X

Ví duï, goïi Y laø saûn löôïng luùa mì vaø X laø soá maãu troàng troït. Vaäy ∆Y/∆X laø saûn löôïng caän
bieân cuûa moät maãu troàng troït theâm. Ta giaû thuyeát raèng saûn löôïng caän bieân seõ giaûm khi dieän tích
taêng. Khi dieän tích thaáp, ta kyø voïng raèng vuøng ñaát maøu môõ nhaát seõ ñöôïc troàng troït tröôùc tieân.
Khi dieän tích taêng, nhöõng vuøng ít maøu môõ hôn seõ ñöôïc ñem söû duïng; saûn löôïng coù theâm töø
nhöõng vuøng naøy coù theå khoâng cao nhö saûn löôïng töø nhöõng vuøng ñaát maøu môõ hôn. Ñieàu naøy ñöa
ra giaû thuyeát söï giaûm saûn löôïng caän bieân cuûa dieän tích luùa mì. Laäp coâng thöùc logarit-tuyeán tính
giuùp chuùng ta coù theå hieåu thaáu moái quan heä naøy.

Ví duï khaùc, Goïi Y laø giaù cuûa moät caên nhaø vaø X laø dieän tích sinh hoaït. Xem xeùt 2 caên nhaø,
moät caên vôùi dieän tích sinh hoaït laø 1.300 boä vuoâng (square feet) vaø moät caên khaùc vôùi dieän tích



sinh hoaït 3.200 boä vuoâng. Ta kyø voïng raèng phaàn giaù taêng theâm maø moät ngöôøi tieâu duøng seõ saün
saøng traû cho 100 boä vuoâng theâm vaøo dieän tích sinh hoaït seõ cao khi X = 1.300 hôn laø khi X =
3.200. Ñieàu naøy laø bôûi vì caên nhaø sau ñaõ roäng saün, vaø ngöôøi mua coù theå khoâng muoán traû theâm
nhieàu ñeå taêng theâm dieän tích. Ñieàu naøy coù nghóa raèng taùc ñoäng caän bieân cuûa SQFT (dieän tích)
leân PRICE (giaù) kyø voïng seõ giaûm khi SQFT taêng. Moät caùch ñeå kieåm ñònh ñieàu naøy laø ñieàu
chænh moät moâ hình logarit-tuyeán tính vaø kieåm ñònh giaû thuyeát H0: β2 = 0 ñoái laïi giaû thuyeát H1:
β2 > 0. Ñieàu naøy seõ ñöôïc nhìn nhaän nhö laø moät kieåm ñònh moät phía. Quy taéc ra quyeát ñònh laø
baùc boû H0 neáu tc > t* n-2 (0,05). Ta löu yù töø Baûng 6.1 raèng trong moâ hình naøy ñoä co giaõn cuûa Y
ñoái vôùi X laø β2/Y. Ta coù theå tính toaùn ñoä co giaõn taïi giaù trò trung bình laø β2/ Y . Neáu döõ lieäu laø
chuoãi thôøi gian, ñoä co giaõn ñaùng quan taâm hôn laø ñoä co giaõn töông öùng vôùi quan saùt gaàn ñaây
nhaát – vôùi t = n. Ñoä co giaõn naøy laø β2/Yn.

Maëc duø nhöõng ví duï minh hoïa naøy vaãn laø caùc daïng moâ hình hoài qui ñôn giaûn, phaàn môû
roäng theâm cho tröôøng hôïp ña bieán laø khoâng phöùc taïp. Ñôn giaûn laø phaùt ra caùc logarit cuûa caùc
bieán giaûi thích thích hôïp, goïi chuùng laø Z1, Z2 v.v… vaø hoài qui bieán Y theo moät haèng soá vaø caùc
bieán Z.

BAØI TOAÙN THÖÏC HAØNH 6.1
Tìm bieåu thöùc ñoä co giaõn cuûa Y ñoái vôùi X trong caùc moâ hình tuyeán tính vaø phi tuyeán vaø chöùng
minh caùc muïc trong Baûng 6.1.

Veõ ñoà thò Phöông trình (6.2) khi β2 < 0 (ñeå ñôn giaûn giaû söû raèng β1 = 0).

VÍ DUÏ 6.1
Ta ñaõ öôùc löôïng moâ hình logarit-tuyeán tính söû duïng döõ lieäu giaù nhaø trong Baûng 4.1 (xem Phaàn
Maùy Tính Thöïc Haønh 6.1 giôùi thieäu caùch chaïy laïi caùc keát quaû cuûa ví duï naøy vaø kieåm tra nhöõng
khaúng ñònh ñaõ thöïc hieän ôû ñaây). Söï bieän luaän veà söï giaûm taùc ñoäng caän bieân aùp duïng nhö nhau
cho soá phoøng nguû vaø soá phoøng taém. Vì vaäy ta ñaõ phaùt ra caùc logarit cuûa caùc bieán SQFT,
BEDRMS, vaø BATHS vaø keá tieáp ñaõ hoài qui bieán PRICE theo moät haèng soá vaø nhöõng soá haïng
logarit naøy. Keá ñeán logarit cuûa BATHS vaø BEDRMS ñöôïc loaïi boû moãi laàn töøng bieán moät bôûi
vì heä soá cuûa chuùng raát khoâng coù yù nghóa. Moâ hình “toát nhaát” ñaõ ñöôïc choïn theo caùc tieâu chuaån
löïa choïn ñaõ thaûo luaän trong Chöông 4. Caùc phöông trình öôùc löôïng cuûa moâ hình tuyeán tính toát
nhaát vaø moâ hình logarit-tuyeán tính toát nhaát seõ ñöôïc trình baøy tieáp sau, vôùi caùc trò thoáng keâ t
trong ngoaëc.



PRICE = 52,351 + 0,139 SQFT
(1,4) (7,4)

R 2 = 0,806 d.f. = 12

PRICE = –1.749,974 + 299,972 ln(SQFT) – 145,094 ln(BEDRMS)
(-6,8) (7,5) (-1,7)

R 2 = 0,826 d.f. = 11

Ta löu yù raèng giaù trò R 2 hôi cao hôn ñoái vôùi moâ hình logarit-tuyeán tính. Moâ hình naøy cuõng
coù caùc trò thoáng keâ löïa choïn moâ hình thaáp nhaát. Tuy nhieân, heä soá cho logarit cuûa BEDRMS chæ
coù yù nghóa ôû möùc 11,48 phaàn traêm. Neáu soá haïng naøy bò loaïi boû, caùc trò thoáng keâ löïa choïn seõ
xaáu ñi ñaùng keå, vaø do ñoù ta ñaõ choïn giöõ noù laïi. Heä soá hoài qui cho ln(SQFT) coù yù nghóa cao, vaäy
uûng hoä cho giaû thuyeát raèng taùc ñoäng caän bieân cuûa dieän tích sinh hoaït giaûm khi soá boä vuoâng
taêng. Heä soá cho logarit cuûa BEDRMS coù giaù trò aâm gioáng nhö ñoái vôùi moâ hình tuyeán tính,
nhöng taùc ñoäng cuûa heä soá naøy laø yeáu veà maët thoáng keâ.

Tính ñoä co giaõn töøng phaàn cuûa PRICE ñoái vôùi SQFT cho caùc moâ hình öôùc löôïng logarit-tuyeán
tính vaø tuyeán tính khi SQFT laø 1.500, 2.000 vaø 2.500. Laøm theá naøo chuùng so saùnh vôùi nhau?

Hình 6.3 Quan Heä Nghòch Ñaûo

Y

β1
X



6.3 Bieán Ñoåi Nghòch Ñaûo

Moät daïng haøm thöôøng ñöôïc söû duïng ñeå öôùc löôïng ñöôøng cong nhu caàu laø haøm bieán ñoåi nghòch
ñaûo:

1
Y = β1 + β 2   + u
X
Bôûi vì ñöôøng cong nhu caàu ñaëc thuø doác xuoáng, ta kyø voïng β2 laø döông. Löu yù raèng khi X trôû
neân lôùn, Y tieäm caän tieán gaàn vôùi β1 (xem Hình 6.3). Daáu vaø ñoä lôùn cuûa β1 seõ xaùc ñònh ñöôøng
cong coù caét truïc X hay khoâng.

Veõ ñoà thò haøm nghòch ñaûo vôùi β2 < 0, β1 > 0.

6.4 Thích Hôïp Ñöôøng Cong Ña Thöùc

Caùc nhaø nghieân cöùu raát thöôøng duøng moät ña thöùc ñeå lieân heä moät bieán phuï thuoäc vôùi moät bieán
ñoäc laäp. Moâ hình naøy coù theå laø

Y = β1 + β2X + β3X2 + β4X3 + . . . + βk+1Xk + u

Thuû tuïc öôùc löôïng bao goàm taïo caùc bieán môùi X2, X3, v.v… qua caùc pheùp bieán ñoåi vaø keá ñeán hoài
qui Y theo moät soá haïng haèng soá, theo X, vaø theo caùc bieán ñaõ bieán ñoåi naøy. Möùc ña thöùc (k) bò
raøng buoäc bôûi soá quan saùt. Neáu k = 3, ta coù quan heä baäc ba; vaø neáu k = 2, ta coù coâng thöùc baäc
hai. Caùc coâng thöùc baäc hai thöôøng ñöôïc söû duïng ñeå ñieàu chænh caùc haøm chi phí coù daïng chöõ U
vaø caùc quan heä phi tuyeán khaùc. Moät ñöôøng cong baäc ba thöôøng ñöôïc laøm thích hôïp gaàn ñuùng
vôùi hình daïng trong Hình 6.9 (xem phaàn moâ hình logit). Nhìn chung, baäc ña thöùc lôùn hôn 2 neân
traùnh. Moät trong caùc lyù do laø thöïc teá moãi soá haïng ña thöùc ñoàng nghóa vôùi vieäc maát ñi theâm moät
baäc töï do. Nhö ñaõ ñeà caäp trong Chöông 3, söï maát ñi baäc töï do nghóa laø giaûm söï chính xaùc cuûa
caùc öôùc löôïng caùc thoâng soá vaø giaûm khaû naêng cuûa caùc kieåm ñònh. Cuõng vaäy, ta ñaõ thaáy trong
Chöông 5 raèng moái töông quan cao coù theå coù giöõa X, X2, vaø X3 laøm cho caùc heä soá rieâng leû keùm
tin caäy hôn.
Söû duïng caùc tính chaát veà ñaïo haøm (xem Tính chaát 2.A.5), ta coù theå cho thaáy raèng taùc
ñoäng caän bieân cuûa X leân Y ñöôïc xaùc ñònh bôûi

dY/dX = β2 + 2β3X + 3β4X2 + . . . + kβk+1Xk-1



Moät tröôøng hôïp ñaëc bieät cuûa daïng haøm ña thöùc laø moâ hình baäc hai

Y = β 1 + β 2X + β 3X 2 + u

Taùc ñoäng caän bieân cuûa X leân Y, nghóa laø ñoä doác cuûa quan heä baäc hai, ñöôïc xaùc ñònh bôûi
dY/dX = β2 + 2β3X. Löu yù raèng taùc ñoäng caän bieân cuûa X leân Y phuï thuoäc vaøo giaù trò cuûa X maø
taïi ñoù ta tính taùc ñoäng caän bieân. Moät giaù trò phoå bieán ñöôïc duøng laø giaù trò trung bình, X . Nhö
ñaõ cho thaáy trong phuï luïc Chöông 2, khi dY/dX = 0, haøm soá seõ hoaëc ñaït cöïc ñaïi hoaëc cöïc tieåu.
Giaù trò X taïi ñoù xaûy ra ñieàu naøy seõ coù ñöôïc töø vieäc giaûi ñieàu kieän β2 + 2β3X = 0 khi X0 = –
β2/(2β3). Ñeå xaùc ñònh xem haøm ñaït cöïc tieåu hay cöïc ñaïi, ta caàn phaûi tính ñaïo haøm baäc hai,
d2Y/dX2 = 2β3. Neáu β3 < 0, haøm soá seõ ñaït cöïc ñaïi taïi X0, vaø neáu β3 döông, haøm ñaït cöïc tieåu taïi
X0. Tieáp theo ta trình baøy hai ví duï: moät haøm chi phí trung bình coù quan heä daïng chöõ U (Hình
6.4) vaø moät haøm saûn xuaát coù quan heä daïng ñöôøng cong loài (hump-shaped) (Hình 6.5).

VÍ DUÏ 6.2
DATA6-1 ñaõ moâ taû trong Phuï luïc D coù döõ lieäu veà chi phí ñôn vò (UNITCOST) cuûa moät coâng ty
saûn xuaát treân moät thôøi ñoaïn 20 naêm, moät chæ soá xuaát löôïng cuûa coâng ty (OUTPUT), vaø moät chæ
soá chi phí nhaäp löôïng cuûa coâng ty (INPCOST). Tröôùc heát ta coù bình phöông hai bieán ñoäc laäp
vaø keá ñeán hoài qui UNICOST theo moät haèng soá, OUTPUT, OUTPUT2, INPCOST, vaø
INPCOST 2 (xem Phaàn Maùy Tính Thöïc Haønh 6.2 ñeå bieát theâm chi tieát veà ñieàu naøy). Bôûi vì
INPCOST2 coù heä soá voâ cuøng khoâng coù yù nghóa, noù bò loaïi boû vaø moâ hình ñöôïc öôùc löôïng laïi.

Caùc keát quaû ñöôïc cho sau ñaây, vôùi caùc trò thoáng keâ t trong ngoaëc.

UNITCOST = 10,522 – 0,175 OUTPUT + 0,000895 OUTPUT2
(14,3) (- 9,7) (7,8)
+ 0,0202 INPCOST
(14,454)

R 2 = 0,978 d.f. = 16

ˆ ˆ ˆ
Löu yù raèng ñoái vôùi moâ hình naøy β1 , β 3 > 0 vaø β 2 < 0, giaûi thích cho quan heä daïng chöõ U. Moâ
hình giaûi thích 97,8 phaàn traêm söï thay ñoåi trong chi phí trung bình. Deã daøng chöùng minh raèng
taát caû caùc heä soá hoài qui ñeàu voâ cuøng coù yù nghóa. Löu yù raèng nhöõng gì ta coù treân ñaây laø moät hoï
caùc ñöôøng cong chi phí trung bình ñöôïc di chuyeån theo caùc möùc chæ soá chi phí nhaäp löôïng.
Cuõng raát höõu ích khi veõ ñoà thò haøm chi phí ñôn vò cho moät chi phí nhaäp löôïng tieâu bieåu. Hình
6.4 laø haøm chi phí trung bình coù daïng chöõ U öôùc löôïng cho moät daõy xuaát löôïng vaø 3 möùc chi
phí nhaäp löôïng khaùc nhau (80, 115, vaø 150). Chuùng ñaït giaù trò nhoû nhaát taïi chæ soá xuaát löôïng
coù möùc 98 (haõy xaùc minh).



Hình 6.4 Caùc Haøm Chi Phí Trung Bình Öôùc Löôïng

VÍ DUÏ 6.3
DATA6-2 ñaõ moâ taû trong Phuï luïc D coù döõ lieäu haøng naêm veà vieäc saûn xuaát caù ngöø traéng
(Thunnus Alalunga) trong vuøng Basque cuûa Taây Ban Nha. Bieán xuaát löôïng (phuï thuoäc) laø toång
soá meû caù theo ñôn vò ngaøn taán vaø bieán nhaäp löôïng (ñoäc laäp) laø noã löïc ñaùnh caù ñöôïc ño löôøng
baèng toång soá ngaøy ñaùnh caù (ñôn vò laø ngaøn). Moâ hình öôùc löôïng laø (trò thoáng keâ t trong ngoaëc)

Catch = 1,642 Effort – 0,01653 Effort2
(17,1) (-8,0)

R 2 = 0,660 d.f. = 32

Phaàn Maùy Tính Thöïc Haønh 6.3 coù theå ñöôïc duøng ñeå xaùc minh ñieàu naøy. Löu yù raèng, bôûi vì meû
caù khoâng theå coù ñöôïc khi khoâng coù noã löïc, β1 veà lyù thuyeát phaûi baèng 0 cho moâ hình naøy. Ta
ˆ ˆ
haún thaáy raèng β 2 > 0 vaø β 3 < 0; do ñoù, haøm saûn xuaát seõ coù ñoà thò nhö Hình 6.5 vôùi giaù trò cöïc
ñaïi ñaït ñöôïc khi noã löïc laø 50.

BAØI TOAÙN THÖÏC HAØNH 6.5+

Söû duïng döõ lieäu giaù nhaø, haõy öôùc löôïng quan heä baäc hai sau giöõa giaù vaø boä vuoâng:

PRICE = β1 + β2SQFT + β3SQFT2 + u



Hình 6.5 Haøm Saûn Xuaát Öôùc Löôïng

Dieãn giaûi veà maët kinh teá cuûa giaû thuyeát β3 = 0 laø gì? Kieåm ñònh giaû thuyeát naøy ñoái laïi vôùi giaû
thuyeát H1: β3 < 0. Baïn coù keát luaän gì veà taùc ñoäng caän bieân cuûa SQFT leân PRICE? So saùnh moâ
hình naøy, theo caùc tieâu chuaån löïa choïn, vôùi moâ hình logarit-tuyeán tính ñöôïc öôùc löôïng trong Ví
duï 6.1 (xem Phaàn Maùy Tính Thöïc Haønh 6.4).


Haõy öôùc löôïng moâ hình PRICE = β1 + β2 ln SQFT + β3 BATHS + u, vaø so saùnh caùc keát quaû vôùi
caùc keát quaû trong Baûng 4.2 vaø trong Baøi Toaùn Thöïc Haønh 6.5.


Vôùi quan heä Y = β1 + β2X + β3X2, haõy xaùc minh ñoä doác vaø ñoä co giaõn cho trong Baûng 6.1.

6.5 Caùc Soá Haïng Töông Taùc
Taùc ñoäng caän bieân cuûa moät bieán giaûi thích ñoâi khi coù theå phuï thuoäc vaøo moät bieán khaùc. Ñeå
minh hoïa, Klein vaø Morgan (1951) ñaõ ñeà xuaát moät giaû thuyeát veà söï töông taùc cuûa thu nhaäp vaø
taøi saûn trong vieäc xaùc ñònh caùc daïng tieâu duøng. Hoï bieän luaän cho raèng xu höôùng tieâu duøng bieân
teá cuõng seõ phuï thuoäc vaøo taøi saûn – moät ngöôøi giaøu hôn coù theå coù xu höôùng bieân teá khaùc ñeå tieâu
duøng ngoaøi khoaûn thu nhaäp. Ñeå thaáy ñieàu naøy, goïi C = α + βY + u. Giaû thuyeát laø β, xu höôùng
tieâu duøng bieân teá, phuï thuoäc vaøo taøi saûn (A). Moät caùch ñôn giaûn cho pheùp thöïc hieän laø giaû söû
raèng β = β1 + β2A. Thay theá bieåu thöùc naøy vaøo haøm tieâu duøng, ta thu ñöôïc C = α + (β1 + β2A)Y
+ u. Ñieàu naøy bieán ñoåi thaønh moâ hình C = α + β1Y + β2(AY) + u. Soá haïng AY ñöôïc xem laø soá



haïng töông taùc bôûi vì noù bao goäp söï töông taùc giöõa caùc taùc ñoäng cuûa thu nhaäp vaø taøi saûn.
Nhaèm muïc ñích öôùc löôïng, ta taïo ra moät bieán môùi Z, baèng vôùi tích cuûa Y vaø A, vaø keá ñeán hoài
qui C theo moät haèng soá, Y, vaø Z. Neáu β2 coù yù nghóa veà maët thoáng keâ, thì coù daáu hieäu veà söï
töông taùc giöõa thu nhaäp vaø taøi saûn. Löu yù raèng trong ví duï naøy, ∆C/∆Y = β1 + β2A. Ñeå xaùc ñònh
taùc ñoäng caän bieân cuûa Y leân C, ta caàn coù giaù trò cuûa A.
Ví duï thöù hai, xeùt quan heä Et = α + βTt + ut, trong ñoù Et laø soá kilowatt giôø tieâu thuï ñieän vaø
Tt laø nhieät ñoä taïi thôøi ñieåm t. Neáu moâ hình naøy ñöôïc öôùc löôïng cho muøa heø, ta kyø voïng β seõ
döông bôûi vì, khi nhieät ñoä taêng vaøo muøa heø, thì nhu caàu duøng maùy laïnh seõ cao hôn vaø do ñoù
tieâu thuï ñieän seõ taêng. Tuy nhieân, ta coù theå giaû thuyeát raèng taùc ñoäng caän bieân cuûa T leân E coù theå
phuï thuoäc vaøo giaù ñieän (Pt). Neáu giaù ñieän laø ñaét, ngöôøi tieâu duøng coù theå hoaõn baät maùy laïnh
hoaëc taét sôùm hôn. Moät caùch ñeå kieåm ñònh taùc ñoäng naøy laø giaû söû raèng β = β1 + β2Pt. Vaäy ta
ñang giaû söû raèng taùc ñoäng caän bieân cuûa nhieät ñoä leân tieâu thuï ñieän phuï thuoäc vaøo giaù. Thay bieåu
thöùc naøy vaøo quan heä, ta coù

Et = α + (β1 + β2Pt)Tt + ut = α + β1Tt + β2(PtTt) + ut

Ñeå öôùc löôïng caùc thoâng soá, ta cho Zt = PtTt vaø hoài qui E theo moät haèng soá, T, vaø Z. Söï yù nghóa
cuûa β2 laø daáu hieäu cuûa moät taùc ñoäng töông hoã giöõa nhieät ñoä vaø giaù. Löu yù raèng ∆E/∆P = β2T;
nghóa laø, taùc ñoäng caän bieân cuûa P leân E phuï thuoäc vaøo nhieät ñoä. Neáu ta cho α cuõng phuï thuoäc
vaøo P, moâ hình trôû thaønh

Et = α1 + α2Pt + β1Tt + β2(PtTt) + ut

Trong caùc chöông sau, ta coù vaøi ví duï veà caùc taùc ñoäng töông hoã nhö vaäy.

Phi Tuyeán Giaû Taïo

Ñeå nhaän bieát söï phi tuyeán coù theå coù, ta coù theå thöû veõ ñoà thò Y theo moät bieán ñoäc laäp cuï theå (X)
vaø quan saùt xem coù söï phi tuyeán naøo xaûy ra hay khoâng. Ñaây laø thuû tuïc nguy hieåm bôûi vì noù coù
theå daãn ñeán ñaëc tröng sai moâ hình nghieâm troïng. Ví duï, giaû söû raèng Y laø tuyeán tính vôùi X, Z,
vaø soá haïng töông taùc XZ, vaäy ta coù

Y = β1 + β2X + β3Z + β4(XZ) + u vaø ∆Y/∆X = β2 + β4Z

Trong tính toaùn taùc ñoäng caän bieân cuûa X leân Y, ta xem Z laø coá ñònh. Löu yù raèng taùc ñoäng caän
bieân cuûa X leân Y, nghóa laø ñoä doác, phuï thuoäc vaøo Z. Bieåu ñoà phaân taùn quan saùt thöïc nghieäm,
giöõa Y vaø X coù theå nhìn gioáng nhö Hình 6.6, coù veû nhö laø quan heä logarit-tuyeán tính giöõa Y vaø
X. Trong thöïc teá, ñieàu naøy laø do hai quan heä tuyeán tính giöõa Y vaø X vôùi caùc giaù trò khaùc nhau
cuûa Z (Z1 vaø Z2). Vaäy, thay vì veõ ñoà thò thöïc nghieäm quan saùt bieán Y theo moãi bieán X, baïn neân



coá gaéng moâ hình hoaù quaù trình phaùt döõ lieäu (DGP) duøng lyù thuyeát vaø tröïc giaùc veà haønh vi cô
baûn vaø keá ñeán tieán haønh kieåm ñònh ñaëc tröng. Trong Phaàn 6.13, 6.14, vaø 6.15, ta thaûo luaän vaøi
phöông phaùp ñeå kieåm ñònh caùc ñaëc tröng hoài qui.

Hình 6.6 Moät Ví Duï cuûa Phi Tuyeán Giaû Taïo

6.6 Hieän Töôïng Treã Trong Haønh Vi (Caùc Moâ Hình Ñoäng)

Caùc taùc ñoäng kinh teá vaø caùc bieán khaùc hieám khi xaûy ra töùc thôøi; phaûi toán thôøi gian ñeå ngöôøi
tieâu duøng, nhaø saûn xuaát, vaø caùc taùc nhaân kinh teá khaùc phaûn öùng. Lyù thuyeát kinh teá vó moâ cho ta
bieát raèng toång saûn löôïng quoác daân (GNP) caân baèng (Y) ñöôïc xaùc ñònh bôûi moät soá bieán ngoaïi
sinh, ñaëc bieät, bôûi chi tieâu chính phuû (G), thueá (T), cung tieàn (M), xuaát khaåu (X) v.v…. Bôûi vì
hieäu öùng caân baèng chæ giaûm ñöôïc sau moät khoaûng thôøi gian, caùc moâ hình kinh teá löôïng duøng döõ
lieäu daïng chuoãi thôøi gian thöôøng ñöôïc thaønh laäp vôùi hieän töôïng treã trong haønh vi. Moät ví duï
cuûa moâ hình nhö vaäy cho nhö sau:

Yt = β1 + β2Gt + β3Gt-1 + β4Mt + β5Mt-1 + β6Tt + β7Tt-1 + β8Xt + β8Xt-1 + ut

Thuû tuïc öôùc löôïng ôû ñaây hoaøn toaøn ñôn giaûn. Ñôn giaûn ta taïo caùc bieán coù hieäu öùng treã Gt-
1, Mt-1, Tt-1 vaø Xt-1 vaø hoài qui Yt theo caùc bieán naøy duøng quan saùt töø 2 ñeán n. Bôûi vì Gt-1 vaø caùc
bieán khaùc khoâng ñöôïc ñònh nghóa cho t = 1, ta maát quan saùt thöù nhaát trong öôùc löôïng. Tuy
nhieân, moät soá vaán ñeà phaùt sinh trong moâ hình naøy bôûi vì caùc bieán ñoäc laäp töông quan vôùi nhau
vaø cuõng do bôûi vì baäc töï do bò maát khi coù nhieàu hieäu öùng treã hôn theâm vaøo. Nhöõng vaán ñeà naøy
ñöôïc thaûo luaän chi tieát trong Chöông 10.
Hieän töôïng treã trong haønh vi coù theå coù daïng hieän töôïng treã trong bieán phuï thuoäc. Moâ hình
coù theå coù daïng



Yt = β1 + β2Yt-1 + β3Xt + β4Xt-1 + ut

Ví duï, goïi Yt laø chi tieâu taïi thôøi ñieåm t vaø Xt laø thu nhaäp. Bôûi vì ngöôøi tieâu duøng coù xu höôùng
duy trì möùc tieâu chuaån soáng thöôøng leä, ta coù theå kyø voïng söï tieâu duøng cuûa hoï lieân quan maät
thieát vôùi söï tieâu duøng tröôùc ñaây cuûa hoï. Vì vaäy, chuùng ta coù theå kyø voïng laø Yt cuõng phuï thuoäc
vaøo Yt-1. Cuï theå hôn, xem phöông trình sau:

Yt = β1 + β2Yt-1 + β3(Xt – Xt-1) + ut

Vì “caùc taäp quaùn thoùi quen” neân noùi chung ngöôøi tieâu duøng mieãn cöôõng thay ñoåi loái soáng cuûa
hoï, vaø do ñoù chuùng ta kyø voïng möùc tieâu thuï taïi thôøi ñieåm t (Yt) phuï thuoäc vaøo möùc tieâu thuï ôû
giai ñoaïn tröôùc ñoù (Yt-1). Tuy nhieân, neáu möùc thu nhaäp (Xt) thay ñoåi, ngöôøi tieâu duøng seõ ñieàu
chænh haønh vi tieâu duøng cuûa hoï töông öùng vôùi söï taêng hoaëc giaûm thu nhaäp. Do vaäy chuùng ta seõ
duøng moâ hình ñoäng ñöôïc xaây döïng ôû treân vaø kyø voïng raèng taát caû caùc heä soá seõ coù giaù trò döông.

VÍ DUÏ 6.4

Taäp döõ lieäu DATA6-3 (xem Phuï luïc D) laø döõ lieäu veà chi tieâu tieâu duøng caù nhaân ñaàu ngöôøi cuûa
Vöông Quoác Anh (C, ño baèng baûng Anh) vaø thu nhaäp tuøy duïng ñaàu ngöôøi (nghóa laø, thu nhaäp
caù nhaân tröø thueá, kyù hieäu laø DI, vaø cuõng ñöôïc tính theo ñôn vò baûng Anh). Ñeå ñieàu chænh taùc
ñoäng cuûa laïm phaùt, caû hai bieán naøy ñöôïc bieåu dieãn theo giaù trò thöïc (coøn ñöôïc goïi laø giaù khoâng
ñoåi). Moâ hình ñoäng öôùc löôïng ñöôïc trình baøy döôùi ñaây (xem Phaàn Thöïc Haønh Maùy Tính 6.5),
vôùi trò thoáng keâ t trong ngoaëc ñôn.

ˆ
C t = -46,802 + 1,022Ct-1 + 0,706 (DIt – DIt-1)
(-2.07) (123.0) (9.93)

R 2 = 0,998 df = 38

Maëc duø moâ hình ñaït ñöôïc söï thích hôïp raát toát vaø caùc öôùc löôïng coù veû hôïp lyù, moâ hình naøy coù
moät soá trôû ngaïi. Nhö seõ thaáy ôû Chöông 10 vaø 13 raèng moâ hình naøy vi phaïm tính ñoäc laäp chuoãi
cuûa Giaû thieát 3.6 vaø Giaû thieát 3.4 laø caùc bieán ñoäc laäp khoâng ñöôïc töông quan vôùi caùc soá haïng
sai soá. Ñaëc tröng sai naøy seõ laøm cho caùc trò öôùc löôïng bò thieân leäch. Chuùng ta seõ xem xeùt laïi
moâ hình naøy trong caùc chöông 10 vaø 13.

6.7 ÖÙng duïng: Quan Heä Giöõa Soá Baèng Saùng Cheá Vaø Chi Tieâu R&D (ñaõ duyeät laïi)



Trong Phaàn 3.11, chuùng ta ñaõ öôùc löôïng moâ hình hoài quy tuyeán tính ñôn giöõa soá baèng saùng cheá
vaø chi tieâu cho R&D vaø bieát raèng moâ hình naøy laø hoaøn toaøn khoâng ñuû vì bieåu ñoà phaân taùn cuûa
caùc giaù trò quan saùt cho thaáy moät quan heä ñöôøng cong (Xem Hình 3.11). Chuùng ta cuõng chæ ra
raèng coù hieän töôïng treã giöõa chi tieâu thöïc cho hoaït ñoäng nghieân cöùu vaø phaùt trieån vaø hieäu quaû
cuûa caùc chi tieâu naøy veà maët soá baèng saùng cheá. ÔÛ ñaây chuùng ta seõ öôùc löôïng moâ hình phi tuyeán
ñoäng vaø so saùnh caùc keát quaû. Tuy nhieân, vì chöa coù lyù thuyeát veà kinh teá hay caùc lyù thuyeát
khaùc veà soá naêm cuûa hieän töôïng treã naøy hoaëc veà daïng haøm soá caàn söû duïng, neân moät caùch tuøy yù
chuùng ta cho ñoä treã naøy leân ñeán 4 naêm. Boán bieán treã ñöôïc taïo ra goàm R&D(t-1), R&D(t-2),
R&D(t-3), vaø R&D(t-4). Caùc bieán naøy sau ñoù seõ ñöôïc bình phöông leân vaø moät moâ hình baäc
hai vôùi taát caû caùc bieán ñöôïc öôùc löôïng.

Hình 6.7 So Saùnh Moâ Hình Ñoäng vaø Moâ Hình Tónh (ñöôøng lieàn laø moâ hình tónh, x laø
giaù trò quan saùt thöïc, vaø o laø moâ hình ñoäng)

Soá baèng saùng cheá

Chi phí R&D

Vì vaäy, ñaây laø moät baøi taäp “khôùp ñöôøng cong” thuaàn tuùy thay vì laø moät baøi taäp döïa treân lyù
thuyeát kinh teá. Baùo caùo coù chuù giaûi in ra töø maùy tính ôû baûng 6.2 caàn ñöôïc tìm hieåu kyõ löôõng
(xem Phaàn Thöïc Haønh Maùy Tính 6.6 ñeå chaïy laïi baûng 6.2). Hình 6.7 veõ soá baèng saùng cheá
thaät, caùc giaù trò gaùn töø moâ hình tónh ôû Chöông 3 (ñöôøng thaúng lieàn), vaø caùc giaù trò töø moâ hình
ñoäng cuoái cuøng. Chuùng ta nhaän thaáy raèng moâ hình ñoäng theå hieän raát toát dieãn bieán thöïc teá,
ngay caû trong nhöõng naêm caùc chi phí R&D tuïm laïi vaø trong nhöõng naêm töø 1988-1993 khi moâ
hình tuyeán tính hoaøn toaøn khoâng theå hieän ñöôïc. Do ñoù moâ hình phi tuyeán ñoäng laø moät ñaëc
tröng toát hôn so vôùi moâ hình tónh tuyeán tính ñôn giaûn.

Baûng 6.2 Keát Quaû Maùy Tính Coù Keøm Chuù Giaûi Cho Phaàn Öùng Duïng ôû Phaàn 6.7



MODEL 1: OLS estimates using the 34 observations 1960-1993
Dependent variable: PATENTS

VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t>|T|)
0) const 34.5711 6.3579 5.438 0.000006 ***
3) R&D 0.7919 0.0567 13.966 0.000000 ***

Mean of dep. var. 119.238 S.D. of dep. variable 29.306
Error Sum of Sq (ESS) 3994.3003 Std Err of Resid. (sgmahat) 11.1724
Unadjusted R-squared 0.859 Adjusted R-squared 0.855
F-statistic (1, 32) 195.055 p-value for F() 0.000000
Durbin-Watson stat. 0.234 First-order autocorr. coeff 0.945

MODEL SELECTION STATISTICS

SGMASQ 124.822 AIC 132.146 FPE 132.164
HQ 136.255 SCHWARZ 144.56 SHIBATA 131.301
GCV 132.623 RICE 133.143
Baûng 6.2 (tieáp theo)

[phaùt caùc bieán treã]
R&D1 = R&D(-1) sq_R&D = (R&D)2
R&D2 = R&D(-2) sq_R&Di = (R&Di)2
R&D3 = R&D(-3) for I = 1,2,3, and 4
R&D4 = R&D(-4)

[Öôùc löôïng moâ hình toång quaùt vôùi taát caû caùc bieán giaûi thích baèng caùch söû duïng chæ caùc quan saùt töø 1964-
1993, vì caùc bieán treã khoâng ñöôïc ñònh nghóa trong giai ñoaïn töø 1960-1963]

MODEL 2: OLS estimates using 30 observations 1964-1993
Depedent variable: PATENTS

0) const 85.3526 22.1027 3.862 0.001051 ***
3) R&D -0.0477 1.1251 -0.042 0.966638
4) R&D1 0.6033 2.0562 0.293 0.772387
5) R&D2 0.0001794 2.1850 0.000 0.999935
6) R&D3 -0.5869 2.0522 -0.286 0.777989
7) R&D4 -0.1837 1.0994 -0.167 0.869055
8) sq_R&D -0.0007326 0.0049 -0.150 0.882674
9) sq_R&D1 -0.0018 0.0089 -0.197 0.845884
10) sq_R&D2 0.0017 0.0098 0.177 0.861555
11) sq_R&D3 -0.0007564 0.0092 -0.082 0.935597
12) sq_R&D4 0.0071 0.0051 1.405 0.176209






SGMASQ 11.7568 AIC 15.5026 FPE 16.0676
GCV 18.5633 RICE 27.9224

Excluding the constant, p-value was highest for variable 5 (R&D2)

[Löu yù raèng coù hieän töôïng ña coäng tuyeán raát cao giöõa caùc bieán giaûi thích. Caùc giaù trò hieän haønh vaø treã
cuûa chi phí R&D cuõng nhö R&D vaø caùc bình phöông cuûa chuùng ñöôïc kyø voïng laø töông quan chaët vôùi
nhau. Nhö vaäy, khoâng coù gì ngaïc nhieân, tröø soá haïng haèng soá, taát caû ñeàu khoâng coù yù nghóa. Nhö ñaõ ñeà
caäp ôû chöông tröôùc, ñieàu naøy khoâng coù nghóa raèng caùc bieán naøy laø “khoâng quan troïng”, maø chæ coù nghóa
raèng hieän töôïng ña coäng tuyeán coù theå laø nhöõng bieán aån caàn ñöôïc ñöa vaøo moâ hình. Theo phöông phaùp
ñôn giaûn hoùa moâ hình döïa treân döõ lieäu, chuùng ta neân loaïi caùc bieán thöøa. Böôùc ñaàu tieân, chuùng ta loaïi
boû caùc bieán vôùi giaù trò p-values treân 0,9. Ñoù laø caùc bieán R&D, R&D2, vaø sq_R&D3.]



0) const 84.8409 19.0579 4.452 0.000200 ***
4) R&D1 0.6043 0.6351 0.952 0.351669
6) R&D3 -0.7352 0.5233 -1.405 0.174012
7) R&D4 -0.0745 0.5134 -0.145 0.886004
8) sq_R&D -0.0009491 0.0012 -0.824 0.418554
9) sq_R&D1 -0.0017 0.0034 -0.496 0.624855
10) sq_R&D2 0.0016 0.0025 0.641 0.527835
12) sq_R&D4 0.0066 0.0020 3.364 0.002799 ***



SGMASQ 10.1647 AIC 12.7064 FPE 12.8753
GCV 13.861 RICE 15.9732



Excluding the constant, p-value was highest for variable 7 (R&D4).
Comparison of Model 2 and Model 3 is given below: Null hypothesis is: the regression parameters are zero for
the variables R&D, R&D2, and sq_R&D3.

Test statistic: F(3,19) = 0.006957, with p-value = 0.999173
Of the 8 model selection statistics, 8 have improved

[Trong kieåm ñònh F Wald cho caùc bieán bò loaïi ra, p-value ñaït giaù trò cao cho thaáy raèng chuùng ta khoâng
theå baùc boû giaû thuyeát khoâng cho raèng caùc heä soá cuûa caùc bieán naøy taát caû ñeàu baèng khoâng ngay caû taïi
möùc yù nghóa cao ñeán 0,9. Nhö vaäy, loaïi boû chuùng laø hôïp lyù. Hôn nöõa, taát caû taùm trò thoáng keâ choïn moâ
hình ñeàu giaûm, ñieàu ñoù coù nghóa coù moät söï caûi thieän veà ñoä thích hôïp cuûa moâ hình. Maëc duø nhieàu giaù
trò p-value giaûm, chæ coù duy nhaát moät giaù trò ñuû nhoû ñeå coù yù nghóa – ñoù laø giaù trò cuûa bieán soá 12. Ñieàu
naøy coù nghóa phaûi loaïi boû theâm. Tieáp theo, chuùng ta loaïi boû bieán R&D4, sq_R&D1, vaø sq_R&D2, caùc
bieán naøy öùng vôùi giaù trò p-value lôùn hôn 0,5]


0) const 82.8545 12.0355 6.884 0.000000 ***
4) R&D1 0.4771 0.3278 1.455 0.158001
6) R&D3 -0.6370 0.2388 -2.667 0.013227 **
8) Sq_R&D -0.0011 0.0010000 -1.146 0.262479
12) Sq_R&D4 0.0065 0.0006784 9.609 0.000000 ***




SGMASQ 9.34047 AIC 10.8631 FPE 10.8972
GCV 11.2086 RICE 11.6756

Excluding the constant, p-value was highest for variable 8 (sq_R&D).
Comparison of Model 3 and Model 4:

Null hypothesis is: the regression parameters are zero for the variables R&D4, sq_R&D1, and sq_R&D2.

Test statistic: F(3,22) = 0.324242, with p-value = 0.807788
Of the 8 model selection statistics, 8 have improved.



[Trong tröôøng hôïp naøy cuõng vaäy, trong kieåm ñònh F Wald cho caùc bieán bò loaïi ra, p-value ñaït giaù trò cao
cho thaáy raèng chuùng ta khoâng theå baùc boû giaû thuyeát khoâng cho raèng caùc heä soá cuûa caùc bieán naøy taát caû
ñeàu baèng khoâng ngay caû taïi möùc yù nghóa cao ñeán 0,8. Vì vaäy, vieäc loaïi boû chuùng laø hôïp lyù. Theâm nöõa,
taát caû taùm trò thoáng keâ choïn moâ hình ñeàu giaûm, ñieàu ñoù coù nghóa coù moät söï caûi thieän veà ñoä thích hôïp
cuûa moâ hình. Vaãn coøn hai bieán (sq_R&D vaø R&D1) coù giaù trò treân 15%. Chuùng ta tieáp tuïc loaïi boû caùc
bieán naøy, nhöng töøng bieán moät, vaø ñi ñeán moät moâ hình cuoái cuøng trong ñoù taát caû caùc heä soá coù yù nghóa ôû
möùc döôùi 2%]


0) const 91.3464 6.4046 14.263 0.000000 ***
6) R&D3 -0.2951 0.1175 -2.512 0.018286 **
12) sq_R&D4 0.0059 0.0005486 10.675 0.000000 ***



SGMASQ 9.58047 AIC 10.5315 FPE 10.5385
GCV 10.645 RICE 10.778
Of the 8 model selection statistics, 7 have improved.
[Tính caùc trò döï baùo vaø sai soá phaàn traêm tuyeät ñoái cho töøng döï baùo]

Obs R&D PATENT Predicted Prediction Absolute
S value error percent error

1964 76.83 93.2 93.1259 0.0740826 0.0794878
1965 80 100.4 93.8292 6.57081 6.54463
1966 84.82 93.5 94.8126 -1.31258 1.40383
1967 86.84 93 97.9126 -4.91264 5.28241
1968 88.81 98.7 102.306 -3.606 3.65394
1969 88.28 104.4 103.795 0.605085 0.579583
1970 85.29 109.4 107.851 1.5492 1.41609
1971 83.18 111.1 109.3 1.80002 1.62018
1972 85.07 105.3 111.483 -6.1826 5.87141
1973 86.72 109.6 111.815 -2.21525 2.02121
1974 85.45 107.4 109.399 -1.99891 1.86118



1975 83.41 108 106.76 1.24028 1.14841
1976 87.44 110 108.135 1.86509 1.69554
1977 90.11 109 110.169 -1.16945 1.07289
1978 94.5 109.3 109.491 -0.191014 0.174761
1979 99.28 108.9 106.285 2.61523 2.4015
1980 103.64 113 109.529 3.4713 3.07194
1981 108.77 114.5 111.009 3.49072 3.04867
1982 113.96 118.4 114.344 4.05551 3.42526
1983 121.72 112.4 118.482 -6.0819 5.41094
1984 133.33 120.6 122.149 -1.54888 1.28431
1985 144.78 127.1 126.998 0.101834 0.0801211
1986 148.39 133 131.477 1.52261 1.14482
1987 150.9 139.8 138.761 1.03908 0.743265
1988 154.36 151.9 152.722 -0.821732 0.540969
1989 157.19 166.3 170.303 -4.00303 2.40711
1990 161.86 176.7 175.76 0.9403 0.532145
1991 164.54 178.4 179.138 -0.737635 0.413472
1992 166.7 187.2 184.487 2.71267 1.44908
1993 165.2 189.4 188.272 1.12779 0.595455

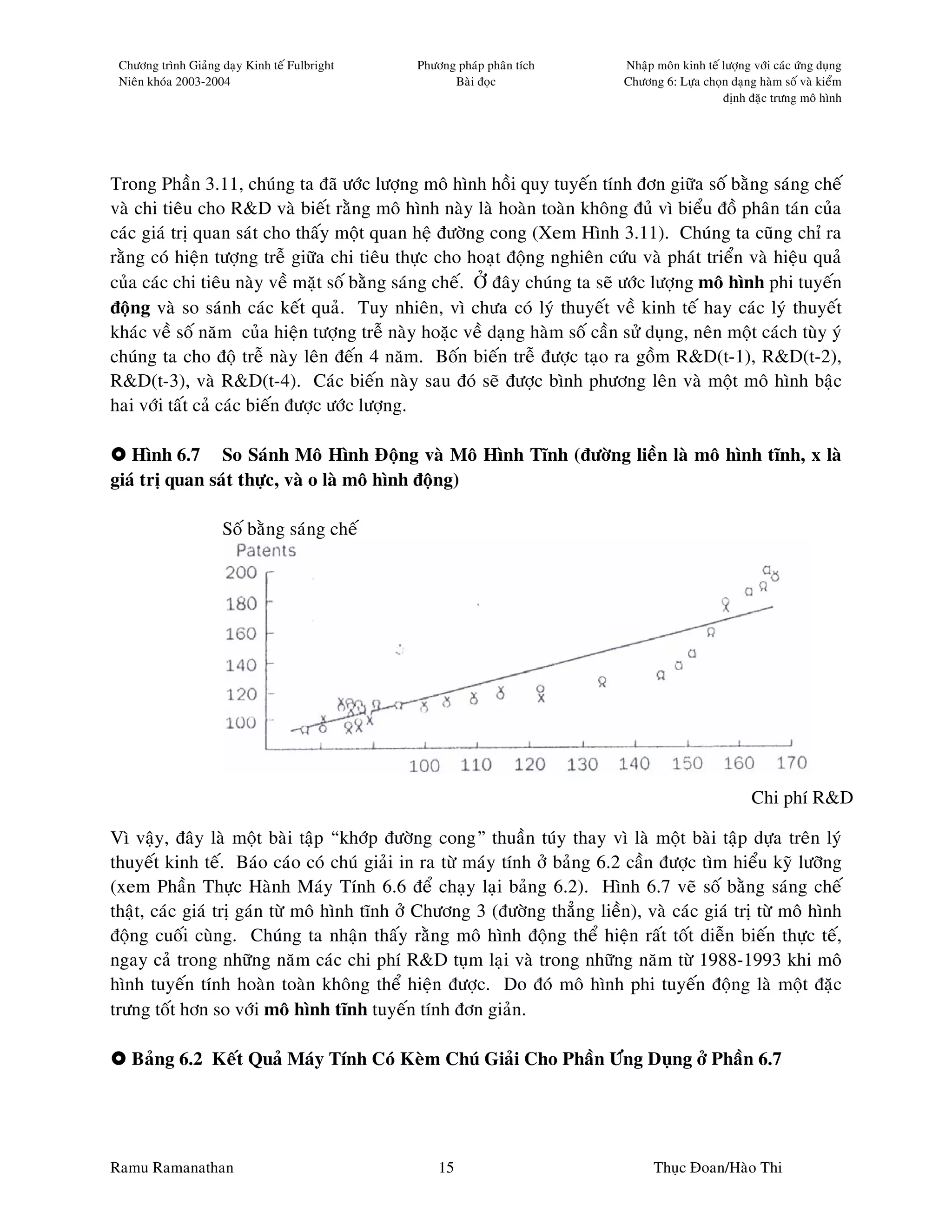
[Tröø moät soá naêm (1965, 1967, 1972 vaø 1983), taát caû caùc sai soá phaàn traêm tuyeät ñoái ñeàu nhoû hôn 5 phaàn
traêm. Thaät ra, haàu heát caùc giaù trò naøy ñeàu nhoû hôn 2 phaàn traêm. Cuõng nhö vaäy, so saùnh vôùi moâ hình
thoáng keâ tuyeán tính coù R bình phöông hieäu chænh baèng 0,855, moâ hình cuoái cuøng naøy coù giaù trò töông
öùng laø 0,988.]

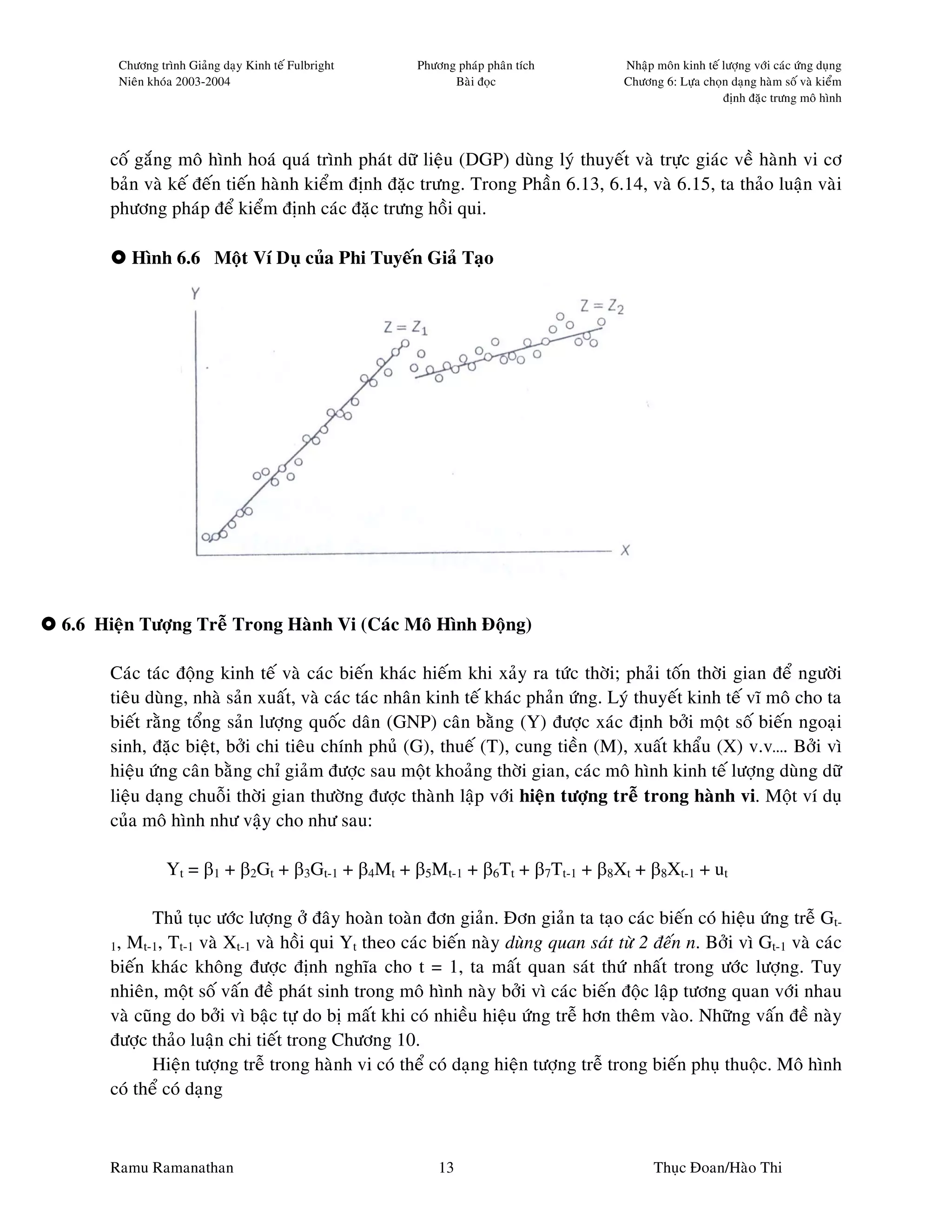
6.8 Quan heä tuyeán tính-logarit (hay laø moâ hình baùn logarit)

Taát caû caùc quan heä phi tuyeán ñöôïc thaûo luaän tröôùc ñaây coù bieán phuï thuoäc Y xuaát hieän döôùi
daïng tuyeán tính. Chæ coù nhöõng bieán ñoäc laäp phaûi traûi qua moïi söï bieán ñoåi. Cuõng seõ löu yù laø,
maëc duø chuùng ta söû duïng log vaø bình phöông cuûa caùc bieán ñoäc laäp, caùc moâ hình ñeàu tuyeán tính
theo caùc heä soá. Baây giôø, chuùng ta khaûo saùt moät vaøi moâ hình trong ñoù bieán ñoäc laäp xuaát hieän ôû
daïng bieán ñoåi.
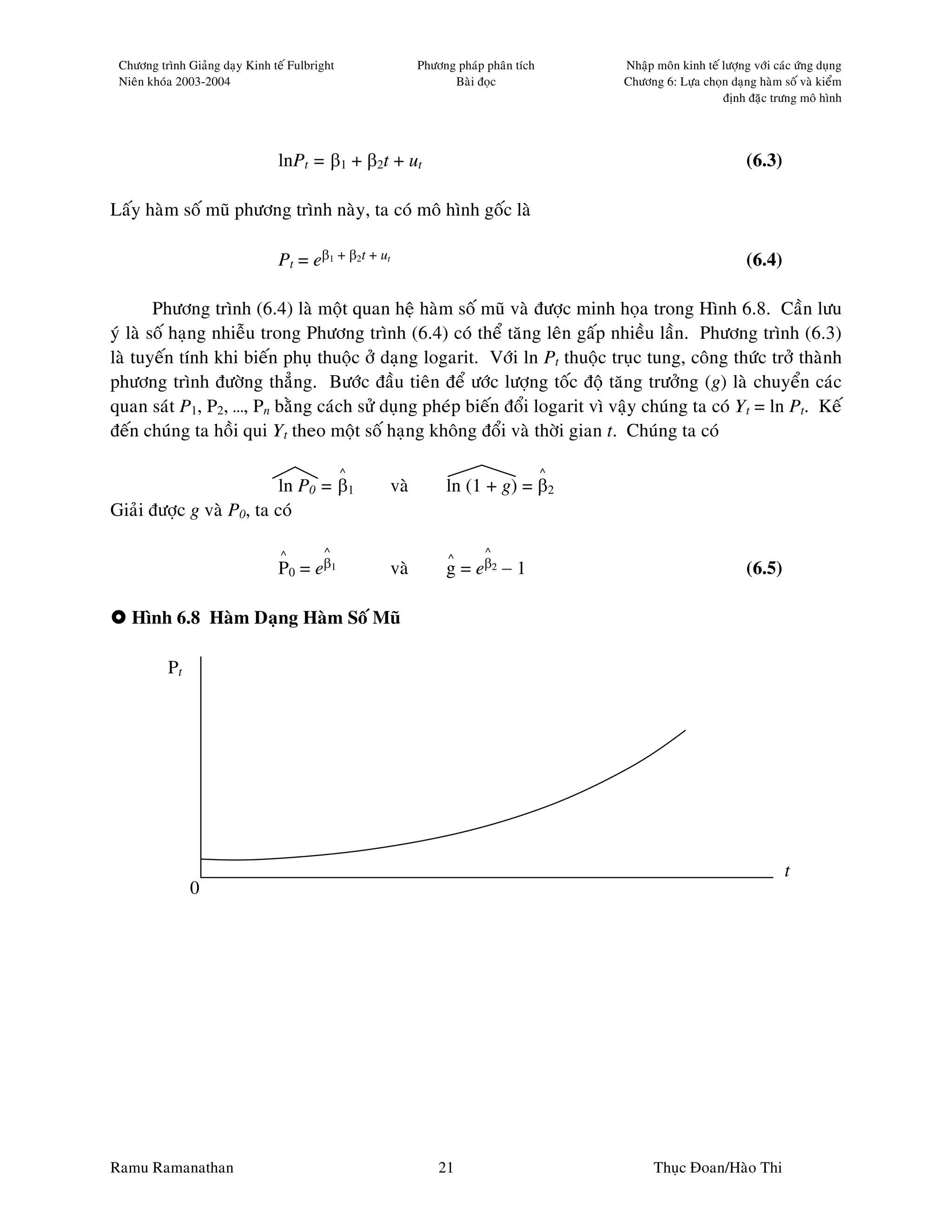
Giaû söû chuùng ta coù moät bieán P taêng vôùi moät toác ñoä khoâng ñoåi. Cuï theå hôn, ñaët Pt = (1 +
g)Pt – 1, vôùi g laø toác ñoä taêng tröôûng khoâng ñoåi giöõa thôøi ñoaïn t − 1 vaø t. P coù theå laø daân soá vaø g
laø toác ñoä taêng daân soá. Baèng caùch thay theá laëp laïi ta coù Pt = P0 (1+g)t. Söû duïng döõ lieäu veà Pt,
chuùng ta muoán öôùc löôïng toác ñoä taêng tröôûng g. Moái quan heä naøy khoâng coù daïng tuyeán tính
thuaän lôïi ñaõ ñöôïc duøng trong caùc phaàn tröôùc. Tuy nhieân, coù theå chuyeån quan heä naøy thaønh
daïng tuyeán tính ñöôïc. Laáy logarit cuûa hai veá (vaø duøng Tính chaát 6.1), chuùng ta coù lnPt = lnP0
+ t ln (1 + g). Ñaët Yt = lnPt, Xt = t, β1 = lnPo vaø β2 = ln (1 + g). Khi ñoù, moái quan heä coù theå
ñöôïc vieát laïi nhö sau Yt = β1 + β2Xt. Vì Y vaø X coù leõ khoâng thoûa maõn moät caùch chính xaùc moái
quan heä, chuùng ta coäng theâm moät soá haïng sai soá ut, laøm cho moái quan heä gioáng vôùi moâ hình
hoài qui ñôn giaûn cuûa Phöông trình (3.1). Moâ hình bieán ñoåi trôû thaønh



lnPt = β1 + β2t + ut (6.3)

Laáy haøm soá muõ phöông trình naøy, ta coù moâ hình goác laø

Pt = eβ1 + β2t + ut (6.4)

Phöông trình (6.4) laø moät quan heä haøm soá muõ vaø ñöôïc minh hoïa trong Hình 6.8. Caàn löu
yù laø soá haïng nhieãu trong Phöông trình (6.4) coù theå taêng leân gaáp nhieàu laàn. Phöông trình (6.3)
laø tuyeán tính khi bieán phuï thuoäc ôû daïng logarit. Vôùi ln Pt thuoäc truïc tung, coâng thöùc trôû thaønh
phöông trình ñöôøng thaúng. Böôùc ñaàu tieân ñeå öôùc löôïng toác ñoä taêng tröôûng (g) laø chuyeån caùc
quan saùt P1, P2, …, Pn baèng caùch söû duïng pheùp bieán ñoåi logarit vì vaäy chuùng ta coù Yt = ln Pt. Keá
ñeán chuùng ta hoài qui Yt theo moät soá haïng khoâng ñoåi vaø thôøi gian t. Chuùng ta coù

^ ^
ln P0 = β1 vaø ln (1 + g) = β2
Giaûi ñöôïc g vaø P0, ta coù

^ ^ ^
^
P0 = eβ1 vaø g = eβ2 − 1 (6.5)

Hình 6.8 Haøm Daïng Haøm Soá Muõ

Pt

t
0



Baát kyø giaû thuyeát naøo veà g ñeàu coù theå theå hieän ( coù moät soá ngoaïi leä khoâng ñaùng keå) thaønh
moät giaû thuyeát töông ñöông theo β2. Do bieán phuï thuoäc ñöôïc bieán ñoåi ôû daïng log, moâ hình naøy
ñöôïc goïi laø moâ hình tuyeán tính-logarit, hoaëc ñoâi khi coøn goïi laø moâ hình baùn logarit. Neáu
moâ hình naøy ñöôïc vieát döôùi daïng ln Pt = β1 + β2 Xt + ut, β2 laø taùc ñoäng bieân teá cuûa X leân ln Pt
khoâng phaûi leân Pt. β2 ñöôïc goïi laø toác ñoä taêng tröôûng töùc thôøi. Laáy ñaïo haøm hai veá theo Xt
(xem Tính chaát 6.2 veà ñaïo haøm), ta coù

d(ln Pt) 1 dPt
β2 = = (6.6)
dXt Pt dXt

Soá haïng dPt/Pt coù theå ñöôïc dieãn dòch nhö laø thay ñoåi cuûa Pt chia cho Pt. Khi nhaân vôùi 100, β2
cho phaàn traêm thay ñoåi cuûa Pt treân moät ñôn vò thay ñoåi cuûa Xt. Ñeå tính ñoä co giaõn cuûa P theo X,
xem Baûng 6.1.
Laáy giaù trò kyø voïng cuûa hai veá phöông trình (6.4), ta coù

E(Pt) = eβ1 + β2t E(eut ) (6.7)

Coù theå thaáy laø E(eut ) = eσ /2 ≠ 1, vaø do ñoù neáu chuùng ta döï baùo Pt baèng caùch duøng bieåu thöùc
2

eβ1 + β2t, giaù trò döï ñoaùn seõ thieân leäch, khoâng nhaát quaùn vaø khoâng hieäu quaû. Bieåu thöùc phuø hôïp
trong tröôøng hôïp naøy laø

^ ^ ^ ^
Pt = exp[β1 + β2 t + (σ2/2)] (6.8)

^ ^
vôùi σ2 laø phöông sai maãu cuûa caùc soá haïng sai soá vaø exp laø haøm soá muõ. Pt laø moät öôùc löôïng
nhaát quaùn cuûa E(Pt).
^ ^

Caàn coù moät ñieàu chænh töông töï trong Phöông trình (6.5) vì E(eβ2) = eβ2 + [Var (β2)/2]. Do
ñoù, moät öôùc löôïng khoâng thieân leäch cuûa g ñöôïc tính bôûi

~ = exp[ ^ ^
g β2 − 1/2 Var (β2)] − 1

Coù theå coù ñöôïc moät khoaûng döï baùo hieäu chænh cuûa Pt. Tröôùc ñaây, chuùng ta ñaõ ñònh nghóa
^ ^
Yt = ln (Pt). Ñaët Yt laø döï baùo cuûa ln(Pt) trong moâ hình tuyeán tính logarit vaø st = s(Yt) laø sai soá
^
chuaån ñöôïc öôùc löôïng töông öùng. Vaäy, khoaûng tin caäy cuûa Yt laø Yt ± t*st, vôùi t* laø ñieåm treân
phaân phoái t sao cho P(t > t*) = moät nöûa cuûa möùc yù nghóa (tham khaûo Phaàn 3.9 veà caùc khoaûng
tin caäy cuûa döï baùo). Laáy haøm soá muõ (nghóa laø ngöôïc vôùi laáy log) vaø hieäu chænh ñeå thieân leäch
gioáng nhö trong Phöông trình (6.8), chuùng ta coù khoaûng tin caäy hieäu chænh cho vieäc döï baùo Pt



^ ^ ^
laø exp[Yt ± t*st + (σ2/2)], vôùi σ2 laø phöông sai maãu cuûa caùc soá haïng sai soá. Caàn chæ ra laø
^ ^
khoaûng tin caäy naøy seõ khoâng ñoái xöùng qua Pt = exp[Yt + (σ2/2)]. Tham khaûo Nelson (1973,
trang 161-165) ñeå thaûo luaän theâm veà caùc döï baùo ñieåm vaø caùc khoaûng tin caäy cuûa chuùng khi
bieán phuï thuoäc ñöôïc bieán ñoåi sang log.

VÍ DUÏ 6.5
Moâ hình tuyeán tính-logarit ñöôïc söû duïng roäng raõi trong lyù thuyeát veà voán nhaân löïc trong ñoù lyù
thuyeát cho raèng logarit cuûa thu nhaäp hoaëc löông ñöôïc söû duïng nhö laø moät bieán phuï thuoäc. Ñeå
phaùt trieån lyù thuyeát naøy, giaû söû laø tyû suaát lôïi nhuaän cuûa moät naêm hoïc taäp theâm laø r. Vaäy, ñoái
vôùi thôøi ñoaïn thöù nhaát, löông w1 = (1 + r)w0. Ñoái vôùi hai naêm hoïc taäp coâng thöùc naøy laø w2 =
(1+ r)2w0. Ñoái vôùi s naêm, chuùng ta coù ws = (1 + r)2 w0. Laáy logarit, chuùng ta coù (tham khaûo
Tính chaát 6.1c).

ln(ws) = s ln(1+ r) + ln(w0) = β1 + β2s

Vì vaäy chuùng ta coù moät quan heä tuyeán tính-logarit giöõa löông vaø soá naêm hoïc taäp. Cuõng
lyù luaän töông töï ñoái vôùi soá naêm kinh nghieäm. Tuoåi cuûa moät nhaân vieân coù veû nhö coù moät loaïi
taùc ñoäng khaùc. Chuùng ta kyø voïng thu nhaäp thaáp khi moät ngöôøi coøn treû, vaø löông seõ taêng khi
ngöôøi naøy tuoåi caøng lôùn hôn, nhöng thu nhaäp laïi giaûm sau khi veà höu. Töông quan daïng ñöôøng
cong loài naøy coù theå ñöôïc kieåm ñònh baèng moät coâng thöùc baäc hai vôùi AGE vaø AGE2. Ñeå toång
quaùt hoùa, chuùng ta coù theå muoán kieåm ñònh xem hoïc vaán vaø kinh nghieäm coù cuøng moät daïng taùc
ñoäng baäc hai khoâng. Vì vaäy, moät moâ hình toång quaùt coù daïng nhö sau:

ln(WAGE) = β1 + β2EDUC + β3EXPER + β4AGE
+ β5EDUC2 + β6EXPER2 + β7AGE2 + u (6.9)

DATA6-4 chöùa döõ lieäu veà löông thaùng, hoïc vaán tính baèng soá naêm sau lôùp taùm, kinh
nghieäm tính baèng soá naêm vaø tuoåi cuûa maãu goàm 49 caù nhaân. Tröôùc tieân chuùng ta öôùc löôïng moâ
hình tuyeán tính-logarit tröôùc ñoù nhöng laïi tìm ñöôïc moät soá caùc heä soá hoài qui tuyeán tính khoâng
coù yù nghóa. Nhö tröôùc ñaây, chuùng ta thöïc hieän vieäc ñôn giaûn hoùa taäp döõ lieäu baèng caùch loaïi boû
caùc bieán laàn löôït moãi laàn moät bieán (xem Baøi Thöïc haønh Maùy tính phaàn 6.7 ñeå tính laïi caùc keát
quaû naøy) ñeán khi caùc trò thoáng keâ choïn moâ hình trôû neân xaáu hôn. Caùc keát quaû moâ hình cuoái
cuøng ñöôïc trình baøy ôû ñaây vôùi trò thoáng keâ t trong daáu ngoaëc.

ln(WAGE) = 7,023 + 0,005 EDUC2 + 0,024 EXPER (6.10)
(76,0) (4,3) (3,9)
–
R2 = 0,33 d.f. = 46



Caû trình ñoä hoïc vaán bình phöông vaø kinh nghieäm ñeàu raát coù yù nghóa ôû möùc döôùi 0,001. YÙ
nghóa cuûa heä soá kinh nghieäm 0,024 laø, giöõa hai nhaân vieân coù cuøng trình ñoä hoïc vaán, neáu ngöôøi
naøo coù nhieàu hôn moät naêm kinh nghieäm so vôùi ngöôøi coøn laïi thì seõ ñöôïc kyø voïng laø coù löông
cao hôn, trung bình khoaûng 2,4 phaàn traêm (xem Phöông trình 6.6 cho phaàn dieãn dòch naøy).
Löu yù laø EDUC coù taùc ñoäng baäc hai vôùi taùc ñoäng bieân teá taêng theo trình ñoä hoïc vaán. Tuy
nhieân, khoâng neân quaù xem troïng caùc keát quaû naøy vì pheùp ño ñoä thích hôïp khaù thaáp ngay caû ñoái
vôùi taäp döõ lieäu cheùo. Roõ raøng caàn thöïc hieän nhieàu coâng vieäc nöõa tröôùc khi chuùng ta coù ñöôïc
nhöõng con soá chính xaùc. Chuùng ta seõ nhaéc laïi moâ hình naøy trong nhöõng chöông sau vaø seõ coù
nhieàu keát quaû ñaùng tin caäy hôn.

Tansel (1994) coù moät öùng duïng roäng raõi moâ hình löông daïng logarit. Vì vaäy caàn nghieân
cöùu moâ hình naøy caån thaän.

BAØI TAÄP THÖÏC HAØNH 6.8
Söû duïng döõ lieäu trong DATA6-4, öôùc löôïng caû moâ hình toång quaùt trong Phöông trình (6.9) vaø
moâ hình cuoái cuøng trong Phöông trình (6.10). Thöïc hieän moät kieåm ñònh Wald söû duïng hai moâ
hình naøy. Haõy phaùt bieåu giaû thuyeát khoâng vaø giaû thuyeát ngöôïc laïi vaø keát luaän cuûa baïn döôùi
daïng vaên vieát.
Giaû söû löông ñöôïc tính baèng haøng traêm ñoâla. Vieäc naøy seõ aûnh höôûng ñeán caùc heä soá hoài
qui nhö theá naøo? Neáu coù baát kyø heä soá naøo thay ñoåi, haõy vieát laïi caùc giaù trò môùi trong Phöông
trình (6.10)

Tính taùc ñoäng bieân teá (dY/dX) vaø ñoä co giaõn (X/Y)(dX/dY) cuûa moâ hình lnY = β1 + β2X + β3X2
+u

Tính taùc ñoäng bieân teá vaø ñoä co giaõn cho moâ hình lnY = β1 + β2X + β3(XZ) + u.

Xeùt moâ hình tuyeán tính logarit lnY = β1 + β2X + β3Z + β4X2 + β5XZ + u, vôùi X vaø Z laø caùc bieán
giaûi thích. Tìm moät bieåu thöùc ñaïi soá cuûa ñoä co giaõn cuûa Y theo X. Haõy trình baøy caùch baïn söû
duïng kieåm ñònh Wald ñeå kieåm tra xem caùc soá haïng phi tuyeán X2 vaø XZ coù yù nghóa thoáng keâ
hay khoâng.

6.9 So Saùnh Caùc Giaù Trò R2 Giöõa Caùc Moâ Hình



Trong Ví duï 6.5, neáu chuùng ta ñaõ söû duïng WAGES nhö bieán phuï thuoäc thay vì logarit cuûa bieán
naøy, R2 hieäu chænh seõ laø 0,338. Vì R2 cuûa moâ hình tuyeán tính-logarit laø 0,333, nhö vaäy coù phaûi
laø moâ hình tuyeán tính ít nhieàu toát hôn veà möùc ñoä thích hôïp? Caâu traû lôøi laø chaéc chaén khoâng,
bôûi vì thaät laø khoâng ñuùng khi so saùnh caùc giaù trò R2 khi maø caùc bieán phuï thuoäc laø khaùc nhau.
Trong tröôøng hôïp tuyeán tính, moâ hình giaûi thích 33,8 phaàn traêm thay ñoåi cuûa Y, trong khi trong
tröôøng hôïp tuyeán tính-logarit, moâ hình giaûi thích 33,3 phaàn traêm thay ñoåi trong ln(Y). Ñeå söï
so saùnh laø hôïp lyù, caùc bieán phuï thuoäc phaûi gioáng nhau.
Tuy nhieân, coù moät caùch so saùnh ñoä thích hôïp baèng caùch thöû sai. Caùc bieán trong tröôøng hôïp
tuyeán tính-logarit nhö sau:
Böôùc 1 Öôùc löôïng moâ hình tuyeán tính-logarit nhö caùch laøm thoâng thöôøng vaø tính ñöôïc giaù trò
thích hôïp cho moâ hình ln(Y).
Böôùc 2 Töø nhöõng giaù trò naøy, taïo giaù trò trung bình öôùc löôïng cho Y baèng caùch pheùp tính
nghòch cuûa logarit, vaø baûo ñaûm laø thieân leäch hieäu chænh nhö trong Phöông trình (6.8).
Vaäy, chuùng ta seõ coù

^ ^
Yt = exp[ln(Yt) + (σ2/2)] (6.11)

^
Böôùc 3 Tính bình phöông cuûa töông quan giöõa Yt vaø Yt. Töông quan naøy coù theå so saùnh ñöôïc
vôùi R2 hieäu chænh cuûa moät moâ hình tuyeán tính.
Böôùc 4 Tính toång bình phöông sai soá vaø phöông sai cuûa phaàn dö baèng caùch söû duïng caùc moái
quan heä

^ ESS ^
ESS = ∑(Yt – Yt)2 vaø σ2 =
n–k
Böôùc 5 Duøng ESS, tính caùc trò thoáng keâ löïa choïn moâ hình ñoái vôùi moâ hình môùi. Caùc trò thoáng
keâ naøy coù theå so saùnh ñöôïc vôùi caùc trò thoáng keâ cuûa moâ hình tuyeán tính.

VÍ DUÏ 6.6
Söû duïng döõ lieäu trong DATA6-4 vaø moâ hình tuyeán tính-logarit ñöôïc öôùc löôïng trong Ví duï 6.5,
chuùng ta ñaõ tieán haønh caùc böôùc naøy vaø ñaõ tính ñaïi löôïng R2 môùi vaø caùc trò thoáng keâ löïa choïn
moâ hình (xem chi tieát trong Baøi thöïc haønh maùy tính 6.8). Keát quaû tìm ñöôïc laø R2 baèng 0,37,
lôùn hôn raát nhieàu so vôùi giaù trò naøy trong moâ hình tuyeán tính. Taát caû caùc trò thoáng keâ löïa choïn
moâ hình cuûa moâ hình tuyeán tính-logarit ñeàu thaáp hôn so vôùi moâ hình tuyeán tính. Vì vaäy, theo
caùc tieâu chuaån naøy, moâ hình tuyeán tính-logarit coù öu theá hôn moät chuùt.

6.10 Moâ hình Log-hai laàn (hay Log-Log)



Moâ hình Log-hai laàn (hay Log-Log) raát phoå bieán trong öôùc löôïng caùc haøm saûn xuaát cuõng nhö
haøm nhu caàu. Neáu Q laø soá löôïng ñaàu ra cuûa moät quaù trình saûn xuaát, K laø soá löôïng voán ñaàu vaøo
(soá giôø maùy), vaø L laø soá löôïng lao ñoäng ñaàu vaøo (soá giôø nhaân coâng lao ñoäng), thì töông quan
giöõa ñaàu ra vaø ñaàu vaøo laø phöông trình haøm saûn xuaát vieát nhö sau Q = F(K,L). Moät ñaëc tröng
chung cuûa daïng haøm naøy laø haøm saûn xuaát Cobb-Douglas, raát noåi tieáng trong lyù thuyeát kinh teá
vi moâ. Haøm naøy coù daïng toång quaùt sau:
Qt = cKtαLtβ

vôùi c, α vaø β laø nhöõng thoâng soá chöa bieát. Laáy logarit hai veá (xem Tính chaát 6.1) vaø theâm vaøo
soá haïng sai soá, chuùng ta coù ñöôïc haøm kinh teá löôïng (β1 = ln c):

ln Qt = β1 + α ln Kt + β ln Lt + ut

Neáu chuùng ta chæ thay ñoåi K nhöng giöõ L khoâng ñoåi, thì chuùng ta coù (söû duïng Tính chaát 6.2c)
∆ (ln Q) (1/Q) ∆Q K ∆Q
α= = =
∆ (ln K) (1/K) ∆K Q ∆K

100∆(lnQ) = 100∆Q/Q laø phaàn traêm thay ñoåi theo Q. Do ñoù, α laø phaàn traêm thay ñoåi cuûa Q
chia cho phaàn traêm thay ñoåi cuûa K. Ñaây laø ñoä co giaõn cuûa ñaàu ra theo voán. Töông töï nhö
vaäy, β laø ñoä co giaõn cuûa ñaàu ra theo lao ñoäng. Vì vaäy, caùc heä soá hoài qui trong moâ hình log-
hai laàn ñôn giaûn laø caùc ñoä co giaõn töông öùng, coù giaù trò khoâng ñoåi. Löu yù, vì tính chaát naøy, caùc
giaù trò baèng soá cuûa caùc heä soá cuûa caùc bieán ñoäc laäp khaùc nhau thì coù theå so saùnh ñöôïc tröïc tieáp.
Baûng 6.3 toùm taét dieãn dòch cuûa caùc heä soá hoài qui trong caùc moâ hình coù logarit cuûa caùc bieán.

Baûng 6.3 Dieãn dòch Caùc taùc ñoäng bieân teá trong caùc moâ hình lieân quan ñeán Logarit

Moâ hình Daïng haøm soá Taùc ñoäng bieân teá Dieãn dòch

Tuyeán tính Y = β 1 + β 2X ∆Y = β2∆X Moät ñôn vò thay ñoåi
trong X seõ laøm Y thay
ñoåi β2 ñôn vò
Logarit-tuyeán tính Y = β1 + β2lnX β2  ∆X Moät phaàn traêm thay
∆Y = 100 
100  X  ñoåi trong X seõ laøm Y
thay ñoåi β2/100 ñôn vò
Tuyeán tính-logarit lnY = β1 + β2X ∆X Moät ñôn vò thay ñoåi
100 = 100β2∆X
X trong X seõ laøm Y thay
ñoåi 100β2 phaàn traêm
logarit-hai laàn ln Y = β1 + β2ln X ∆Y Moät phaàn traêm thay
100 =
Y ñoåi trong X seõ laøm Y
thay ñoåi β2 phaàn traêm



 ∆X
β2100 
 X

Chuùng ta coù theå coù ñöôïc keát quaû thuù vò töø moâ hình naøy. Giaû söû soá löôïng voán vaø lao ñoäng
ñaàu vaøo taêng gaáp ñoâi. Luùc naøy ñaàu ra laø

Q1 = c(2K)α (2L)β = 2α+β Q

Neáu α + β = 1, Q1 = 2Q. Vì vaäy, ñaàu ra cuõng seõ taêng gaáp ñoâi neáu α + β = 1. Ñaây laø ñieàu
^ ^
kieän raát phoå bieán veà lôïi nhuaän khoâng ñoåi theo qui moâ. Neáu caùc ñoä co giaõn öôùc löôïng laø α + β
^ ^
> 1, chuùng theå hieän lôïi nhuaän taêng theo qui moâ, vaø α + β < 1 cho thaáy lôïi nhuaän giaûm theo
qui moâ. Moät kieåm ñònh thoâng thöôøng ñoái vôùi lôïi nhuaän khoâng ñoåi theo qui moâ raát thuù vò. Giaû
thuyeát khoâng laø H0: α + β = 1 vaø giaû thuyeát ñoái laø H1: α + β ≠ 1. Trong Phaàn 4.4, chuùng ta phaùt
trieån ba kieåm ñònh cho caùc giaû thuyeát lieân quan ñeán toå hôïp tuyeán tính cuûa caùc heä soá hoài qui.
Ñeå aùp duïng Phöông phaùp 2, ñònh nghóa β2 = α + β – 1. Theo giaû thuyeát khoâng, β2 = 0. Giaûi
ñöôïc β, chuùng ta coù β = β2 + 1 – α. Thay vaøo moâ hình, ta coù
lnQt = β1 + α lnKt + (β2 + 1 – α) lnLt + ut
= β1 + α (lnKt – lnLt) + lnLt + β2 lnLt + ut

Moâ hình naøy khoâng theå öôùc löôïng ñöôïc nhö daïng ôû treân vì soá haïng lnLt khoâng coù heä soá. Ñeå
öôùc löôïng, caùc bieán nhö vaäy phaûi ñöôïc chuyeån sang veá beân traùi. Vì vaäy, ta coù

LnQt – lnLt = β1 + α (lnKt – lnLt) + β2 lnLt + ut

Ñaët Yt = lnQt – lnLt, Xt1 = lnKt – lnLt, vaø Xt2 = lnLt, moâ hình trôû thaønh

Yt = β1 + αXt1 + β2Xt2 + ut

Ñeå öôùc löôïng moâ hình, chuùng ta bieán ñoåi caùc bieán ban ñaàu ñeå taïo ra caùc bieán môùi vaø sau ñoù
hoài qui Yt theo moät soá haïng khoâng ñoåi, Xt1 vaø Xt2. Kieåm ñònh caàn ñoái vôùi lôïi nhuaän khoâng ñoåi
theo qui moâ chæ ñôn giaûn laø moät kieåm ñònh t veà heä soá cuûa Xt2.

BAØI TAÄP THÖÏC HAØNH 6.12+
Moâ taû caùc böôùc thöïc hieän moät kieåm ñònh töông töï söû duïng Phöông phaùp 1 vaø 3 ñöôïc moâ taû
trong Phaàn 4.4

Giaû ñònh veà lôïi nhuaän khoâng ñoåi theo qui moâ vaãn ñöôïc giöõ; nghóa laø α + β = 1. Theo giaû thieát
naøy, haõy moâ taû baèng caùch naøo coù theå öôùc löôïng ñöôïc haøm saûn xuaát Cobb-Douglas.



Ví Duï Thöïc Nghieäm: Moät Haøm Saûn Xuaát Noâng Nghieäp
Carrasco-Tauber vaø Moffitt (1992) ñaõ öôùc löôïng moät haøm saûn xuaát loaïi Cobb-Douglas lieân heä
giaù trò cuûa saûn löôïng noâng nghieäp (ôû daïng log-hai laàn) vôùi lao ñoäng, ñaát, nhaø, maùy moùc thieát
bò, caùc ñaàu vaøo khaùc, phaân boùn vaø thuoác tröø saâu. Sau ñoù, hoï ñaõ söû duïng haøm saûn xuaát öôùc
löôïng ñeå tính saûn löôïng bieân teá aån (ñöôïc ñaùnh giaù baèng trung bình hình hoïc) cuûa moãi loaïi ñaàu
vaøo noâng nghieäp. Döõ lieäu naêm 1987 cuûa caùc tieåu bang ôû Myõ, tröø Alaska vaø Hawaii. Taát caû
caùc bieán tính baèng haøng ngaøn ñoâla moãi noâng traïi, tröø lao ñoäng tính baèng ngaøn ngaøy treân moãi
noâng traïi. Moâ hình öôùc löôïng ñöôïc cho ôû ñaây, vôùi caùc trò thoáng keâ t trong ngoaëc ñôn.

Ln Q = 4,461 + 0,227 ln(lao ñoäng) + 0,159 ln (ñaát & nhaø)
(2.11) (2,12) (2,01)
+ 0,274 ln(maùy moùc thieát bò) + 0,402 ln(caùc ñaàu vaøo khaùc)
(2,42) (8,55)
+ 0,082 ln(phaân boùn) + 0,136 ln (thuoác tröø saâu)
(0,85) (2,00)
Tröø ñoä co giaõn cuûa phaân boùn, caùc ñaàu vaøo khaùc coù yù nghóa thoáng keâ ôû möùc 5 phaàn traêm.
Caùc saûn phaåm bieân teá öôùc löôïng ñoái vôùi caùc ñaàu vaøo laø $44,54 moãi ngaøy ñoái vôùi lao ñoäng,
$0,04 cho moãi ñoâla ñaát vaø nhaø, $1,25 cho moãi ñoâla maùy moùc, $1,29 cho moãi ñoâla cuûa caùc ñaàu
vaøo khaùc, $4,91 cho moãi ñoâla phaân boùn vaø $5,66 cho moãi ñoâla thuoác tröø saâu. Caùc taùc giaû ñaõ
öôùc löôïng moät soá moâ hình thay theá baèng caùch söû duïng daïng haøm soá khoâng ñöôïc thaûo luaän
trong chöông naøy vaø ñaõ thu ñöôïc caùc ñaïi löôïng saûn löôïng bieân teá khaùc nhau ñoái vôùi moät soá ñaàu
vaøo. Caùc ñoäc giaû quan taâm coù theå tham khaûo chi tieát trong caùc baøi baùo cuûa nhöõng taùc giaû naøy.

6.11 ÖÙng Duïng: Öôùc Löôïng Ñoä Co Giaõn Cuûa Giao Thoâng Baèng Xe Buyùt

Vì moâ hình log-hai laàn cho caùc heä soá hoài qui coù ñoä co giaõn khoâng ñoåi, ñaây laø moät haøm raát
thoâng duïng trong öôùc löôïng haøm nhu caàu. Chuùng ta minh hoïa moâ hình log-hai laàn baèng caùch
xem laïi caùc yeáu toá quyeát ñònh cuûa giao thoâng baèng xe buyùt ñaõ tìm hieåu trong Phaàn 4.6. Taäp döõ
lieäu trong taäp tin DATA4-4, vaø Baøi thöïc haønh maùy tính Phaàn 6.9 coù höôùng daãn ñeå tính toaùn caùc
keát quaû ñöôïc trình baøy ôû ñaây.

Moâ hình cuøng vôùi taát caû caùc bieán giaûi thích seõ coù heä soá khoâng yù nghóa (ôû möùc 10%) ñoái vôùi
logarit cuûa FARE, GASPRICE, POP, DENSITY, vaø LAND AREA, trong ñoù log cuûa haøm maät
ñoä daân soá ít coù yù nghóa nhaát (nghóa laø coù giaù trò p cao nhaát). Khi bieán naøy ñöôïc loaïi boû ra ngoaøi
vaø moâ hình ñöôïc öôùc löôïng laïi thì heä soá ñoái vôùi haøm INCOME, POP, vaø LANDAREA trôû neân
coù yù nghóa ôû möùc döôùi 0,001. Nguyeân nhaân chuû yeáu veà maët lyù thuyeát cho söï thay ñoåi nghieâm
troïng naøy laø do giaûm tính ña coäng tuyeán vaø laøm taêng baäc töï do keát hôïp vôùi moät moâ hình nhoû
goïn hôn coù theå caûi thieän ñöôïc ñoä chính xaùc cuûa caùc heä soá. Chuùng ta tieáp tuïc loaïi bôùt nhöõng
bieán khaùc maø heä soá cuûa chuùng khoâng coù yù nghóa cho ñeán khi chæ coøn laïi nhöõng heä soá coù yù



nghóa maø thoâi. Nhö trong tröôøng hôïp tuyeán tính, ln(FARE) cuõng bò loaïi boû. Moâ hình sau ñaây laø
moâ hình cuoái cuøng vôùi sai soá chuaån ñeå trong ngoaëc ñôn (khoâng gioáng nhö trò thoáng keâ t thoâng
thöôøng):

ln(BUSTRAVL) = 45,846 – 4,730 ln(INCOME) + 1,820 ln(POP)
(9,614) (1,021) (0,236)

– 0,971 ln(LANDAREA)
(0,207)
R = 0,609
2
d.f = 36

Moät caâu hoûi thuù vò khaùc ñöôïc neâu ra laø bieán du lòch baèng xe buyùt coù tính chaát co giaõn hay
khoâng co giaõn. Neáu giaù trò baèng soá cuûa ñoä co giaõn naøy thaáp hôn 1 (boû qua daáu) thì chuùng ta coù
theå keát luaän raèng bieán söû duïng xe buyùt laø khoâng co giaõn. Neáu noù cao hôn 1 thì coù nghóa laø bieán
coù tính co giaõn. Giaû thuyeát khoâng chính thöùc seõ ñöôïc aùp duïng ñoái vôùi heä soá naøy vaø giaû thuyeát
ngöôïc laïi seõ coù tính hai phía. Trò thoáng keâ kieåm ñònh ñoái vôùi moãi bieán co giaõn laø

4.73 – 1 1.82 – 1 0.971 – 1
= 3.65 = 3.47 = – 0.14
1.021 0.236 0.207

Töø baûng tra t ñöôïc trình baøy ôû maët trong cuûa trang bìa ñaàu, chuùng ta coù giaù trò tôùi haïn vôùi
baäc töï do 36 vaø möùc yù nghóa 0,002 (ñoái vôùi kieåm ñònh hai phía) naèm giöõa 3,307 vaø 3,385. Vì trò
thoáng keâ t ñoái vôùi heä soá cuûa bieán thu nhaäp vaø daân soá tính toaùn ñöôïc cao hôn khoaûng naøy neân
chuùng ta coù theå keát luaän raèng tính co giaõn cuûa caùc bieán soá treân laø coù yù nghóa. Tuy nhieân, ngöôïc
laïi thì heä soá ñoái vôùi bieán dieän tích ñaát laø khoâng khaùc 1, ngay caû vôùi möùc 0,8 (giaù trò tôùi haïn
naèm trong khoaûng 0,225 vaø 0,256 vaø giaù trò baèng soá cao hôn giaù trò quan saùt ñöôïc). Trong
tröôøng hôïp naøy, chuùng ta coù theå keát luaän raèng bieán dieän tích ñaát coù tính chaát co giaõn ñôn vò.

Thöïc hieän kieåm ñònh Wald töông töï nhö baøi taäp thöïc haønh 6.8

6.12 Nhöõng Moâ Hình Khaùc *

Moâ Hình Logit *
Trong vaøi tröôøng hôïp, bieán phuï thuoäc coù theå nhaän giaù trò giöõa 0 vaø 1. Ví duï ta coù theå lieân heä
giöõa phaân soá cuûa soá ngöôøi boû phieáu cho moät vò toång thoáng naøo ñoù vôùi caùc yeáu toá quyeát ñònh
cuûa noù. Moät caùch khaùc, coù theå lieân heä giöõa phaân soá cuûa soá ngöôøi mua xe hôi trong moät thôøi
ñoaïn xaùc ñònh naøo ñoù vôùi caùc yeáu toá quyeát ñònh cuûa noù. Neáu moät moâ hình hoài quy thoâng
thöôøng naøo ñoù ñöôïc söû duïng trong nhöõng tröôøng hôïp nhö vaäy thì khoâng coù gì coù theå baûo ñaûm



raèng giaù trò döï ñoaùn tröôùc seõ naèm trong khoaûng 0 vaø 1. Ñeå baûo ñaûm khoâng xaûy ra nhöõng tröôøng
hôïp nhö vaäy, ngöôøi ta thöôøng aùp duïng moät daïng haøm nhö sau (ñöôïc goïi laø ñöôøng cong
Logistic):

 P 
ln   = α + βX + u
1 − P 

trong ñoù P giaù trò cuûa bieán phuï thuoäc naèm trong khoaûng 0 vaø 1. Moâ hình naøy thöôøng ñöôïc goïi
laø moâ hình Logit. Ruùt P töø phöông trình treân (baèng caùch laáy haøm soá muõ laàn thöù nhaát hai veá
phöông trình), ta coù

1
P= −( α +β X + u )
1+ e

Deã daøng nhaän thaáy raèng, neáu giaù trò β > 0 thì P seõ tieán ñeán giaù trò 0 khi X → -∞, vaø giaù trò
1 khi X → ∞. Vì theá, giaù trò P khoâng bao giôø vöôït ra khoûi phaïm vi [0, 1]. Ñöôøng cong Logistic
seõ coù hình daùng nhö trình baøy trong hình 6.9. Ñöôøng cong naøy cuõng ñöôïc söû duïng ñeå khôùp vôùi
daïng ñöôøng cong taêng tröôûng. Ví duï, doanh soá baùn haøng cuûa moät saûn phaåm môùi (nhö tivi coù ñoä
neùt cao) coù theå taêng nhanh trong thôøi gian ñaàu nhöng sau ñoù giaûm daàn roài ngöng haún. Moâ hình
Logit ñöôïc öôùc löôïng döïa treân caùch tính hoài quy cuûa haøm ln[P/(1 - P)] theo moät haèng soá vaø
bieán X.
Nhöõng moâ hình döôùi daïng nhö vaäy ñöôïc môû roäng vaø phaân tích ñaày ñuû hôn ôû chöông 12.

Pheùp bieán ñoåi Box – Cox *
Trong moâ hình sau ñaây, ngöôøi ta ñaõ söû duïng pheùp bieán ñoåi ñöôïc goïi pheùp bieán ñoåi Box – Cox
[xem Box and Cox (1964)]:

Yλ − 1 Xλ − 1
= α+β +u
λ λ

Hình 6.9 Ñoà Thò Ñöôøng Cong Logistic

Y

1

Ramu Ramanathan
X c Ñoan/Haøo Thi
0 30 Thuï


Coù theå chöùng minh ñöôïc raèng khi giaù trò λ = 0 thì moâ hình coù theå ruùt goïn baèng daïng log – hai
laàn ln Y = α + β ln X + u. Trong tröôøng hôïp λ = 1, chuùng ta coù ñöôïc moâ hình daïng tuyeán tính Y
– 1 = α + β (X - 1) + u hay Y = α* + βX + u, trong ñoù α* = α - β + 1. Khi λ nhaän caùc giaù trò
khaùc, chuùng ta seõ coù ñöôïc moâ hình phi tuyeán tính. Moâ hình naøy coù theå öôùc löôïng baèng thuû tuïc
öôùc löôïng thích hôïp nhaát baèng caùch söû duïng chöông trình toái öu hoaù phi tuyeán tính. Ñoà thò haøm
soá seõ coù nhieàu daïng moät caùch linh ñoäng, vaø ngöôøi ta coù theå kieåm ñònh vôùi λ baèng 0 hay baèng 1,
hay vôùi caùc giaù trò khaùc. Neáu bieát tröôùc ñöôïc phaïm vi giaù trò cuûa λ töø –1 ñeán +1, chuùng ta coù
theå choïn moät giaù trò cho λ vaø daïng caùc bieán môùi laø Y* = (Yλ – 1)/λ vaø X* = (Xλ – 1)/λ. Sau ñoù
chuùng ta hoài quy Y* theo bieán X* vaø theo caùc soá haïng haèng soá vaø nhaän ñöôïc toång bình phöông
sai soá. Chuùng ta laäp laïi quy trình naøy vôùi caùc giaù trò khaùc nhau cuûa λ vaø choïn ra giaù trò nhoû
nhaát trong soá caùc keát quaû toång bình phöông sai soá. Quy trình doø tìm naøy coù theå thöïc hieän baèng
chöông trình hoài quy tuyeán tính maø khoâng caàn ñeán chöông trình hoài quy phi tuyeán tính. Phaàn
môû roäng cho phöông phaùp naøy laø söû duïng ñaúng thöùc X* = (Xµ – 1)/µ, thöû keát quaû vôùi caùc giaù trò
λ vaø µ (töø -1 ñeán +1), vaø choïn ra toå hôïp maø cho keát quaû toång bình phöông sai soá ESS laø nhoû
nhaát.
Muoán bieát theâm chi tieát veà pheùp bieán ñoåi Box – Cox, xin tham khaûo taùc giaû Kim vaø Hill
(1993), Showalter (1994) vaø taùc giaû Wooldridge (1992).

Tính Phi Tuyeán Trong Caùc Thoâng Soá *
Chuùng ta ñaõ xem xeùt nhieàu phöông phaùp maø trong ñoù tính chaát phi tuyeán trong caùc bieán coù theå
giaûi quyeát töông töï nhö trong tröôøng hôïp hoài quy tuyeán tính, töùc laø caùc bieán naøy seõ ñöôïc bieán
ñoåi moät caùch thích hôïp, vaø nhö vaäy chuùng ta seõ coù ñöôïc moät moâ hình tuyeán tính vôùi heä soá hoài
quy chöa bieát. Tuy nhieân, cuõng coù nhöõng tröôøng hôïp maø caùch thöùc treân khoâng theå thöïc hieän
ñöôïc. Haøm Box – Cox laø moät ví duï cho tröôøng hôïp maø moái quan heä laø phi tuyeán tính trong caùc
thoâng soá vaø cuõng khoâng theå bieán ñoåi thaønh daïnh tuyeán tính ngoaïi tröø moät vaøi tröôøng ñaëc bieät
keå treân. Moät ví duï khaùc laø haøm saûn xuaát cuûa caùc bieán thay theá coù heä soá co giaõn khoâng ñoåi
(CES), ñöôïc cho nhö sau:

Q = γ [δ K– ρ + (1 - δ) L– ρ] – ν / ρ eu (γ > 0, 0 < δ < 1, ν > 0, ρ ≥ -1)

Trong ñoù thoâng soá chöa bieát γ, δ, ν, vaø ρ coù tính chaát phi tuyeán. Chuùng chæ coù theå xaùc ñònh
baèng thuû tuïc öôùc löôïng thích hôïp nhaát hoaëc baèng caùc phöông phaùp bình phöông toái thieåu phi
tuyeán. Tuy nhieân, trong tröôøng hôïp naøy taùc giaû Kmenta (1986, trang 515) ñaõ aùp duïng caùch tính
bình phöông baäc hai gaàn ñuùng nhö sau:



1
ln Q = ln γ + γδ ln K + ν(1 − δ) ln L − ρνδ(1 − δ)[ln K − ln L]2 + u
2
= β1 + β 2 ln K + β 3 ln L + β 4 (ln K − ln L) 2 + u

Giaù trò öôùc löôïng cuûa caùc thoâng soá ban ñaàu trong haøm saûn xuaát CES coù theå laáy keát quaû töø giaù
trò öôùc löôïng cuûa caùc β.
Maëc duø coù theå deã daøng bieán ñoåi caùc bieán vaø ñöa chuùng vaøo trong moâ hình nhöng neân
traùnh vieäc aùp duïng caùc phöông phaùp bieán ñoåi maø khoâng phaân bieät yù nghóa öùng duïng cuûa caùc
phöông phaùp naøy. Ñieàu caàn thieát laø haõy xem xeùt nhöõng ñieåm lyù thuyeát cô baûn trong caùc pheùp
bieán ñoåi vaø giöõ cho moâ hình caøng ñôn giaûn caøng toát.

6.13 Phöông Phaùp Moâ Hình Hoaù “Töø Toång Quaùt Ñeán Ñôn Giaûn” Hendry/Lse

Nhö ñaõ phaùt bieåu tröôùc ñaây, söï hình thaønh moâ hình kinh teá löôïng möùc chaáp nhaän ñöôïc laø raát
caàn thieát ñoái vôùi nhöõng keát luaän ruùt ra töø moâ hình ñoù. Trong caùc phaàn vaø chöông tröôùc, chuùng
ta ñaõ thaûo luaän veà nhöõng tieâu chuaån duøng ñeå ñaùnh giaù xem theá naøo laø moät moâ hình “toát”. Quaù
trình ñaàu tieân hình thaønh moâ hình ñöôïc döïa treân lyù thuyeát kinh teá. Ñaây laø nhöõng kieán thöùc
rieâng cuûa nhaø nghieân cöùu veà nhöõng haønh vi cô baûn, veà nhöõng nghieân cöùu khaùc töông töï, ...v.v.
Nhaø phaân tích cuõng coù theå coù nhöõng yù kieán toång quan veà caùc taùc ñoäng coù theå cuûa tính chaát phi
tuyeán cuõng nhö söï töông taùc giöõa caùc bieán. Vì khoâng theå coù moät phöông phaùp thoáng nhaát
chung trong vieäc xaùc ñònh moái quan heä giöõa bieán phuï thuoäc vaø bieán giaûi thích, neân nhaø nghieân
cöùu thöôøng ñöa ra caùc moâ hình thay theá khaùc vaø sau ñoù thöïc hieän haøng loaït caùc kieåm ñònh chaån
ñoaùn caùc moâ hình naøy.
Trong vieäc ñaùnh giaù xem moät moâ hình kinh teá löôïng coù ñöôïc chaáp nhaän hay khoâng thì
daáu cuûa caùc heä soá hoài quy öôùc löôïng laø moät trong nhöõng ñaïi löôïng raát quan troïng, vaø ñieàu caàn
thieát laø nhaø nghieân cöùu phaûi coù ñöôïc nhöõng nhaän ñònh ban ñaàu veà caùc giaù trò kyø voïng seõ nhaän
ñöôïc, ít nhaát laø ñoái vôùi nhöõng bieán quan troïng. Ví duï, giaû söû chuùng ta ñang öôùc löôïng cho moái
quan heä cuûa nhu caàu vaø keát quaû coù ñoä co giaõn öôùc löôïng veà giaù laø döông. Ñaây laø moät daáu hieäu
roõ raøng cho nhöõng ñaëc tröng sai coù theå coù trong thaønh phaàn xaùc ñònh hoaëc caáu truùc sai soá (hoaëc
caû hai) vaø/ hoaëc phöông phaùp luaän kinh teá löôïng coù loãi sai. Maëc duø giaù trò R 2 laø moät ñaïi löôïng
raát höõu duïng khi duøng ñeå ñaùnh giaù tính thích hôïp, nhöng tin töôûng vaøo ñaïi löôïng naøy quaù möùc
laø moät ñieàu khoâng neân. Thoâng thöôøng nhöõng cuoäc nghieân cöùu cheùo ñeàu cho keát quaû R 2 thaáp
hôn so vôùi caùc nghieân cöùu theo chuoãi thôøi gian, trong ñoù haàu heát caùc bieán ñeàu cho thaáy xu
höôùng vaø coù moái töông quan cao giöõa chuùng. Maëc duø giaù trò R 2 thaáp seõ cho thaáy khaû naêng moät
soá bieán bò loaïi boû nhöng ngöôøi ta cuõng khoâng khuyeán khích choïn löïa moät moâ hình döïa treân
tieâu chuaån cöïc ñaïi giaù trò R 2 .
Trong chöông 4, chuùng ta ñaõ ñeà caäp ñeán 8 tieâu chuaån choïn löïa moâ hình nhö laø nhöõng ñaïi
löôïng höõu ích duøng ñeå ñaùnh giaù xem moâ hình naøy coù “toát” hôn moâ hình kia hay khoâng. Moät
tieâu chuaån khaùc nöõa cuõng thöôøng ñöôïc duøng ñeå ñaùnh giaù moâ hình laø khaû naêng döï baùo giaù trò



bieán phuï thuoäc cuûa moâ hình. Neáu giaù trò döï baùo laø moät trong nhöõng muïc tieâu quan troïng ñoái
vôùi nhaø kinh teá löôïng thì khaû naêng döï baùo cuûa moâ hình caàn thieát phaûi ñöôïc xem xeùt thaän troïng
(xin xem theâm ôû chöông 11).
Trong caùc phaàn öùng duïng vaø ví duï veà tính chaát phi tuyeán vaø veà caùc bieán coù ñoä treã trình
baøy trong chöông naøy, chuùng ta ñaõ baét ñaàu vôùi moät moâ hình khoâng coù giôùi haïn toång quaùt vaø
sau ñoù giaûm ñi baèng caùch loaïi daàn töøng bieán coù heä soá yù nghóa thaáp nhaát. Caùch tieáp caän naøy,
ñöôïc goïi laø phöông phaùp ñi “töø toång quaùt ñeán ñôn giaûn”, ñöôïc taùc giaû Hendry (1985) raát taùn
thaønh cuõng nhö nhieàu nhaø kinh teá löôïng khaùc thuoäc tröôøng kinh teá London (xin tham khaûo
theâm ôû taùc giaû Hendry vaø Richards, 1982, 1983; taùc giaû Gilbert, 1986, 1989). Caùch tieáp caän
cuûa hoï coøn ñöôïc goïi laø phöông phaùp Hendry/ LSE. Maëc duø taùc giaû Hendry ñaõ nhaán maïnh
ñeán vieäc moâ hình hoaù theo chuoãi thôøi gian nhöng nguyeân lyù cuõng coù theå aùp duïng töông töï treân
döõ lieäu cheùo. YÙ töôûng cô baûn trong thuaät ngöõ cuûa taùc giaû Hendry laø coù moät quy trình phaùt ra
caùc döõ lieäu (DGP) naèm aån döôùi caùc giaù trò cuûa caùc bieán soá veà kinh teá vaø coâng vieäc cuûa nhaø
nghieân cöùu laø duøng caùc lyù thuyeát kinh teá, khaû naêng tröïc quan, vaø kinh nghieäm cuõng nhö thoâng
qua moät soá kieåm ñònh ñaùnh giaù moâ hình ñeå xem moâ hình coù theå caûi thieän ñöôïc hay khoâng. Ñeå
laøm ñöôïc ñieàu naøy, nhaø nghieân cöùu seõ baét ñaàu vôùi moät moâ hình ñoäng toång quaùt cho pheùp hoï söû
duïng nhieàu tham soá hôn, nghóa laø coù nhieàu ñoä treã vaø bieán (bao goàm caû nhöõng soá haïng phi
tuyeán coù theå coù) hôn nhöõng gì maø ngöôøi ta thöôøng tieán haønh vaø sau ñoù, nhaø nghieân cöùu seõ thöïc
hieän pheùp ñôn giaûn hoaù döïa treân döõ lieäu baèng kieåm ñònh Wald vaø kieåm ñònh t. Ví duï 6.5 vaø
öùng duïng trong phaàn 6.7 veà chi phí baèng saùng cheá vaø chi phí R&D laø nhöõng ví duï cuï theå cho
phöông phaùp luaän naøy. Trong chöông 7, 9, vaø 10, chuùng ta seõ coù nhieàu ví duï hôn veà phöông
phaùp tieáp caän töø toång quaùt ñeán ñôn giaûn. Söï ñôn giaûn hoaù moâ hình döïa treân döõ lieäu daãn tôùi keát
quaû laø moâ hình ñoù coù caùc ñaëc tröng xuùc tích hôn, coù nghóa laø moâ hình vôùi ít thoâng soá hôn. Lôïi
theá cuûa keát quaû xuùc tích naøy laø (1) taêng ñoä chính xaùc cho caùc giaù trò öôùc löôïng vì ñaõ laøm giaûm
tính ña coäng tuyeán, (2) coù nhieàu baäc töï do hôn vaø vì theá maø giaù trò öôùc löôïng seõ ñaùng tin caäy
hôn, (3) naêng löïc kieåm ñònh seõ cao hôn, vaø (4) moâ hình ñôn giaûn hôn, ngöôøi ta seõ deã daøng lónh
hoäi hôn laø moâ hình phöùc taïp.

6.14 Moâ Hình Hoaù “Töø Ñôn Giaûn Ñeán Toång Quaùt” Baèng Caùch Söû Duïng Kieåm Ñònh Nhaân Töû
Lagrange

Veà maët nguyeân taéc thì ngöôøi ta vaãn öa thích caùch tieáp caän töø toång quaùt ñeán chi tieát hôn, nhöng
nhöõng öùng duïng thöïc teá thuaàn tuùy theo phöông phaùp naøy coù theå ñem laïi moät soá phieàn toaùi. Ví
duï, vieäc ñöa theâm moät vaøi bieán môùi coù tính chaát treã so vôùi caùc bieán hieän taïi trong moâ hình seõ
khieán cho caùc bieán ñoäc laäp khaùc trôû neân töông quan vôùi nhau cao hôn. Nhö ñaõ trình baøy trong
caùc chöông tröôùc, khi möùc ñoä töông quan trôû neân cao hôn thì vieäc ño löôøng caùc aûnh höôûng
rieâng leû cuûa caùc bieán ñoäc laäp trôû neân khoù khaên hoaëc khoâng theå ñöôïc. Töông töï, thoâng thöôøng
thì nhaø nghieân cöùu seõ töï tin hôn vôùi moät moâ hình ñaëc tröng cô baûn hôn laø vieäc xaây döïng moät
moâ hình toång quaùt. Ñeå traùnh nhöõng vaán ñeà treân, vieäc moâ hình hoaù döïa treân caùch tieáp caän “töø



ñôn giaûn ñeán toång quaùt” seõ ñöôïc baét ñaàu töø phía ngöôïc laïi vôùi ñaëc tröng cô baûn veà nhöõng gì
maø nhaø nghieân cöùu caûm thaáy töï tin vaø roài caâu hoûi ñaët ra laø lieäu coù neân ñöa theâm bieán vaøo trong
moâ hình hay khoâng. Moät coâng cuï chaån ñoaùn thöôøng ñöôïc caùc nhaø nghieân cöùu söû duïng trong
caùch tieáp caän naøy laø kieåm ñònh vôùi nhaân töû Lagrange (LM). Tuy nhieân, tröôùc khi ñi saâu vaøo
vaán ñeà treân, ñieàu caàn thieát laø phaûi coù ñöôïc caùch nhìn toång quaùt ñaày ñuû veà nhöõng phöông phaùp
khaùc nhau ñoái vôùi kieåm ñònh ñaëc tröng moâ hình.
Coù nhieàu phöông phaùp chính thöùc ñöôïc duøng trong vieäc kieåm ñònh giaû thuyeát, nhöng
phöông phaùp ñöôïc duøng thöôøng xuyeân nhaát bao goàm kieåm ñònh baèng nhaân töû Lagrange (LM),
kieåm ñònh tyû soá thích hôïp (LR), vaø kieåm ñònh Wald. Trong caùc phaàn ñöôïc trình baøy tröôùc ñaây
thì kieåm ñònh ñöôïc söû duïng nhieàu nhaát laø kieåm ñònh Wald. Trong phaàn naøy, ngöôøi ta seõ taäp
trung vaøo kieåm ñònh LM nhö laø moät phöông aùn thay theá trong vieäc kieåm ñònh caùc ñaëc ñieåm
cuûa moâ hình. Kieåm ñònh LR seõ ñöôïc thaûo luaän theâm trong phaàn phuï luïc. Trong taát caû caùch tieáp
caän treân, ngöôøi ta ñaõ xaây döïng leân hai moâ hình, moâ hình giôùi haïn vaø moâ hình khoâng giôùi haïn.
Moâ hình giôùi haïn ñöôïc thieát laäp baèng caùch ñöa caùc giôùi haïn tuyeán tính hoaëc phi tuyeán tính vaøo
trong caùc thoâng soá cuûa moâ hình vaø töông öùng vôùi giaû thuyeát khoâng. Moâ hình khoâng giôùi haïn laø
moät giaûi phaùp thay theá khaùc. Trong caùc chöông tröôùc ñaây, chuùng ta ñaõ duøng phöông phaùp
Wald ñeå kieåm ñònh giaû thuyeát giöõa moâ hình khoâng giôùi haïn vaø moâ hình giôùi haïn, trong ñoù
chuùng ta coù theå boû qua moät soá bieán. Ñieàu naøy ñöôïc trình baøy nhieàu trong caùc öùng duïng theo
chuoãi thôøi gian vaø cheùo. Kieåm ñònh Wald baét ñaàu vôùi moät phöông aùn thay theá (moâ hình khoâng
giôùi haïn) vaø ñöa ra caâu hoûi laø giaû thuyeát khoâng (moâ hình giôùi haïn) coù ñöôïc öa thích hôn hay
khoâng. Kieåm ñònh tyû soá thích hôïp laø moät pheùp so saùnh tröïc tieáp giöõa hai giaû thuyeát. Nguyeân lyù
cuûa nhaân töû Lagrange baét ñaàu vôùi giaû thuyeát khoâng vaø hoûi xem coù söï dòch chuyeån veà höôùng caùc
giaûi phaùp öa thích hôn. Hay noùi caùch khaùc laø thuû tuïc LM seõ xaùc ñònh ñöôïc moät moâ hình ñôn
giaûn hôn nhöng xuùc tích hôn vaø caâu hoûi ñaët ra laø coù caàn thieát phaûi theâm bieán môùi hay khoâng.
Vì vaäy maø chuùng ta seõ baét ñaàu vôùi caùch thieát laäp cô baûn vaø tieán haønh kieåm ñònh vieäc theâm caùc
bieán môùi thay vì baét ñaàu vôùi moät moâ hình ñaày ñuû vaø kieåm ñònh xem coù neân boû bôùt ñi moät soá
caùc bieán hay khoâng. Phöông phaùp LM thì khaù toång quaùt neân coù theå aùp duïng vaøo trong nhöõng
tình huoáng khaùc seõ ñöôïc moâ taû trong caùc chöông sau. Caû hai phöông phaùp töø toång quaùt ñeán ñôn
giaûn vaø töø ñôn giaûn ñeán toång quaùt laø nhöõng phöông phaùp raát höõu duïng vaø ngöôøi ta ñeà nghò raèng
neân söû duïng caû hai phöông phaùp ñeå coù ñöôïc moät keát luaän vöõng chaéc hôn.
Coù nhieàu baøi nghieân cöùu ñeà caäp ñeán kieåm ñònh LM nhö cuûa taùc giaû Aitcheson vaø
Silvey (1958), Silvey (1959), Berndt vaø Savin (1977), Godfrey (1978), Buse (1982), vaø cuûa taùc
giaû Engle (1982, 1984). Taát caû caùc baøi nghieân cöùu treân ñoøi hoûi ngöôøi ñoïc phaûi coù kieán thöùc veà
ñaïi soá tuyeán tính. Trong chöông naøy, chuùng ta seõ ñöôïc trình baøy moät caùch toùm löôïc caùc loaïi
kieåm ñònh cuøng vôùi khaû naêng öùng duïng cuûa chuùng. Moät vaøi keát quaû lyù thuyeát khaùc cuõng seõ
ñöôïc toùm taét trong phaàn phuï luïc cuûa chöông cuøng vôùi moät baûng giaûi thích caùc thuaät ngöõ veà
nhaân töû Lagrange vaø tyû soá thích hôïp. Moät söï so saùnh ba phöông phaùp naøy döïa treân caáp soá nhaân
cuõng ñöôïc ñöa theâm vaøo trong phaàn phuï luïc vaø ñöôïc dieãn giaûi baèng ví duï ñôn giaûn. Trong
chöông, chuùng ta seõ xaùc ñònh caùc böôùc caàn thieát ñeå thöïc hieän moät kieåm ñònh LM vaø öùng duïng



chuùng vôùi döõ lieäu thöïc teá. Maëc duø kieåm ñònh LM laø kieåm ñònh treân maãu lôùn, nhöng ngöôøi ta
nhaän thaáy noù cuõng raát höõu ích ngay caû trong tröôøng hôïp soá maãu quan saùt chæ côõ 30. Kieåm ñònh
Wald cuõng coù theå aùp duïng ñoái vôùi tröôøng hôïp soá maãu quan saùt nhoû. Kieåm ñònh tyû soá thích hôïp
ñoâi khi ñöôïc aùp duïng cho côõ maãu nhoû. Nhöõng ñieåm naøy seõ ñöôïc trình baøy chi tieát hôn trong
phaàn phuï luïc.
Nhöõng giaû thuyeát vôùi nguï yù baùc boû bôùt caùc bieán laø tröôøng hôïp ñaëc bieät cuûa giaû thuyeát
loàng vaøo nhau. ÔÛ daïng loàng vaøo nhau, moâ hình giôùi haïn trôû thaønh moät moâ hình con cuûa moät
moâ hình khoâng giôùi haïn khaùc. Caùc giaû thuyeát khoâng loàng vaøo nhau laø nhöõng moâ hình hoaøn
toaøn khaùc nhau maø trong ñoù moät moâ hình khoâng theå trôû thaønh moâ hình con cuûa moät moâ hình
khaùc. Ví duï, vieäc baùc boû moät soá bieán vaø theâm moät soá bieán khaùc seõ hình thaønh neân moâ hình
khoâng loàng vaøo nhau. Trong cuoán saùch naøy, chuùng ta chæ taäp trung vaøo caùc giaû thuyeát loàng vaøo
nhau. Ñoäc giaû coù quan taâm ñeán kieåm ñònh giaû thuyeát khoâng loàng vaøo nhau coù theå tham khaûo
caùc baøi vieát cuûa taùc giaû Davidson vaø MacKinnon (1981, 1982) vaø cuûa Mackinnon (1983)
nhöng chuù yù raèng chuùng ñoøi hoûi phaûi coù kieán thöùc veà ñaïi soá tuyeán tính.

Kieåm Ñònh Nhaân Töû Lagrange Khi Theâm Caùc Bieán
Thuû tuïc kieåm ñònh LM seõ deã hieåu hôn trong tröôøng hôïp nhaø phaân tích kinh doanh hay kinh teá
muoán bieát coù neân ñöa theâm bieán vaøo trong moâ hình hay khoâng (ví duï ñöa caùc soá haïng phi
tuyeán tính vaø soá haïng töông taùc). Haõy xem xeùt moâ hình khoâng giôùi haïn vaø giôùi haïn sau ñaây:

(R) Y = β1 + β2X2 + β3X3 + … + βmXm + u
(U) Y = β1 + β2X2 + … + βmXm + βm+1Xm+1 + … + βkXk + v

Trong moâ hình U, coù (k – m) bieán môùi Xm+1, Xm+2, …, Xk (ví duï, caùc bieán phi tuyeán tính) ñaõ
ñöôïc theâm vaøo. Ñieåm thuù vò ôû giaû thuyeát khoâng naøy laø heä soá hoài quy cuûa caùc bieán theâm vaøo laø
baèng 0. Caùc böôùc thöïc hieän kieåm ñònh LM nhö sau:

Böôùc 1 H0: βm+1 = βm+2 = … = βk = 0. H1: trong soá caùc β treân toàn taïi ít nhaát moät β khaùc
khoâng.
Böôùc 2 Öôùc löôïng giaù trò R cuûa moâ hình giôùi haïn
Böôùc 3 Thu ñöôïc phaàn dö öôùc löôïng cuûa moâ hình nhö sau

ˆ ˆ ˆ ˆ
u R = Y − β1 − β 2 X 2 − β 3 X 3 − ... − β m X m
ˆ

Giaû söû caùc ñaëc tröng “ñuùng” thuoäc veà moâ hình U; trong tröôøng hôïp naøy thì neân ñöa
caùc bieán Xm+1, Xm+2, …, Xk vaøo trong moâ hình. Caùc aûnh höôûng cuûa chuùng seõ ñöôïc
quan saùt baèng phaàn dö u R . Vì vaäy, u R ñöôïc xem nhö coù lieân heä vôùi nhöõng bieán bò
ˆ ˆ
loaïi boû. Noùi caùch khaùc, neáu chuùng ta hoài quy giaù trò u R theo caùc bieán treân, chuùng ta
ˆ
seõ coù ñöôïc söï thích hôïp toát, moät chæ soá chöùng toû raèng ít nhaát coù moät soá bieán trong soá



Xm+1, Xm+2, …, Xk neân ñöôïc ñöa theâm vaøo trong moâ hình. Lyù luaän naøy daãn ñeán böôùc
tieáp theo.
Böôùc 4 Hoài quy bieán u R theo haèng soá vaø taát caû caùc bieán X, bao goàm caùc bieán trong moâ hình
ˆ
giôùi haïn. Ñieàu naøy coù nghóa laø hoài quy theo taát caû caùc bieán ñoäc laäp trong moâ hình
khoâng giôùi haïn. Chuùng ta seõ xem böôùc hoài quy thöù hai naøy laø hoài quy phuï. Taùc giaû
Engle (1982) ñaõ chöùng minh raèng, ñoái vôùi caùc maãu quan saùt lôùn, côõ maãu (n) nhaân vôùi
giaù trò R2 khoâng hieäu chænh trong hoài quy phuï naøy seõ coù phaân phoái Chi-square vôùi
baäc töï do töông ñöông vôùi soá giôùi haïn trong giaû thuyeát khoâng (ñieàu naøy ñöôïc trình
baøy trong phaàn phuï luïc 6.A.3 ñoái vôùi tröôøng hôïp hoài quy ñôn). Vì theá, trong baøi toaùn
cuûa chuùng ta, nR 2 ~ χ 2 − m . Lyù do ñöa caùc bieán ban ñaàu vaøo trong hoài quy phuï laø ñeå
k

giaù trò thoáng keâ kieåm ñònh coù ñöôïc daïng thuaän tieän. Neáu nR 2 > χ *2 m (α) thì vò trí cuûa
k−

moät ñieåm naøo ñoù treân ñoà thò phaân phoái χ k − m maø dieän tích beân phaûi ñieåm ñoù baèng
2

(α), chính laø möùc yù nghóa maø chuùng ta seõ baùc boû giaû thuyeát khoâng cho raèng taát caû heä
soá hoài quy môùi ñeàu baèng khoâng. Moät caùch khaùc, chuùng ta seõ tính giaù trò p =
P(χ 2 − m > nR2 ) vaø baùc boû giaû thuyeát khoâng neáu giaù trò p thaáp hôn möùc yù nghóa. Noùi
k

caùch khaùc, chuùng ta coù theå keát luaän raèng ít nhaát coù moät soá trong caùc bieán môùi neân
ñöôïc ñöa theâm vaøo trong moâ hình. Caùc giaù trò p cuûa moãi heä soá rieâng leû cuõng coù theå
keát luaän raèng bieán naøo neân ñöôïc ñöa vaøo.

Söû Duïng Hoài Quy Phuï Ñeå Xaùc Ñònh Caùc Bieán Ñöa Theâm Vaøo Moâ Hình Cô Baûn
Hoài quy phuï cung caáp caùc thoâng tin veà nhöõng bieán môùi ñang ñöôïc xem xeùt trôû thaønh ñoái töôïng
ñöa theâm vaøo trong moâ hình cô baûn. Thöïc teá, heä soá öôùc löôïng vaø caùc trò soá thoáng keâ lieân quan
ñeán caùc bieán môùi seõ ñöôïc ñöa theâm vaøo trong hoài quy phuï cuûa kieåm ñònh LM cuõng gioáng vôùi caùc
ñaïi löôïng coù ñöôïc töø moâ hình khoâng giôùi haïn hoaøn toaøn. Moâ hình khoâng giôùi haïn naøy seõ ñöôïc
baét ñaàu cuøng vôùi phöông phaùp töø toång quaùt ñeán ñôn giaûn. Ñieåm naøy ñaõ ñöôïc chöùng minh ñaày
ñuû bôûi taùc giaû Ramanathan (1986) vaø cuõng ñöôïc dieãn giaûi moät caùch thöïc nghieäm qua ví duï 6.7.
Maëc duø khoâng coù moät höôùng daãn lyù thuyeát roõ raøng naøo ñeå coù theå choïn ra caùc bieán töø danh saùch
hoài quy phuï, nhöng ngöôøi ta coù theå söû duïng moät quy taéc ñôn giaûn laø ñöa nhöõng bieán naøo coù heä
soá hoài quy hoaëc giaù trò p nhoû hôn 0,5. Quy taéc naøy toû ra baûo thuû hôn quy taéc chæ choïn nhöõng
bieán coù yù nghóa thöïc söï. Nhö seõ trình baøy trong ví duï 6.7 vaø 6.8, vieäc söû duïng tieâu chuaån möùc yù
nghóa moät caùch nghieâm ngaët seõ coù khuynh höôùng boû qua caùc bieán coù theå coù yù nghóa so vôùi
nhöõng bieán coù möùc yù nghóa toái thieåu bò loaïi boû. Thuû tuïc naøy töông ñöông vôùi vieäc öôùc löôïng
toaøn boä moâ hình toång quaùt roài loaïi boû taát caû caùc bieán coù giaù trò p töông öùng cao hôn 0,5.

VÍ DUÏ 6.7

Phöông phaùp kieåm ñònh LM ñöôïc dieãn giaûi tröôùc tieân vôùi döõ lieäu ñeå öôùc löôïng nhu caàu söû duïng
truyeàn hình caùp trình baøy trong phaàn DATA4-8. Döõ lieäu naøy thuoäc daïng döõ lieäu cheùo thu thaäp



töø 40 thaønh phoá (caùc bieán ñöôïc ñònh nghóa sau ñaây vaø seõ ñöôïc moâ taû chi tieát hôn trong phaàn
phuï luïc 1).

sub = soá ngöôøi ñaêng kyù treân moãi heä thoáng (tính baèng ñôn vò ngaøn)
home = soá löôïng nhaø maø heä thoáng ñi qua
inst = chi phí laép ñaët tính baèng ñoâ la
svc = chi phí dòch vuï haèng thaùng cuûa moãi heä thoáng tính baèng ñoâ la
tv = soá löôïng tín hieäu truyeàn hieäu taûi bôûi moãi heä thoáng caùp
age = tuoåi thoï cuûa moãi heä thoáng tính theo naêm
air = soá löôïng tín hieäu truyeàn hình töï do nhaän ñöôïc
y = thu nhaäp tính baèng ñoâ la treân moãi ñaàu ngöôøi

Baûng 6.4 trình baøy caùc keát quaû maùy tính rieâng phaàn coù keøm giaûi thích, cho ñoäc giaû thaáy caùc
böôùc vöøa moâ taû. Ñeå coù ñöôïc toaøn boä keát quaû, haõy thöïc haønh baøi taäp maùy tính phaàn 6.10.
Maëc duø caùc trò thoáng keâ kieåm ñònh LM cho trong ví duï ñeàu cho thaáy coù yù nghóa, nhöng
ñoâi khi pheùp kieåm ñònh cuõng coù theå cho caùc daáu traùi ngöôïc. Ñieåm naøy seõ ñöôïc trình baøy trong
ví duï tieáp theo.

Baûng 6.4 Keát Quaû Maùy Tính Rieâng Phaàn Coù Keøm Giaûi Thích Trong Ví Duï 6.7

[Tröôùc tieân, haõy öôùc löôïng moâ hình cô baûn baèng caùch hoài quy bieán sub theo bieán constant,
home, inst, svc, tv, age, air, vaø bieán y. Sau ñoù phaùt ra phaàn dö ut . Hoài quy phuï trình baøy ôû ñaây
seõ hoài quy phaàn dö ut theo caùc bieán trong moâ hình cô baûn vaø coäng taát caû caùc soá haïng bình
phöông cuûa caùc bieán, bieåu dieãn döôùi daïng sq_x (ví duï sq_home = home2).]

Dependent variable: Ut

VARIABL COEFFICIENT STDERROR T STAT 2Prob(t > T)
E
0) const -481.4363 264.2862 -1.822 0.080496 *
2) home 0.0339 0.0839 0.404 0.689961
3) inst 0.9184 2.1242 0.432 0.669195
4) svc 10.1055 19.1942 0.526 0.603188
5) tv -1.4180 2.6542 -0.534 0.597895
6) age -2.5507 1.4623 -1.744 0.093391 *
7) air 23.8229 5.2392 4.547 0.000121 ***
8) y 0.0829 0.0526 1.576 0.127509
9) sq_home 0.0002207 0.0002839 0.778 0.444146
10) sq_inst -0.0210 0.0655 -0.321 0.750748
11) sq_svc -0.7790 1.2854 -0.606 0.549977
12) sq_tv 0.0484 0.1017 0.476 0.637925



13) sq_age 0.1393 0.0734 1.898 0.069252 *
14) sq_air -1.5823 0.3732 -4.240 0.000267 ***
15) sq_y -4.547e-006 2.8346e-006 -1.604 0.121287


[Trò thoáng keâ LM = soá laàn quan saùt nhaân vôùi giaù trò chöa hieäu chænh R2 = 21,992652.]

Chi-square (7): area to right of 21.992652 = 0.002548.

[Giaû thuyeát khoâng ñoái vôùi kieåm ñònh LM laø heä soá cuûa taát caû baûy bieán bình phöông ñöôïc ñöa
theâm vaøo moâ hình seõ baèng 0] (vì vaäy, baäc töï do laø 7). Giaù trò p baèng 0,002548 cho thaáy chuùng
ta “an toaøn” khi quyeát ñònh baùc boû giaû thuyeát khoâng vaø keát luaän raèng coù ít nhaát moät vaøi trong
soá caùc bieán ñöôïc ñöa theâm vaøo thuoäc veà moâ hình. (Söû duïng maùy tính caàm tay ñeå kieåm tra trò
thoáng keâ kieåm ñònh LM vaø thöïc hieän kieåm ñònh Chi-square baèng caùch söû duïng möùc yù nghóa
1% vôùi baûng phaân phoái Chi-square).

Baûng 6.4 (Tieáp theo)
Hoài quy phuï seõ giuùp chuùng ta quyeát ñònh nhöõng bieán môùi naøo seõ ñöôïc ñöa theâm vaøo
trong moâ hình. Tuy nhieân, ngöôøi ta cuõng khoâng coù nhöõng höôùng daãn naøo veà maët lyù thuyeát ñoái
vôùi vieäc choïn löïa trong thöïc teá. Vì theá, chuùng ta seõ söû duïng quy taéc tuøy yù laø ñöa nhöõng bieán
môùi coù giaù trò p nhoû hôn 0,5 vaøo trong moâ hình, töông ñöông vôùi möùc yù nghóa 50%. Quy taéc
naøy baûo thuû hôn caû khi ta söû duïng ñieåm ngöôõng 10% maø chuùng ta söû duïng laâu nay vaø noù cuõng
ñöôïc thieát keá ñeå cöïc tieåu hoaù caùc sai leäch coù theå coù töø caùc bieán bò boû qua vôùi nguyeân nhaân
khoâng ñöa ñuû bieán vaøo trong moâ hình. Theo quy taéc “0,5”, trò bình phöông cuûa bieán home, age,
air, vaø y ñöôïc ñöa theâm vaøo trong moâ hình cô baûn. Ñieàu naøy seõ ñöôïc thöïc hieän tieáp theo ñaây.
Chuù yù raèng bieán phuï thuoäc hieän taïi laø sub. Loãi maø ngöôøi ta hay phaïm phaûi ôû ñieåm naøy laø ñieàu
chænh bieán ut nhö laø bieán phuï thuoäc hoaëc ñöa bieán naøy vaøo trong nhoùm caùc bieán ñoäc laäp. Ñieàu
naøy roõ raøng laø sai vaø khoâng coù yù nghóa.]

Dependent variable: sub

E
0) const -407.0791 211.7804 -1.922 0.064813 *
2) home 0.4319 0.0792 5.451 0.000008 ***
3) inst -0.1821 0.3957 -0.460 0.648969
4) svc 0.2123 1.9666 0.108 0.914822
5) tv 0.6962 0.5292 1.315 0.199029
6) age -1.0718 1.2305 -0.871 0.391149
7) air 18.1986 4.8824 3.727 0.000868 ***
8) y 0.0757 0.0476 1.591 0.122767
9) sq_home 0.0002240 0.0002689 0.833 0.411944



13) sq_age 0.1174 0.0580 2.025 0.052478 *
14) sq_air -1.5579 0.3383 -4.605 0.000082 ***
15) sq_y -4.049e-006 2.5562e-006 -1.584 0.124383

Mean of dep. Var. 24.509 S.D. of dep. Variable 33.537
F-statistic(11,28) 45.8496 p-value for F() 0.000000


SGMASQ 82.3995 AIC 105.099 FPE 107.119
GCV 117.714 RICE 144.199

Excluding the constant, p-value was highest for variable 4 (svc)

[Phaàn cuoái cuûa thuû tuïc laø laøm goïn moâ hình döïa treân döõ lieäu maø chuùng ta nhaän ñöôïc tröôùc ñaây.
Ñieàu naøy ñöôïc thöïc hieän baèng caùch loaïi boû lieân tieáp caùc bieán coù giaù trò p cao nhaát, nhöng phaûi
loaïi boû töøng bieán moät. Ñeå traùnh laàm laãn neáu trình baøy quaù nhieàu keát quaû khoâng caàn thieát neân
treân trang taøi lieäu naøy chæ ñöa ra moâ hình cuoái cuøng.]


E
0) const -562.6761 158.0817 -3.559 0.001185 ***
2) home 0.4960 0.0283 17.525 0.000000 ***
6) age -1.5575 0.9037 -1.723 0.094460 *
7) air 17.3047 4.3410 3.986 0.000364 ***
8) y 0.1108 0.0348 3.186 0.003215 ***
13) sq_age 0.1392 0.0438 3.181 0.003251 ***
14) sq_air -1.4177 0.2919 -4.856 0.000030 ***
15) sq_y -5.948e-006 1.8798e-006 -3.164 0.003399 ***

Mean of dep. Var. 24.509 S.D. of dep. Variable 33.537
F-statistic(11,28) 74.9412 p-value for F() 0.000000
Durbin-Watson stat. 2.069 First-order autocorr. coeff -0.051




SGMASQ 78.8104 AIC 94.0571 FPE 94.5725
GCV 98.513 RICE 105.081

[Ñeå laøm roõ söï töông phaûn giöõa phöông phaùp töø ñôn giaûn ñeán toång quaùt naøy vôùi phöông phaùp
Hendry/ LSE moâ hình hoaù töø toång quaùt ñeán ñôn giaûn, chuùng ta seõ öôùc löôïng moâ hình toång quaùt
nhaát bao quaùt ñöôïc soá haïng tuyeán tính vaø bình phöông baäc hai. Moät chuù yù thuù vò laø caùc heä soá
vaø sai soá chuaån cuûa bình phöông caùc soá haïng theâm vaøo cuõng gioáng nhö caùc soá haïng trong hoài
quy phuï trình baøy ôû treân. Muoán bieát theâm caùch chöùng minh veà maët lyù thuyeát raèng taïi sao
tröôøng hôïp naøy luoân luoân xaûy ra, haõy tham khaûo taùc giaû Ramanathan (1986).]

Dependent variable: sub

VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > T)

0) const -488.2440 264.2862 -1.847 0.076556 *
2) home 0.4394 0.0839 5.238 0.000020 ***
3) inst 0.3920 2.1242 0.185 0.855089
4) svc 12.1443 19.1942 0.633 0.532671
5) tv -0.6615 2.6542 -0.249 0.805230
6) age -1.3571 1.4623 -0.928 0.362229
7) air 18.7117 5.2392 3.572 0.001475 ***
8) y 0.0845 0.0526 1.608 0.120423
9) sq_home 0.0002207 0.0002839 0.778 0.444146
10) sq_inst -0.0210 0.0655 -0.321 0.750748
11) sq_svc -0.7790 1.2854 -0.606 0.549977
12) sq_tv 0.0484 0.1017 0.476 0.637925
13) sq_age 0.1393 0.0734 1.898 0.069252 *
14) sq_air -1.5823 0.3732 -4.240 0.000267 ***
15) sq_y -4.547e-006 2.8346e-006 -1.604 0.121287


[Theo chieán löôïc giaûn löôïc moâ hình döïa treân döõ lieäu, chuùng ta laàn löôït loaïi boû caùc bieán coù heä
soá khoâng yù nghóa. Moâ hình cuoái cuøng ñöôïc xaùc ñònh theo caùch naøy gioáng nhö moâ hình tìm
ñöôïc tröôùc ñaây theo phöông phaùp töø ñôn giaûn ñeán toång quaùt. Nhö vaäy, trong ví duï naøy, hai
phöông phaùp laø töông ñöông. Vì ñieàu naøy khoâng phaûi luùc naøy cuõng xaûy ra, ngöôøi ta ñeà nghò söû
duïng caû hai phöông phaùp vaø thöïc hieän kieåm tra cheùo. Tuy nhieân, neáu caàn phaûi choïn moät trong
hai caùch tieáp caän, caùch tieáp caän Hendry/LSE thöôøng ñöôïc söû duïng hôn vì bieän phaùp tieáp caän



naøy chaéc chaén hôn vaø khoâng phuï thuoäc vaøo quy taéc 0,5 chuû quan khi choïn caùc bieán töø vieäc hoài
quy phuï. Tuy nhieân, trong chöông 8, 9, vaø 10 chuùng ta seõ thaáy raèng kieåm ñònh LM laø moät thuû
tuïc kieåm ñònh cöïc kyø maïnh trong nhöõng tình huoáng khaùc]

Trong ví duï 6.7, chuùng ta loaïi boû caùc bieán döïa treân möùc yù nghóa cuûa caùc heä soá hoài quy cuûa
chuùng. Baét ñaàu töø moâ hình toång quaùt nhaát theo phöông phaùp Hendry/LSE vaø loaïi boû töøng bieán
moät nhö tröôùc ñaây, nhöng giöõ laïi bieán thu nhaäp (income), phí dòch vuï haøng thaùng (monthly
service charge), vaø phí laép ñaët (installation fee) cho ñeán cuoái cuøng bôûi vì chuùng laø caùc soá ño
veà thu nhaäp vaø giaù trong phöông trình ñöôøng caàu vaø vì vaäy coù yù nghóa veà maët lyù thuyeát. So
saùnh moâ hình cuoái cuøng thu ñöôïc (veà maët tieâu chí choïn löïa vaø möùc yù nghóa cuûa caùc heä soá) vôùi
moâ hình cuoái cuøng ôû baûng 6.4. Baïn thaáy nhöõng khaùc bieät gì? Baïn seõ ñeà nghò söû duïng moâ hình
naøo ñeå thöïc hieän dieãn dòch cuoái cuøng? Haõy söû duïng moâ hình ñoù ñeå dieãn dòch caùc keát quaû.

VÍ DUÏ 6.8

Ví duï minh hoïa thöù hai naøy seõ trình baøy caùch thöùc aùp duïng kieåm ñònh LM cho baøi taäp ñöôïc
nghieân cöùu ôû ví duï 6.5, nghóa laø, trong moâ hình tuyeán tính loâgarít veà tieàn löông. Baûng 6.5 trình
baøy keát quaû maùy tính coù chuù thích veà tröôøng hôïp naøy (xem chi tieát ôû Phaàn Thöïc Haønh Maùy
Tính 6.11). Giaù trò R2 khoâng hieäu chænh cuûa hoài quy phuï chæ baèng 0,079, vôùi trò thoáng keâ nR2
baèng 3,86. Theo giaû thuyeát khoâng caùc soá haïng baäc hai coù heä soá baèng 0, giaù trò naøy tuaân theo
phaân phoái Chi bình phöông vôùi 3 baäc töï do. Giaù trò p-value baèng 0,28 cho thaáy raèng chuùng ta
khoâng theå baùc boû giaû thuyeát H0 moät caùch an toaøn. Ñieàu naøy haøm yù raèng khoâng moät bieán môùi
naøo coù heä soá coù yù nghóa. Tuy nhieân, löu yù raèng giaù trò p-value cuûa heä soá cuûa bieán EDUC2 coù yù
nghóa taïi möùc 7,33%, ñaây laø möùc yù nghóa chaáp nhaän ñöôïc. Vì vaäy, hoài quy phuï ñeà nghò bieán
naøy ñöôïc ñöa vaøo moâ hình (quy taéc p-value 0,5 cuõng seõ choïn bieán naøy vaø loaïi taát caû caùc bieán
coøn laïi). Ngöôïc laïi, kieåm ñònh nR2 cho thaáy khoâng coù bieán naøo caàn ñöa vaøo moâ hình. Do ñoù,
kieåm ñònh LM ñöa ra caùc keát luaän traùi ngöôïc nhau veà möùc ñoä quan troïng cuûa vieäc theâm moät
bieán môùi vaøo moâ hình ban ñaàu.

Baûng 6.5 Baùo Caùo Coù Chuù Giaûi Moät Phaàn In Töø Maùy Tính Cho Ví Duï 6.8

[Öôùc löôïng hoài quy phuï]

VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t>|T|
0) const 0.4934 0.8092 0.610 0.545334
2) EDUC -0.1576 0.0864 -1.824 0.075224 *
3) EXPER -0.0088 0.0245 -0.361 0.719991
4) AGE -0.0008179 0.0338 -0.024 0.980822
7) sq_EDUC 0.0115 0.0063 1.837 0.073294 *



8) sq_EXPER 0.0004293 0.0011 0.384 0.703130
9) sq_AGE 0.0000211 0.0003814 0.055 0.956041

Unadjusted R-squared = 0.079
Value of the LM statistic = 3.861657
Chi-square (3): area to the right of 3.861657 = 0.276796

[Löu yù raèng p-value cho bieát khoâng theå baùc boû giaû thuyeát khoâng, nhöng heä soá cuûa bieán EDUC2
coù yù nghóa taïi möùc yù nghóa 7,33%]

Trong ví duï naøy, phöông phaùp töø toång quaùt ñeán ñôn giaûn seõ toát hôn vì seõ traùnh ñöôïc söï mô hoà.
Tuy nhieân, neáu chuùng ta söû duïng quy taéc p-value 0,5 trong vieäc choïn bieán, hai phöông phaùp laø
nhö nhau.

Ví duï treân giaûi thích raèng, maëc duø kieåm ñònh LM laø moät coâng cuï chaån ñoaùn höõu ích trong vieäc
xaây döïng moät khung phaân tích töø ñôn giaûn ñeán toång quaùt, trong moät soá tröôøng hôïp tính höõu ích
cuûa chuùng bò haïn cheá. Tuy nhieân, chuùng ta seõ thaáy ôû caùc chöông 8, 9, vaø 10 raèng kieåm ñònh
LM raát maïnh trong nhieàu tình huoáng.

6.15 Thuû Tuïc RESET Ramsey Ñeå Xaùc Ñònh Sai Soá Ñaëc Tröng Hoài Quy

Ramsey (1969) ñeà ra moät phöông phaùp khaùc ñeå kieåm ñònh ñaëc tröng cuûa moâ hình. Noù ñöôïc
goïi laø RESET (kieåm ñònh sai soá ñaëc tröng hoài quy). Vieäc aùp duïng thuû tuïc naøy cuõng deã daøng
nhö vieäc aùp duïng kieåm ñònh LM ñöôïc moâ taû ôû phaàn tröôùc. Caùc böôùc cuûa thuû tuïc RESET ñöôïc
thöïc hieän nhö sau:
ˆ
Böôùc 1: Öôùc löôïng moâ hình theo thuû tuïc OLS vaø löu caùc giaù trò ñöôïc thích hôïp Yt .
ˆ ˆ ˆ
Böôùc 2: Theâm caùc bieán Yt2 , Yt3 , vaø Yt4 vaøo moâ hình ôû böôùc 1 vaø öôùc löôïng moâ hình môùi
Böôùc 3: Thöïc hieän kieåm ñònh F Wald cho vieäc loaïi boû ba bieán môùi trong böôùc 2. Neáu giaû
thuyeát khoâng cho raèng caùc bieán môùi khoâng coù hieäu öùng bò baùc boû, ñoù chính laø daáu
hieäu cuûa sai soá ñaëc tröng.

Cô sôû cuûa thuû tuïc RESET Ramsey laø caùc phaàn dö öôùc löôïng ( u t ) maø ñaïi dieän cho caùc taùc ñoäng
ˆ
bieán bò loaïi boû coù theå ñöôïc tính xaáp xæ baèng toå hôïp tuyeán tính cuûa caùc luõy thöøa cuûa caùc giaù trò
ñöôïc thích hôïp. Neáu caùc luõy thöøa naøy coù caùc taùc ñoäng coù yù nghóa, thì moâ hình goác ñöôïc coi
nhö ñaõ bò ñaëc tröng sai. Tuy nhieân, nhöôïc ñieåm chính cuûa phöông phaùp RESET laø kieåm ñònh
seõ khoâng chæ ra ñöôïc loaïi ñaëc tröng sai vaø cuõng khoâng gôïi yù daïng haøm thích hôïp caàn söû duïng.
Tuy vaäy, kieåm ñònh naøy boå sung cho caùc kieåm ñònh Wald vaø LM ñöôïc öùng duïng ñeå kieåm ñònh
caùc taùc ñoäng ñoäng vaø phi tuyeán ñaëc thuø. Ñieåm naøy ñöôïc minh hoïa trong ví duï döôùi ñaây.



VÍ DUÏ 6.9

Trong ví duï 6.2, chuùng ta ñaõ söû duïng taäp döõ lieäu DATA6-1 ñeå öôùc löôïng haøm chi phí trung
bình cuûa moät coâng ty saûn xuaát. Ñaàu tieân chuùng ta söû duïng thuû tuïc RESET ñeå kieåm ñònh xem
quan heä tuyeán tính ñaõ ñuû theå hieän baûn chaát baøi toaùn chöa (xem Phaàn Thöïc Haønh Maùy Tính
6.12 veà caùc böôùc ñeå chaïy laïi caùc keát quaû cuûa ví duï naøy). Nhö vaäy, chuùng ta hoài quy bieán
UNITCOST theo soá haïng haèng soá, OUTPUT, vaø INPCOST, vaø löu caùc trò öôùc löôïng cuûa Y
ˆ
( Y ). Tieáp theo chuùng ta tieán haønh hoài quy bieán UNITCOST theo caùc bieán treân vaø theâm caùc
luõy thöøa cuûa trò öôùc löôïng Y vaø thöïc hieän kieåm ñònh F Wald cho caùc luõy thöøa cuûa Y . Trò ˆ
thoáng keâ tính toaùn F baèng 3,7447, trò naøy, theo giaû thuyeát khoâng laø caùc bieán ñöôïc theâm vaøo
khoâng taùc ñoäng ñeán UNITCOST, coù phaân phoái F vôùi 3 baäc töï do ôû töû soá vaø 14 (=20 – 6) baäc töï
do ôû maãu soá. Giaù trò p-value töông öùng laø 0,036407, coù nghóa raèng caùc heä soá cuûa caùc bieán
ñöôïc theâm vaøo coù yù nghóa keát hôïp döôùi möùc 5%. Noùi caùch khaùc, thuû tuïc RESET chæ ra söï ñaëc
tröng sai moâ hình. Trong ví duï 6.2, chuùng ta theâm vaøo soá haïng baäc hai ñoái vôùi bieán OUTPUT
vaø nhaän thaáy bieán ñoù coù moät taùc ñoäng coù yù nghóa (ñieàu naøy cuõng chaúng coù gì ngaïc nhieân bôûi vì
lyù thuyeát cho chuùng ta thaáy ñöôøng cong chi phí trung bình coù daïng toång quaùt hình chöõ U).
Ñieàu naøy ñoøi hoûi tröôùc tieân phaûi hoài quy bieán UNITCOST theo moät soá haïng haèng soá,
OUTPUT, INPCOST, vaø OUTPUT2 vaø löu caùc trò öôùc löôïng Y nhö tröôùc ñoù. Sau ñoù theâm luõy
thöøa cuûa trò Y öôùc löôïng vaøo laøm bieán giaûi thích vaø söû duïng kieåm ñònh F Wald ñoái vôùi caùc bieán
ñöôïc theâm vaøo naøy. Trò thoáng keâ F laø 0,4826 vôùi trò p-value baèng 0,7. Vì giaù trò naøy quaù cao,
chuùng ta khoâng theå baùc boû giaû thuyeát khoâng raèng caùc bieán ñöôïc theâm vaøo khoâng coù aûnh höôûng
ñeán bieán UNITCOST. Nhö vaäy, phöông phaùp RESET cho raèng moâ hình cuoái cuøng trong Ví duï
6.2 coù theå khoâng bò ñaëc tröng sai.

Aùp duïng thuû tuïc RESET ñeå kieåm ñònh ñaëc tröng sai trong moâ hình cuoái cuøng ôû phaàn baøi taäp ví
duï 6.7.

Laøm töông tö cho moâ hình cuoái cuøng trong Ví duï 6.5

Toùm Taét

Moâ hình hoài quy tuyeán tính ñôn cuõng coù theå ñöôïc söû duïng ñeå giaûi quyeát caùc quan heä khoâng
tuyeán tính, vôùi ñieàu kieän laø moâ hình tuyeán tính trong caùc thoâng soá. Caùc daïng haøm khaùc nhau
thöôøng ñöôïc söû duïng laø moâ hình baùn loâgarít hoaëc tuyeán tính-loâgarít, quan heä loâgarít-tuyeán
tính, moâ hình loâgarít hai laàn, vaø pheùp bieán ñoåi nghòch ñaûo.



Bình phöông vaø luõy thöøa cao hôn cuûa caùc bieán ñoäc laäp, hoaëc ñoä treã cuûa caùc bieán, deã daøng
ñöôïc xem xeùt trong moâ hình mieãn laø caùc heä soá hoài quy chöa bieát döôøng nhö coù daïng tuyeán tính.
Chæ caàn bieán ñoåi döõ lieäu thích hôïp vaø ñöa chuùng vaøo trong moâ hình. Taùc ñoäng caän bieân cuûa
moät bieán coù theå ñöôïc taïo ra ñeå phuï thuoäc vaøo moät bieán giaûi thích khaùc thoâng qua caùc soá haïng
töông taùc. Moät soá moâ hình khoâng theå bieán ñoåi ñöôïc veà daïng coù caùc thoâng soá tuyeán tính. Trong
nhöõng tröôøng hôïp nhö vaäy, thuû tuïc öôùc löôïng bao goàm phöông phaùp bình phöông nhoû nhaát phi
tuyeán hoaëc phöông phaùp thích hôïp cöïc ñaïi.
Vieäc so saùnh giaù trò R2 cuûa caùc moâ hình seõ khoâng ñuùng tröø phi chuùng coù cuøng caùc bieán
phía beân tay traùi cuûa moâ hình. Neáu caùc bieán phuï thuoäc khaùc nhau, chuùng ta coù theå söû duïng caùc
moâ hình khaùc ñeå döï ñoaùn giaù trò cuûa cuøng bieán ñoù vaø keá ñoù tính heä soá töông quan cuûa caùc giaù
trò tieân ñoaùn vaø quan saùt cuûa bieán naøy. Caùc heä soá töông quan naøy coù theå ñöôïc so saùnh vôùi nhau
giöõa caùc moâ hình. Tuy nhieân caàn löu yù raèng caùc döï baùo veà möùc ñoä cuûa bieán ñoäc laäp ñöôïc taïo
ra töø caùc moâ hình tuyeán tính-loâgarít vaø loâgarít hai laàn laø thieân leäch vaø khoâng nhaát quaùn vaø caàn
coù heä soá hieäu chænh.
Ba phöông phaùp thöôøng ñöôïc söû duïng nhaát trong kieåm ñònh giaû thuyeát loàng vaøo nhau -
nghóa laø, trong caùc giaû thuyeát maø trong ñoù moâ hình giôùi haïn laø taäp con cuûa moät moâ hình khoâng
giôùi haïn toång quaùt hôn. Ñoù laø caùc kieåm ñònh Wald, kieåm ñònh tæ soá thích hôïp (LR), vaø kieåm ñònh
nhaân töû Lagrange (LM). Phöông phaùp Wald (coøn ñöôïc goïi laø phöông phaùp laäp moâ hình töø
“toång quaù ñeán ñôn giaûn” Hendry/LSE) laäp moâ hình vôùi nhieàu bieán ñoäc laäp vaø caùc ñoä treã cuûa
chuùng vaø keá ñeán seõ hoûi lieäu raèng coù loaïi bôùt moät soá bieán khoâng. Kieåm ñònh LM lieân quan ñeán
vieäc laäp moâ hình cô baûn vaø tieáp theo laø lieäu coù neân theâm bieán naøo khaùc naøo moâ hình khoâng.
Ñaây laø phöông phaùp “töø ñôn giaûn ñeán toång quaùt”. Caû hai phöông phaùp söû duïng söï phaùn ñoaùn
vaø ñeàu höõu duïng, tuøy vaøo tình huoáng. Kieåm ñònh LR xem hai moâ hình töông ñöông.
Maëc duø moät caùch tieäm caùch (nghóa laø, vôùi côõ maãu lôùn) ba kieåm ñònh naøy töông ñöông,
kieåm ñònh LM höõu duïng trong caùc tình huoáng toång quaùt hôn. Noù cuõng höõu duïng trong vieäc
kieåm ñònh caùc taùc ñoäng phi tuyeán vaø söï toàn taïi cuûa caùc soá haïng töông taùc. Kieåm ñònh LM ñöôïc
tieán haønh theo ba böôùc: (1) hoài quy bieán phuï thuoäc theo moät nhoùm bieán ñoäc laäp cô baûn, bao
goàm caû soá haïng haèng soá; (2) xaùc ñònh caùc phaàn dö töø thuû tuïc OLS ñöôïc thöïc hieän ôû Böôùc (1);
vaø (3) hoài quy caùc phaàn dö theo taát caû caùc giaù trò cuûa X trong Böôùc (1), cuõng nhö caùc bieán môùi
(m veà soá löôïng), maø coù theå goàm caùc soá haïng phi tuyeán hoaëc tích cheùo (bình phöông vaø töông
taùc) cuûa caùc bieán ñoäc laäp.

Neáu tích cuûa côõ maãu (n) vaø R2 khoâng hieäu chænh töø pheùp hoài quy phuï naøy (nghóa laø, nR2) lôùn
hôn χ2m(α), ñieåm naèm treân phaân phoái Chi bình phöông vôùi m baäc töï do, veà phía phaûi sao cho
phaàn dieän tích laø α (möùc yù nghóa), thì giaû thuyeát khoâng cho raèng taát caû m bieán ñöôïc theâm vaøo
coù heä soá baèng 0 bò baùc boû. Neáu giaû thuyeát bò baùc boû, trò t-values trong Böôùc (3) seõ giuùp xaùc
ñònh caùc bieán coù theå ñöôïc theâm vaøo moâ hình cô baûn. Ngay caû neáu kieåm ñònh nR2 khoâng baùc
boû ñöôïc giaû thuyeát khoâng veà caùc heä soá baèng 0, trò thoáng keâ t cuûa pheùp hoài quy phuï coù theå gôïi yù
raèng moät soá bieán neân ñöôïc theâm vaøo. Sau ñoù caùc bieán naøy coù theå ñöôïc theâm vaøo moâ hình cô



baûn ñeå thöïc hieän caùc taäp öôùc löôïng môùi. Trong caùc chöông sau chuùng ta seõ thaáy raèng caùc
nguyeân taéc cuûa thuû tuïc kieåm ñònh LM coù theå aùp duïng ñöôïc trong caùc tröôøng hôïp toång quaùt hôn.
Kieåm ñònh sai soá ñaëc tröng hoài quy Ramsey (RESET) cuõng coù theå ñöôïc söû duïng ñeå kieåm
ˆ
ñònh ñaëc tröng cuûa moâ hình. Ñaàu tieân moâ hình ñöôïc öôùc löôïng vaø caùc trò öôùc löôïng cuûa Y ( Y )
ˆ ˆ ˆ
ñöôïc löu laïi. Caùc bieán Yt2 , Yt3 , vaø Yt4 ñöôïc theâm vaøo moâ hình vaø kieåm ñònh F keát hôïp ñöôïc
thöïc hieän cho caùc heä soá. Neáu caùc heä soá laø coù yù nghóa keát hôïp, ñaây seõ laø daáu hieäu cuûa ñaëc tröng
sai moâ hình. Tuy nhieân, thuû tuïc naøy khoâng xaùc ñònh baûn chaát cuûa ñaëc tröng sai. Duø vaäy,
phöông phaùp RESET coù theå laø moät phöông phaùp boå sung höõu ích cho kieåm ñònh Wald, LM vaø
LR veà ñaëc tröng moâ hình.

Thuaät ngöõ

Auxilary Regression Hoài quy phuï
Base Cô sôû
Box – Cox transformation Pheùp bieán ñoåi Box – Cox
Cobb – Douglas production function Haøm saûn xuaát Cobb – Douglas
Constant returns to scale Lôïi nhuaän khoâng ñoåi theo quy moâ
Data – based simplication Ñôn giaûn hoùa döïa treân döõ lieäu
Data generation process Quaù trình phaùt döõ lieäu
Decreasing returns to scale Lôïi nhuaän giaûm daàn theo quy moâ
Derivative Ñaïo haøm
Double-log model Moâ hình loâgarít hai laàn
Dynamic model Moâ hình ñoäng
Elasticity Ñoä co giaõn
Elasticity of output with respect to capital Ñoä co giaõn cuûa saûn löôïng theo voán
Elasticity of output with respect to labor Ñoä co giaõn cuûa saûn löôïng theo lao ñoäng
Exponent Soá muõ e
Exponential function Haøm soá muõ
General to simple approach Phöông phaùp töø toång quaùt ñeán ñôn giaûn
Hendry/LSE approach Phöông phaùp Hendry/LSE
Increasing returns to scale Lôïi nhuaän taêng daàn theo quy moâ
Instantaneous rate of growth Tæ leä taêng tröôûng töùc thôøi
Interaction terms Soá haïng töông taùc
Lagrange multiplier (LM) test Kieåm ñònh nhaân töû Lagrange (LM)
Lags in behavior Ñoä treã veà haønh vi
Likelihood ratio (LR) test Kieåm ñònh tæ soá thích hôïp
Linear-log model Moâ hình loâgarít-tuyeán tính
Logarithmic function Haøm loâgarít
Logistic curve Ñöôøng cong Logistic



Logit model Moâ hình Logit
Log-linear model Moâ hình tuyeán tính-loâgarít
LSE approach Phöông phaùp LSE
Marginal effect Taùc ñoäng caän bieân
Natural logarithm Loâgarít cô soá e
Nested hypothesis Giaû thuyeát loàng vaøo nhau
Nonlinearity in parameters Tính phi tuyeán cuûa caùc thoâng soá
Nonested hypothesis Giaû thuyeát khoâng loàng vaøo nhau
Overparametrized Quaù nhieàu thoâng soá
Parsimonious specification Ñaëc tröng xuùc tích
Polynomial curve-fitting Thích hôïp baèng ñöôøng cong ña thöùc
Reciprocal transformation Pheùp bieán ñoåi nghòch ñaûo
Regression specification error test (RESET) Kieåm ñònh sai soá ñaëc tröng hoài quy
Semilog model Moâ hình baùn loâgarít
Simple to general approach Phöông phaùp töø ñôn giaûn ñeán toång quaùt
Spurious nonlinearity Phi tuyeán giaû taïo
Static model Moâ hình tónh
Trend-fitting Thích hôïp ñöôøng xu höôùng
Unitary elastic Co giaõn ñôn vò

6.A PHUÏ LUÏC

CHI TIEÁT VEÀ CAÙC KIEÅM ÑÒNH LR, WALD VAØ LM

Phuï luïc naøy cung caáp caùc chi tieát lyù thuyeát veà kieåm ñònh Wald, tæ soá thích hôïp vaø nhaân töû
Lagrange. Tuy nhieân, tröôùc khi xem phaàn naøy baïn neân ñoïc phaàn 2.A.3 veà nguyeân taéc thích
hôïp cöïc ñaïi vaø phaàn 3.A.5 veà öùng duïng cuûa noù ñoái vôùi moâ hình hoài quy tuyeán tính ñôn. Maëc duø
ba kieåm ñònh naøy coù theå öùng duïng trong nhieàu tröôøng hôïp nhöng ôû ñaây chuùng ta vaãn neân taäp
trung vaøo caùc vaán ñeà hoài quy, ñaëc bieät laø moâ hình sau ñaây:

yt = βxt + ut (6.A.1)

Nhöõng chöõ vieát thöôøng theå hieän caùc ñoä leäch cuûa caùc bieán so vôùi giaù trò trung bình töông
öùng. Nhö ñaõ trình baøy ôû phaàn 4.A.1, lôïi ích cuûa caùch tieáp caän naøy laø loaïi boû haèng soá. Theo söï
giaû ñònh naøy, caùc giaù trò u tuaân theo phaân phoái chuaån coù trung bình laø 0, phöông sai σ2, logarit
cuûa haøm thích hôïp ñoái vôùi taäp hôïp caùc quan saùt y1, y2, …, yn vaø tham soá β chöa bieát ñöôïc vieát
nhö sau (quaù trình naøy töông töï nhö quaù trình trong phaàn 3.A.5).



∑ (y − βxt )
2

ln L = − nlnσ − nln ( 2π ) − (6.A.2)
t

2σ 2

Giaû thuyeát khoâng maø chuùng ta ñang xem xeùt coù daïng β = β0 vaø giaû thuyeát ngöôïc laïi β ≠ β0.
Khi β0 = 0, ñieàu naøy töông ñöông vôùi caâu hoûi lieäu bieán soá x coù thuoäc veà moâ hình khoâng. Moãi
thuû tuïc kieåm ñònh ñöôïc thaûo luaän rieâng reõ, vaø sau ñoù thöïc hieän so saùnh caùc phöông phaùp veà
maët hình hoïc. Xem laïi chöùng minh cuûa Buse (1982) vaø Engle (1982) cuõng nhö Ramanathan
(1993) ñeå bieát chi tieát hôn veà ba kieåm ñònh naøy.

6.A.1 Kieåm ñònh Tæ soá Thích Hôïp

Trong thoáng keâ, thuû tuïc kieåm ñònh coå ñieån döïa treân tæ soá thích hôïp, maø theo nhöõng cuïm töø ñôn
giaûn, noù ñöôïc ñònh nghóa nhö tæ soá cuûa giaù trò lôùn nhaát cuûa haøm thích hôïp vôùi giaû thuyeát khoâng
ˆ
bò chia bôûi giaù trò lôùn nhaát cuûa noù khi khoâng bò giôùi haïn. Ñaëc bieät hôn, cho β laø öôùc löôïng thích
hôïp cöïc ñaïi cuûa tham soá. Haøm thích hôïp ñöôïc ñaùnh giaù töø nhöõng giaù trò naøy ñöôïc dieãn ñaït bôûi
L( β ), boû qua σ2. Haõy ñaët haøm thích hôïp theo giaû thuyeát β = β0 laø L(β0). Tæ soá thích hôïp ñöôïc
ˆ
xaùc ñònh nhö sau:

L( β 0 )
λ=
ˆ
L ( β)

Bôûi vì maãu soá döïa treân moâ hình khoâng giôùi haïn, neân giaù trò cuûa noù khoâng theå nhoû hôn giaù
trò cuûa töû soá. Vì theá, 0 ≤ λ ≤ 1. Neáu giaû thuyeát naøy ñuùng, baèng tröïc giaùc chuùng ta kyø voïng λ gaàn
baèng 1. Neáu λ caùch xa 1 thì LR theo giaû thuyeát khoâng khaùc vôùi LR theo moâ hình khoâng giôùi
haïn, ñoù laø giaû thuyeát ngöôïc laïi. Ñieàu naøy cho thaáy raèng chuùng ta neân baùc boû giaû thuyeát khoâng
neáu λ quaù nhoû. Kieåm ñònh LR ñöôïc thaønh laäp nhö laø moät kieåm ñònh baùc boû giaû thuyeát khoâng
neáu λ ≤ K, vôùi K ñöôïc xaùc ñònh bôûi ñieàu kieän, theo giaû thuyeát khoâng, 0 ≤ λ ≤ K töông ñöông vôùi
möùc yù nghóa (α); nghóa laø, P(0 ≤ λ ≤ K|β = β0) = α.
Trong moät soá tröôøng hôïp, vuøng tôùi haïn λ ≤ K coù theå chuyeån sang moät hình thöùc khaùc lieân
quan ñeán thoáng keâ maãu phoå bieán nhö laø thoáng keâ t hay F. Trong nhöõng tình huoáng naøy, kieåm
ñònh LR giaûm xuoáng thaønh kieåm ñònh t-, F-, hay χ2. Ví duï cho nhöõng tröôøng hôïp naøy, ngöôøi
ñoïc tham khaûo Mood, Graybill vaø Boes (1974) vaø caû Ramanathan (1993), Chöông 9. Nhöõng
kieåm ñònh khaùc trình baøy ôû Chöông 2 coù theå xuaát phaùt töø nguyeân taéc tæ soá thích hôïp. Khi λ
khoâng theå chuyeån sang daïng thoáng keâ khaùc coù phaân boá phoå bieán, thì pheùp thöû tieán haønh treân
moät löôïng maãu lôùn thöôøng ñöôïc söû duïng. Ñieàu ñoù coù theå chæ ra raèng (xem Ramanthan. 1993,
trang 228), ñoái vôùi kích côõ maãu lôùn, thoáng keâ

ˆ
LR = - 2 ln λ = 2 ln L ( β ) - 2 ln L( β 0 ) (6.A.3)



coù phaân boá chi-square vôùi baäc töï do töông ñöông vôùi soá giôùi haïn, baäc töï do baèng 1 nhö trong
ví duï cuûa chuùng ta. YÙ töôûng ñaèng sau kieåm ñònh naøy coù theå ñöôïc trình baøy moät caùch hình hoïc.
ÔÛ hình 6.A.1, logarit cuûa haøm thích hôïp ñöôïc veõ khi chæ coù duy nhaát moät tham soá trong moâ
hình. Hình veõ naèm beân döôùi truïc bôûi vì log cuûa haøm thích hôïp (noù laø moät maät ñoä phaân boá nhoû
hôn 1) laø soá aâm. Ñieåm β töông öùng vôùi tröôøng hôïp khi haøm thích hôïp ñaït giaù trò cöïc ñaïi vaø β0
ˆ
töông öùng vôùi giaû thuyeát khoâng. Kieåm ñònh LR döïa treân hieäu soá veà tung ñoä, chính laø baèng moät
nöûa LR. Neáu khoaûng caùch theo tung ñoä lôùn, giaû thuyeát khoâng bò baùc boû.

Hình 6.A.1 Bieåu dieãn hình hoïc cuûa caùc kieåm ñònh Wald, LR, vaø LM

ln L( β )
β0 ˆ
β β

ˆ
ln L( β )
1
LR
2
ln L( β 0 )

VÍ DUÏ 6.A.1

Nguyeân taéc kieåm ñònh tæ leä thích hôïp ñöôïc minh hoïa cho kieåm ñònh giaû thuyeát β = 0 trong
phöông trình (6.A.1). Baèng caùch tieán haønh nhö trong Phaàn 3.A.5 vaø söû duïng chuù thích trong
Phaàn 3.2, chuùng ta löu yù raèng haøm thích hôïp khoâng giôùi haïn chæ ñaït cöïc ñaïi khi β = Sxy/Sxx vaø
ˆ
σ 2 =∑ u t2 /n = ESS/n, trong ñoù ESS laø toång bình phöông sai soá. Giaù trò cöïc ñaïi töông öùng laø
ˆ ˆ

n n

L=
 ˆ 
 ˆt ˆ[
ˆ  1  exp − ∑ u 2 /(2σ 2 ) =  1  e -n/2

 ˆ 
 ]
 σ 2π   σ 2π 

Theo giaû thuyeát khoâng β = 0, moâ hình trôû thaønh yt = ut vaø haøm thích hôïp trôû thaønh
n n
 1   1 
2
L (σ ) = 
  [
 exp − ∑ ut2 /(2σ 2 ) = 
  ]
 exp − ∑ y t2 /(2σ 2 ) [ ]
 σ 2π   σ 2π 



~
Haøm naøy cöïc ñaïi khi σ 2 =∑ y t2 /n = TSS/n, trong ñoù TSS laø toång bình phöông. Do vaäy, giaù trò
cöïc ñaïi theo giaû thuyeát khoâng ñöôïc cho bôûi

n
~  1  -n/2
L= ~
  e

 σ 2π 

~ ˆ
ˆ ~ ˆ ~
Tæ soá thích hôïp laø λ = L /L = (σ/σ ) n = (σ 2 /σ 2 ) n/2 . Trò thoáng keâ kieåm ñònh LR laø

ˆ ~
LR = - 2 ln λ = - n ln (σ 2 /σ 2 ) = - n ln (ESS/TSS) = - n ln(1 - R 2 )

trong ñoù R2 laø R2 chöa hieäu chænh cuûa moâ hình khoâng giôùi haïn.
Ñoái vôùi nhöõng maãu lôùn, LR coù phaân phoái chi-square vôùi baäc töï do laø 1. Chuùng ta seõ baùc boû
giaû thuyeát khoâng vôùi β = 0 neáu LR > K, trong ñoù K laø ñieåm treân χ t2 maø vuøng beân phaûi cuûa K laø
möùc yù nghóa.

6.A.2 KIEÅM ÑÒNH WALD

Khoâng gioáng nhö kieåm ñònh LR, söû duïng hieäu soá tung ñoä (xem hình 6.A.1), kieåm ñònh Wald söû
duïng pheùp ño bình phöông hieäu soá hoaønh ñoä. Ñaëc bieät, hieäu soá hoaønh ñoä bình phöông (β –
β0)2, ñöôïc gaùn troïng soá bôûi haøm daïng I( β ), ñöôïc söû duïng:
ˆ
W = ( β - β0 )2 I ( β ) (6.A.4)

trong ñoù
 ∂ 2 ln L 
I ( β) = - E   (6.A.5)
 ∂β 
2

laø giaù trò kyø voïng cuûa ñaïo haøm baäc hai cuûa haøm thích hôïp-logarit theo β. Ñoù laø moät pheùp ño ñoä
cong cuûa haøm thích hôïp-logarit. Haøm I ñöôïc bieát nhö laø ma traän thoâng tin. Thuû tuïc tính toaùn
ñoái vôùi kieåm ñònh naøy coù theå ñöôïc tieán haønh baèng caùch öôùc löôïng moâ hình giôùi haïn vaø moâ hình
khoâng giôùi haïn, nhö ñaõ ñöôïc thöïc hieän trong Chöông 4, vaø baèng caùch xaây döïng moät trò thoáng
keâ F. Vieäc chöùng minh coù baøi baûn cho kieåm ñònh naøy ñoøi hoûi veà ñaïi soá tuyeán tính. (xem
Ramanathan, 1993, trang 273-275).

VÍ DUÏ 6.A.2



Trong tröôøng hôïp hoài quy ñôn, löu yù raèng β tuaân theo phaân boá N(β0, σ2/Sxx). Vì theá,
ˆ
ˆ
z = ( β - β 0 )/(σ/ S xx ) tuaân theo phaân phoái chuaån, vaø vì theá z2 laø chi-square vôùi baäc töï do baèng
1. Vì vaäy, thoáng keâ kieåm ñònh Wald töông öùng vôùi giaû thuyeát khoâng β = 0 ñöôïc cho bôûi
ˆ
W = β 2 S xx /σ 2 . Töø phöông trình (3.12) chuùng ta coù β Sxx=Sxy. Chuùng ta cuõng ñaõ tìm ra
ˆ ˆ
β Sxy=RSS, toång bình phöông hoài quy, trong Phaàn 3.A.1. Söû duïng hai keá quaû naøy, chuùng ta coù
ˆ

ˆ ˆ
β ( βS xx ) nRSS nR 2
W = = =
ESS/n ESS 1 − R 2

Nhö trong tröôøng hôïp kieåm ñònh LR, haøm naøy coù phaân phoái chi-square ñoái vôùi maãu lôùn. Giaû
thuyeát khoâng seõ bò baùc boû neáu W vöôït quaù giaù trò tôùi haïn K ñöôïc ruùt ra trong Ví duï 6.A.1.

6.A.3 KIEÅM ÑÒNH NHAÂN TÖÛ LAGRANGE

Kieåm ñònh LM trong Chöông 2 döïa treân kyõ thuaät nhaân töû Lagrange ñeå toái öu hoùa caùc raøng
buoäc. Moâ hình giôùi haïn coù ñöôïc baèng caùch aùp ñaët ñieàu kieän β baèng vôùi β0. Ñieàu naøy gôïi yù raèng
chuùng ta toái ña hoùa logarit cuûa haøm thích hôïp theo β vaøσ2, vôùi raøng buoäc β = β0. Nhö chuùng ta
ñaõ thaáy ôû Phaàn 2.A.2, ñieàu naøy töông ñöông vôùi cöïc ñaïi hoùa ln L(β) – µ(β – β0), trong ñoù µ laø
nhaân töû Lagrange. Ñieàu kieän ñaïo haøm baäc nhaát cho vieäc cöïc ñaïi hoùa laø
∂ ln L
=µ
∂β
Neáu giaû thuyeát khoâng β = β0 laø ñuùng, öôùc löôïng thích hôïp cöïc ñaïi giôùi haïn seõ gaàn vôùi giaù trò
öôùc löôïng khoâng giôùi haïn. Chuùng ta cuõng löu yù raèng neáu nhaân töû Lagrange, µ, laø 0, thì phöông
trình seõ cho giaù trò öôùc löôïng thích hôïp cöïc ñaïi. Do ñoù, nhaân töû Lagrange coù theå ñöôïc dieãn giaûi
nhö laø “giaù môø” cuûa raøng buoäc β = β0. Neáu giaù cao, raøng buoäc neân bò baùc boû vì khoâng nhaát
quaùn vôùi soá lieäu. Ñieàu naøy chính laø ñoäng cô daãn ñeán kieåm ñònh LM. Kieåm ñònh LM döïa treân
ñaïo haøm rieâng phaàn (β ln L)/∂β, ñöôïc bieát ñeán nhö haøm giaù trò ñieåm vaø ñöôïc moâ taû bôûi S.
Engle (1982), coù ñöôïc töø thoáng keâ kieåm ñònh cho moâ hình hoài quy boäi vaø cho thaáy raèng kieåm
ñònh coù theå ñöôïc thöïc hieän baèng caùch chaïy hoài quy phuï treân caùc phaàn dö öôùc löôïng cuûa moâ
hình giôùi haïn (cuõng coù theå xem Ramanthan, 1993, trang 276-277). Caùc böôùc thöïc hieän ñöôïc
trình baøy trong Phaàn 6.14. Thoáng keâ kieåm ñònh LM coù daïng

LM = S2 (β0) I(β0)-1 (6.A.6)

Trong hình 6.A.1, haøm giaù trò ñieåm, ñaïo haøm rieâng phaàn cuûa haøm thích hôïp-logarit, chính
laø ñoä doác cuûa cuûa ñoà thò taïi β0. Giaû thuyeát ngöôïc laïi töông öùng vôùi S(β) = 0: coù nghóa laø ñoä doác



gaàn tôùi 0. Vì theá, kieåm ñònh Wald döïa treân hieäu soá hoaønh ñoä giöõa β vaø β0 trong ñoà thò, kieåm
ˆ
ñònh LR döïa treân hieäu soá tung ñoä, vaø kieåm ñònh LM döïa treân ñoä doác cuûa ñöôøng cong β0. Moãi
kieåm ñònh laø pheùp ño hôïp lyù veà khoaûng caùch giöõa giaû thuyeát khoâng vaø giaû thuyeát ngöôïc laïi.
Moät caùch ñoäc laäp nhau, Engle (1982) vaø Buse (1982) ñaõ chæ ra raèng khi haøm thích hôïp-logarit
laø haøm baäc hai (nhö phöông trình ôû Phaàn 6.A.2), thì taát caû ba thuû tuïc kieåm ñònh naøy ñeàu cho
keát quaû nhö nhau. Ñoái vôùi moät moâ hình tuyeán tính toång quaùt, coù söï baát caân xöùng veà raøng buoäc
giöõa ba tieâu chuaån kieåm ñònh. Ñieàu naøy ñöôïc theå hieän nhö sau:

W ≥ LR ≥ LM

Ñieàu ñoù coù nghóa laø baát cöù khi naøo kieåm ñònh LM baùc boû giaû thuyeát khoâng vôùi caùc heä soá
zero, thì caùc kieåm ñònh khaùc cuõng vaäy. Töông töï, baát cöù khi naøo kieåm ñònh Wald khoâng baùc boû
giaû thuyeát khoâng thì caùc kieåm ñònh khaùc cuõng vaäy. Noùi moät caùch maùy moùc, kieåm ñònh LR thì
röôøm raø nhaát, tröø khi chuyeån ñoåi sang kieåm ñònh t, F, hay kieåm ñònh χ2. Hai caùch kieåm ñònh
khaùc ñôn giaûn hôn, nhö ñaõ theå hieän trong taøi lieäu.

VÍ DUÏ 6.A.3
Trong tröôøng hôïp hoài qui ñôn, haøm giaù trò ñieåm ñöôïc cho bôûi

∂ ln L ∑ ( y t - βxt ) xt ∑ xt u t
= S= =
∂β σ2 σ2
vaø phöông sai cuûa noù laø ∑x2t/σ2 = Sxx/ σ2. Do ñoù,

2
z =
S2
=
(∑ xt ut ) ~ χ 2 2

Var(S) σ 2 S xx
1

Do ñoù, trò thoáng keâ kieåm ñònh LM ñöôïc cho bôûi
(∑ x u )
ˆ t t
2

LM = ~
σ 2 S xx
ˆ
Haõy xem xeùt hoài qui phuï ut = γxt + vt. Laøm theo caùc böôùc gioáng nhö ví duï 6.A.1, deã daøng coù
ñöôïc caùc phöông trình sau:

ˆ ∑ t t, ∑ ut 2
xu ˆ ~ ˆ
γ= RSS aux = γ ∑ xt u t ,
ˆ ˆ σ2 =
S xx n
Thay theá caùc bieåu thöùc naøy vaøo trò thoáng keâ kieåm ñònh LM, chuùng ta coù

[
LM = n RSS aux (∑ u )] = n[RSS
ˆ 2
t aux TSS aux ] = nRaux
2



Ñieàu naøy taïo ra keát quaû ñaõ ñöôïc cho trong taøi lieäu raèng trò thoáng keâ kieåm ñònh LM baèng soá
quan saùt nhaân vôùi R2 chöa hieäu chænh cuûa hoài qui phuï. Maëc duø chöùng minh naøy chæ cho tröôøng
hôïp hoài qui ñôn ñöôïc xem xeùt ôû ñaây, nhöng noù cuõng ñuùng cho moâ hình hoài qui boäi toång quaùt.
Muoán bieát theâm chi tieát, haõy xem Ramanathan (1993), trang 276-278.


Rama Ch6

More Related Content

Similar to Rama Ch6

More from Vince Vo

Recently uploaded

Rama Ch6