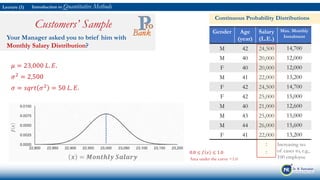
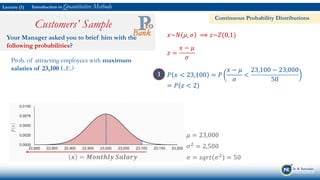
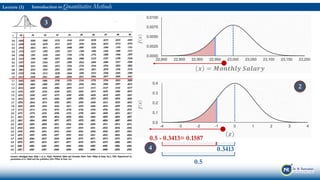
The document is an introduction to quantitative methods focusing on random variables and probability distributions, particularly in analyzing customer data for an insurance department. It discusses how to select a sample from VIP customers, collect relevant data, and calculate important statistical measures such as age distribution, mean, and variance. Key references and notable quotes are included to reinforce the learning process.

1. Quantitative Methods
Dr. Mohamed Ramadan
Moh_Ramadan@icloud.com

2. Quantitative Methods
Introduction to
Quantitative Methods
Lecture (1)

3. Lecture (1)
References
Introduction to Quantitative Methods
Key Reference:
Keller, Gerald (2012). Managerial Statistics (9th ed.). South Western, CENGAGE Learning.
Important Readings:
Brett Davies, M. (2007). Doing a Successful Research Project; Using Qualitative or Quantitative Methods.
Palgrave MacMillan.
Cresswell, J (2008). Research Design: Qualitative, Quantitative and Mixed Methods Approaches. Sage
Publications.
Silverman, D (2009). Doing Qualitative Research. Sage Publications.
Keller G. (2010). Managerial Statistics Abbreviated (8th ed.). International Edition, South Western College
Ghauri, P. and Gronhaugh, K. (2005). Research Methods in Business Studies: A Practical Guide. Pearson
Education Ltd.

4. Muhammad Ali
❝I hated every
minute of training,
but I said, Don’t
quit.
Suffer now and
live the rest of
your life as a
champion❞

5. Lecture (1)
Random Variables and Probability Distributions
Introduction to Quantitative Methods
Customers’ Sample
Suppose that you are working in the insurance
department at Pro-Bank ... Your manager asked you
to select a random sample from the VIP
customers, in the age group 40-45 years, whom are
working in company X, which is an about 10
customers. Moreover, he asked you to collect their
Age, Gender and Monthly Salary.
M
42 year
24,500
L.E.
M
40 year
20,000
L.E.
F
40 year
20,000
L.E.
M
41 year
22,000
L.E.
F
42 year
24,500
L.E.
F
42 year
25,000
L.E.
M
40 year
21,000
L.E.
M
43 year
25,000
L.E.
M
44 year
26,000
L.E.
F
41 year
22,000
L.E.
Gender Age (year) Salary (L.E.)
M 42 24,500
M 40 20,000
F 40 20,000
M 41 22,000
F 42 24,500
F 42 25,000
M 40 21,000
M 43 25,000
M 44 26,000
F 41 22,000
Variables

6. Lecture (1)
Random Variables and Probability Distributions
Customers’ Sample
Suppose that you are working in the insurance
department at Pro-Bank ... Your manager asked you
to select a random sample from the VIP
customers, in the age group 40-45 years, whom are
working in company X, which is an about 10
customers. Moreover, he asked you to collect their
Age, Gender and Monthly Salary.
M
42 year
24,500
L.E.
M
40 year
20,000
L.E.
F
40 year
20,000
L.E.
M
41 year
22,000
L.E.
F
42 year
24,500
L.E.
F
42 year
25,000
L.E.
M
40 year
21,000
L.E.
M
43 year
25,000
L.E.
M
44 year
26,000
L.E.
F
41 year
22,000
L.E.
What is a Random Variable?
❝is a function or rule
that assigns a value to
each outcome of an
experiment.❞
Introduction to Quantitative Methods

7. Lecture (1)
Random Variables and Probability Distributions
Customers’ Sample
Suppose that you are working in the insurance
department at Pro-Bank ... Your manager asked you
to select a random sample from the VIP
customers, in the age group 40-45 years, whom are
working in company X, which is an about 10
customers. Moreover, he asked you to collect their
Age, Gender and Monthly Salary.
M
42 year
24,500
L.E.
M
40 year
20,000
L.E.
F
40 year
20,000
L.E.
M
41 year
22,000
L.E.
F
42 year
24,500
L.E.
F
42 year
25,000
L.E.
M
40 year
21,000
L.E.
M
43 year
25,000
L.E.
M
44 year
26,000
L.E.
F
41 year
22,000
L.E.
Gender Age (year) Salary (L.E.) Max. Monthly
Instalment
M 42 24,500 14,700
M 40 20,000 12,000
F 40 20,000 12,000
M 41 22,000 13,200
F 42 24,500 14,700
F 42 25,000 15,000
M 40 21,000 12,600
M 43 25,000 15,000
M 44 26,000 15,600
F 41 22,000 13,200
Variables Max. Monthly Instalment
= 60% × Salary
Introduction to Quantitative Methods

8. Lecture (1)
Random Variables and Probability Distributions
Gender Age (year) Salary (L.E.) Max. Monthly
Instalment
M 42 24,500 14,700
M 40 20,000 12,000
F 40 20,000 12,000
M 41 22,000 13,200
F 42 24,500 14,700
F 42 25,000 15,000
M 40 21,000 12,600
M 43 25,000 15,000
M 44 26,000 15,600
F 41 22,000 13,200
Customers’ Sample
Your Manager asked you to brief him with age
distribution?
❝Discrete Random Variable is one that
can take on a countable number of
values.❞
❝Continuous Random Variable is one
which takes an infinite number of
possible values.❞
Introduction to Quantitative Methods

9. Lecture (1)
Random Variables and Probability Distributions
Gender Age (year) Salary (L.E.) Max. Monthly
Instalment
M 42 24,500 14,700
M 40 20,000 12,000
F 40 20,000 12,000
M 41 22,000 13,200
F 42 24,500 14,700
F 42 25,000 15,000
M 40 21,000 12,600
M 43 25,000 15,000
M 44 26,000 15,600
F 41 22,000 13,200
Customers’ Sample
Your Manager asked you to brief him with age
distribution?
Age
(year)
Frequency Distribution
40 3 3 ÷ 10= 0.3
41 2 2 ÷ 10= 0.2
42 3 3 ÷ 10= 0.3
43 1 1 ÷ 10= 0.1
44 1 1 ÷ 10= 0.1
Sum 10 1.0
0.0 ≤ 𝑃 𝑥 ≤ 1.0
'
!"" #
𝑃 𝑥 = 1.0
𝑥 𝑃 𝑥
Introduction to Quantitative Methods

10. Lecture (1)
Random Variables and Probability Distributions
Gender Age (year) Salary (L.E.) Max. Monthly
Instalment
M 42 24,500 14,700
M 40 20,000 12,000
F 40 20,000 12,000
M 41 22,000 13,200
F 42 24,500 14,700
F 42 25,000 15,000
M 40 21,000 12,600
M 43 25,000 15,000
M 44 26,000 15,600
F 41 22,000 13,200
Customers’ Sample
Your Manager asked you to brief him with age
distribution?
Age
𝒙
Frequency 𝑃 𝑥
40 3 0.3
41 2 0.2
42 3 0.3
43 1 0.1
44 1 0.1
Sum 10 1.0
Prob. of having customers less than 42
years old? 0.3 + 0.2 = 0.5
50%
Introduction to Quantitative Methods

11. Lecture (1)
Random Variables and Probability Distributions
Gender Age (year) Salary (L.E.) Max. Monthly
Instalment
M 42 24,500 14,700
M 40 20,000 12,000
F 40 20,000 12,000
M 41 22,000 13,200
F 42 24,500 14,700
F 42 25,000 15,000
M 40 21,000 12,600
M 43 25,000 15,000
M 44 26,000 15,600
F 41 22,000 13,200
Customers’ Sample
Your Manager asked you to brief him with age
distribution?
Age
𝒙
Frequency 𝑃 𝑥
40 3 0.3
41 2 0.2
42 3 0.3
43 1 0.1
44 1 0.1
Sum 10 1.0
Prob. of having customers by max. age of
42 years old? 0.3 + 0.2 + 0.3 = 0.8
80%
Introduction to Quantitative Methods

12. Lecture (1)
Random Variables and Probability Distributions
Gender Age (year) Salary (L.E.) Max. Monthly
Instalment
M 42 24,500 14,700
M 40 20,000 12,000
F 40 20,000 12,000
M 41 22,000 13,200
F 42 24,500 14,700
F 42 25,000 15,000
M 40 21,000 12,600
M 43 25,000 15,000
M 44 26,000 15,600
F 41 22,000 13,200
Customers’ Sample
Your Manager asked you to brief him with age
distribution?
Age
𝒙
Frequency 𝑃 𝑥
40 3 0.3
41 2 0.2
42 3 0.3
43 1 0.1
44 1 0.1
Sum 10 1.0
Prob. of having customers not less than 43
years old? 0.1 + 0.1 = 0.2
20%
Introduction to Quantitative Methods

13. Lecture (1)
Discrete Probability Distributions
Customers’ Sample
Your Manager asked you to brief him with Mean
and Variance of Age Distribution?
Age
𝒙
Frequency 𝑃 𝑥
40 3 0.3
41 2 0.2
42 3 0.3
43 1 0.1
44 1 0.1
Sum 10 1.0
𝜇 =
∑$%&
'
𝑥$
𝑁
= '
!"" #
𝑥𝑃 𝑥
𝜎( = '
!"" #
𝑥( 𝑃 𝑥 − 𝜇(
Population Mean:
Population Variance:
Introduction to Quantitative Methods

14. Lecture (1)
Customers’ Sample
Your Manager asked you to brief him with Mean
and Variance of Age Distribution?
Age
𝒙
Frequency 𝑃 𝑥 𝒙𝑃 𝑥 𝒙 𝟐 𝒙 𝟐 𝑃 𝑥
40 3 0.3 12 1600 480
41 2 0.2 8.2 1681 336.2
42 3 0.3 12.6 1764 529.2
43 1 0.1 4.3 1849 184.9
44 1 0.1 4.4 1936 193.6
Sum 10 1.0 41.5 8830 1723.9
𝜇 =
∑$%&
'
𝑥$
𝑁
= '
!"" #
𝑥𝑃 𝑥 = 41.5 𝑦𝑒𝑎𝑟𝑠
𝜎( = '
!"" #
𝑥( 𝑃 𝑥 − 𝜇( = 1723.9 − 41.5( = 1.7
Population Mean:
Population Variance:
1 2 3
4
5
Discrete Probability Distributions
Introduction to Quantitative Methods
𝜎 = 𝑠𝑞𝑟𝑡 𝜎( = 𝑠𝑞𝑟𝑡 1.7 = 1.3 𝑦𝑒𝑎𝑟𝑠

15. Lecture (1)
0.0 ≤ 𝑓 𝑥 ≤ 1.0
Increasing no.
of cases to, e.g.,
100 employee
Gender Age
(year)
Salary
(L.E.)
Max. Monthly
Instalment
M 42 24,500 14,700
M 40 20,000 12,000
F 40 20,000 12,000
M 41 22,000 13,200
F 42 24,500 14,700
F 42 25,000 15,000
M 40 21,000 12,600
M 43 25,000 15,000
M 44 26,000 15,600
F 41 22,000 13,200
:
:
Area under the curve =1.0
Continuous Probability Distributions
Customers’ Sample
Your Manager asked you to brief him with
Monthly Salary Distribution?
𝜇 = 23,000 𝐿. 𝐸.
𝜎( = 2,500
𝜎 = 𝑠𝑞𝑟𝑡 𝜎( = 50 𝐿. 𝐸.
𝒙 = 𝑴𝒐𝒏𝒕𝒉𝒍𝒚 𝑺𝒂𝒍𝒂𝒓𝒚
𝒇𝒙
Introduction to Quantitative Methods

16. Lecture (1)
Continuous Probability Distributions
Customers’ Sample
Your Manager asked you to brief him with the
following probabilities?
𝜇 = 23,000
𝜎( = 2,500
𝜎 = 𝑠𝑞𝑟𝑡 𝜎( = 50
Prob. of attracting employees with maximum
salaries of 23,100 L.E.?
𝑥~𝑁 𝜇, 𝜎 ⟹ 𝑧~𝑍(0,1)
𝒙 = 𝑴𝒐𝒏𝒕𝒉𝒍𝒚 𝑺𝒂𝒍𝒂𝒓𝒚
𝒇𝒙
𝑃 𝑥 < 23,100 = 𝑃
𝑥 − 𝜇
𝜎
<
23,100 − 23,000
50
= 𝑃 𝑧 < 2
𝑧 =
𝑥 − 𝜇
𝜎
1
Introduction to Quantitative Methods

17. Lecture (1)
𝒙 = 𝑴𝒐𝒏𝒕𝒉𝒍𝒚 𝑺𝒂𝒍𝒂𝒓𝒚
𝒇𝒙
𝒛
3
𝒇𝒛
2
𝑃 𝑥 < 23,100 = 𝑃 𝑧 < 2 = 0.5 + 0.4772
= 0.98
4
0.5 0.4772
Introduction to Quantitative Methods

18. Lecture (1)
Continuous Probability Distributions
Customers’ Sample
Your Manager asked you to brief him with the
following probabilities?
𝜇 = 23,000
𝜎( = 2,500
𝜎 = 𝑠𝑞𝑟𝑡 𝜎( = 50
Prob. of attracting employees with maximum
salaries of 22,950 L.E.?
𝑥~𝑁 𝜇, 𝜎 ⟹ 𝑧~𝑍(0,1)
𝒙 = 𝑴𝒐𝒏𝒕𝒉𝒍𝒚 𝑺𝒂𝒍𝒂𝒓𝒚
𝒇𝒙
𝑃 𝑥 < 22,950 = 𝑃
𝑥 − 𝜇
𝜎
<
22,950 − 23,000
50
= 𝑃 𝑧 < −1
𝑧 =
𝑥 − 𝜇
𝜎
1
Introduction to Quantitative Methods

19. 𝒙 = 𝑴𝒐𝒏𝒕𝒉𝒍𝒚 𝑺𝒂𝒍𝒂𝒓𝒚
Lecture (1)
𝒇𝒙
𝒛
𝒇𝒛
2
3
0.5
0.3413
0.5 - 0.3413= 0.1587
4
Introduction to Quantitative Methods

20. Lecture (1)
𝒛
𝒇𝒛
2
3
0.5 - 0.3413= 0.1587
4
𝑃 𝑥 < 22,950 = 𝑃 𝑧 < −1 = 0.5 − 0.3413
= 0.1587 ≅ 0.16
5
0.5
0.3413
Introduction to Quantitative Methods

21. Frank Sinatra
❝Wake up
to reality❞