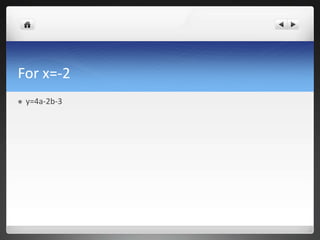
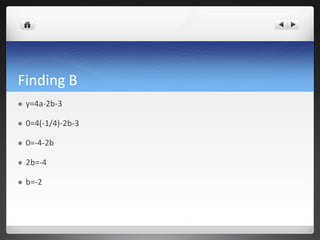
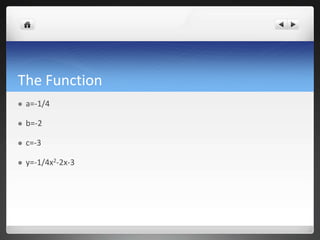
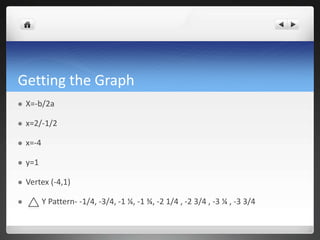
The document discusses exploring the quadratic function y=-1/4x^2 - 2x - 3. It goes through the process of determining the intercepts, finding the coefficients a, b, and c by setting the function equal to the intercepts and solving the resulting system of equations. This gives a=-1/4, b=-2, and c=-3. It then discusses finding the vertex at (-4,1) and graphing the parabola. Finally, it shows solving the quadratic equation using three methods - the quadratic formula, completing the square, and factoring - to find the x-intercepts of -2 and -6.

1. Exploring Quadratic Functions

2. The Intercepts
The given intercepts:
x intercepts=-6,-2
y intercept= -3

3. The Quadratic Function
 y=ax2+bx+c
 For x=-6
 y=a(-6)2+b(-6)-3
 For x=-2
 y=a(-2)2+b(-2)-3

4. For x=-6
 y=36a-6b-3
 Y=-12a+2b+1

5. For x=-2
 y=4a-2b-3

6. Together
 Y=-12a+2b+1
 y=4a-2b-3
 0=-8a-2
 8a=-2
 a=-1/4

7. Finding B
 y=4a-2b-3
 0=4(-1/4)-2b-3
 0=-4-2b
 2b=-4
 b=-2

8. The Function
 a=-1/4
 b=-2
 c=-3
 y=-1/4x2-2x-3

9. Getting the Graph
 X=-b/2a
 x=2/-1/2
 x=-4
 y=1
 Vertex (-4,1)
 Y Pattern- -1/4, -3/4, -1 ¼, -1 ¾, -2 1/4 , -2 3/4 , -3 ¼ , -3 3/4

10. The Graph

11. Solve!
 y=-1/4x2-2x-3
 x=(-b+- b2-4ac )/2a
 x=2+- 4-3 /-1/2
 2+-1/-1/2
 X=-2 or -6

12. Completing the Square
 y=-1/4x2-2x-3
 x2+8x+12=0
 x2+8x+16=4
 (x+4)2=4
 X+4=+-2
 X=-2 or -6

13. Factoring
 y=-1/4x2-2x-3
 x2+8x+12=0
 (x+2)(x+6)=0
 X+2=0
 X+6=0
 X=-2 or -6

14. Thank You For Watching!