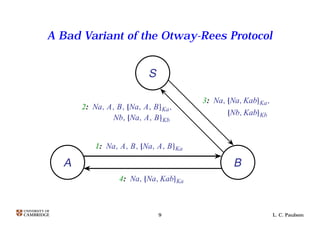
This document discusses modeling security protocols and proving their properties formally. It describes an operational model that uses traces of events and defines functions over messages to represent encryption and decryption. Properties like authentication and secrecy are modeled as safety properties over these traces. The model supports inductive proofs of protocols and has been used to verify real-world protocols like TLS, though the level of abstraction must be carefully chosen based on the questions being asked.

1. Proving Security Protocols Correct
Lawrence C. Paulson
Computer Laboratory

2. How Detailed Should a Model Be?
too detailed
too simple
concrete abstract
not usable not credible
``proves''
everything
``attacks''
everything
publications
1 L. C. Paulson

3. Case Study: the Plight of Monica and Bill
2 L. C. Paulson

4. A,Na,Sid,Pa
client server
client hello
Nb,Sid,Pb
server hello
cert(B,Kb)
server certificate
cert(A,Ka)
client certificate
{PMS}Kb
client key exchange
-1
{Hash(Nb,B,PMS)}Ka
certificate verify
M = PRF(PMS,Na,Nb)
Finished = Hash(M,messages)
{Finished}clientK(Na,Nb,M)
client finished
{Finished}serverK(Na,Nb,M)
server finished
An Internet Security
Protocol (TLS)
3 L. C. Paulson

5. Why Are Security Protocols Often Wrong?
they are TRIVIAL programs built from simple
primitives, BUT they are complicated by
concurrency
a hostile environment
– a bad user controls the network
obscure concepts
vague specifications
– we have to guess what is wanted
4 L. C. Paulson

6. Typical Protocol Goals
Authenticity: who sent it?
Integrity: has it been altered?
Secrecy: who can receive it?
Anonymity
Non-repudiation : : :
all SAFETY properties
5 L. C. Paulson

7. What Are Session Keys?
used for a single session
not safeguarded forever
distributed using long-term keys
could eventually become compromised
can only be trusted if FRESH
6 L. C. Paulson

8. Freshness, or Would You Eat This Fish?
wine: six years old
fish: ? weeks old
7 L. C. Paulson

9. Packaging a Session Key for Bill
fjK; A; NbjgKb
session key
person it's
shared with nonce specified
sealed using
Bill's key
by Bill:
proof of freshness
8 L. C. Paulson

10. A Bad Variant of the Otway-Rees Protocol
3: Na; fjNa; KabjgKa;
fjNb; KabjgKb
1: Na; A; B; fjNa; A; BjgKa
B
S
A
2: Na; A; B; fjNa; A; BjgKa;
Nb; fjNa; A; BjgKb
4: Na; fjNa; KabjgKa
9 L. C. Paulson

11. A Splicing Attack with Interleaved Runs
1: A !CB : Na; A; B; fjNa; A; BjgKa
10
: C ! A : Nc;C; A; fjNc;C; AjgKc
20
: A !CS : Nc;C; A; fjNc;C; AjgKc; Na0
; fjNc;C; AjgKa
200
: CA ! S : Nc;C; A; fjNc;C; AjgKc; Na; fjNc;C; AjgKa
30
: S !CA : Nc; fjNc; KcajgKc; fjNa; KcajgKa
4: CB ! A : Na; fjNa; KcajgKa
Alice thinks the key Kca is shared
with Bill, butÊit's shared with Carol!
10 L. C. Paulson

12. A Bad Variant of the Yahalom Protocol
2: B; Nb; fjA; NajgKb
B
S
3: fjB; Kab; Na; NbjgKa;
fjA; KabjgKb
A
1: A; Na
4: fjA; KabjgKb; fjNbjgKab
11 L. C. Paulson

13. A Replay Attack
1: CA ! B : A; Nc
2: B !CS : B; Nb; fjA; NcjgKb
4: CA ! B : fjA; Kjg
Kb; fjNbjgK
Carol has broken the old key, K. She
makes Bill think it is shared with Alice.
12 L. C. Paulson

14. Verification Method I: Authentication Logics
BAN logic: Burrows, Abadi, Needham (1989)
Short proofs using high-level primitives:
Nonce N is fresh
Key Kab is good
Agent S can be trusted
good for freshness
not-so-good for secrecy or splicing attacks
13 L. C. Paulson

15. Verification Method II: State Enumeration
Specialized tools (Meadows)
General model-checkers (Lowe)
Model protocol as a finite-state system
automatically finds splicing attacks
freshness is hard to model
Try using formal proof!
14 L. C. Paulson

16. Why An Operational Model?
good fit to informal protocol proofs: inductive
simple foundations
readable protocol specifications
easily explained to security experts
easily mechanized using Isabelle
15 L. C. Paulson

17. An Overview of Isabelle
uses higher-order logic as a logical framework
generic treatment of inference rules
logics supported include ZF set theory HOL
powerful simplifier classical reasoner
strong support for inductive definitions
16 L. C. Paulson

18. Overview of the Model
Traces of events
– A sends B message X
– A receives X
– A stores X
A powerful attacker
– is an accepted user
– attempts all possible splicing attacks
– has the same specification in all protocols
17 L. C. Paulson

19. Agents and Messages
agent A; B; : : : D Server j Friend i j Spy
message X; Y; : : : D Agent A
j Nonce N
j Key K
j fjX; X0jg compound message
j Crypt K X
free algebras: we assume PERFECT ENCRYPTION
18 L. C. Paulson

20. Functions over Sets of Messages
parts H: message components
Crypt K X7! X
analz H: accessible components
Crypt K X; K−17! X
synth H: expressible messages
X; K7! Crypt K X
RELATIONS are traditional, but FUNCTIONS give us
an equational theory
19 L. C. Paulson

21. Operational Definition: analz H
Crypt K X 2 analzH K−1 2 analz H
X 2 analz H
X 2 H
X 2 analz H
fjX; Y jg 2 analz H
X 2 analz H
fjX; Y jg 2 analz H
Y 2 analz H
Typical derived law:
analz G [ analz H analz.G [ H/
20 L. C. Paulson

22. Operational Definition: synth H
X 2 H
X 2 synth H
Agent A 2 synth H
X 2 synthH Y2 synth H
fjX; Y jg 2 synth H
X 2 synthH K2 H
Crypt K X 2 synth H
agent names can be guessed
nonces keys cannot be!
21 L. C. Paulson

23. A Few Equations
parts.parts H/ D parts H transitivity
analz.synth H/ D analz H [ synth H “cut elimination”
Symbolic Evaluation:
analz.fCrypt K Xg [ H/ D
8
fCrypt K Xg [ analz.fXg [ H/ if K−1 2 analz H
fCrypt K Xg [ analz H otherwise
:
22 L. C. Paulson

24. What About Freshness?
23 L. C. Paulson

25. Modelling Attacks and Key Losses
If X 2 synth.analz.spies evs//
may add Says Spy B X (Fake rule)
If the server distributes session key K
may add Notes Spy fjNa; Nb; Kjg (Oops rule)
Nonces show the TIME of the loss
24 L. C. Paulson

26. Overview of Results
facts proved by induction classical reasoning
simplifying analz H: case analysis, big formulas
handles REAL protocols: TLS, Kerberos, : : :
lemmas reveal surprising protocol features
failed proofs can suggest attacks
Proofs require days or weeks of effort
Generalizing induction formulas is hard!
25 L. C. Paulson

27. The Recursive Authentication Protocol
designed in industry (APM Ltd)
novel recursive structure: variable length
VERIFIED by Paulson
– assuming perfect encryption
ATTACKED by Ryan and Schneider
– using the specified encryption (XOR)
Doesn’t proof give certainty? Not in the real world!
26 L. C. Paulson

28. So Then, How Detailed Should a Model Be?
detailed enough to answer the relevant
questions
abstract enough to fit our budget
model-checking is almost free
(thanks to Lowe, Roscoe, Schneider)
formal proofs give more, but cost more
27 L. C. Paulson

29. Don’t let theory displace reality