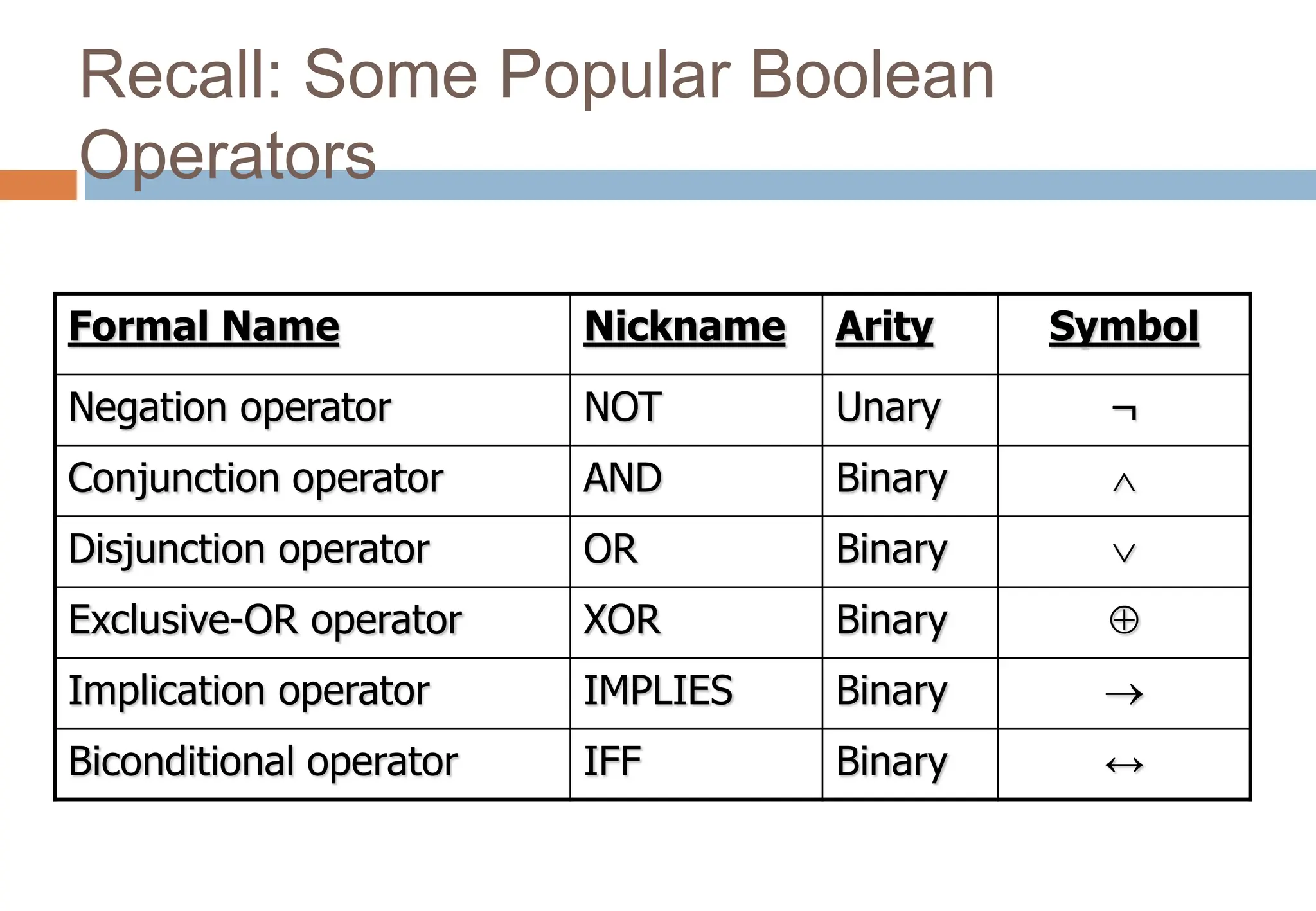
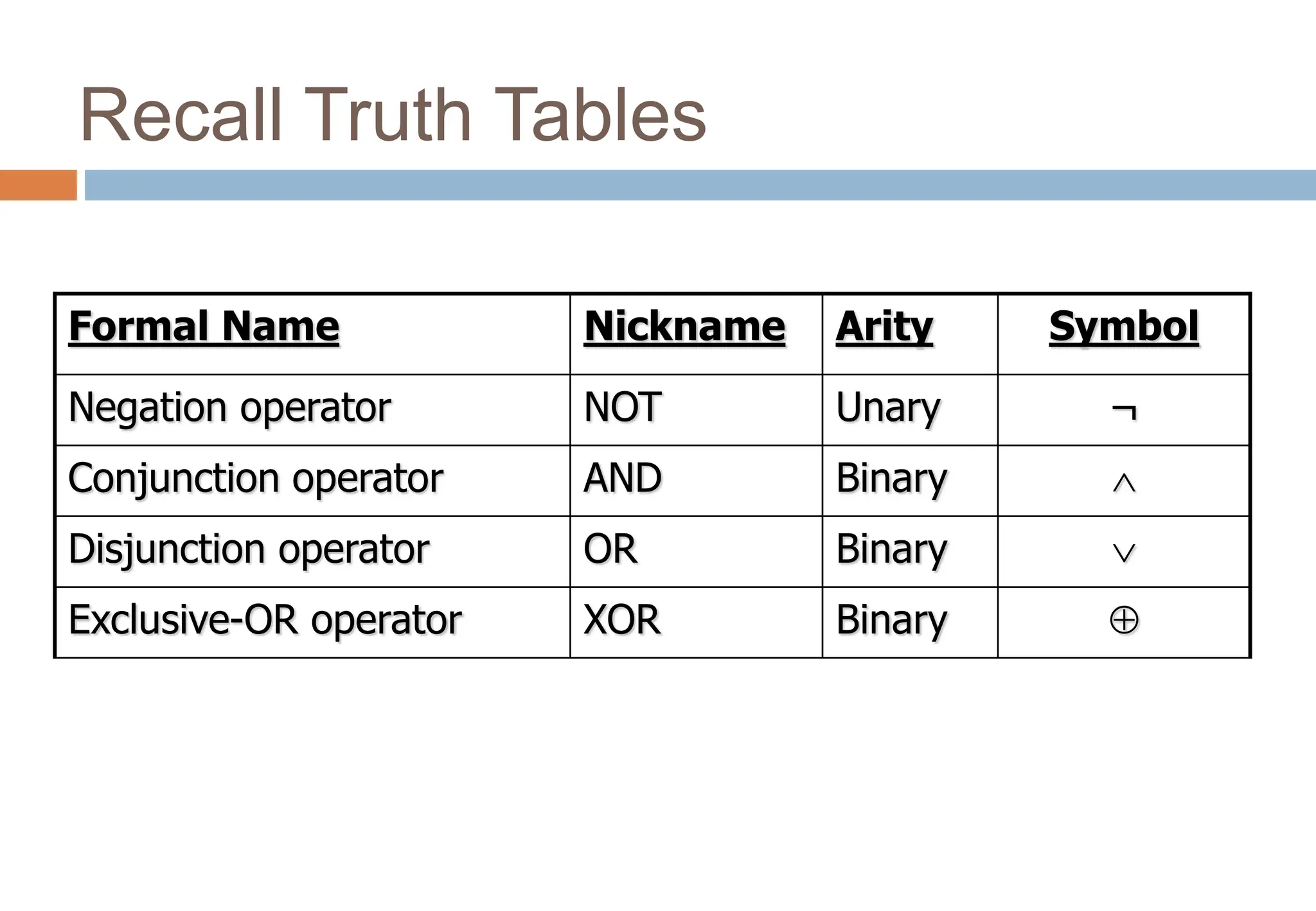
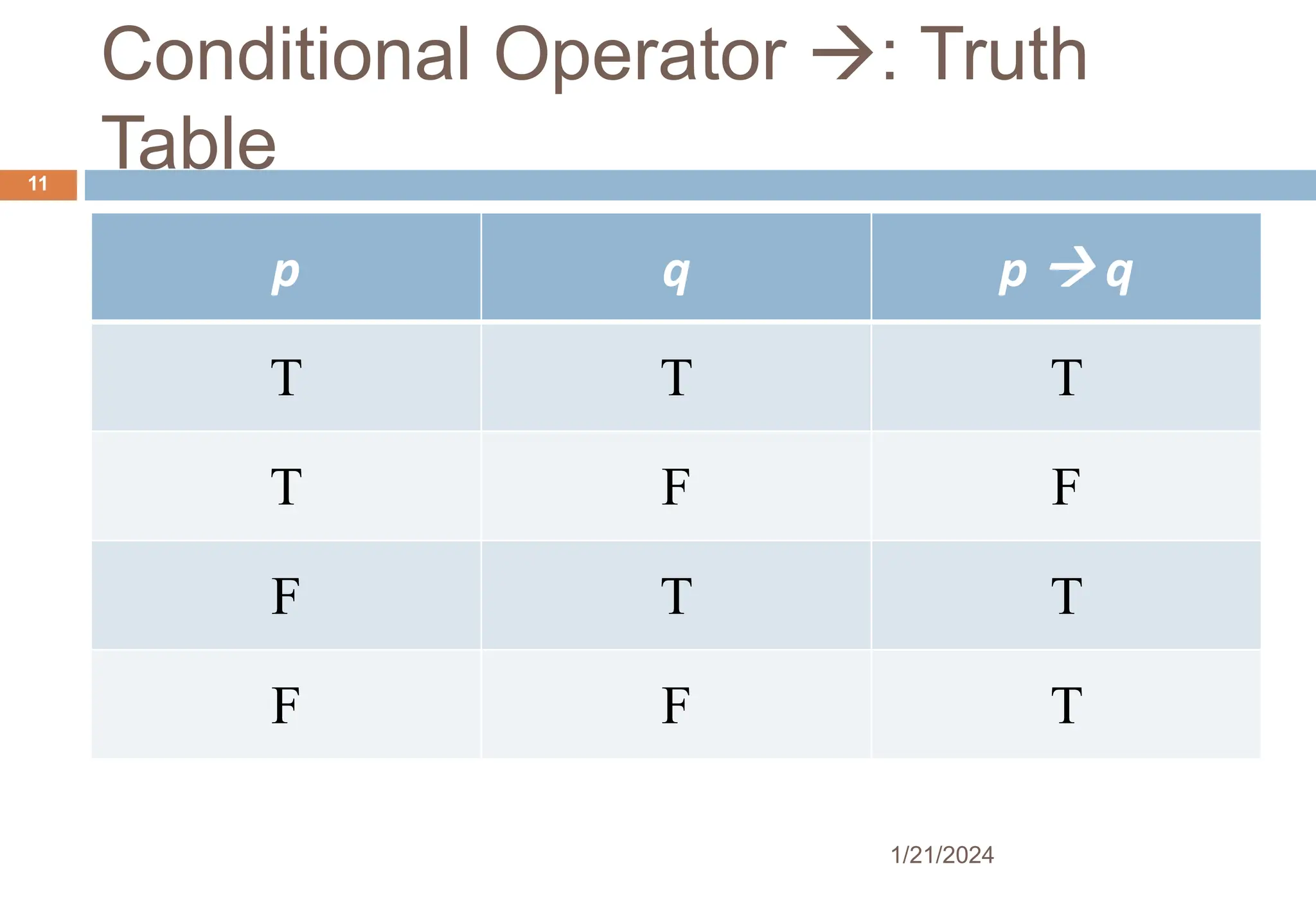
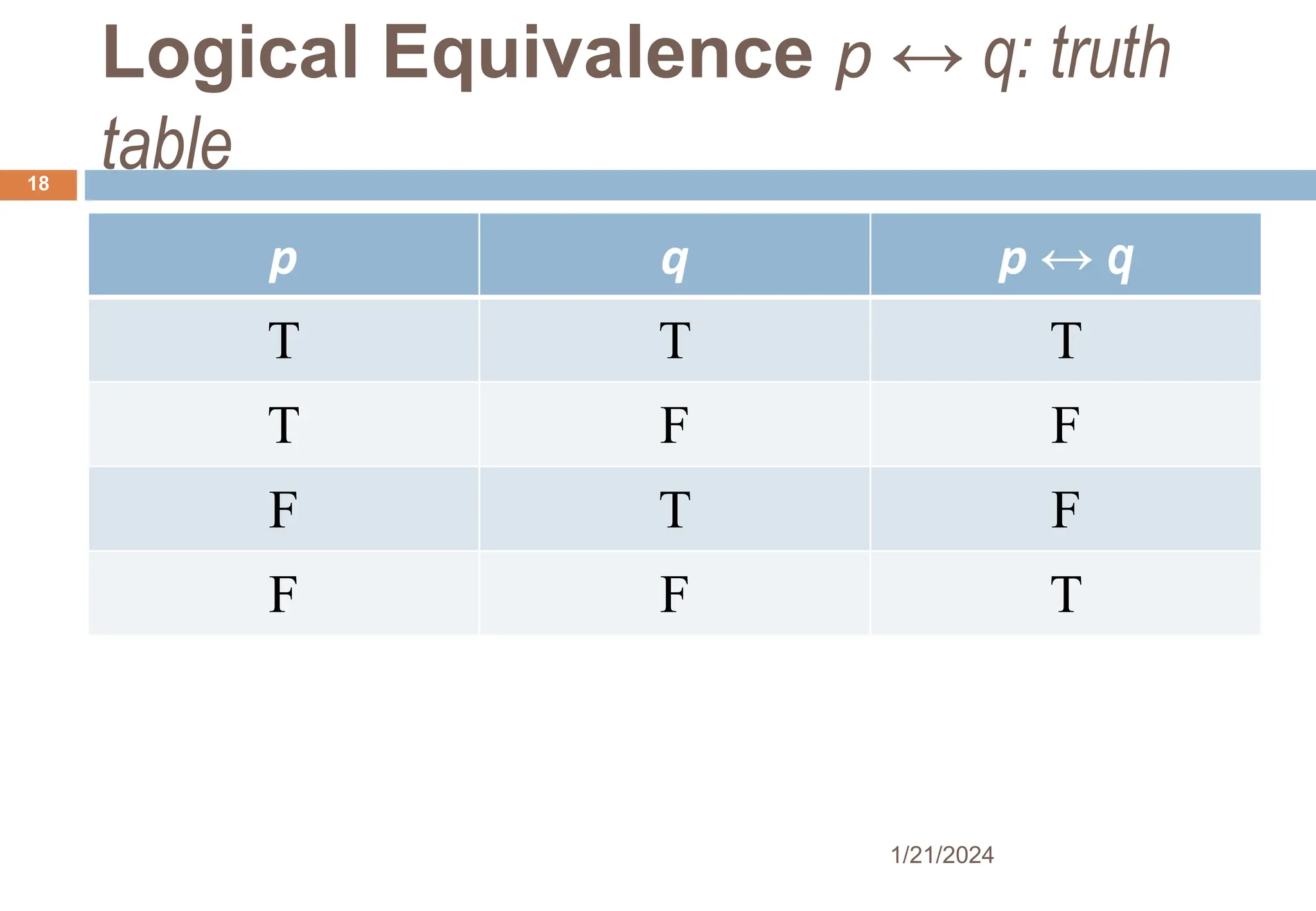
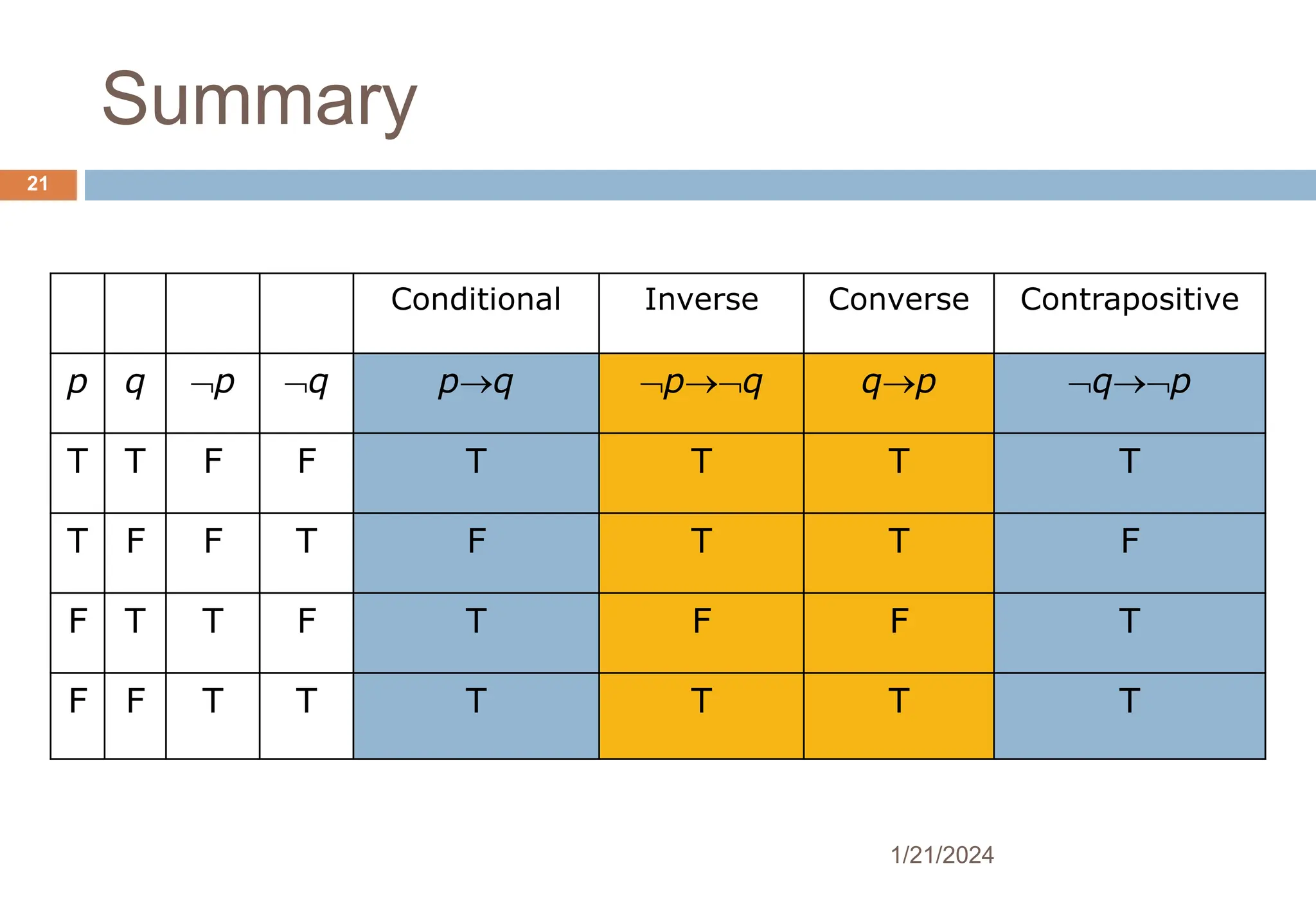
1) The document discusses foundational concepts in propositional logic, including logical form, statements, connectives, and truth tables. 2) It introduces common logical operators such as negation, conjunction, disjunction, implication, equivalence, and explains how to translate sentences between English and symbolic logic. 3) Conditional statements and their contrapositives, converses and inverses are defined. It is shown that a conditional statement is logically equivalent to its contrapositive using truth tables.

1. Foundations of Logic
1.1

2. Logic of Statements
 Logical Form
 Conditional statement
 Logical Equivalence

3. Recall: Logical Form
 Statement (proposition)
 is a sentence that is true or false but not both
 Connectives
 And, or, xor,…
 Compound statement
 is a statement built out of simple statements using
logical operations or connectives: negation,
conjunction, disjunction

4. Recall: Some Popular Boolean
Operators
Formal Name Nickname Arity Symbol
Negation operator NOT Unary ¬
Conjunction operator AND Binary 
Disjunction operator OR Binary 
Exclusive-OR operator XOR Binary 
Implication operator IMPLIES Binary 
Biconditional operator IFF Binary ↔
Topic #1.0 – Propositional Logic: Operators

5. Recall Truth Tables
Formal Name Nickname Arity Symbol
Negation operator NOT Unary ¬
Conjunction operator AND Binary 
Disjunction operator OR Binary 
Exclusive-OR operator XOR Binary 
Topic #1.0 – Propositional Logic: Operators

6. Recall: Translating Sentences to
Propositional logic
Problem: Translate the following sentence into
propositional logic:
“If you can access the Internet from campus only if
you are a computer science major or you are not a
freshman.”
One Solution: Let a, c, and f represent
respectively “You can access the internet from
campus,” “You are a computer science major,” and
“You are a freshman.”  
a c f
  

7. Tips for Translating English Sentences
Steps to convert an English sentence to a
statement in propositional logic
• Identify atomic propositions and represent using
propositional variables.
• Determine appropriate logical connectives
“If I go to Harry’s or to the country, I will not
go shopping.”
• p: I go to Harry’s
• q: I go to the country.
• r: I will go shopping.
If p or q then not r.
 
p q r
  

8. Logic of Statements
 Logical Form
 Conditional statement
 Logical Equivalence

9. Conditional Operator 
 You play football in the evening, if you study in the afternoon.
 p=you study in the afternoon
 q=you play football in the evening
 The order of p and q is important, what is it?
 p is the antecedent. q is the consequent.
 There are four possible outcomes of this:
 you study in the afternoon, and play football in the evening
(p is true and q is true)
 p q is true.

10. Conditional Operator 
 you study on the afternoon, but do not play football on the
evening (p is true and q is false)
 p  q is false. This means that, the condition (You play football on
the evening, if you study on the afternoon. ) is violated.
 you do not study on the afternoon, yet you play football on the
evening. (p is false and q is true)
 p q is true. The conditional statement (that You play football on
the evening, if you study on the afternoon.) has not been violated,
because violation only occurs if the antecedent is true.
 You do not play football on the evening, and you do not study
on the afternoon. (p is false and q is false)
 p q is true. The conditional statement (that You play football on
the evening, if you study on the afternoon. ) has not been violated,
because violation only occurs if the antecedent is true.
1/21/2024
10

11. Conditional Operator : Truth
Table
p q p  q
T T T
T F F
F T T
F F T
1/21/2024
11

12. Examples of Implications
 “If this lecture ever ends, then the sun will rise
tomorrow.” True or False?
 “If 2+1=6, then Rashed Elmajed is a singer.”
True or False?
 “If the moon is made of green cheese, then I will
never get old.” True or False?
Topic #1.0 – Propositional Logic: Operators

13. Converse, Inverse, Contrapositive
 Some terminology, for an implication p  q:
 Its converse is: q  p.
 Its inverse is: ¬p  ¬q.
 Its contrapositive: ¬q  ¬ p.
Topic #1.0 – Propositional Logic: Operators

14. Example on contrapositive and
converse
 Write down English sentences for the converse and the
contrapositive of: ‘If 250 is divisible by 4 then 250 is an even
number.’
 The sentence can be written as pq, where
 p denotes ‘250 is divisible by 4’
 and q denotes ‘250 is an even number’.
 The converse is q p, which we can write in English as
follows:
 ‘If 250 is an even number then 250 is divisible by 4.’
 The contrapositive is ¬q ¬p, which we write as follows:
 ‘If 250 is not an even number then 250 is not divisible by 4.’
 The Inverse? (Homework) 1/21/2024
14

15. Converse, Inverse, Contrapositive
 Some terminology, for an implication p  q:
 Its converse is: q  p.
 Its inverse is: ¬p  ¬q.
 Its contrapositive: ¬q  ¬ p.
 One of these three has the same meaning (same
truth table) as p  q. Can you figure out which?
Topic #1.0 – Propositional Logic: Operators

16. Logic of Statements
 Logical Form
 Conditional Statements
 Logical Equivalence

17. Logical Equivalence: p ↔ q
 The bi-conditional operator ↔ :
 It is called Logical Equivalence
 Also called if and only if
 Logical equivalence means that the truth values of two statements are the
same.
 This means that p ↔ q TRUE means that the truth values of p and q are
the same.
 When is the following an equivalence
 "You will see the magazine if and only if someone show it to you”
 If someone shows you the magazine and you see it, the statement is true.
 If someone shows you the magazine and you do not see it, the statement
is false because it is violated.
 If no one shows you the magazine and you see it, the biconditional
statement is false because it is violated.
 If no one shows you the magazine and you do not see it, the statement is
true.
1/21/2024
17

18. Logical Equivalence p ↔ q: truth
table
p q p ↔ q
T T T
T F F
F T F
F F T
1/21/2024
18

19. Contrapositive
 Is
p  q ↔ ¬q  ¬ p
How can we prove it?
 Homework: What about the converse?
1/21/2024
19

20. How do we know for sure?
 Proving the equivalence of p  q and its
contrapositive using truth tables:
p q q p pq q p
F F T T T T
F T F T T T
T F T F F F
T T F F T T
Topic #1.0 – Propositional Logic: Operators

21. Summary
1/21/2024
21
Conditional Inverse Converse Contrapositive
p q p q pq pq qp qp
T T F F T T T T
T F F T F T T F
F T T F T F F T
F F T T T T T T

22. Homework
 The bi-conditional statement ↔ is logically
equivalent to
1/21/2024
22

23. Boolean Operations Summary
 We have seen
1 unary operator and
5 binary operators
Their truth tables are below.
p q p pq pq pq pq pq
F F T F F F T T
F T T F T T T F
T F F F T T F F
T T F T T F T T
Topic #1.0 – Propositional Logic: Operators

24. Compound propositions
 Compound = More than one operation.
 Find truth table
 (pVq)(~p^ ~q)
Topic #1.0 – Propositional Logic: Operators

25. Nested Propositional Expressions
 Use parentheses to group sub-expressions:
“I just saw my old friend, and either he’s grown or
I’ve shrunk.”
 f  (g  s)
 (f  g)  s would mean something different
 f  g  s would be ambiguous
Topic #1.0 – Propositional Logic: Operators

26. Precedence of operators
 Just as in algebra, operators have precedence
 4+3*2 = 4+(3*2), not (4+3)*2
 Precedence order (from highest to lowest):
¬   → ↔
 The first three are the most important
 How to interpret: p  q  ¬r → s ↔ t
 yields: (p  (q  (¬r)) → s) ↔ (t)
 Not is always performed before any other
operation
1/21/2024
26

27. A Simple Exercise
 Let
p=“It rained last night”,
q=“The sprinklers came on last night,”
r=“The lawn was wet this morning.”
 Translate each of the following into English:
 ¬p =
 r  ¬p =
 ¬ r  p  q =
“It didn’t rain last night.”
“The lawn was wet this morning, and
it didn’t rain last night.”
“Either the lawn wasn’t wet this
morning, or it rained last night, or the
sprinklers came on last night.”
Topic #1.0 – Propositional Logic: Operators

28.  Ex. Prove that pq  (p  q).
p q p
p
q
q 
p
p 
q
q 
p
p 
 
q
q 
(
(
p
p 
 
q
q)
)
F F
F T
T F
T T
In class exercise: Proving
Equivalence
via Truth Tables
F
T
T
T
T
T
T
T
T
T
F
F
F
F
F
F
F
F
T
T
Topic #1.1 – Propositional Logic: Equivalences

29. Homework: Prove the following
 pT  p
 pF  F
 pp  p
 p  p
 (pq)r  p(qr)
 (pq)  p  q
 p  p  T p  p  F
Topic #1.1 – Propositional Logic: Equivalences

30. Homework 1.1
 4,10, 13, 14, 19, 25, 28, 29, 30, 31,33-41
 43
1/21/2024
30