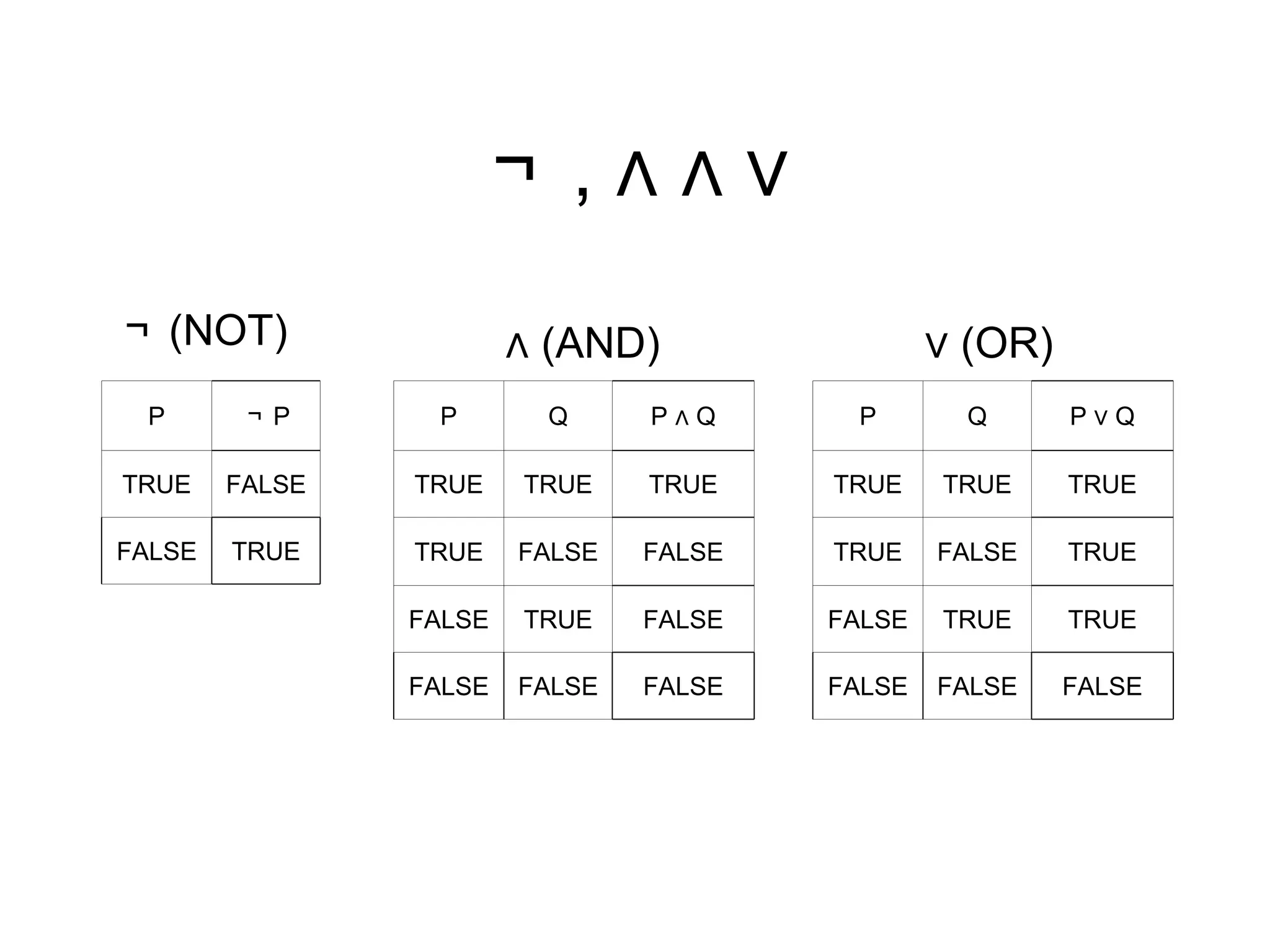
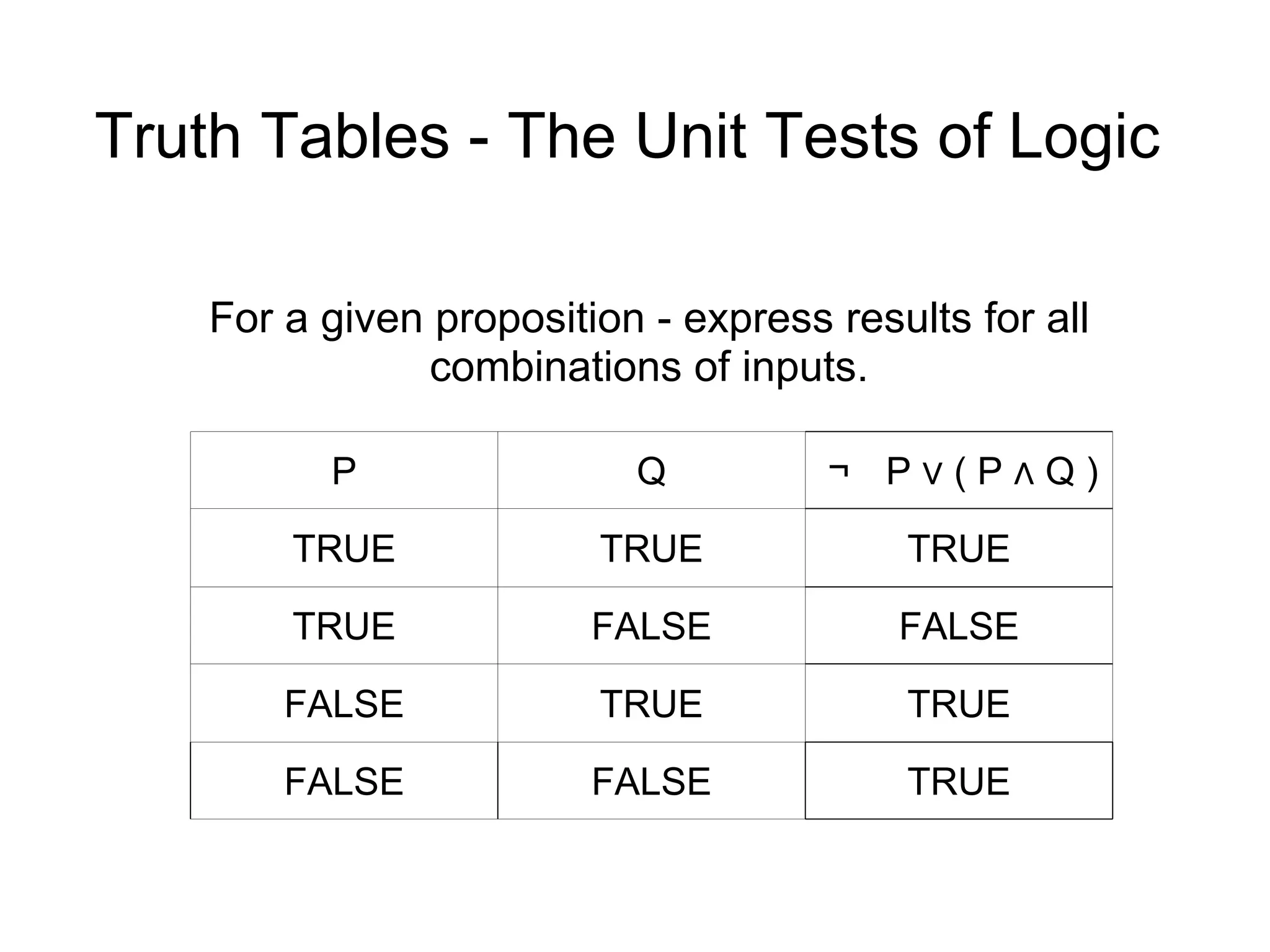
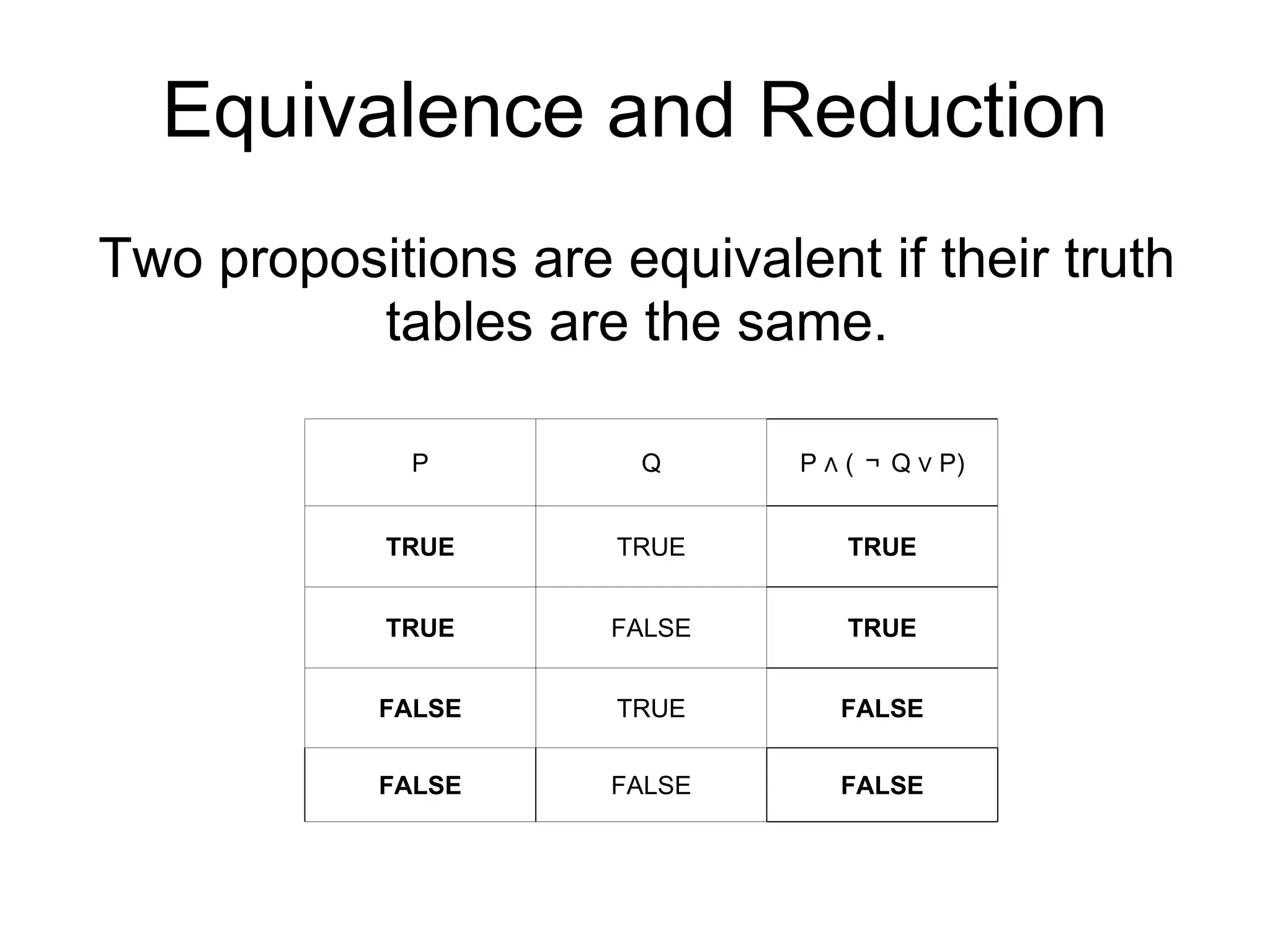
1) Propositional logic uses propositions that can be resolved as true or false and operators like NOT, AND, and OR to combine propositions. 2) Truth tables express all combinations of inputs to determine if a proposition is a tautology (always true) or contradiction (always false). 3) Equivalent propositions have the same truth values and De Morgan's laws can be used to transform expressions. 4) Some logical operators are "lazy" and short-circuit evaluation to improve efficiency by reducing unnecessary computations.

1. Propositional Logic for Programmers (or how I learnt to stop over-expressing and love the precedance)

2. Propositions Functions/Statements which can be resolved to True or False. P – Do you like Sausage Butties? Q – Do you like Bacon Butties[1]? [1] Technically Q is a tautology.

3. ￢ , ∧ ∧ ∨ ￢ (NOT) ∧ (AND) ∨ (OR) P Q P ∧ Q TRUE TRUE TRUE TRUE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE P Q P ∨ Q TRUE TRUE TRUE TRUE FALSE TRUE FALSE TRUE TRUE FALSE FALSE FALSE P ￢ P TRUE FALSE FALSE TRUE

4. Truth Tables - The Unit Tests of Logic For a given proposition - express results for all combinations of inputs. P Q ￢ P ∨ ( P ∧ Q ) TRUE TRUE TRUE TRUE FALSE FALSE FALSE TRUE TRUE FALSE FALSE TRUE

5. Tautologies Always true for any given input. Can usually be reduced to P v ¬P Contradiction - opposite of tautology. If not sure - check with a truth table.

6. P ∧ ( ￢ Q ∨ P)

7. Equivalence and Reduction Two propositions are equivalent if their truth tables are the same. P Q P ∧ ( ￢ Q ∨ P) TRUE TRUE TRUE TRUE FALSE TRUE FALSE TRUE FALSE FALSE FALSE FALSE

8. De Morgan's Law ￢ (P ∧ Q) === ￢ P ∨ ￢ Q ￢ (P ∨ Q) === ￢ P ∧ ￢ Q

9. Operational Cost Some operations *unavoidably* cost more than others to execute. Aim: Juggle evaluation order so lower cost operations are evaluated first and if possible reduce the number of calls to more expensive operations.

10. Eager and Lazy Operators Eager - Will evaluate both sides of expression. Lazy (Short Circuit) - Will only evaluate RHS of expression if will effect return. (Most developers use lazy without realising the full implication) Operator C-Standard Lazy C-Standard Eager ￢ (NOT) ! ! ∧ (AND) && & ∨ (OR) || |

11. Lazy & Side Effects class A { int _a; public awesome() { _a++; return true; } public freakin() { return true; } } a.awesome() && a.freakin() > true (A._a == 1) a.freakin() && a.awesome() > true (A._a == 0) Make sure you understand the side effects of methods before refactoring expressions.

12. Why we love && Fails where the first proposition is false. If we can organise with cheap, failing, first proposition - reduce the number of times expensive functions are called.

13. Why we love || Succeeds where the first proposition is true. Therefore - if we can express a statement with a cheap successful first proposition, then we limit the number of calls to second proposition.

14. Example var list = PopulateArray(); <-- populate a sparse 2d array. foreach(var item in list) { if ( ! (item == null || item.Contains(x))) { return &quot;awesome&quot;; } -- foreach(var item in list) { if ( item != null && ! item.Contains(x)) { return &quot;awesome&quot;; }

15. Summary The Essence of Discrete Mathematics, Neville Dean, ISBN: 0-13-345943-8 Kian Ryan http://www.kianryan.co.uk/