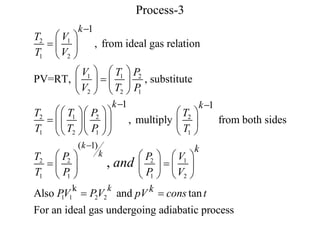
Thermodynamic processes involve a change in state of a system through heat or work interactions with the surroundings. Some common processes include: - Isothermal processes occur at constant temperature. For an ideal gas, heat and work are equal during these processes. - Isobaric processes occur at constant pressure. For an ideal gas, work done is equal to the pressure-volume area. - Adiabatic processes involve no heat transfer. For an ideal gas undergoing adiabatic changes, the pressure-volume ratio remains constant.

1. Thermodynamic Processes
• States of a thermodynamic system can be changed by
interacting with its surrounding through work and heat. When
this change occurs in a system, it is said that the system is
undergoing a process.
• A thermodynamic cycle is a sequence of different processes that
begins and ends at the same thermodynamic state.
• Some sample processes:
 Isothermal process: temperature is constant T=C
 Isobaric process: pressure is constant, P=C
 Isentropic process: entropy is constant, s=C
 Constant-volume process, v=C
 Adiabatic process: no heat transfer, Q=0

2. Process-1
• Use ideal gas assumption (closed system):
2
1
2 1
1 2
Isothermal process: T=constant
Energy balance U=Q-W, for ideal gas U= H=0
since both are functions of temperature only
Q=W, W= P
ln ln
Isobaric process:
mRT dV
dV dV mRT
V V
V P
mRT mRT
V P
  
 
   
 
   
   
  


2
2 1
1
2 1 2 1 2 1
2 2 1 1 2 1
P=constant
U=Q-W, W= PdV=P dV=P(V )
( ) ( ) ( )
( ) ( )
V
Q U P V V U U P V V
U PV U PV H H H
 
       
       
 

3. Process-2
v
v
Constant volume process: V=constant
Q-W= U, W= 0, no work done
Q= U=m u=m c
Adiabatic process: Q=0
Q-W= U, -W= U
- W=dU (infinitesimal increment of work and energy)
dU+PdV=0, mc 0
v
PdV
dT
mRT
dT dV
V
c

 
 
 
 
 
 
 




v
2 2 2 1 1
1 1 1 2 2
1
0, , integrate and assume
c =constant
ln ln ,
v
v
v
R k
c
c
RT dT dV
dT dV
V R T V
c T V T V V
R T V T V V

 
   
 
 
       
   
       
       

4. Process-3
2 1
1 2
1 1 2
2 2 1
2 1 2 2
1 2 1 1
2 2 2 1
1 1 1
( 1)
1
1 1
, from ideal gas relation
PV=RT, , substitute
, multiply from both sides
,
k
k
k
k k
T V
T V
V T P
V T P
T T P T
T T P T
T P P V
T P P
and


 
 
  
 
   

   
   
 
    
  
    
    
 
   
 
   
    2
1 1 2 2
k
Also and tan
For an ideal gas undergoing adiabatic process
k
k
k
V
PV PV pV cons t
 
 
 
 

5. Process-4
Polytropic Process: its P-V relation can be expressed as
PVn = constant, where n is a constant for a specific process
 Isothermal, T=constant, if the gas is an ideal gas then
PV=RT=constant, n=1
 Isobaric, P=constant, n=0 (for all substances)
 Constant-volume, V=constant, V=constant(P)(1/n), n=
(for all substances)
 Adiabatic process, n=k for an ideal gas
1 1 2 2
2 2
1 1
1 1
2
1 1
1 1 2 2 1 1
1 1 2 1
1
( )
( )
( ) ( )
1 1
n n n
n n
n
n n n n
PV PV PV
W PdV PV V dV
PV PV PV
PV V dV V V
n n

  
 
 

   
 
 
