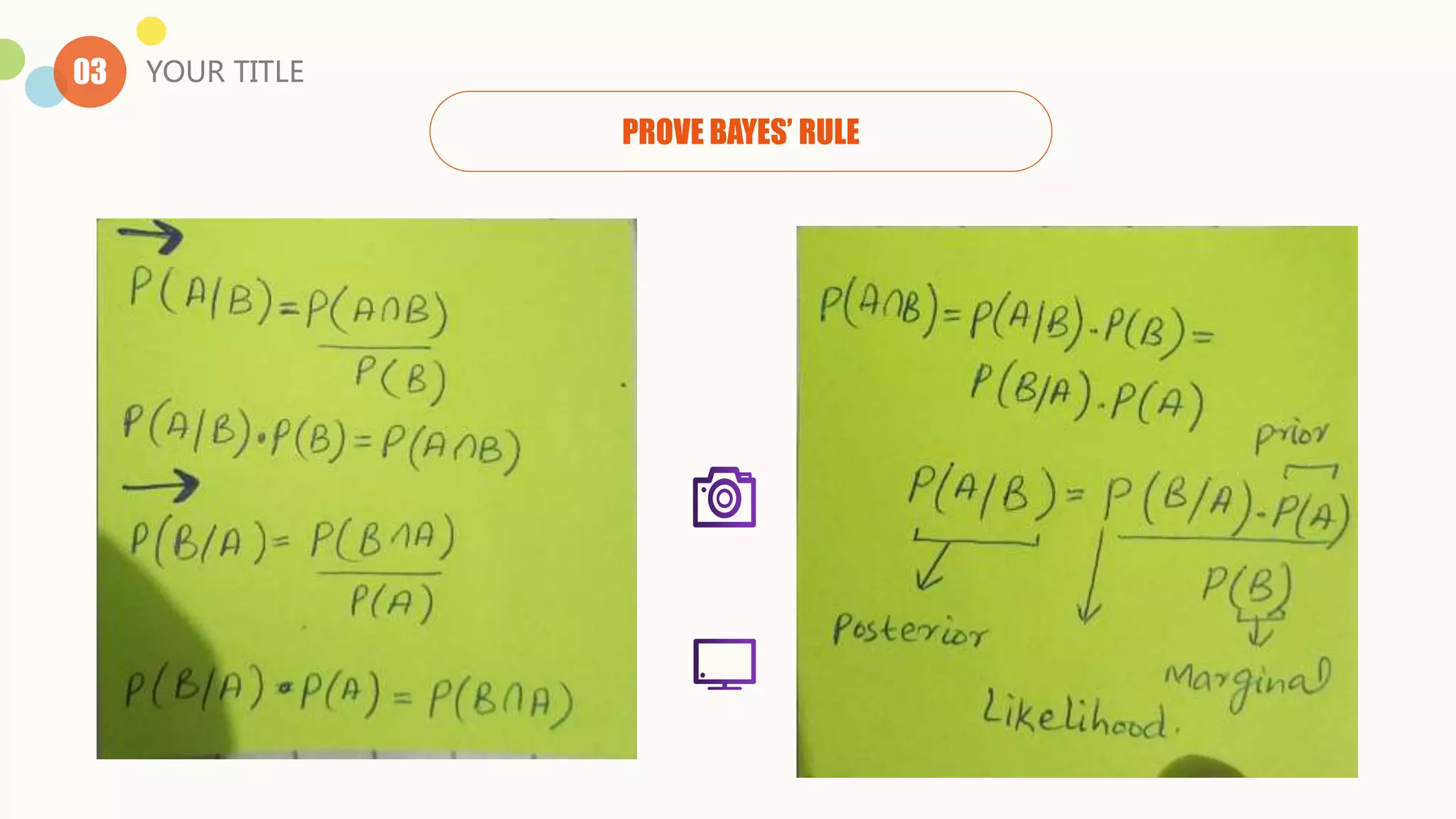
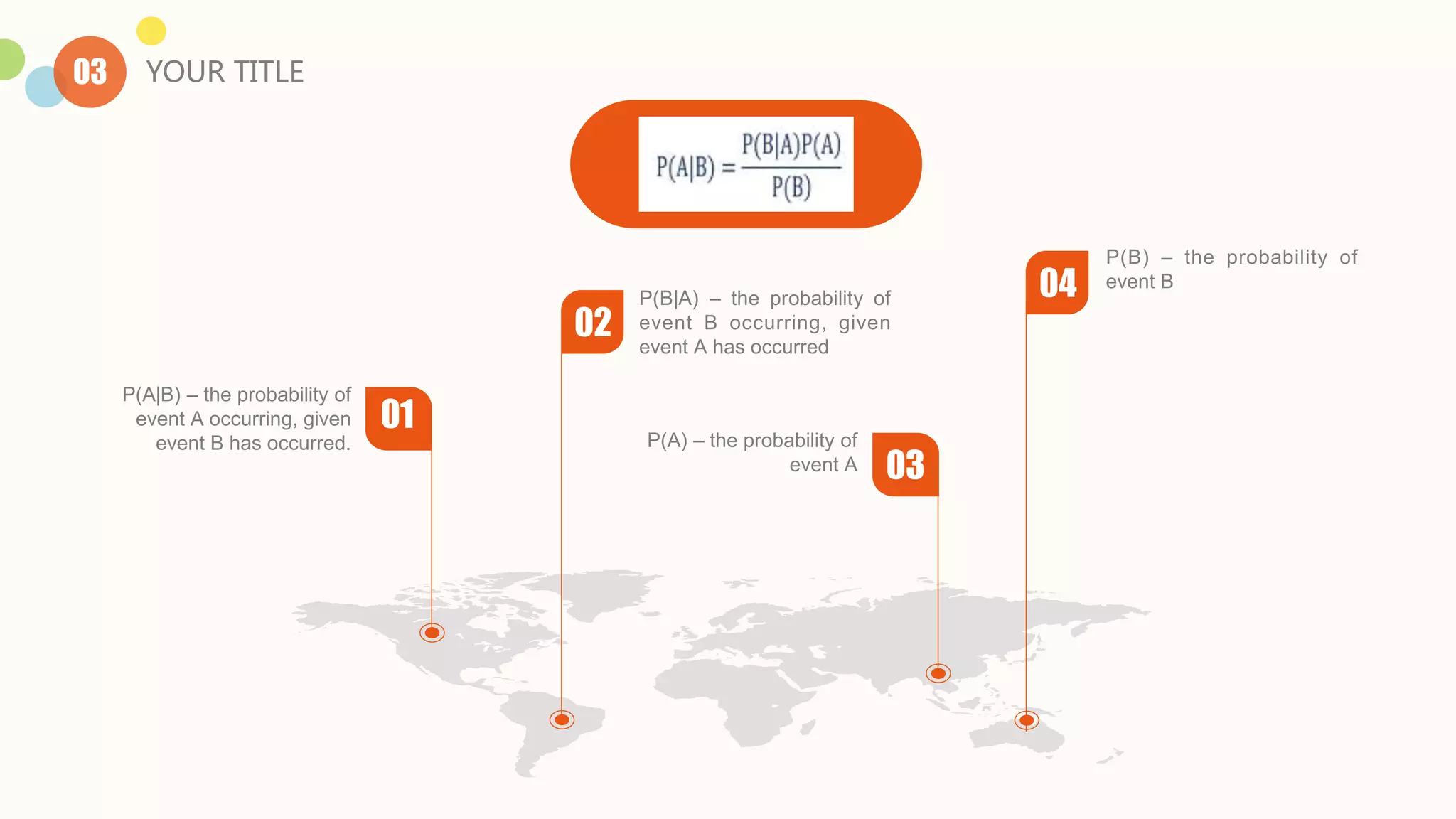
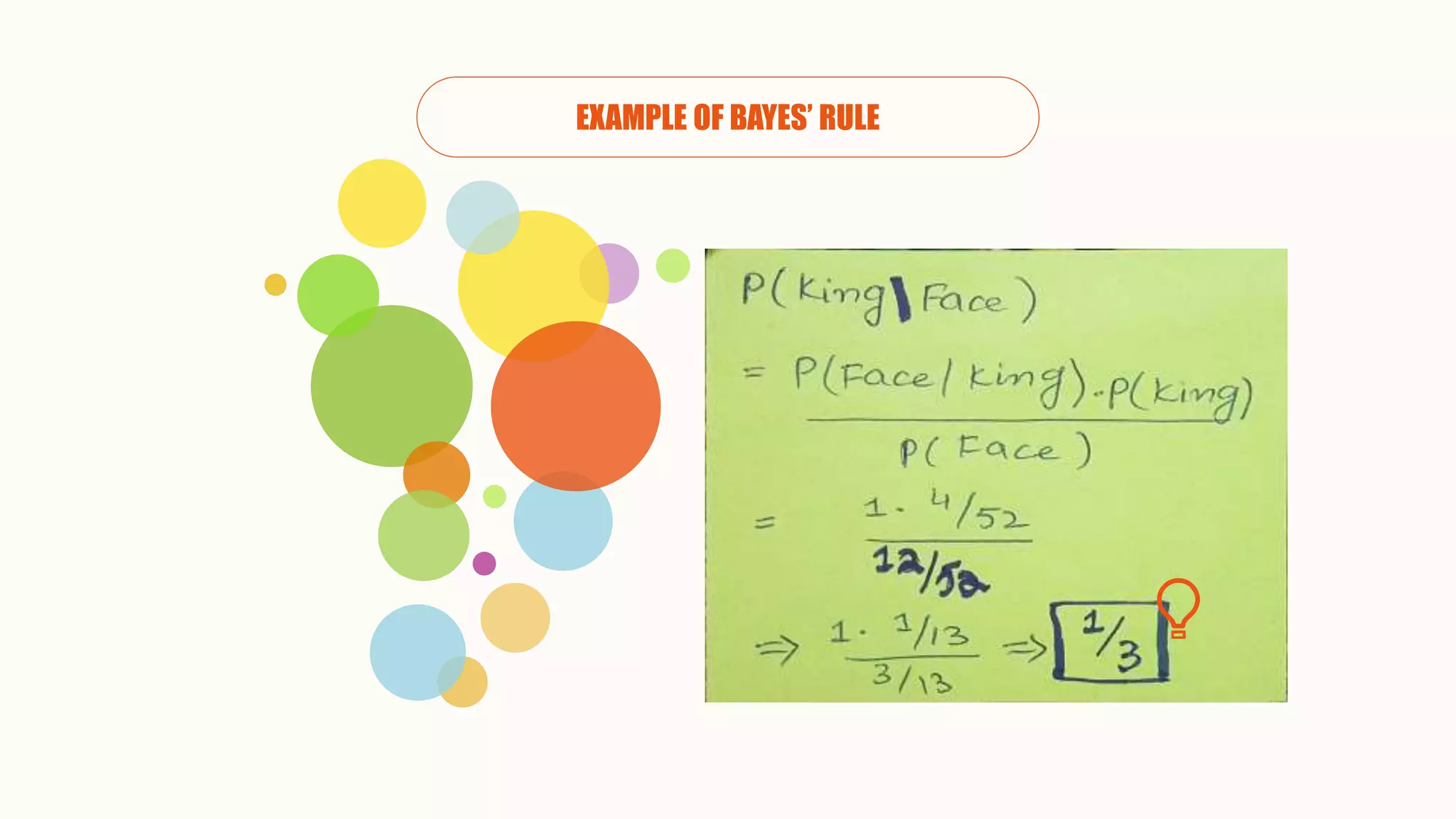
The document discusses uncertainty and probabilistic reasoning. It begins by defining uncertainty as situations where the truth or falsity of predicates is unknown. This requires probabilistic reasoning to represent uncertain knowledge. Probabilistic reasoning is necessary for domains where complete and consistent models cannot be created, like the real world which contains true uncertainty. Bayes' rule is then introduced as a mathematical formula for determining conditional probabilities of events given prior knowledge. Examples are provided to demonstrate calculating conditional probabilities. The document contrasts rule-based systems with machine learning approaches for probabilistic reasoning.

1. GROUP 7
1922110028
1922110046
1922110043
1922110025
1922110048
1922110032
Reporter: Time:

2. contents
01 UNCERTAINITY
CAUSE OF UNCERTENTAINTY
02
03
PROBABILITY REASONING
NEED OF PROBABLITY
REASONING
04 CONDITIONAL PROBABILITY
05 RULE BASED IN AI AND
MACHINE LEARNING
RULES OF PROBABILITY
REASONING
06 REASONING TYPES

3. 01
 UNCERTAINITY
 CAUSES OF UNCERTAINITY

4. Uncertainty:
• Till now, we have learned knowledge representation using
first-order logic and propositional logic with certainty, which
means we were sure about the predicates. With this
knowledge representation, we might write A→B, which means
if A is true then B is true, but consider a situation where we
are not sure about whether A is true or not then we cannot
express this statement, this situation is called uncertainty.
• So to represent uncertain knowledge, where we are not sure
about the predicates, we need uncertain reasoning or
probabilistic reasoning.

5. 03
Equipment fault
.
04
Temperature variation
01
02
Information occurred from unreliable
sources.
.
Experimental Errors
YOUR TITLE
01 YOUR TITLE
05
Climate change.
CAUSES OF UNCERTAINITY

6. 02
 PROBABILITY REASONING

7. Probability reasoning
In many problem domains it is not possible to
create complete, consistent models of the
world.Therefore agents and people must act in
uncertain worlds (which the real world is).

8. Reasons for reasoning probability
• TRUE UNCERTAINITY:flipping a coin.
• THEORATICAL IGNORANCE:There is no complete
theory which is known about the problem E.g. some
peculiar ( ‫)عجیب‬medical diagnosis.
• LAZINESS:The space of relevant factors is very
large,and would require too much work to list the
complete set of antecedents(‫)سابقہ‬.
• Logic deals with certainities while probability deals
with uncertainities.

9. 03
 BAYES’RULE

10. BAYES’ RULE
The Bayes’ theorem (also known as
the Bayes’ rule) is a mathematical
formula used to determine the
conditional probability of events.
Essentially, the Bayes’ theorem
describes the probability of an event
based on prior knowledge of the
conditions that might be relevant to the
event.
03 YOUR TITLE
BAYES RULE

11. 03 YOUR TITLE
PROVE BAYES’ RULE

12. 01
P(A|B) – the probability of
event A occurring, given
event B has occurred.
02
P(B|A) – the probability of
event B occurring, given
event A has occurred
04
P(B) – the probability of
event B
03
P(A) – the probability of
event A
03 YOUR TITLE

13. EXAMPLE OF BAYES’ RULE

14. 04
 PROBABILITY

15. Probability:-
• Probability can be defined as a chance that an uncertain event
will occur. It is the numerical measure of the likelihood that an
event will occur. The value of probability always remains
between 0 and 1 that represent ideal uncertainties.
• 0 ≤ P(A) ≤ 1, where P(A) is the probability of an event A.
• P(A) = 0, indicates total uncertainty in an event A.
• P(A) =1, indicates total certainty in an event A.
•

16. • Event: Each possible outcome of a variable is called an event.
• Sample space: The collection of all possible events is called sample space.
• Conditional probability:-
• Conditional probability is a probability of occurring an event when another
event has already happened.
• Where P(A⋀B)= Joint probability of a and B
• P(B)= Marginal probability of B.

17. Example:
• In a class, there are 70% of the students who like English and 40% of the
students who likes English and mathematics, and then what is the percent
of students those who like English also like mathematics?
Solution:
• Let, A is an event that a student likes Mathematics
• B is an event that a student likes English.
• Hence, 57% are the students who like English also like Mathematics.

18. 05
 RULE BASED AND MACHINE LEARNING

19. RULE BASED & MACHINE LEARNING
ALGORITHIM

20. 06
 FARWORD PROBABILITY
 BACKWARD PROBABILITY

23. THANK YOU!
T H A N K Y O U F O R W A T C H I N G