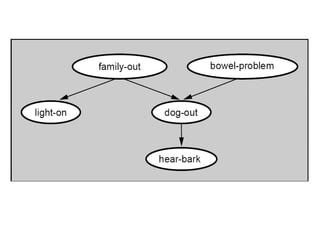
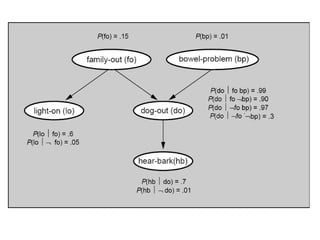
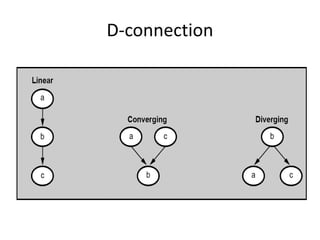
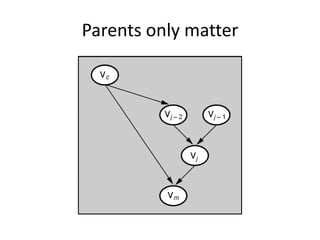
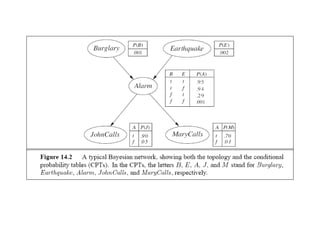
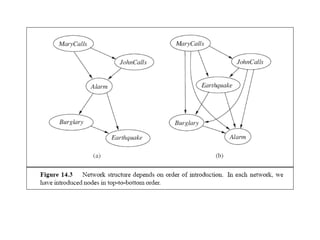
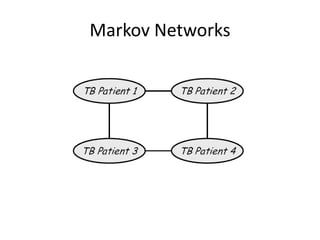
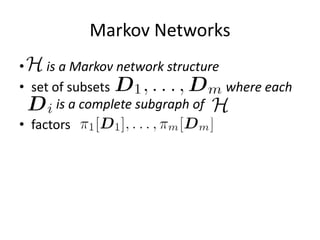
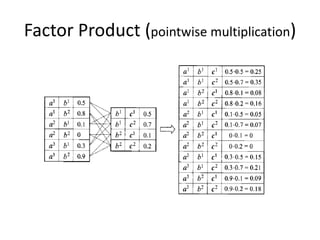
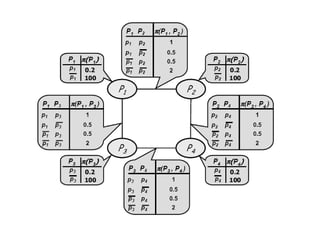
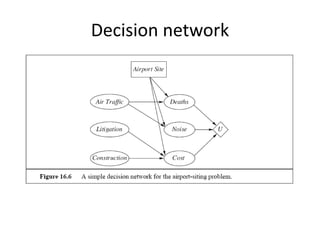
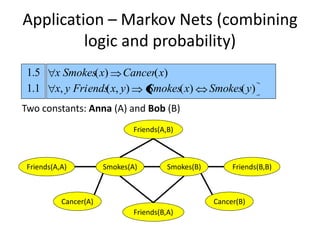
Graphical models provide a framework for combining probabilities and logical structures to compactly represent complex phenomena. Bayesian networks are a type of graphical model that use directed graphs to represent conditional independence relationships between variables. Each node corresponds to a variable with a conditional probability distribution. This factorization allows compressing a full joint distribution into a smaller set of local distributions. Markov networks are another type of graphical model that use undirected graphs and factors to represent relationships without directionality. Graphical models have applications in areas like medical diagnosis, computer vision, and combining logic and probability. Tools exist to help construct and evaluate graphical models.

1. Graphical Models
for dummies
Max Khesin, Data Strategist,
Liquidnet Inc.

2. Graphical Models For
By Dummies

3. Grand Theme
• “Probabilistic graphical models are an elegant
framework which combines uncertainty
(probabilities) and logical structure
(independence constraints) to
compactlyrepresent complex, real-world
phenomena”. (Koller 2007)

4. Trying to guess if family is home.
• When wife leaves the house she leaves the outdoor
light on (but sometimes leaves it on for a guest)
• When wife leaves the house, she usually puts the
dog out
• When dog has a bowel problem, she goes to the
backyard
• If the dog is in the backyard, I will probably hear it
(but it might be the neighbor's dog)

6. These causal connections are not
absolute
Three causes of uncertainty (Norvig, Russell
2009):
- Laziness
- Theoretical Ignorance
- Practical Ignorance

7. Problem with probability
• Too many parameters
• For binary random variables, 2^n-1

8. Bayesean Network - definition
• A Bayesian network is a directed graph in which each
node is annotated with quantitative probability
information. The full specification is as follows:
1. Each node corresponds to a random variable, which
may be discrete or continuous.
2. A set of directed links or arrows connects pairs of
nodes. If there is an arrow from node X to node Y , X is
said to be a parent of Y. The graph has no directed
cycles (and hence is a directed acyclic graph, or DAG.
3. Each node Xi has a conditional probability distribution
P(Xi | Parents(Xi)) that quantifies the effect of the
parents on the node. (Russell, Norvig 2009)

10. Compressed distribution (factorization)
• In our Bayesian system, we only have 10
parameters
• The compression is due to independence
• Independence is how causality manifests itself
in the distribution

11. D-connection

12. Definition: conditional probability

13. Decomposing a joint distribution
…

14. Topologic sort:
• “topological ordering of a directed acyclic
graph (DAG) is a linear ordering of its nodes in
which each node comes before all nodes to
which it has outbound edges” - Wikipedia.

15. Sorting the family-home example
• Family-out(1), Bowel-problem(2), Ligths-
On(3), Dog-out(4), Hear-bark(4)
• Bowel-problem(1), Family-out(2), Ligths-
On(3), Dog-out(4), Hear-bark(5)
• Right away, we got all the non-descendants to
the left of the variable

16. Parents only matter

17. Chain rule for Bayesian Networks

20. Markov Networks
• These models are useful in modeling a variety
of phenomena where one cannot naturally
ascribe a directionality to the interaction
between variables

21. Markov Networks

22. Markov Networks
• D is a set of random variables
• Factor to be a function from Val(D) to IR+.

23. Markov Networks
• H is a Markov network structure
• set of subsets D1, . . . ,Dm, where each
Di is a complete subgraph of H
• factors

24. Markov Network - factorization
Where the unnormalized measure is
And normalization factor is

25. Factor Product (pointwise multiplication)

27. Decision Networks
- Combine Bayesian Networks with Utility
Theory

28. Utility-based agent

29. Decision network

30. Evaluating decision network

31. Applications – Bayes Nets
• Expert systems.
• “…A later evaluation showed that the diagnostic accuracy of
Pathfinder IV was at least as good as that of the expert used
to design the system. When used with less expert pathologists,
the system significantly improved the diagnostic accuracy of
the physicians alone. Moreover, the system showed greater
ability to identify important findings and to integrate these
findings into a correct diagnosis. Unfortunately, multiple
reasons prevent the widespread adoption of Bayesian
networks as anaid for medical diagnosis, including legal
liability issues for misdiagnoses and incompatibility with the
physicians' workflow” (Koller 2009)

32. Applications – Markov Networks
• Computer vision – segmentation
• Regions are contiguous. Glove is next to the
arm
“superpixels”

33. Application – Markov Nets (combining
logic and probability)
1.5 x Smokes( x) Cancer( x)
1.1 x, y Friends x, y)
( Smokes( x) Smokes( y)
Two constants: Anna (A) and Bob (B)
Friends(A,B)
Friends(A,A) Smokes(A) Smokes(B) Friends(B,B)
Cancer(A) Cancer(B)
Friends(B,A)

34. Road to AGI…

35. Tools
• Netica - http://www.norsys.com/netica.html
• Really, look here
http://www.cs.ubc.ca/~murphyk/Bayes/bnsof
t.html

36. References
• Russell, Norvig 2009: Artificial Intelligence: A Modern Approach (AIMA)
http://aima.cs.berkeley.edu/ (amazon)
• Getoor, Taskar 2007: Introduction to Statistical Relational Learning
http://www.cs.umd.edu/srl-book/ (amazon)
• Koller, Friedman 2009: Probabilistic Graphical Models: Principles and Techniques
http://pgm.stanford.edu/ (amazon)
• Charniak 1991: Bayesian Networks without Tears.
www.cs.ubc.ca/~murphyk/Bayes/Charniak_91.pdf
• CS228: http://www.stanford.edu/class/cs228/ (course available via SCPD)
• Domingos, practical statistical learning in AI
http://www.cs.cmu.edu/~tom/10601_sp08/slides/mlns-april-28.ppt, see also
http://www.youtube.com/watch?v=bW5DzNZgGxY
• Koller 2007: “Graphical Models in a Nutshell”, a chapter of Getoor, Taskar 2007,
availavle online http://www.seas.upenn.edu/~taskar/pubs/gms-srl07.pdf