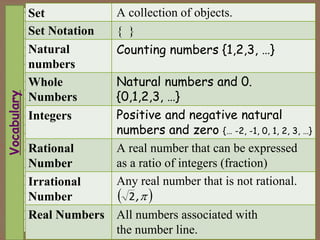
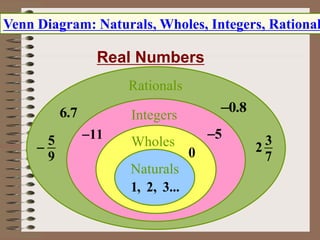
The document is a presentation focused on the operations of rational numbers, aimed at helping students apply the order of operations and their properties to solve problems. It defines key concepts including rational and irrational numbers, as well as their representations on the number line and in set notation. Additionally, it poses essential questions to guide students' understanding of these mathematical concepts.

1. PRESENTATION ON OPERATIONS OF
RATIONAL NUMBER
Presented By : Ms. Nidhi Mahajan

2. Student Objective:
• Students will apply order of operations to
solve problems with rational numbers and
apply their properties, by performing the
correct operations, using math facts
skills, writing reflective summaries, and
scoring 80% proficiency

3. Set
Set Notation
Natural
numbers
Whole
Numbers
Rational
Number
Integers
Irrational
Number
Real Numbers All numbers associated with
the number line.
Vocabulary

4. Set A collection of objects.
Set Notation { }
Natural
numbers
Counting numbers {1,2,3, …}
Whole
Numbers
Natural numbers and 0.
{0,1,2,3, …}
Rational
Number
Integers Positive and negative natural
numbers and zero {… -2, -1, 0, 1, 2, 3, …}
A real number that can be expressed
as a ratio of integers (fraction)
Irrational
Number
Any real number that is not rational.
Real Numbers All numbers associated with
the number line.
 

,
2
Vocabulary

5. Essential Questions:
• How do you know if a number is a
rational number?
• What are the properties used to
evaluate rational numbers?

6. Two Kinds of Real Numbers
• Rational Numbers
• Irrational Numbers

7. Rational Numbers
• A rational number is
a real number that
can be written as a
ratio of two
integers.
• A rational number
written in decimal
form is terminating
or repeating.
EXAMPLES OF
RATIONAL NUMBERS
16
1/2
3.56
-8
1.3333…
-3/4

8. Irrational Numbers
• An irrational
number is a
number that
cannot be written
as a ratio of two
integers.
• Irrational numbers
written as
decimals are non-
terminating and
non-repeating.
• Square roots of
non-perfect
“squares”
• Pi- īī
17

9. Venn Diagram: Naturals, Wholes, Integers, Rational
Naturals
1, 2, 3...
Wholes
0
Integers
11
 5

Rationals
6.7
5
9

0.8

3
2
7
Real Numbers

10. Whole numbers and their opposites.
Natural Numbers - Natural counting numbers.
1, 2, 3, 4 …
Whole Numbers - Natural counting numbers and zero.
0, 1, 2, 3 …
Integers -
… -3, -2, -1, 0, 1, 2, 3 …
Integers, fractions, and decimals.
Rational Numbers -
Ex: -0.76, -6/13, 0.08, 2/3
Rational Numbers