Download to read offline
Uploaded byFan Zhitao
EM 3D reconstruction
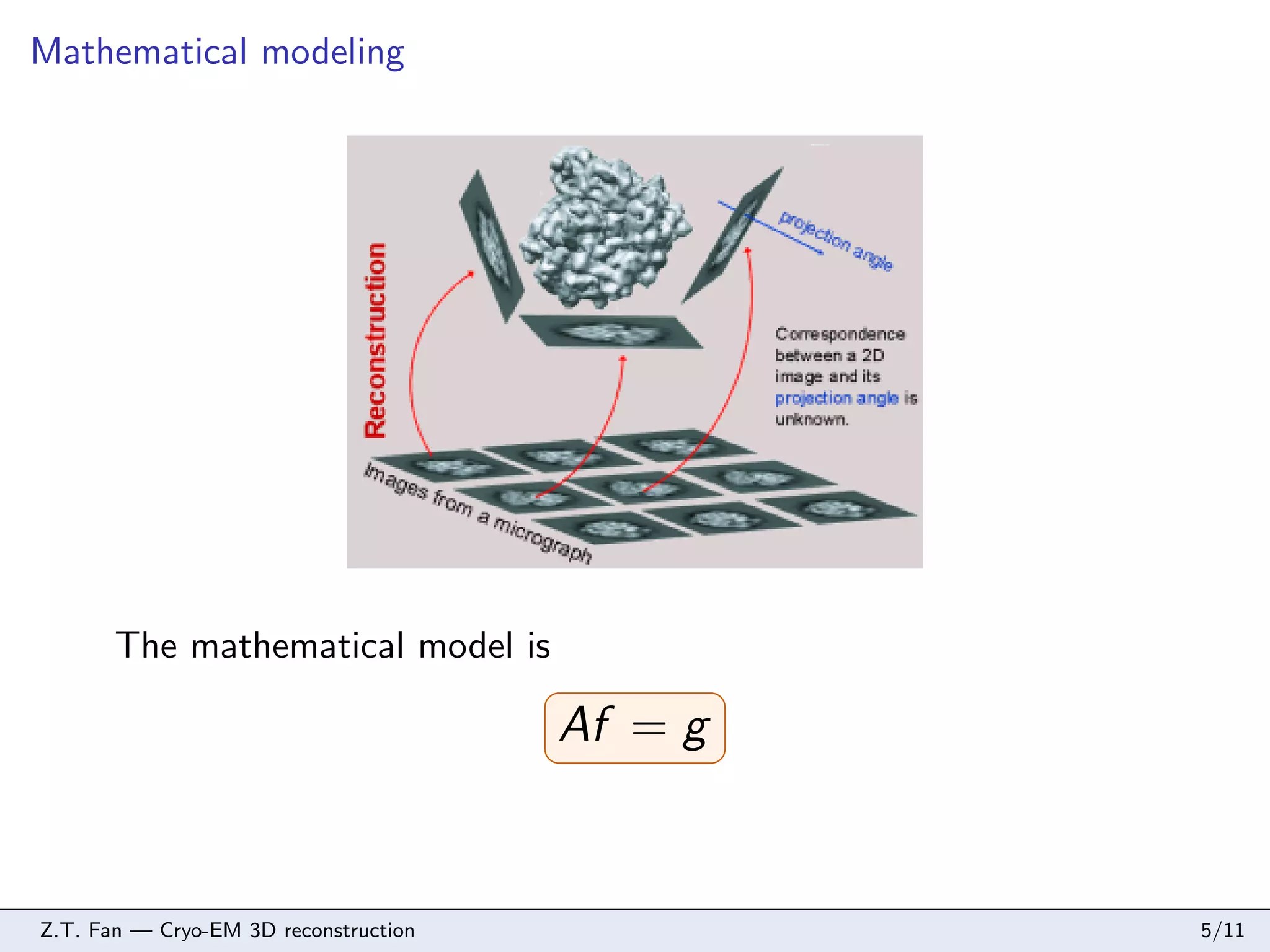
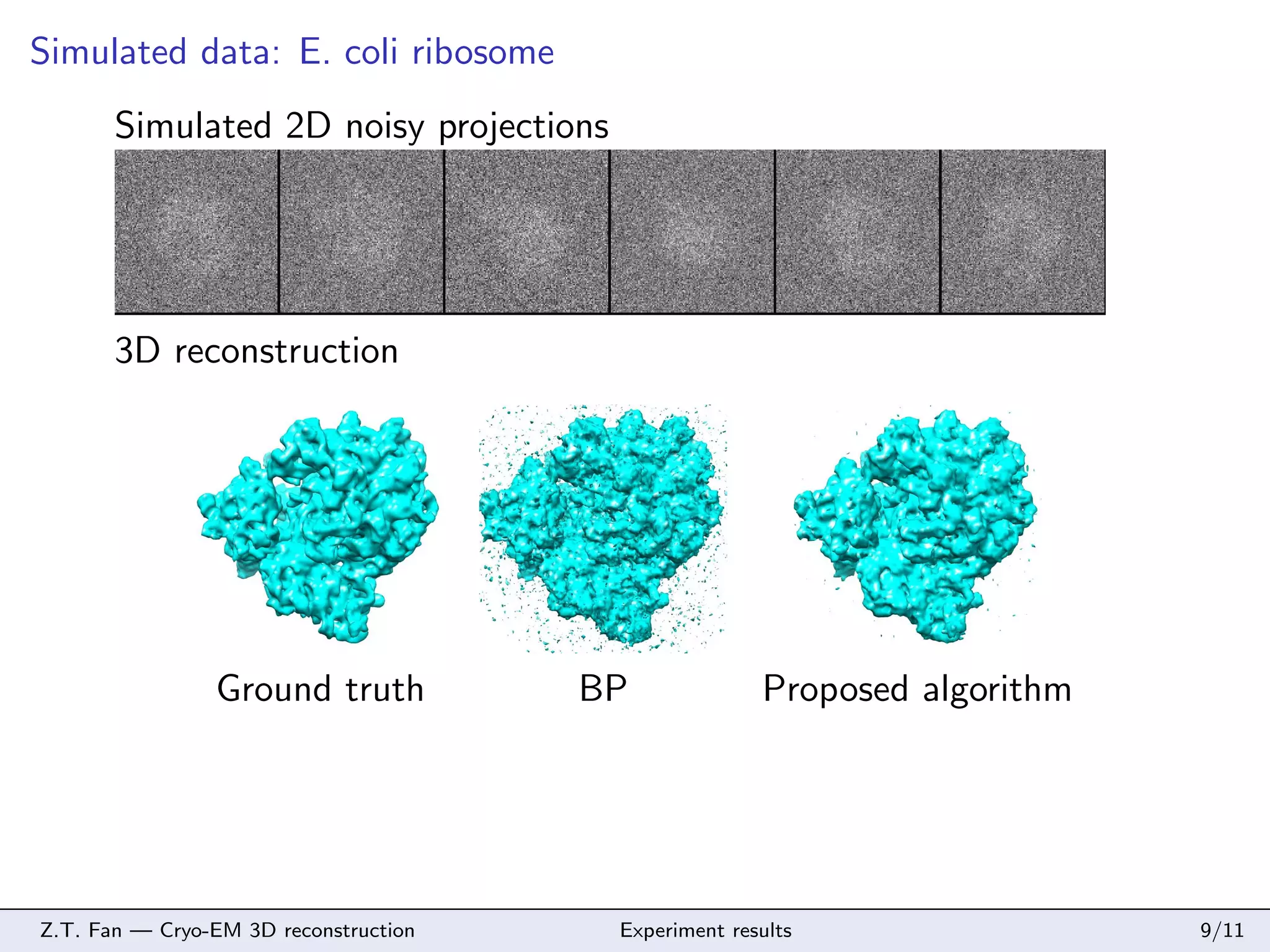
This document discusses cryo-electron microscopy (cryo-EM) 3D reconstruction techniques. It describes the cryo-EM imaging process and challenges in reconstructing 3D structures from 2D projection images, including large noise and data size. The document proposes a memory-saving algorithm using tight wavelet frames for cryo-EM 3D reconstruction that formulates the reconstruction as a sparse representation problem solved with soft-thresholding and gradient descent. Simulation results on an E. coli ribosome and experimental results on an adenovirus demonstrate the proposed algorithm can reconstruct 3D structures from noisy projection data.
EM 3D reconstruction
- 1. Cryo-EM 3D reconstruction FanZhitao NUS Graduate School February 20, 2014
- 2. Images are everywhere Inour life In research Z.T. Fan — Cryo-EM 3D reconstruction 2/11
- 3. EM imaging process Z.T.Fan — Cryo-EM 3D reconstruction 3/11
- 4. The EM images Z.T.Fan — Cryo-EM 3D reconstruction 4/11
- 5. Mathematical modeling The mathematicalmodel is Af = g Z.T. Fan — Cryo-EM 3D reconstruction 5/11
- 6. Challenges Challenges: large noise large data:100, 000 projections with size 512 A is hard to write out Contribution Proposed a memory-saving tight wavelet frame based algorithm Done the convergence analysis of this algorithm Z.T. Fan — Cryo-EM 3D reconstruction 6/11
- 7. Sparse representation The imagehas a sparse representation under wavelet system. If we have a sparse representation, we may formulate a mathematical model: min g − Af f 2 + λ Wf 1 W is the discrete wavelet transform. Dong and Shen 2005, Ron and Shen 1995 Z.T. Fan — Cryo-EM 3D reconstruction 7/11
- 8. The algorithm Algorithm 1 fk+1= (I − µA A)W Tλ Wfk + µA g The advantage Simple: one soft-thresholding and one gradient descent Small memory footprint: one wavelet transform Z.T. Fan — Cryo-EM 3D reconstruction 8/11
- 9. Simulated data: E.coli ribosome Simulated 2D noisy projections 3D reconstruction Ground truth Z.T. Fan — Cryo-EM 3D reconstruction BP Proposed algorithm Experiment results 9/11
- 10. Real data: Adenovirus 2Dnoisy projections 3D reconstruction BP Z.T. Fan — Cryo-EM 3D reconstruction Proposed algorithm Experiment results 10/11
- 11. Thank you! Special thanksto DR Li Ming, Chinese Academy of Science Prof Ji Hui, NUS mathematics Prof Shen Zuowei, NUS mathematics Z.T. Fan — Cryo-EM 3D reconstruction Acknowledgement 11/11