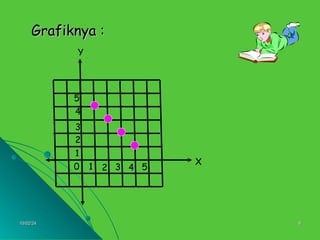
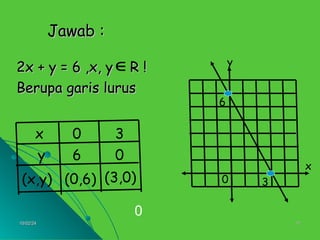
Dokumen ini membahas materi sistem persamaan linear dua variabel (SPLDV) untuk kelas VIII, termasuk perbedaan dengan persamaan linear satu variabel dan memberikan contoh bentuk umum SPLDV. Terdapat penjelasan tentang grafik himpunan penyelesaian dari persamaan, baik untuk variabel bilangan real maupun bilangan lainnya. Contoh-contoh konkret disajikan untuk memudahkan pemahaman siswa terkait topik ini.

1. 10/02/24
1

2. 10/02/24
2
MATEMATIKA
KELAS VIII
 SEMESTER SATU/GANJIL
 MATERI DAN LATIHAN
BAB IV
SISTEM PERSAMAAN LINEAR
DUA VARIABEL

3. 10/02/24
10/02/24 3
3
A. BENTUK-BENTUK SPLDV
1. Perbedaan PLDV dan SPLDV
a. Persamaan linear dengan satu
variabel (PLSV) .
Persamaan linear dengan satu
variabel adalah persamaan yang
memiliki satu variabel dan pangkat
masing-masing variabel sama dengan
satu .

4. 10/02/24
10/02/24 4
4
Contoh :
Contoh :
5 = x – 3
5 = x – 3
3a + 2 = 10
3a + 2 = 10
3m = 2m – 1
3m = 2m – 1
Dimana x , a , dan m merupakan
Dimana x , a , dan m merupakan
variabel.
variabel.

5. 10/02/24
10/02/24 5
5
b. Persamaan Linear Dua Variabel
b. Persamaan Linear Dua Variabel
Persamaan Linear Dua Variabel adalah
Persamaan Linear Dua Variabel adalah
persamaan yang memiliki dua variabel
persamaan yang memiliki dua variabel
dan masing-masing variabel sama
dan masing-masing variabel sama
dengan satu .
dengan satu .
Bentuk umum :
Bentuk umum :
ax + by = c , a, b tidak sama dengan 0
ax + by = c , a, b tidak sama dengan 0
x dan y sebagai variabel .
x dan y sebagai variabel .

6. 10/02/24
10/02/24 6
6
Contoh :
Contoh :
1. x + y = 3
1. x + y = 3
2. x – 3y = 6
2. x – 3y = 6
3. 5y – 3x = 8
3. 5y – 3x = 8
Dimana x dan y merupakan variabel
Dimana x dan y merupakan variabel

7. 10/02/24
10/02/24 7
7
c. Grafik Himpunan Penyelesaian
c. Grafik Himpunan Penyelesaian
Adapun Grafik Himpunan Penyelesaian
Adapun Grafik Himpunan Penyelesaian
dari suatu persamaan linear dua variabel
dari suatu persamaan linear dua variabel
untuk variabel pada himpunan bilangan
untuk variabel pada himpunan bilangan
selain bilangan real berupa noktah-
selain bilangan real berupa noktah-
noktah .
noktah .
Contoh :
Contoh :
Tentukan himpunan penyelesaian dari
Tentukan himpunan penyelesaian dari
x + y = 5 , x A !
x + y = 5 , x A !


8. 10/02/24
10/02/24 8
8
Jawab :
Jawab :
x + y = 5 , x , y A
x + y = 5 , x , y A
Himpunan penyelesaiannya merupakan titik
Himpunan penyelesaiannya merupakan titik
(x,y) yang memenuhi x + y = 5 , yaitu :
(x,y) yang memenuhi x + y = 5 , yaitu :
Untuk x = 1 , maka y = 4 titiknya (1,4)
Untuk x = 1 , maka y = 4 titiknya (1,4)
Untuk x = 2 , maka y = 3 titiknya (2,3)
Untuk x = 2 , maka y = 3 titiknya (2,3)
Untuk x = 3 , maka y = 2 titiknya (3,2)
Untuk x = 3 , maka y = 2 titiknya (3,2)
Untuk x = 4 , maka y = 1 titiknya (4,1)
Untuk x = 4 , maka y = 1 titiknya (4,1)
Untuk x = 5 , maka y = 0 titiknya (5,0)
Untuk x = 5 , maka y = 0 titiknya (5,0)
Hp = { (1,4),(2,3),(3,2),(4,1),(5,0) }
Hp = { (1,4),(2,3),(3,2),(4,1),(5,0) }


9. 10/02/24
10/02/24 9
9
Grafiknya :
Grafiknya :
Y
1
0
1
2
3
4
2 3 4 5
5
X

10. 10/02/24
10/02/24 10
10
Adapun Grafik Himpunan Penyelesaian
Adapun Grafik Himpunan Penyelesaian
dari suatu persamaan linear dua variabel
dari suatu persamaan linear dua variabel
untuk variabel pada himpunan bilangan
untuk variabel pada himpunan bilangan
real ( R ) berupa garis lurus .
real ( R ) berupa garis lurus .
Contoh :
Contoh :
Gambarlah grafik dari 2x + y = 6 ,x, y R !
Gambarlah grafik dari 2x + y = 6 ,x, y R !


11. 10/02/24
10/02/24 11
11
Jawab :
Jawab :
2x + y = 6 ,x, y R !
2x + y = 6 ,x, y R !
Berupa garis lurus
Berupa garis lurus

y
x
(x,y)
0
6
3
0
(0,6) (3,0)
0
6
0 3
x
y

12. 10/02/24
10/02/24 12
12