Recommended
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PPTX
PPTX
PDF
PDF
PDF
[Dl輪読会]introduction of reinforcement learning
More Related Content Viewers also liked
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PPTX
PPTX
PDF
Similar to Ppt godo g
PDF
PDF
[Dl輪読会]introduction of reinforcement learning
PDF
PPTX
[DL輪読会]Learn What Not to Learn: Action Elimination with Deep Reinforcement Le...
PDF
20150319 jmrx 50th_behavioural_economics_v2_kokai
PDF
PDF
PPT
130425 discrete choiceseminar_no.2
PDF
Ml professional bandit_chapter1
PPTX
PDF
異常行動検出入門 – 行動データ時系列のデータマイニング –
PDF
PPTX
PPTX
【輪読会】Braxlines: Fast and Interactive Toolkit for RL-driven Behavior Engineeri...
PDF
PPTX
強化学習エージェントの内発的動機付けによる探索とその応用(第4回 統計・機械学習若手シンポジウム 招待公演)
PDF
強化学習勉強会・論文紹介(第50回)Optimal Asset Allocation using Adaptive Dynamic Programming...
PDF
PDF
PPTX
強化学習の基礎と深層強化学習(東京大学 松尾研究室 深層強化学習サマースクール講義資料)
More from harmonylab
PDF
Collaborative Document Simplification Using Multi-Agent Systems
PDF
Can Large Language Models perform Relation-based Argument Mining?
PDF
UniPAD: A Universal Pre-training Paradigm for Autonomous Driving
PDF
Efficient anomaly detection in tabular cybersecurity data using large languag...
PDF
APT-LLM Embedding-Based Anomaly Detection of Cyber Advanced Persistent Threat...
PDF
CTINexus: Automatic Cyber Threat Intelligence Knowledge Graph Construction Us...
PDF
Mixture-of-Personas Language Models for Population Simulation
PDF
QuASAR: A Question-Driven Structure-Aware Approach for Table-to-Text Generation
PDF
Large Language Model based Multi-Agents: A Survey of Progress and Challenges
PDF
Mixture-of-Personas Language Models for Population Simulation
PDF
TransitReID: Transit OD Data Collection with Occlusion-Resistant Dynamic Pass...
PDF
Data Scaling Laws for End-to-End Autonomous Driving
PDF
DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Lea...
PDF
Is Ego Status All You Need for Open-Loop End-to-End Autonomous Driving?
PDF
Encoding and Controlling Global Semantics for Long-form Video Question Answering
PDF
AECR: Automatic attack technique intelligence extraction based on fine-tuned ...
PDF
Enhancing Zero-Shot Chain-of-Thought Reasoning in Large Language Models throu...
PDF
Towards Scalable Human-aligned Benchmark for Text-guided Image Editing
PDF
Multiple Object Tracking as ID Prediction
PDF
【卒業論文】LLMを用いたMulti-Agent-Debateにおける反論の効果に関する研究
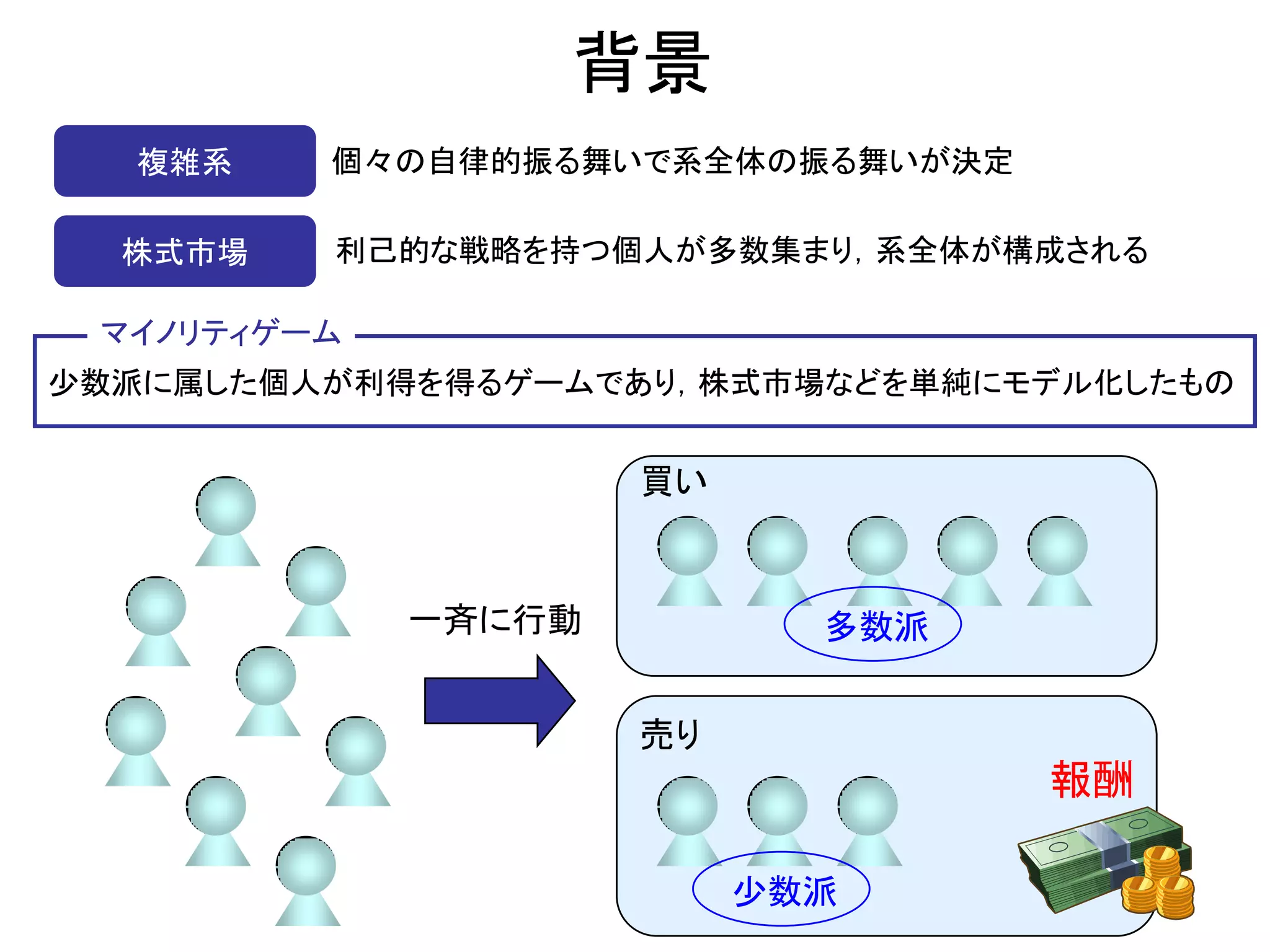
Ppt godo g 1. 2. 背景
複雑系 個々の自律的振る舞いで系全体の振る舞いが決定
株式市場 利己的な戦略を持つ個人が多数集まり,系全体が構成される
マイノリティゲーム
少数派に属した個人が利得を得るゲームであり,株式市場などを単純にモデル化したもの
買い
一斉に行動 多数派
売り
報酬
少数派
3. 目的
マイノリティゲームに関する先行研究
•StandardMGの研究(C-.Zhang 1997)
•人工市場のシンプルなモデルとしてのマイノリティゲーム
•進化的アルゴリズムは人工市場にふさわしいか[和泉 2004]
•エージェントの学習に「進化的アルゴリズム」を用いた研究
従来のMGではエージェントの行動はゲームの履歴だけで決定
現実にはうわさ,予想などの事前情報も考えて行動する
事前情報を含んだマイノリティゲームの提案
事前情報が行動に与える影響の分析
複雑系の側面をもつ株式市場をモデル化したマイノリティゲームを用いて,
事前情報が戦略の異なる複数の利己的エージェントの行動に与える影響を解析する
4. 行動決定テーブルを用いたマルチエージェントモデル
[和泉, et al., 04]
少数派だった行動
1 t-3 t-2 t-1 t
過去のゲームの履歴 A ・・・ B B A ?
各エージェントの行動でゲームをする
記憶長 m=2 の場合
報酬の獲得,行動決定テーブルの更新
t-2 t-1 t
報酬 行動決定テーブルの更新
A A P1
少数派 R 変更なし
A B P2 多数派 無し 確率α P3 ← P3
B A P3 確率1-α 変更なし
B B P4
行動決定テーブル 再びゲームをする
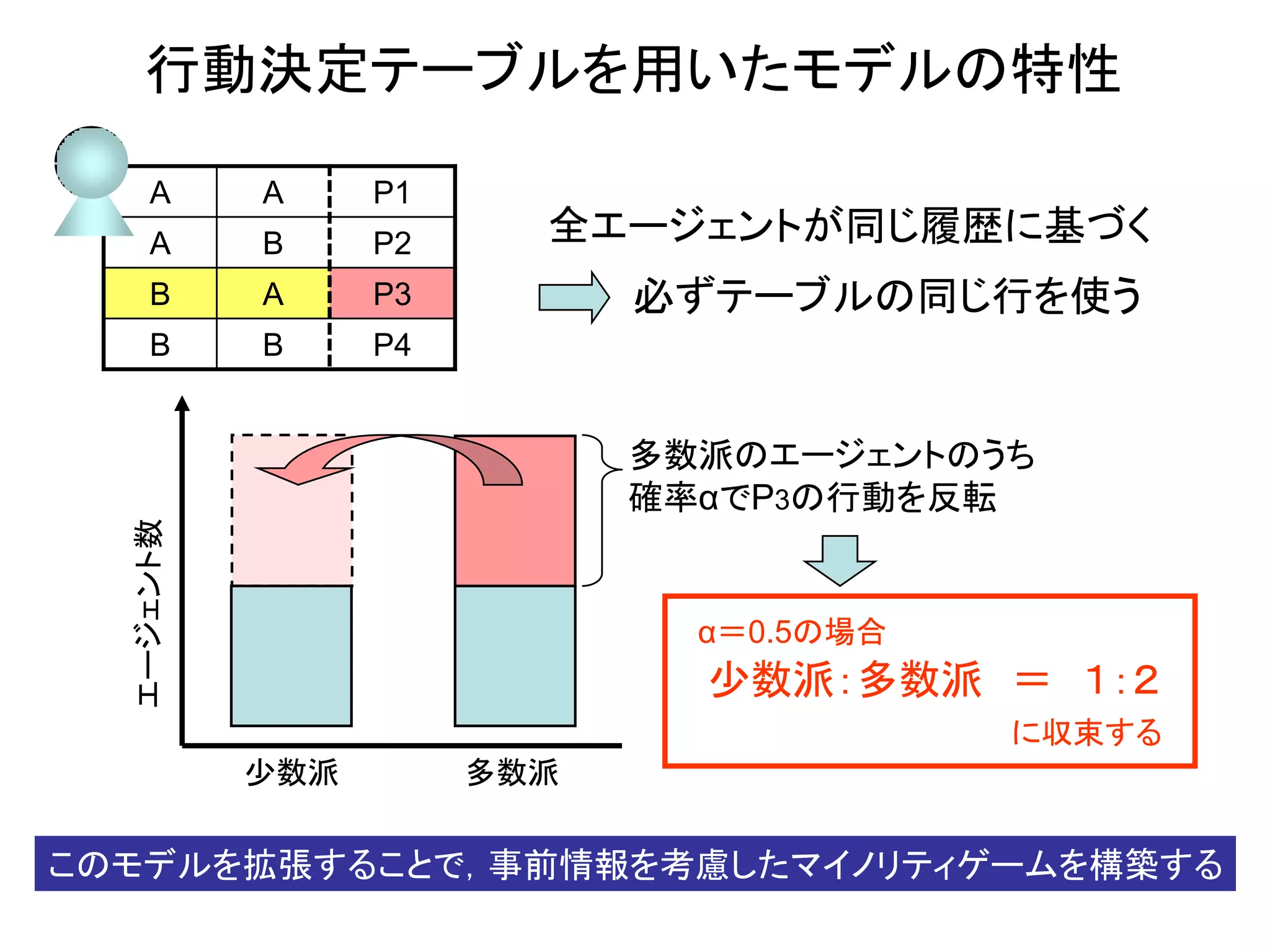
5. 行動決定テーブルを用いたモデルの特性
A A P1
A B P2 全エージェントが同じ履歴に基づく
B A P3 必ずテーブルの同じ行を使う
B B P4
多数派のエージェントのうち
確率αでP3の行動を反転
エージェント数
α=0.5の場合
少数派:多数派 = 1:2
に収束する
少数派 多数派
このモデルを拡張することで,事前情報を考慮したマイノリティゲームを構築する
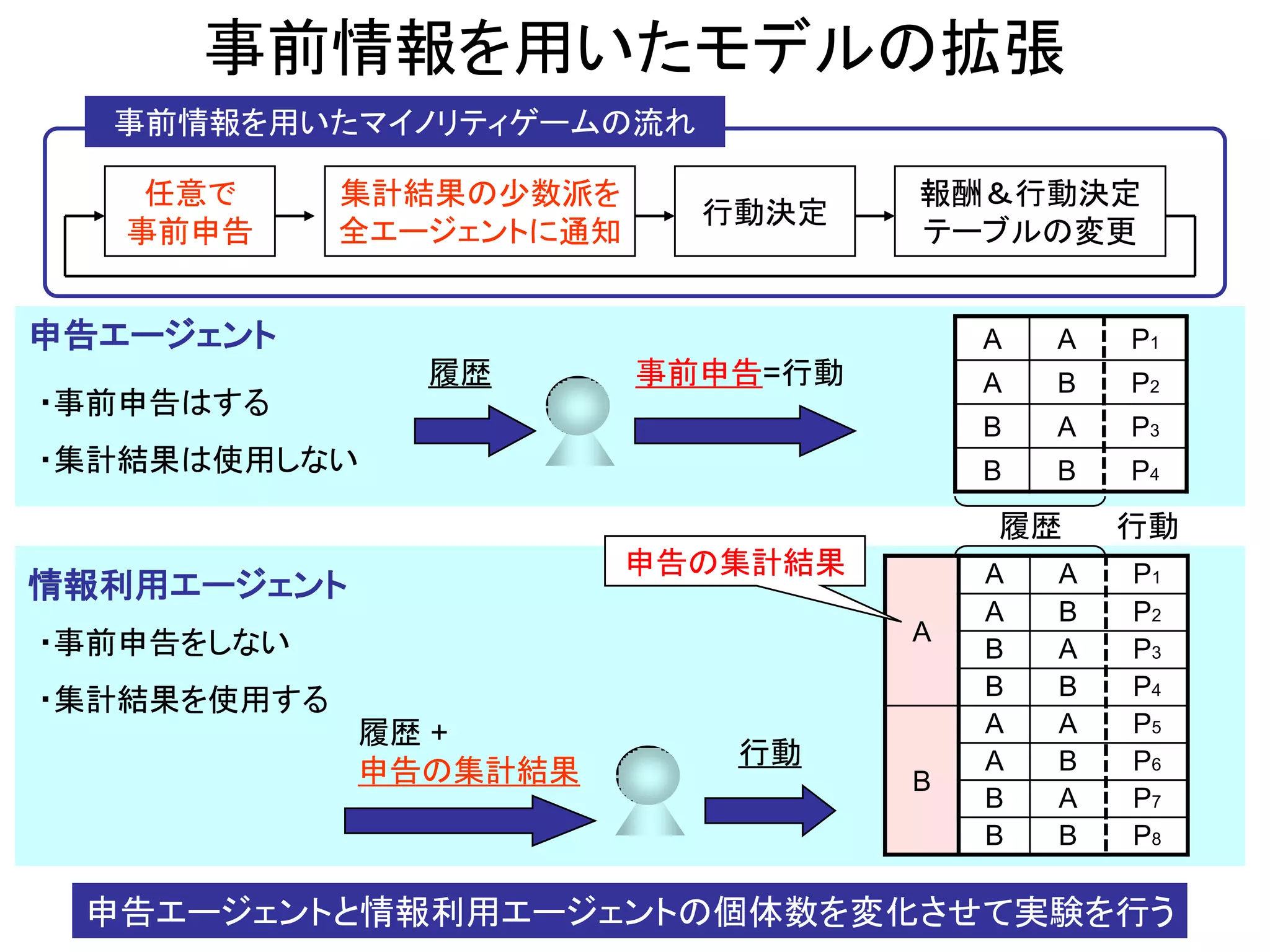
6. 事前情報を用いたモデルの拡張
事前情報を用いたマイノリティゲームの流れ
任意で 集計結果の少数派を 報酬&行動決定
行動決定
事前申告 全エージェントに通知 テーブルの変更
申告エージェント A A P1
履歴 事前申告=行動 A B P2
・事前申告はする
B A P3
・集計結果は使用しない B B P4
履歴 行動
申告の集計結果 A A P1
情報利用エージェント
A B P2
・事前申告をしない A
B A P3
B B P4
・集計結果を使用する
履歴 + A A P5
行動 A B P6
申告の集計結果 B
B A P7
B B P8
申告エージェントと情報利用エージェントの個体数を変化させて実験を行う
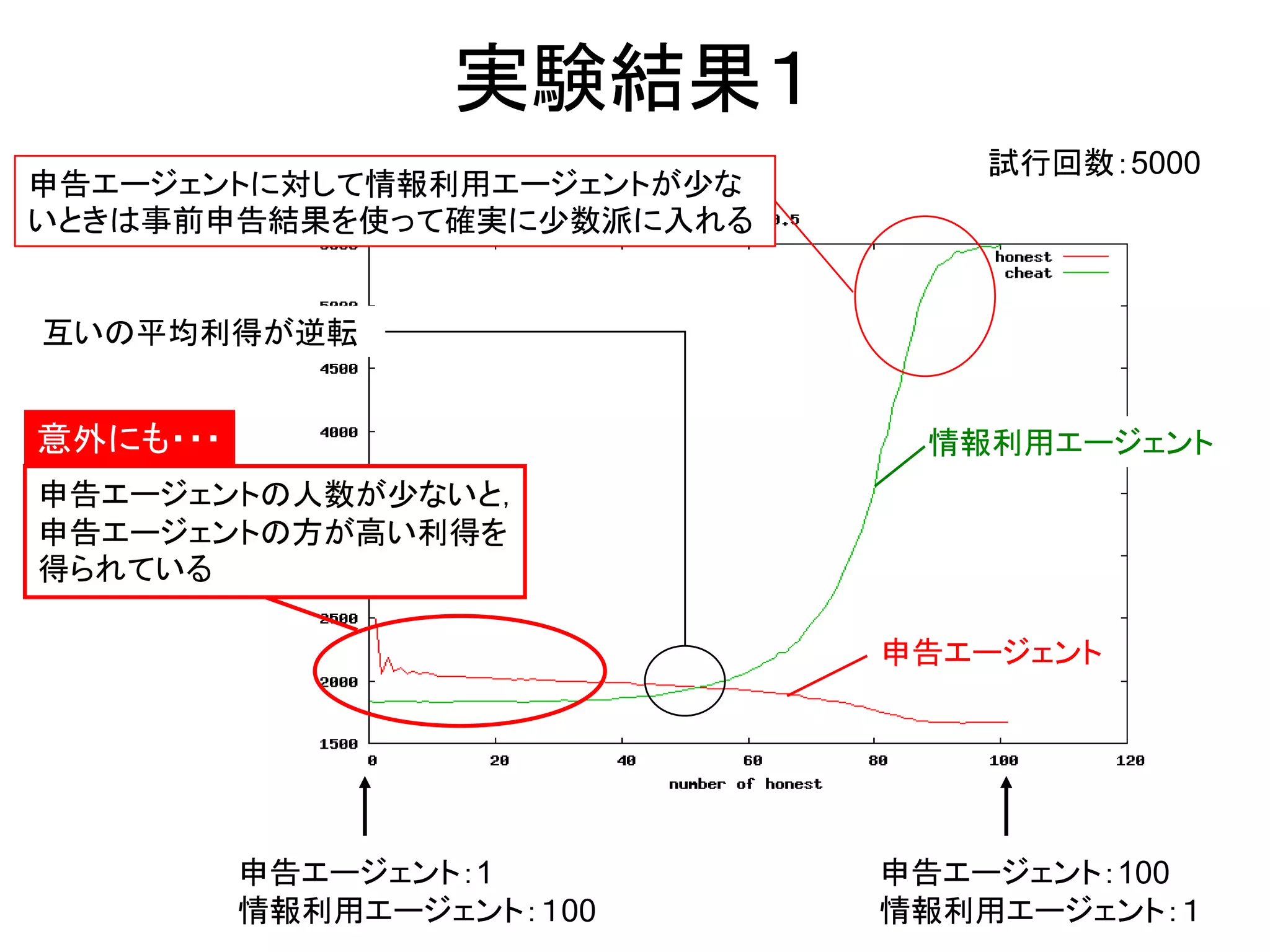
7. 実験結果1
試行回数:5000
申告エージェントに対して情報利用エージェントが少な
いときは事前申告結果を使って確実に少数派に入れる
互いの平均利得が逆転
意外にも・・・ 情報利用エージェント
申告エージェントの人数が少ないと,
申告エージェントの方が高い利得を
得られている
申告エージェント
申告エージェント:1 申告エージェント:100
情報利用エージェント:100 情報利用エージェント:1
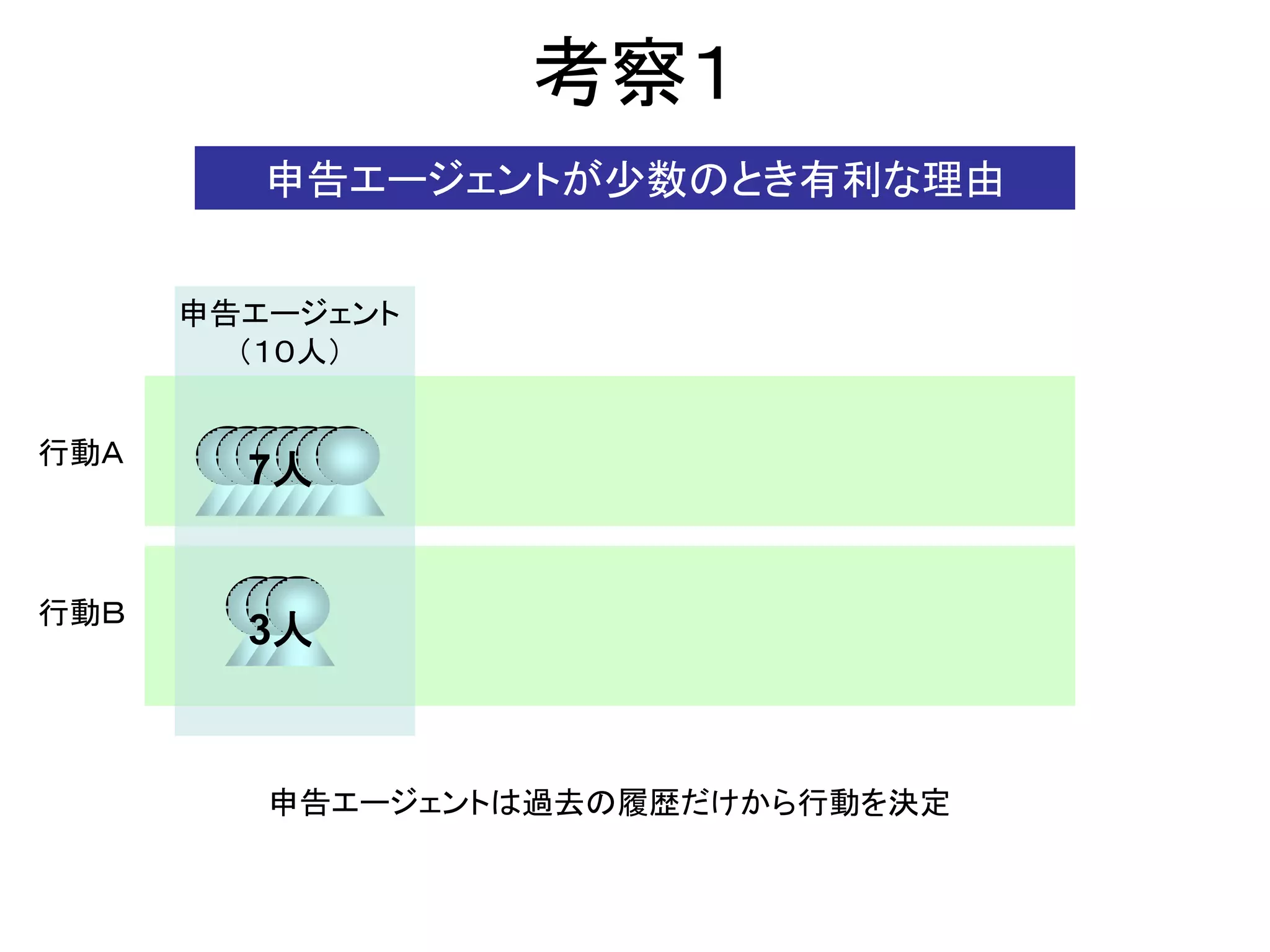
8. 考察1
申告エージェントが少数のとき有利な理由
申告エージェント
(10人)
行動A
7人
行動B
3人
申告エージェントは過去の履歴だけから行動を決定
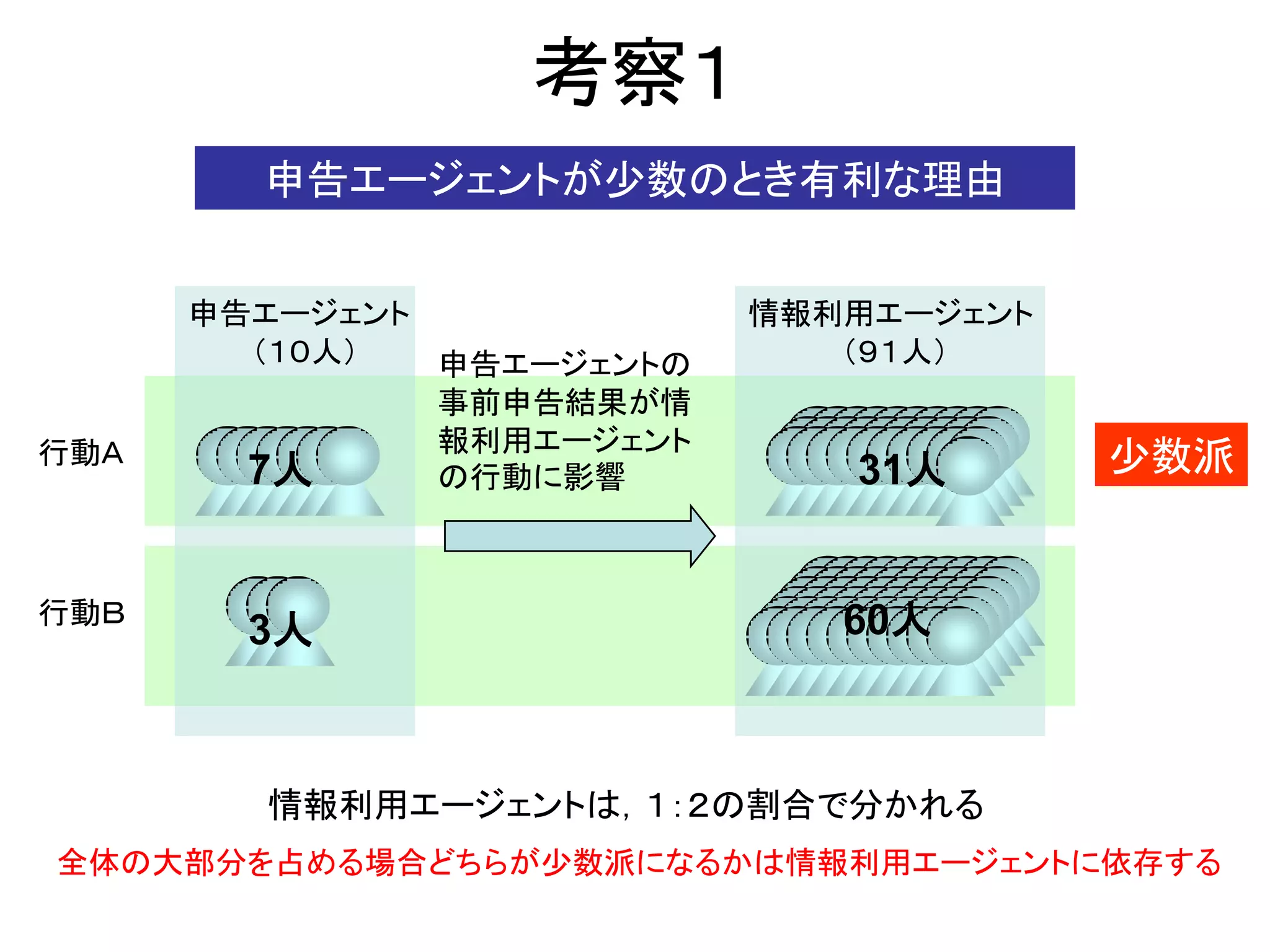
9. 考察1
申告エージェントが少数のとき有利な理由
申告エージェント 情報利用エージェント
(10人) 申告エージェントの (91人)
事前申告結果が情
報利用エージェント
行動A
7人 の行動に影響 31人 少数派
行動B 60人
3人
情報利用エージェントは,1:2の割合で分かれる
全体の大部分を占める場合どちらが少数派になるかは情報利用エージェントに依存する
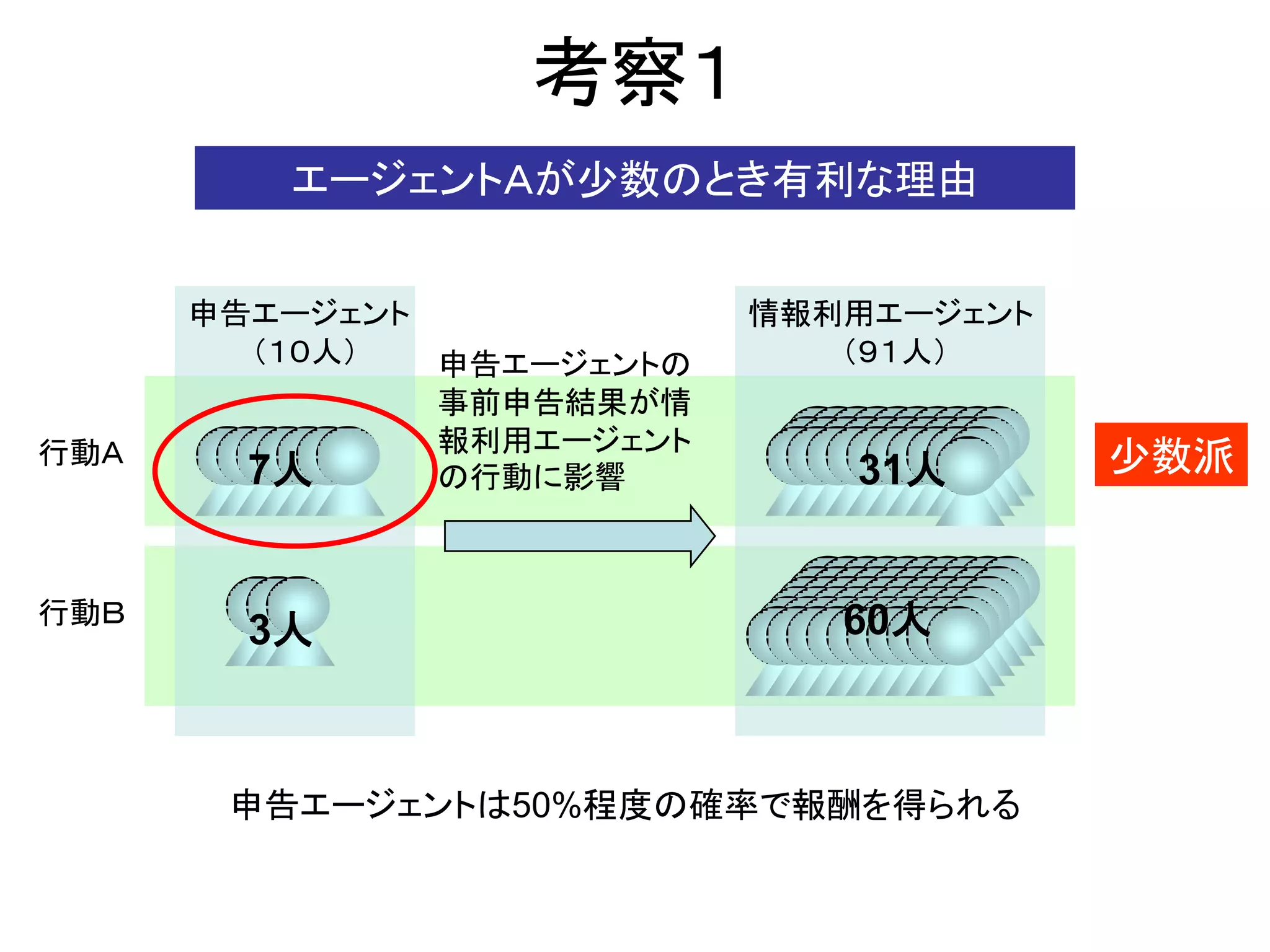
10. 考察1
エージェントAが少数のとき有利な理由
申告エージェント 情報利用エージェント
(10人) 申告エージェントの (91人)
事前申告結果が情
報利用エージェント
行動A
7人 の行動に影響 31人 少数派
行動B 60人
3人
申告エージェントは50%程度の確率で報酬を得られる
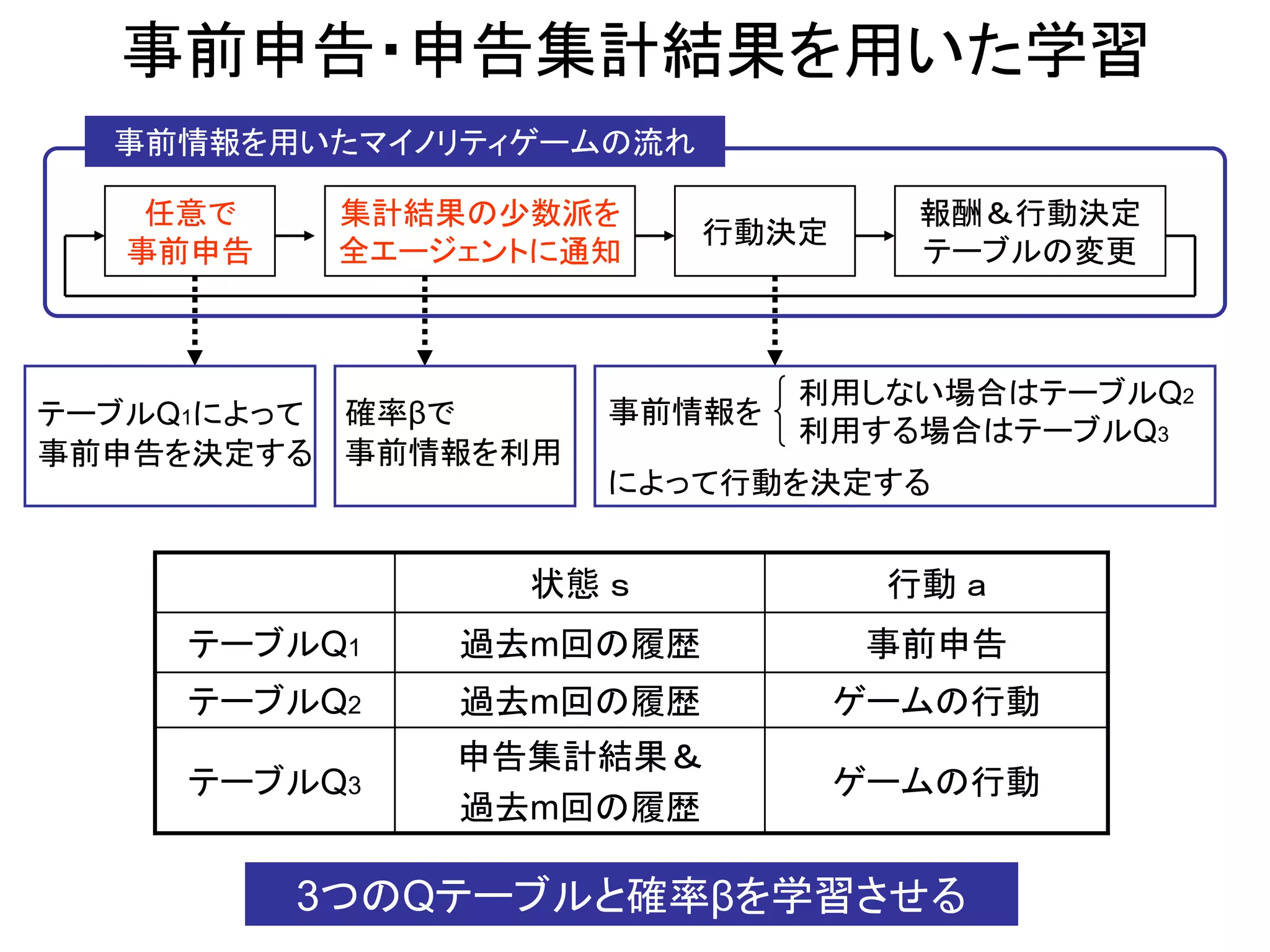
11. 12. 事前申告・申告集計結果を用いた学習
事前情報を用いたマイノリティゲームの流れ
任意で 集計結果の少数派を 報酬&行動決定
行動決定
事前申告 全エージェントに通知 テーブルの変更
利用しない場合はテーブルQ2
テーブルQ1によって 確率βで 事前情報を
利用する場合はテーブルQ3
事前申告を決定する 事前情報を利用
によって行動を決定する
状態 s 行動 a
テーブルQ1 過去m回の履歴 事前申告
テーブルQ2 過去m回の履歴 ゲームの行動
申告集計結果&
テーブルQ3 ゲームの行動
過去m回の履歴
3つのQテーブルと確率βを学習させる
13. Qテーブルとβの学習方法
行動価値関数 Q学習:利用した行動価値関数を更新
Q( st , at ) Q( st , at ) α reward ta1 max Q( st 1 , at 1 ) Q( st , at )]
[
実験設定 Q学習の学習率 α=0.1
割引率 γ=0.0
申告集計結果の利用率β
0.05 if 申告集計結果を 利用して成功 or 利用しないで失敗
0.05 if 申告集計結果を 利用して失敗 or 利用しないで成功
実験設定 βの初期値=1.0
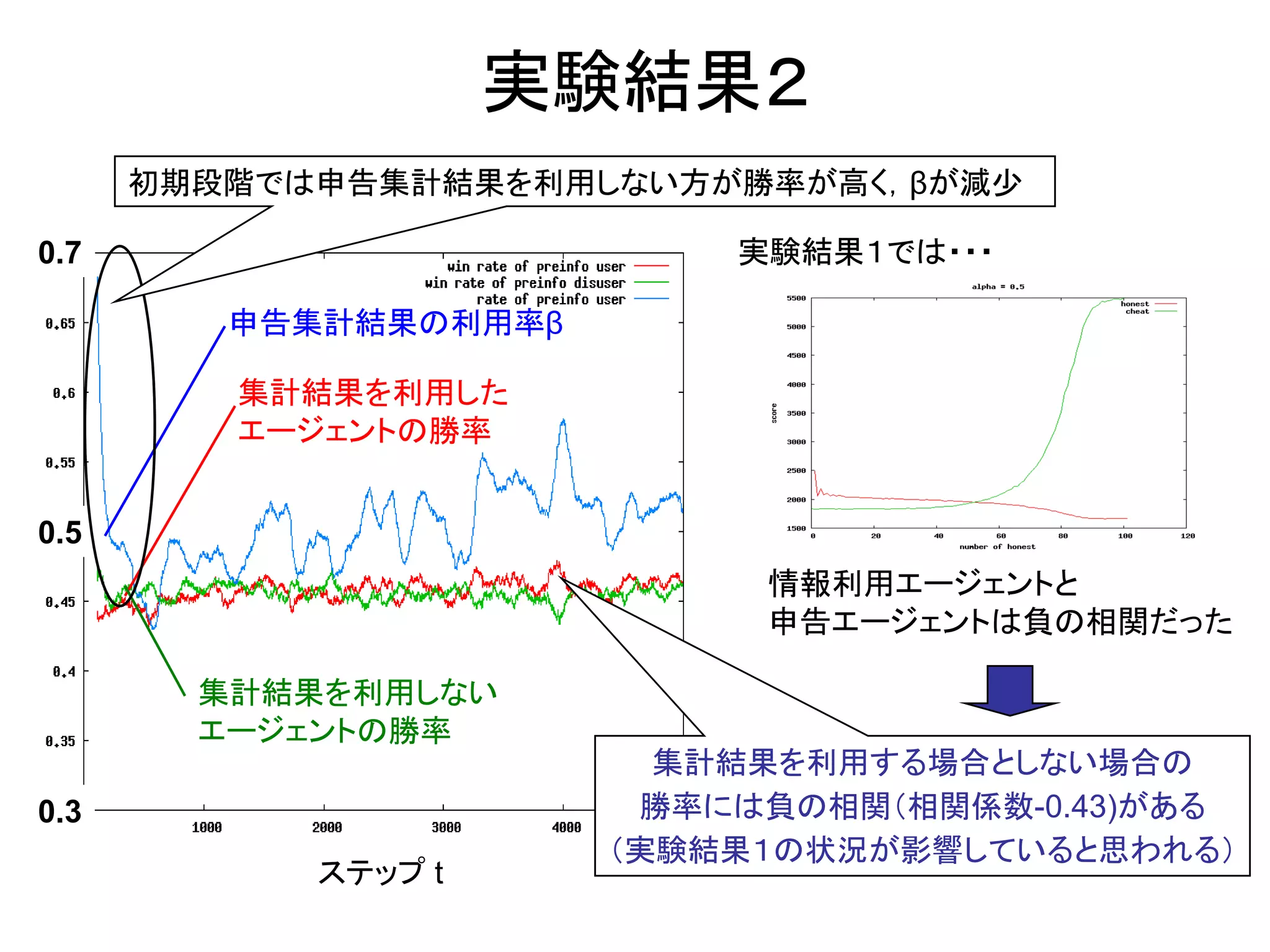
14. 実験結果2
初期段階では申告集計結果を利用しない方が勝率が高く,βが減少
0.7 実験結果1では・・・
申告集計結果の利用率β
集計結果を利用した
エージェントの勝率
0.5
情報利用エージェントと
申告エージェントは負の相関だった
集計結果を利用しない
エージェントの勝率
集計結果を利用する場合としない場合の
0.3 勝率には負の相関(相関係数-0.43)がある
(実験結果1の状況が影響していると思われる)
ステップ t
15.

![目的
マイノリティゲームに関する先行研究
•StandardMGの研究(C-.Zhang 1997)
•人工市場のシンプルなモデルとしてのマイノリティゲーム
•進化的アルゴリズムは人工市場にふさわしいか[和泉 2004]
•エージェントの学習に「進化的アルゴリズム」を用いた研究
従来のMGではエージェントの行動はゲームの履歴だけで決定
現実にはうわさ,予想などの事前情報も考えて行動する
事前情報を含んだマイノリティゲームの提案
事前情報が行動に与える影響の分析
複雑系の側面をもつ株式市場をモデル化したマイノリティゲームを用いて,
事前情報が戦略の異なる複数の利己的エージェントの行動に与える影響を解析する](https://image.slidesharecdn.com/pptgodog-130328193404-phpapp01/75/Ppt-godo-g-3-2048.jpg)
![行動決定テーブルを用いたマルチエージェントモデル
[和泉, et al., 04]
少数派だった行動
1 t-3 t-2 t-1 t
過去のゲームの履歴 A ・・・ B B A ?
各エージェントの行動でゲームをする
記憶長 m=2 の場合
報酬の獲得,行動決定テーブルの更新
t-2 t-1 t
報酬 行動決定テーブルの更新
A A P1
少数派 R 変更なし
A B P2 多数派 無し 確率α P3 ← P3
B A P3 確率1-α 変更なし
B B P4
行動決定テーブル 再びゲームをする](https://image.slidesharecdn.com/pptgodog-130328193404-phpapp01/75/Ppt-godo-g-4-2048.jpg)

![Qテーブルとβの学習方法
行動価値関数 Q学習:利用した行動価値関数を更新
Q( st , at ) Q( st , at ) α reward ta1 max Q( st 1 , at 1 ) Q( st , at )]
[
実験設定 Q学習の学習率 α=0.1
割引率 γ=0.0
申告集計結果の利用率β
0.05 if 申告集計結果を 利用して成功 or 利用しないで失敗
0.05 if 申告集計結果を 利用して失敗 or 利用しないで成功
実験設定 βの初期値=1.0](https://image.slidesharecdn.com/pptgodog-130328193404-phpapp01/75/Ppt-godo-g-13-2048.jpg)