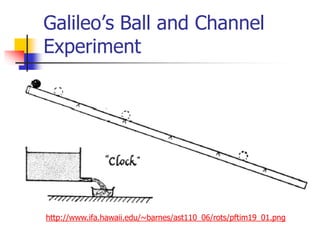
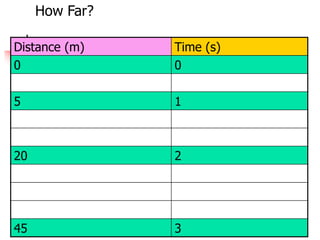
This document discusses free fall and Galileo's experiments. It begins by asking questions about whether heavier objects fall faster, the role of air resistance, the acceleration due to gravity, and how to solve free fall problems. It then discusses Galileo's experiments dropping objects from the Leaning Tower of Pisa and using a ball and channel to show that the acceleration of falling objects is constant and independent of mass. It provides the equations to calculate distance, time, velocity and acceleration for objects in free fall. It includes examples of calculating values for a ball dropped from a building and a hammer dropped on the moon.

1. Free Fall
Physics
Mr. Berman
Stuntman’s Free Fall – Great Adventure 2004

2. Questions:
 Do heavier objects fall faster than lighter
ones when starting from the same
position?
 Does air resistance matter?
 If the free fall motion has a constant
acceleration, what is this acceleration and
how was it found?
 How do we solve problems involving free
fall?

3. Apollo 15 -Astronaut David
Scott on the Moon (1971)
 Hammer and Feather on the Moon
 http://www.archive.org/details/NIX-LV-1998-
00046

4. Galileo (1564 –
1642) and the
leaning tower of
Pisa.

5. Does Air Resistance Matter?

6. Air Resistance
 The force of friction or drag acting on
an object in a direction opposing its
motion as it moves through air.

7. Hammer & Feather in the
presence of air

8. Hammer & Feather in the
absence of air

9.  If the free fall motion has a constant
acceleration, what is this acceleration
and how was it found?

10. Galileo’s Ball and Channel
Experiment
http://www.ifa.hawaii.edu/~barnes/ast110_06/rots/pftim19_01.png

11. Galileo’s Ball and Channel
Experiment
 He varied the starting position of the ball
along the channel.
 He measured the times for the ball to travel
the various lengths.
 He raised the channel until it was steep
enough to simulate free fall.

12. Galileo’s Finding
 “ We compared the time for the whole length
with that for the half, or with that for two-thirds,
or three-fourths, or indeed for any fraction; in
such experiments, repeated a full hundred times,
we always found that the spaces traversed were
to each other as the squares of the times, and
this was true for all inclinations of the plane, i.e.,
of the channel, along which we rolled the ball.
Galileo “Two New Sciences”
 http://galileoandeinstein.physics.virginia.edu/lect
ures/gal_accn96.htm

13. Distance (m) Time (s)
0 0
5 1
20 2
45 3
How Far?

14. To Find Distance from t and g:
d=vit + ½ g t2

15. How Fast?

16. Acceleration due to Gravity, g
 g=-9.8m/s2 (we often use -10m/s2)
g= v f –v i
t
 When vi=0: vf=gt
 Note: the down direction is usually
assumed negative.

17. Equations
of Motion
for Uniform
Accelerated
Motion
vf= vi+ gt
vavg = ½ (vf +vi)
d= ½ (vf + vi)t
d= vit + ½ gt2
vf
2 = vi
2 + 2gd
 d is the displacement (or
Δd)
 Assume that ti=0

18. Example 1: Free Fall
A ball is dropped from rest from the top of
a building. Find:
a) The instantaneous velocity of the ball after
6 sec.
b) How far the ball fell.
c) The average velocity up to that point.
Answers: -60m/s, 180m, -30m/s

19. Example 2: Free Fall on the Moon
A hammer is dropped on the moon. It reaches the
ground 1s later. If the distance it fell was 0.83m:
1. Calculate the acceleration due to gravity on the
surface of the moon.
2. Calculate the velocity with which the hammer
reached the ground and compare to the velocity it
would have, if it was dropped on the earth’s
surface.
Answer:-1.66m/s2, -1.66m/s, -9.8m/s