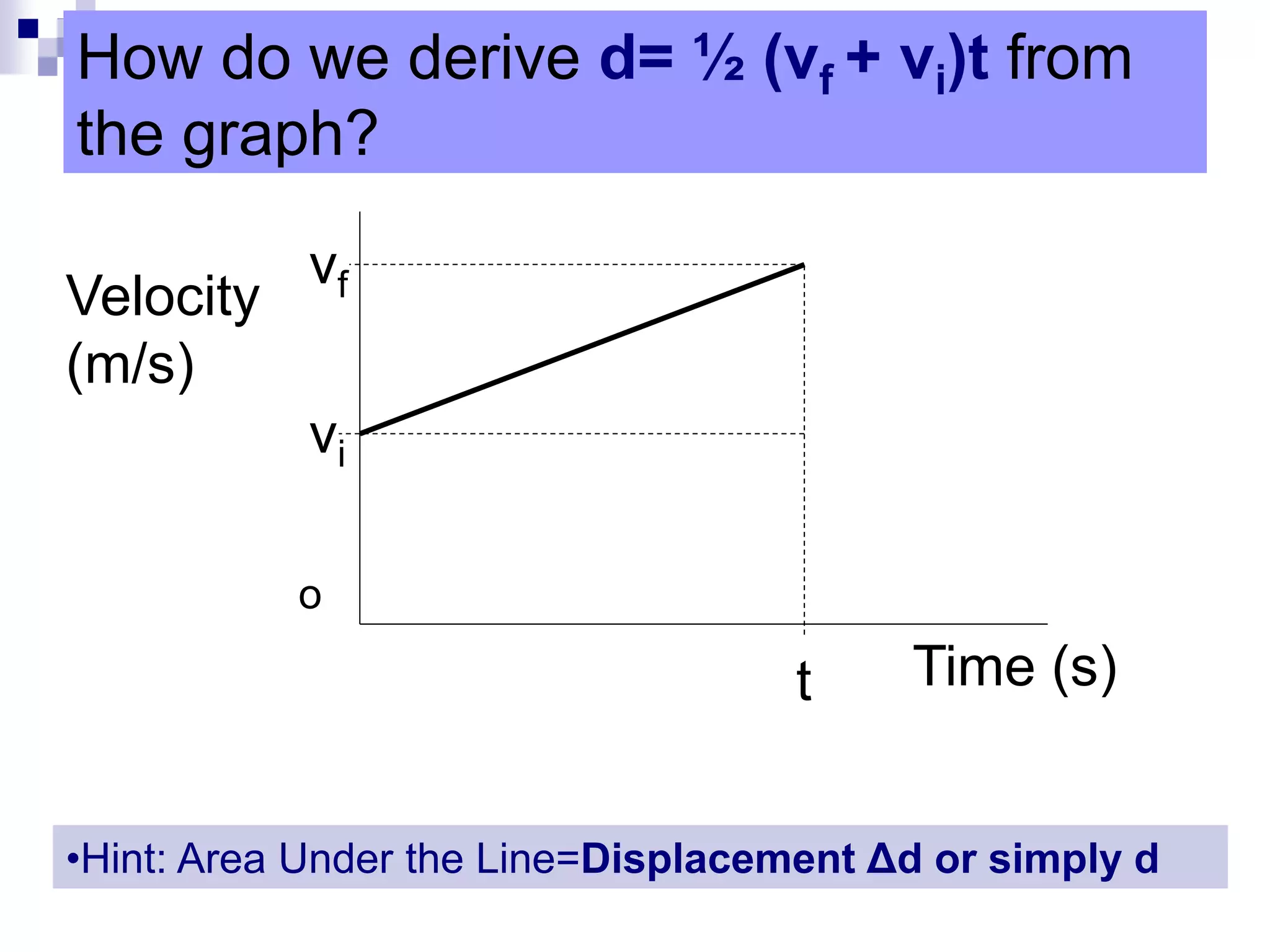
This document discusses equations of uniform accelerated motion, including average velocity, displacement, final velocity, and how to derive various kinematic equations. It also provides instructions on how to set up and solve kinematics problems using the appropriate equations. Three sample kinematics problems are worked out using the equations of uniform accelerated motion.

1. Equations of Uniform
Accelerated Motion
Physics
Mr. Berman

2. Average Velocity
v = ½ (vf +vi)

3. •Displacement in terms of Average
Velocity and Time
d= v t
d= ½ (vf + vi) t

4. How do we derive d= ½ (vf + vi)t from
the graph?
Time (s)
o
Velocity
(m/s)
•Hint: Area Under the Line=Displacement Δd or simply d
vf
vi
t

5. Displacement (d) in terms of vi , a, t
d= vit + ½ at2

6. How do we derive d= vit + ½ at2 ?
Hint: Start with d= ½ (vf + vi)t and then
substitute for vf that vf = vi+at.

7. •Final Velocity in terms of vi, a, d
vf
2 = vi
2 + 2ad

8. How do we derive vf
2 = vi
2 + 2ad ?
 Hint: Start with d= ½ (vf + vi)t and then
substitute for t = (vf – vi) /a .

9. Equations
of Motion
for Uniform
Accelerated
Motion
vf= vi+ at
vavg = ½ (vf +vi)
d= ½ (vf + vi)t
d= vit + ½ at2
vf
2 = vi
2 + 2ad
 d is the displacement (or
Δd)
 Assume that ti=0

10. Solving Kinematics Problems
 Draw a labeled vector diagram showing the
positive and negative direction.
 Make a list of the givens (include signs as
needed) and unknown.
 Decide what equation(s) you should use.
 Write the equation(s) and solve for the
unknown. Always include units in your first
substitution and in your final answer.

11. Problem 1
A rocket travelling at +95m/s is
accelerated uniformly to +150m/s in 10s.
What is the displacement?
Answer:1,225.m

12. Problem 2
An airplane has a minimum take off
velocity of 80m/s. How long should the
runway be, if the airplane can accelerate
on the ground at 3m/s2 ?
Answer: 1,067m

13. Problem 3
An airplane landing at +100m/s, comes to
a stop in 30s.
1. What is the acceleration?
2. How far did it travel on the runway before it
stopped?
Answer: -3.3m/s2, 1,515m