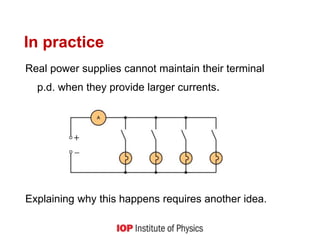
This document provides an overview of key concepts related to electric circuits, including: 1) Describing the differences between direct and alternating currents, and discussing challenges students face distinguishing between voltage and current. 2) Explaining how batteries supply energy to a circuit by transferring energy to charges located in circuit components like filaments, in accordance with the law of conservation of energy. 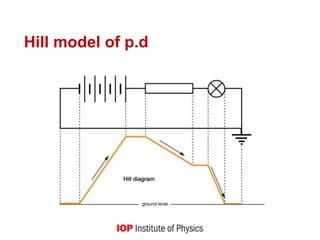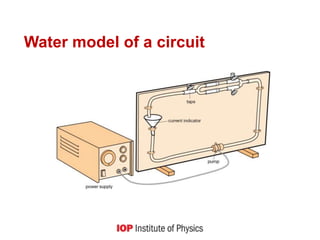3) Discussing models used to represent circuits, including water and hill models, and how more accurate representations show batteries maintaining electric fields. 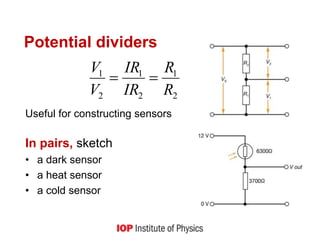4) Defining concepts like electromotive force, potential difference, resistance, and how these relate to determining current and power in both simple and complex circuit configurations.

1. Potential difference &
resistance

2. Learning outcomes
• describe the difference between direct and alternating currents
• apply the law of conservation of energy to simple circuits
• use concepts of electric potential energy, electromotive force and
potential difference to describe DC circuits
• predict the behaviour of resistors in series and parallel and be able to
calculate effective resistances
• recognise and use variable resistors, LDRs, LEDs, thermistors
• use the relationship between power, potential difference and current to
analyse simple circuits
• explain how fuses protect electrical appliances & calculate fuse values
• critically use a variety of models to show how energy is transferred in
simple circuits
• develop confidence with electrical equipment: use ammeters,
voltmeters and multimeters in simple circuits

3. Teaching challenges
Once students grasp the idea of an electric current,
they find it difficult to accept the need for another
measure of electricity (voltage, potential difference).
It doesn’t help that voltmeters and ammeters look so
similar.

4. Charge and current
Charge is a fundamental property (of protons and
electrons). Charge is conserved.
Current is the rate of flow of charge past a point.
I = current in A, Q = charge in C, t = time in s
Current in a wire (SPT simulations)
electron drift
conventional current
t
Q
I


 t
I
Q 



5. AC and DC
Direct current – always in one
direction, though flow rate
may change e.g. a pulsed
current.
Alternating current – flow
direction changes with time.
Flow rate may also change.

6. Circuits: the energy story
KS2: A battery gives electrical ‘push’ to electrons in a circuit.
KS3/4: A battery gives electrical ‘push and pull’ to electrons in a
circuit.
Better: A battery is a chemical store of energy. When connected in
a circuit, it transfers energy to a circuit component by doing work
on charges located there e.g. in a filament.
Law of conservation of energy: energy supplied = work done in
the external circuit (some always dissipated as heating).

7. Lamp brightness comparison
Lamps in series,
same current.
Brightness indicates
power.
Q
E
t
Q
t
E
I
P
V 



8. Hill model of p.d

9. Water model of a circuit

10. Other models for circuits
In pairs, do the C21 Activity Models of electric circuits.
Supplementary powerpoint: teaching models found in
school textbooks, collected by Robin Millar, University
of York.

11. EMF and potential difference
A-level: A battery maintains an electric field through the circuit.
This enables it to do work on charges wherever there is a
potential difference e.g. in a filament.
Electromotive force is the energy supplied per unit
charge. (work done on each coulomb of charge)
Potential difference (p.d.) is the energy transferred per
unit charge between two points in a circuit .
(work done by each coulomb of charge)
Unit (for both) is the volt = joule/coulomb; 1 V = 1 J/C

12. Sources of EMF
chemical cell
dynamo
mains (dynamo at a power station)
photovoltaic cell (solar cell)
piezoelectric crystal (gaslighter)
EMFs can be added
in series
in parallel

13. Resistance
When the same p.d. is applied across different
conductors, different currents flow.
Resistance R of a conductor is defined as the ratio of
the potential difference V applied across it to the
current I flowing through it.
unit: ohm 
I
V
R 

14. Current, voltage and resistance
Current in a simple circuit will be larger if
• voltage of the supply is larger
• resistance in the circuit is smaller
where R is resistance,  is resistivity of the material, l is its length
and A is its cross-sectional area.
The same relationships apply in networks of identical
resistors.
A
l
R



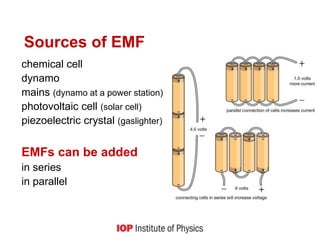
15. Resistor networks
Resistors in series
V = V1+ V2 [conservation of energy]
IR = IR1 + IR2
R = R1 + R2 R is always larger than any of R1, R2 etc
Resistors in parallel
I = I1 + I2 [conservation of charge]
V/R = V/R1 + V/R2
1/R = 1/R1 + 1/R2 R is always smaller than any of R1, R2 etc

16. Combining resistors
A practical exercise, in pairs.
Multimeter: set on resistance range.
Black lead from COM terminal
Red lead from terminal
Use breadboard to configure resistors temporarily.
NOTE: Each column of 5 holes is connected together.

17. Ohmic & non-ohmic conductors
• An ohmic conductor has a straight-line graph that
passes through the origin (I proportional to V)
• Resistance is always the ratio of V to I, not the
gradient of the I - V graph.
Ohm (1826): replaced voltaic pile with thermocouple as his source
of EMF. ‘At constant temperature, the p.d. across a conductor is
proportional to the current through it.’

18. Electrical power and fuses
Heating effect of current
(Joule, 1841, coil of wire in a jar of water)
P = IV = I2R
Fuse action:
e.g. If live wire contacts the
metal body of a kettle, the body is connected
to earth, so this produces a current surge and fuse (wire) melts,
isolating the appliance from live wire (supply).
Fuse value: Use appliance power and mains voltage to calculate its
normal current. I = P/ V Select next higher fuse rating.
Electrical fire hazard when current is too large.

19. Component characteristics
The electrical behaviour of a component is described by
its I-V graph.
For example:
I/V characteristic of a carbon resistor
I/V characteristic of a filament lamp
I/V characteristic of a semiconductor diode

20. Practical session
1. Component characteristics. Collect data and draw the
I/ V graph for resistor, lamp and diode.
2. Investigate how the resistance of LDR and thermistor
vary.
3. Experiments with SEP Energymeter
– Getting to know the joule and the watt
– Using an energymeter to measure efficiency of energy
transfer
– Using an energymeter to measure power in electrical circuits

21. Potential dividers
Useful for constructing sensors
In pairs, sketch
• a dark sensor
• a heat sensor
• a cold sensor
2
1
2
1
2
1
R
R
IR
IR
V
V



22. Electrical energy
Power is the rate of energy transfer
P = E/ t
so E = Pt = IVt
units of electrical energy: kW-hr or joules
Paying for electricity: cost per metered kW-hr

23. Problem-solving
Do any (all) of
• McDermott Physics by Inquiry Exercises
• Physics for You questions on Circuits
• TAP 109-3: Lamp and resistor in series
• Breithaupt questions from sections 13.3 Potential difference,
13.4 Resistance
Standard procedure for quantitative problems: Sketch the
circuit, write down known quantities, start with an equation in
symbols, show all working, include units with the answer.

24. ICT investigating circuits
For example,
PhET Circuit Construction Kit (DC only)

25. In practice
Real power supplies cannot maintain their terminal
p.d. when they provide larger currents.
Explaining why this happens requires another idea.

26. Support, references
www.talkphysics.org
SPT 11-14 Electricity & Magnetism
Ep4 Getting to grips with voltage
Ep5 Electrical power: a final look
David Sang (ed, 2011) Teaching secondary physics ASE / Hodder
PhET simulations Electricity, Magnets & Circuits
Practical Physics Guidance pages e.g. Models of electric circuits