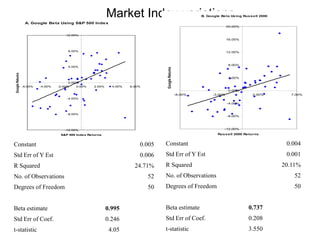
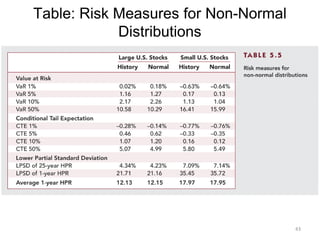
The document elaborates on portfolio theory and the Capital Asset Pricing Model (CAPM), detailing how assets are priced and the equilibrium conditions between individual investors and asset suppliers. It explains key concepts such as the risk-free asset, expected return, systematic vs. unsystematic risk, and the derivation of the CAPM equation linking expected returns to risk. Additionally, it discusses assumptions behind CAPM, the significance of beta, and the practical applications of this model in asset valuation and estimating required rates of return.

1. Portfolio Theory and Capital Asset
Pricing Model

2. Introduction
• Asset Pricing – how assets are priced?
• Equilibrium concept
• Portfolio Theory – ANY individual
investor’s optimal selection of portfolio
(partial equilibrium)
• CAPM – equilibrium of ALL individual
investors (and asset suppliers)
(general equilibrium)

3. Our expectation
• Risky asset i:
• Its price is such that:
E(return) = Risk-free rate of return + Risk premium specific to asset i
= Rf + (Market price of risk)x(quantity of risk of asset i)
CAPM tells us 1) what is the price of risk?
2) what is the risk of asset i?

4. The Risk-Free Asset
• Only the government can issue default-free
bonds
– Guaranteed real rate only if the duration of
the bond is identical to the investor’s desire
holding period
• T-bills viewed as the risk-free asset
– Less sensitive to interest rate fluctuations
4

5. • It’s possible to split investment funds
between safe and risky assets.
• Risk free asset: proxy; T-bills
• Risky asset: stock (or a portfolio)
Portfolio Theory: Portfolios of One Risky
Asset and a Risk-Free Asset
5

6. An example to motivate
Expected Return Standard Deviation
Asset i 10.9% 4.45%
Asset j 5.4% 7.25%
E(return) = Risk-free rate of return + Risk premium specific to asset i
= Rf + (Market price of risk)x(quantity of risk of asset i)
Question: According to the above equation, given that asset j has higher risk
relative to asset i, why wouldn’t asset j has higher expected return as well?
Possible Answers: (1) the equation, as intuitive as it is, is completely
wrong.
(2) the equation is right. But market price of risk is
different for different assets.
(3) the equation is right. But quantity of risk of any
risky asset is not equal to the standard deviation of
its return.

7. CAPM’s Answers
E(return) = Risk-free rate of return + Risk premium specific to asset i
= Rf + (Market price of risk)x(quantity of risk of asset i)
• The intuitive equation is right.
• The equilibrium price of risk is the same
across all marketable assets
• In the equation, the quantity of risk of any
asset, however, is only PART of the total
risk (s.d) of the asset.

8. CAPM’s Answers
• Specifically:
Total risk = systematic risk + unsystematic risk
CAPM says:
(1)Unsystematic risk can be diversified away. Since there is
no free lunch, if there is something you bear but can be
avoided by diversifying at NO cost, the market will not
reward the holder of unsystematic risk at all.
(2)Systematic risk cannot be diversified away without cost.
In other words, investors need to be compensated by a
certain risk premium for bearing systematic risk.

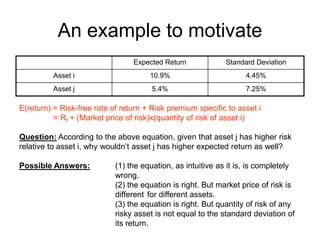
9. CAPM results
E(return) = Risk-free rate of return + Risk premium specific to asset i
= Rf + (Market price of risk)x(quantity of risk of asset i)
Precisely:
[1] Expected Return on asset i = E(Ri)
[2] Equilibrium Risk-free rate of return = Rf
[3] Quantity of risk of asset i = COV(Ri, RM)/Var(RM)
[4] Market Price of risk = [E(RM)-Rf]
Thus, the equation known as the Capital Asset Pricing Model:
E(Ri) = Rf + [E(RM)-Rf] x [COV(Ri, RM)/Var(RM)]
Where [COV(Ri, RM)/Var(RM)] is also known as BETA of asset I
Or
E(Ri) = Rf + [E(RM)-Rf] x βi

10. Pictorial Result of CAPM
E(Ri)
E(RM)
Rf
Security
Market
Line
β =
[COV(Ri, RM)/Var(RM)]βΜ= 1.0
slope = [E(RM) - Rf] = Eqm. Price of risk

11. CAPM in Details:
What is an equilibrium?
CONDITION 1: Individual investor’s equilibrium: Max U
• Assume:
• [1] Market is frictionless
=> borrowing rate = lending rate
=> linear efficient set in the return-risk space
[2] Anyone can borrow or lend unlimited amount at risk-free rate
• [3] All investors have homogenous beliefs
=> they perceive identical distribution of expected returns on
ALL assets
=> thus, they all perceive the SAME linear efficient set (we
called the line: CAPITAL MARKET LINE
=> the tangency point is the MARKET PORTFOLIO

12. CAPM in Details:
What is an equilibrium?
CONDITION 1: Individual investor’s equilibrium: Max U
Rf
A
Market Portfolio
Q
B
Capital Market Line
σp
E(Rp)
E(RM)
σM

13. CAPM in Details:
What is an equilibrium?
CONDITION 2: Demand = Supply for ALL risky assets
• Remember expected return is a function of price.
• Market price of any asset is such that its expected return is just
enough to compensate its investors to rationally hold it.
CONDITION 3: Equilibrium weight of any risky assets
• The Market portfolio consists of all risky assets.
• Market value of any asset i (Vi) = PixQi
• Market portfolio has a value of ∑iVi
• Market portfolio has N risky assets, each with a weight of wi
Such that
wi = Vi / ∑iVi for all i

14. CAPM in Details:
What is an equilibrium?
CONDITION 4: Aggregate borrowing = Aggregate lending
• Risk-free rate is not exogenously given, but is determined by
equating aggregate borrowing and aggregate lending.

15. CAPM in Details:
What is an equilibrium?
Two-Fund Separation:
Given the assumptions of frictionless market, unlimited lending and
borrowing, homogenous beliefs, and if the above 4 equilibrium
conditions are satisfied, we then have the 2-fund separation.
TWO-FUND SEPARATION:
Each investor will have a utility-maximizing portfolio that is a
combination of the risk-free asset and a portfolio (or fund) of risky
assets that is determined by the Capital market line tangent to the
investor’s efficient set of risky assets
Analogy of Two-fund separation
Fisher Separation Theorem in a world of certainty

16. • The relationship depends on the correlation
coefficient
• -1.0 < ρ < +1.0
• The smaller the correlation, the greater the
risk reduction potential
• If ρ = +1.0, no risk reduction is possible
Correlation Effects

17. The Sharpe Ratio
• Maximize the slope of the CAL for any
possible portfolio, p
• The objective function is the slope:
( )P f
P
P
E r r
S
σ
−
=
17

18. Figure: The Variance of an Equally Weighted Portfolio with Risk Coefficient βp in the
Single-Factor Economy
18

19. CAPM in Details:
What is an equilibrium?
Two-fund separation
Rf
A
Market Portfolio
Q
B
Capital Market Line
σp
E(Rp)
E(RM)
σM

20. The Role of Capital Market
Efficient set
U’’ U’
P
Endowment Point
E(rp)
σp

21. Borrow at the Risk-Free Rate and invest in
stock.
Using 50% Leverage,
rc = (-.5) (.07) + (1.5) (.15) = .19
σc = (1.5) (.22) = .33
Capital Allocation Line with Leverage
21

22. The Role of Capital Market
Efficient set
U’’’ U’’ U’
P
Endowment Point
E(rp)
σp
M
U-Max Point
Capital Market Line
Rf

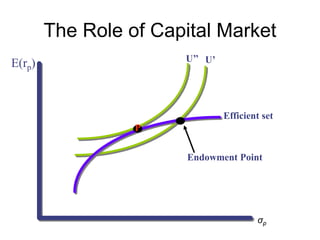
23. CAPM
• 2 sets of Assumptions:
[1] Perfect market:
• Frictionless, and perfect information
• No imperfections like tax, regulations, restrictions to short
selling
• All assets are publicly traded and perfectly divisible
• Perfect competition – everyone is a price-taker
[2] Investors:
• Same one-period horizon
• Rational, and maximize expected utility over a mean-
variance space
• Homogenous beliefs

24. Derivation of CAPM
• Using equilibrium condition 3
wi = Vi / ∑iVi for all i
market value of individual assets (asset i)
wi = ------------------------------------------------
market value of all assets (market portfolio)
• Consider the following portfolio:
hold a% in asset i
and (1-a%) in the market portfolio

25. Derivation of CAPM
• The expected return and standard deviation of such a
portfolio can be written as:
E(Rp) = aE(Ri) + (1-a)E(Rm)
σ(Rp) = [ a2σi
2 + (1-a)2σm
2 + 2a (1-a) σim ] 1/2
• Since the market portfolio already contains asset i and,
most importantly, the equilibrium value weight is wi
• therefore, the percent a in the above equations represent
excess demands for a risky asset
• We know from equilibrium condition 2 that in equilibrium,
Demand = Supply for all asset.
• Therefore, a = 0 has to be true in equilibrium.

26. Derivation of CAPM
E(Rp) = aE(Ri) + (1-a)E(Rm)
σ(Rp) = [ a2σi
2 + (1-a)2σm
2 + 2a (1-a) σim ] 1/2
• Consider the change in the mean and standard deviation with
respect to the percentage change in the portfolio invested in
asset i
• Since a = 0 is an equilibrium for D = S, we must evaluate these
partial derivatives at a = 0
)RE(-)RE(=
a
)RE(
mi
p
∂
∂
]4a-2+2a+2-2a[*]a)-2a(1+)a-(1+a[
2
1
=
a
)R(
imim
2
m
2
m
2
i
1/2-
im
2
m
22
i
2p
σσσσσσσσ
σ
∂
∂
)RE(-)RE(=
a
)RE(
mi
p
∂
∂
σ
σσσ
m
2
mimp -
=
a
)R(
∂
∂
(evaluated at a = 0)
(evaluated at a = 0)

27. Derivation of CAPM
• the slope of the risk return trade-off evaluated at point M in
market equilibrium is
• but we know that the slope of the opportunity set at point M must
also equal the slope of the capital market line. The slope of the
capital market line is
• Therefore, setting the slope of the opportunity set equal to the
slope of the capital market line
• rearranging,
σ
σσσ
m
2
mim
mi
p
p
-
)RE(-)RE(
=
a)/R(
a)/RE(
∂∂
∂∂
σ m
fm R-)RE(
σσσσ m
fm
m
2
mim
mi R-)RE(
=
/)-(
)RE(-)RE(
]R-)R[E(+R=)RE( fm2
m
im
fi
σ
σ
(evaluated at a = 0)

28. Derivation of CAPM
• From previous page
• Rearranging
• Where
E(return) = Risk-free rate of return + Risk premium specific to asset i
E(Ri) = Rf + (Market price of risk)x(quantity of risk of asset i)
CAPM Equation
)RVAR(
)R,RCOV(
==
m
mi
2
m
im
i
σ
σβ
βifmfi ]R-)R[E(+R=)RE(
]R-)R[E(+R=)RE( fm2
m
im
fi
σ
σ

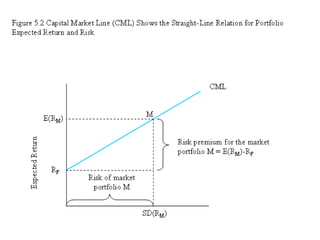
30. CML Equation
• Y = b + mX
This leads to the Security Market Line (SML)
( )
[ ]FM
M
P
F
P
M
FM
FP
RRE
RSD
RSD
R
RSD
RSD
RRE
RRE
−+=
−
+=
)(
)(
)(
givesgrearrangin
)(
)(
)(

31. SML Equation
( ) ( )
( ) ( )
( )FMiF
FM
M
Mi
F
Mi
M
FM
Fi
RRR
RR
)R(VAR
RRCOV
R
RRCOV
)R(VAR
RR
RRE
−β+=
−×+=
×
−
+=
β is a measure of relative risk
• β = 1 for the overall market.
• β = 2 for a security with twice the systematic risk of
the overall market,
• β = 0.5 for a security with one-half the systematic
risk of the market.

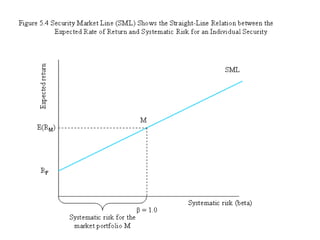
34. Pictorial Result of CAPM
E(Ri)
E(RM)
Rf
Security Market
Line
β =
[COV(Ri, RM)/Var(RM)]βΜ= 1.0
slope = [E(RM) - Rf] = Eqm. Price of risk

35. Properties of CAPM
• In equilibrium, every asset must be priced so that its risk-
adjusted required rate of return falls exactly on the security
market line.
• Total Risk = Systematic Risk + Unsystematic Risk
Systematic Risk – a measure of how the asset co-varies with
the entire economy (cannot be diversified away)
e.g., interest rate, business cycle
Unsystematic Risk – idiosyncratic shocks specific to asset i,
(can be diversified away)
e.g., loss of key contract, death of CEO
• CAPM quantifies the systematic risk of any asset as its β
• Expected return of any risky asset depends linearly on its
exposure to the market (systematic) risk, measured by β.
• Assets with a higher β require a higher risk-adjusted rate of
return. In other words, in market equilibrium, investors are only
rewarded for bearing the market risk.

36. CAPM and Portfolios
• How does adding a stock to an existing portfolio
change the risk of the portfolio?
– Standard Deviation as risk
• Correlation of new stock to every other stock
– Beta
• Simple weighted average:
• Existing portfolio has a beta of 1.1
• New stock has a beta of 1.5.
• The new portfolio would consist of 90% of the old portfolio
and 10% of the new stock
• New portfolio’s beta would be 1.14 (=0.9×1.1 + 0.1×1.5)
∑=
×=
n
i
iiP w
1
ββ

37. Estimating Beta
• Need
– Risk free rate data
– Market portfolio data
• S&P 500, DJIA, NASDAQ, etc.
– Stock return data
• Interval
– Daily, monthly, annual, etc.
• Length
– One year, five years, ten years, etc.

38. Market Index variations
Constant 0.005
Std Err of Y Est 0.006
R Squared 24.71%
No. of Observations 52
Degrees of Freedom 50
Beta estimate 0.995
Std Err of Coef. 0.246
t-statistic 4.05
Constant 0.004
Std Err of Y Est 0.001
R Squared 20.11%
No. of Observations 52
Degrees of Freedom 50
Beta estimate 0.737
Std Err of Coef. 0.208
t-statistic 3.550
A. Google Beta Using S&P 500 Index
-12.00%
-8.00%
-4.00%
0.00%
4.00%
8.00%
12.00%
-6.00% -4.00% -2.00% 0.00% 2.00% 4.00% 6.00%
S&P 500 Index Returns
GoogleReturns B. Google Beta Using Russell 2000
-12.00%
-8.00%
-4.00%
0.00%
4.00%
8.00%
12.00%
16.00%
20.00%
-8.00% -3.00% 2.00% 7.00%
Russell 2000 Returns
GoogleReturns

39. A. GM Beta Estimation: Daily Data
-25.00%
-20.00%
-15.00%
-10.00%
-5.00%
0.00%
5.00%
10.00%
15.00%
20.00%
25.00%
-25.00% -20.00% -15.00% -10.00% -5.00% 0.00% 5.00% 10.00% 15.00%
S&P 500 Returns
GMReturns Interval variations
Constant 0.0001
Std Err of Y Est 0.0002
R Squared 31.37%
No. of Observations 9591
Degrees of Freedom 9589
Beta estimate 1.047
Std Err of Coef. 0.016
t-statistic 66.26
Constant 0.019
Std Err of Y Est 0.054
R Squared 31.41%
No. of Observations 38
Degrees of Freedom 36
Beta estimate 1.301
Std Err of Coef. 0.320
t-statistic 4.06
D. GM Beta Estimate: Yearly Returns
-60.00%
-40.00%
-20.00%
0.00%
20.00%
40.00%
60.00%
80.00%
100.00%
120.00%
-30.00% -20.00% -10.00% 0.00% 10.00% 20.00% 30.00% 40.00%
S&P 500 Returns
GMReturns

40. Problems using Beta
• Which market index?
• Which time intervals?
• Time length of data?
• Non-stationary
– Beta estimates of a company change over time.
– How useful is the beta you estimate now for thinking about
the future?
• Other factors seem to have a stronger empirical
relationship between risk and return than beta
– Not allowed in CAPM theory
– Size and B/M

41. Use of CAPM
• For valuation of risky assets
• For estimating required rate of return of
risky projects

42. EXHIBIT: Geometric Mean rates of Return and Standard
Deviation for Sotheby's Indexes, S&P 500, Bond Market
Series, One-Year Bonds, and Inflation
Standard
Deviation
1-Year Bond
CPI
Amer Fum
LBGC
Cont Silver
Eng Silver
Fr+Cont Furn
UW Index
Eng Furn
Mod Paint
Cont Art
Imp Paint
Chinese
Ceramic
S&P500
Old Master
Cont
Ceramic
19C Euro
Amer Paint
FW Index
VW Index

43. Table: Risk Measures for Non-Normal
Distributions
43

44. EXHIBIT: Alternative Investment Risk and
Return Characteristics
Futures
Art and Antiques
Warrants and OptionsCoins and Stamps
Commercial Real Estate
Foreign Common Stock
US Common Stocks
Real Estate (Personal Home)Foreign Corporate Bonds
US Corporate Bonds
Foreign Government Bonds
US Government Bonds
T-Bills

45. Arbitrage Pricing Theory (APT)
45
• Assume factor model such as
• And no arbitrage opportunities exist in
equilibrium
• Then, we have
iiii eFr ++= 1βα
iirE βλλ 10)( +=

46. • APT applies to almost all individual securities
• With APT it is possible for some individual
stocks to be mispriced - not lie on the SML
• APT is more general in that it gets to an
expected return and beta relationship without
the assumption of the market portfolio
• APT can be extended to multifactor models
APT and CAPM Compared

47. Multifactor APT
• Use of more than a single factor
• Requires formation of factor portfolios
• What factors?
– Factors that are important to performance
of the general economy
– Fama-French Three Factor Model

48. Two-Factor Model
• The multifactor APT is similar to the one-
factor case
– But need to think in terms of a factor portfolio
1 1 2 2( )i i i i ir E r F F eβ β= + + +

49. Example of the Multifactor Approach
• Work of Chen, Roll, and Ross
– Chose a set of factors based on the ability
of the factors to paint a broad picture of the
macro-economy
– GDP factor, inflation factor, and interest
rate factor

50. Another Example:
Fama-French Three-Factor Model
• The factors chosen are variables that on
past evidence seem to predict average
returns well and may capture the risk
premiums
• Where:
– SMB = Small Minus Big, i.e., the return of a portfolio of small stocks in
excess of the return on a portfolio of large stocks
– HML = High Minus Low, i.e., the return of a portfolio of stocks with a
high book to-market ratio in excess of the return on a portfolio of stocks
with a low book-to-market ratio
it i iM Mt iSMB t iHML t itr R SMB HML eα β β β=+ + + +

51. The Multifactor CAPM and the APT
• A multi-index CAPM will inherit its risk factors
from sources of risk that a broad group of
investors deem important enough to hedge
• The APT is largely silent on where to look for
priced sources of risk

52. Using CAPM
• Expected Return
– If the market is expected to increase 10% and
the risk free rate is 5%, what is the expected
return of assets with beta=1.5, 0.75, and -0.5?
• Beta = 1.5; E(R) = 5% + 1.5 × (10% - 5%) = 12.5%
• Beta = 0.75; E(R) = 5% + 0.75 × (10% - 5%) = 8.75%
• Beta = -0.5; E(R) = 5% + -0.5 × (10% - 5%) = 2.5%
• Finding Undervalued Stocks…(the SML)