Uploaded byeducatecreate
KEY, PDF843 views

Pi day final version

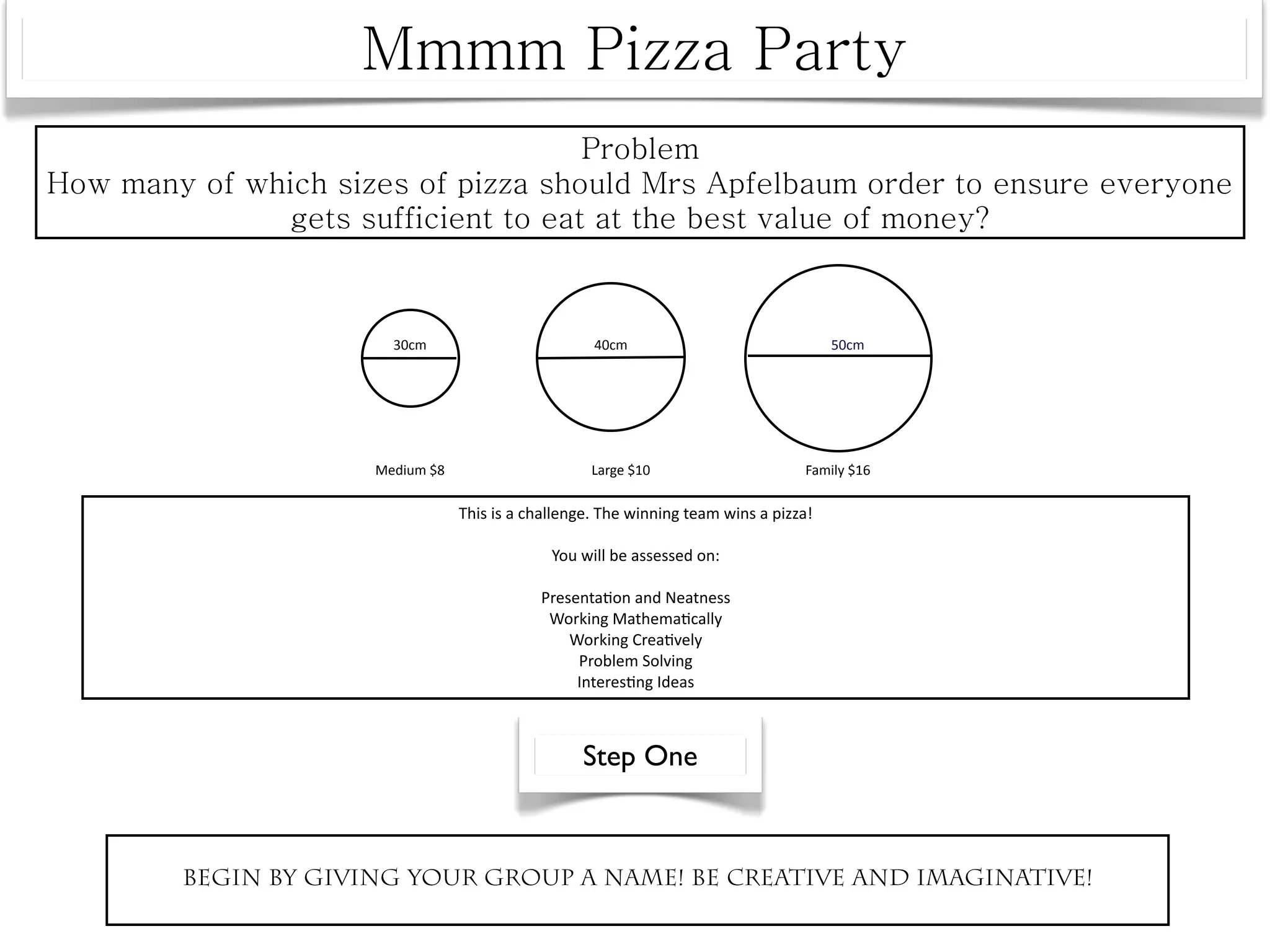
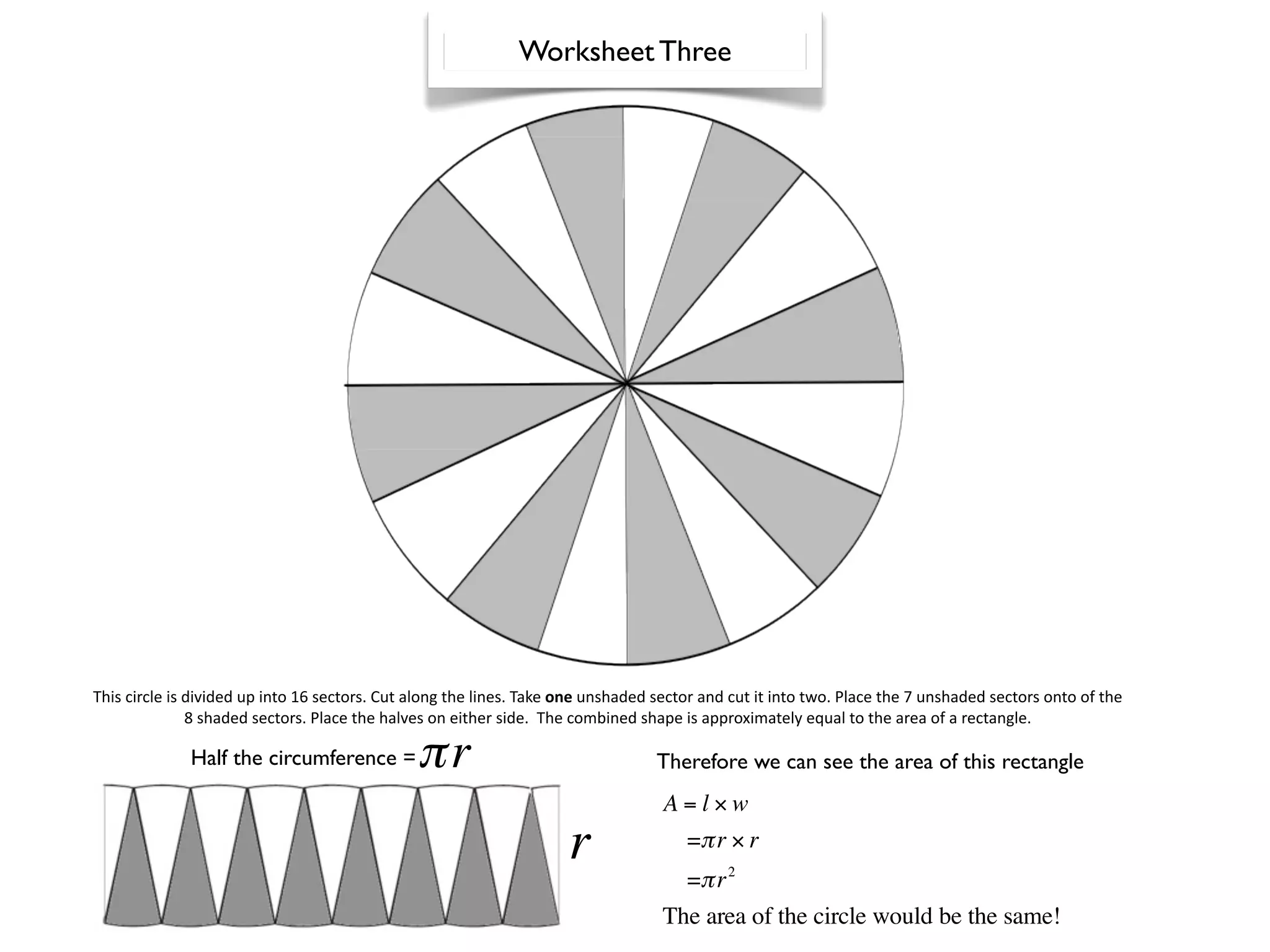
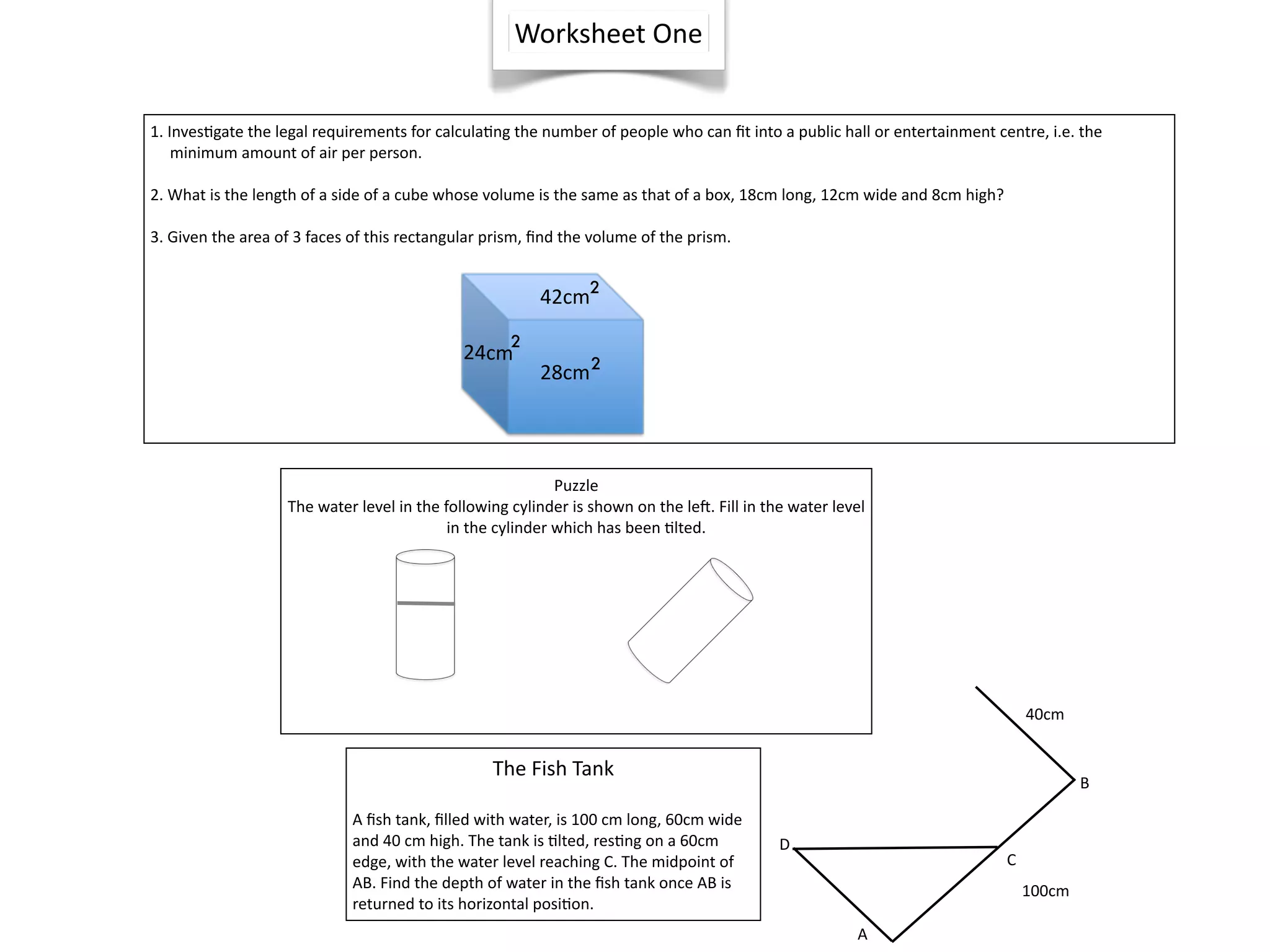
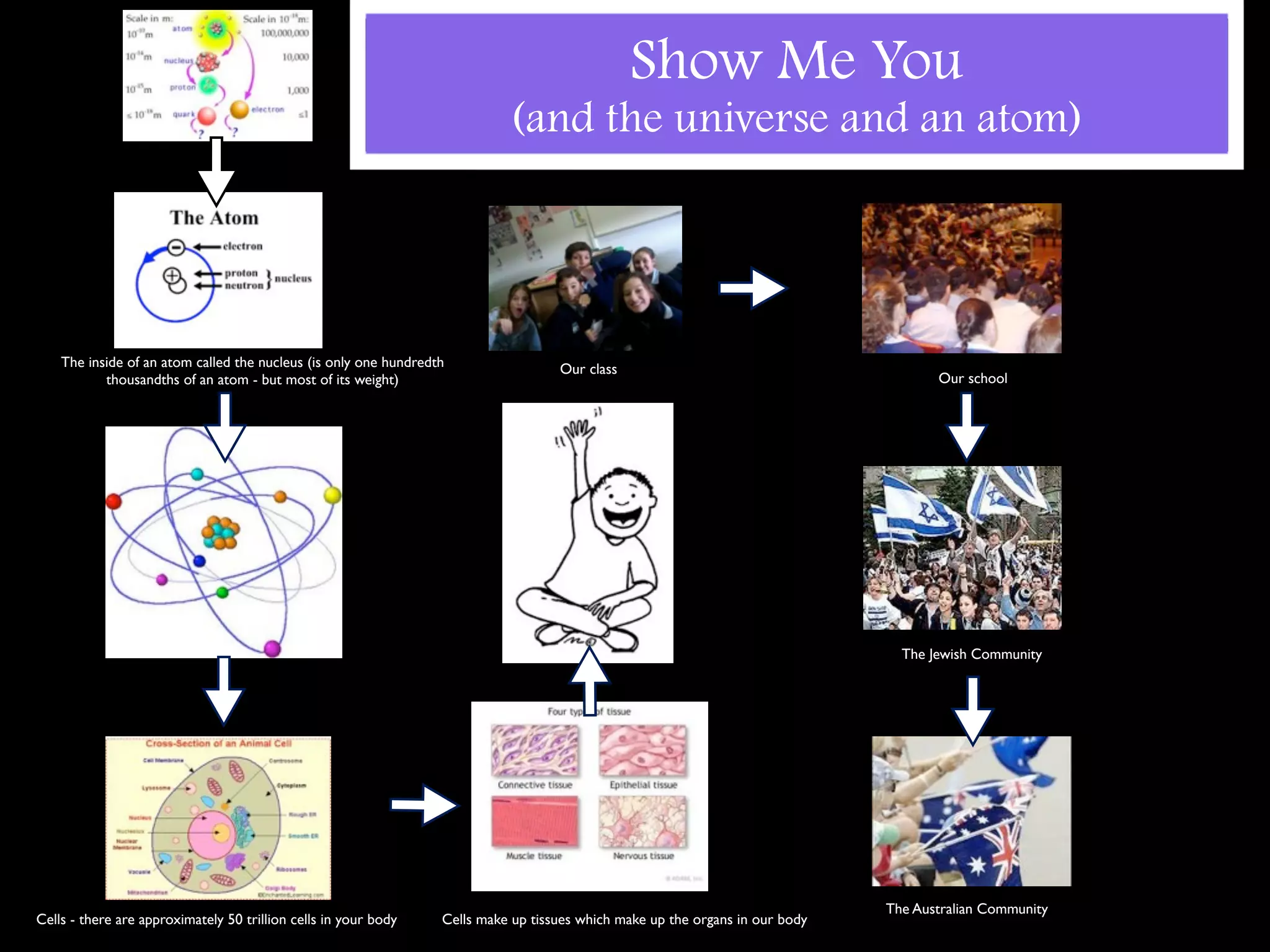
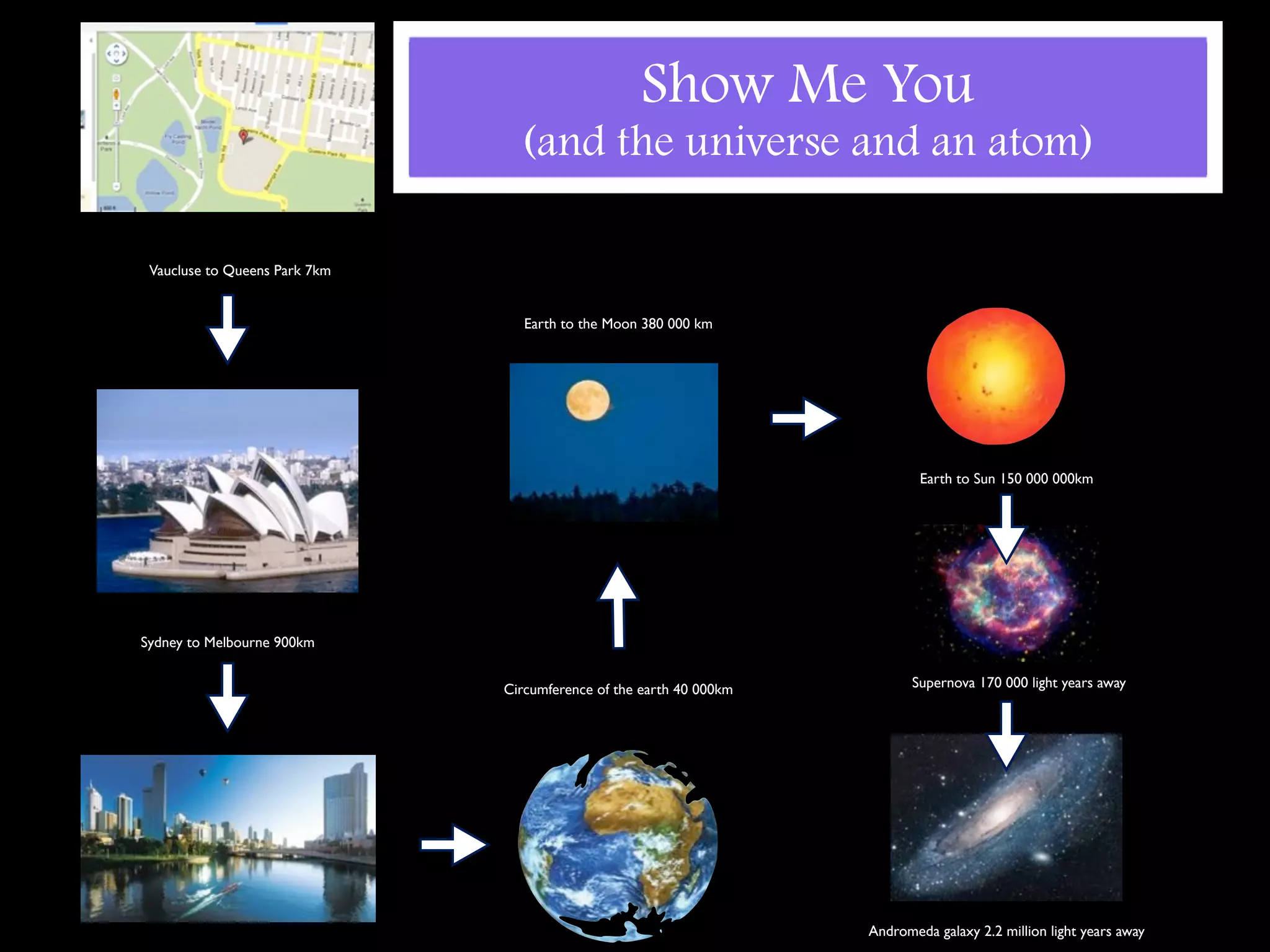
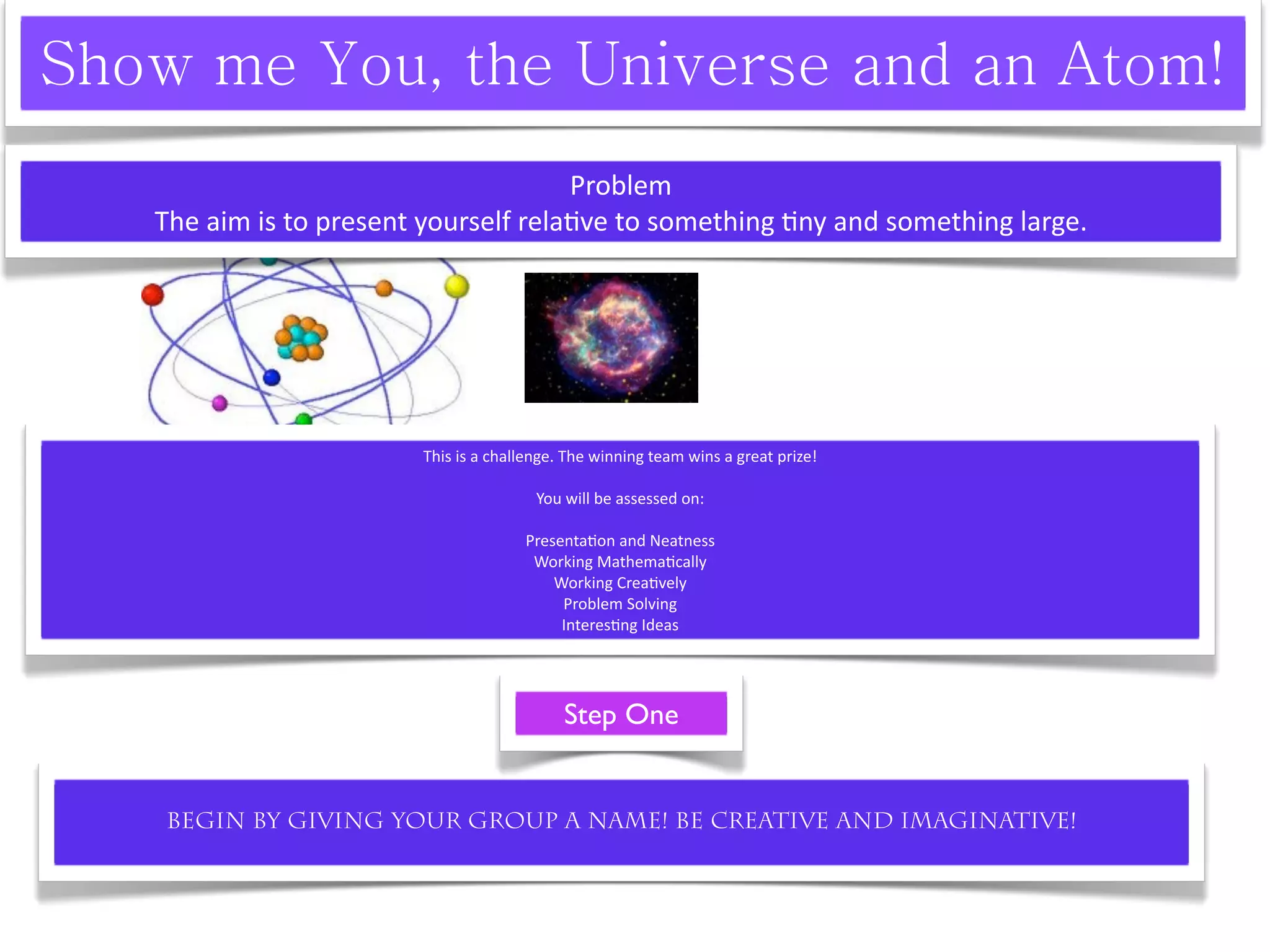
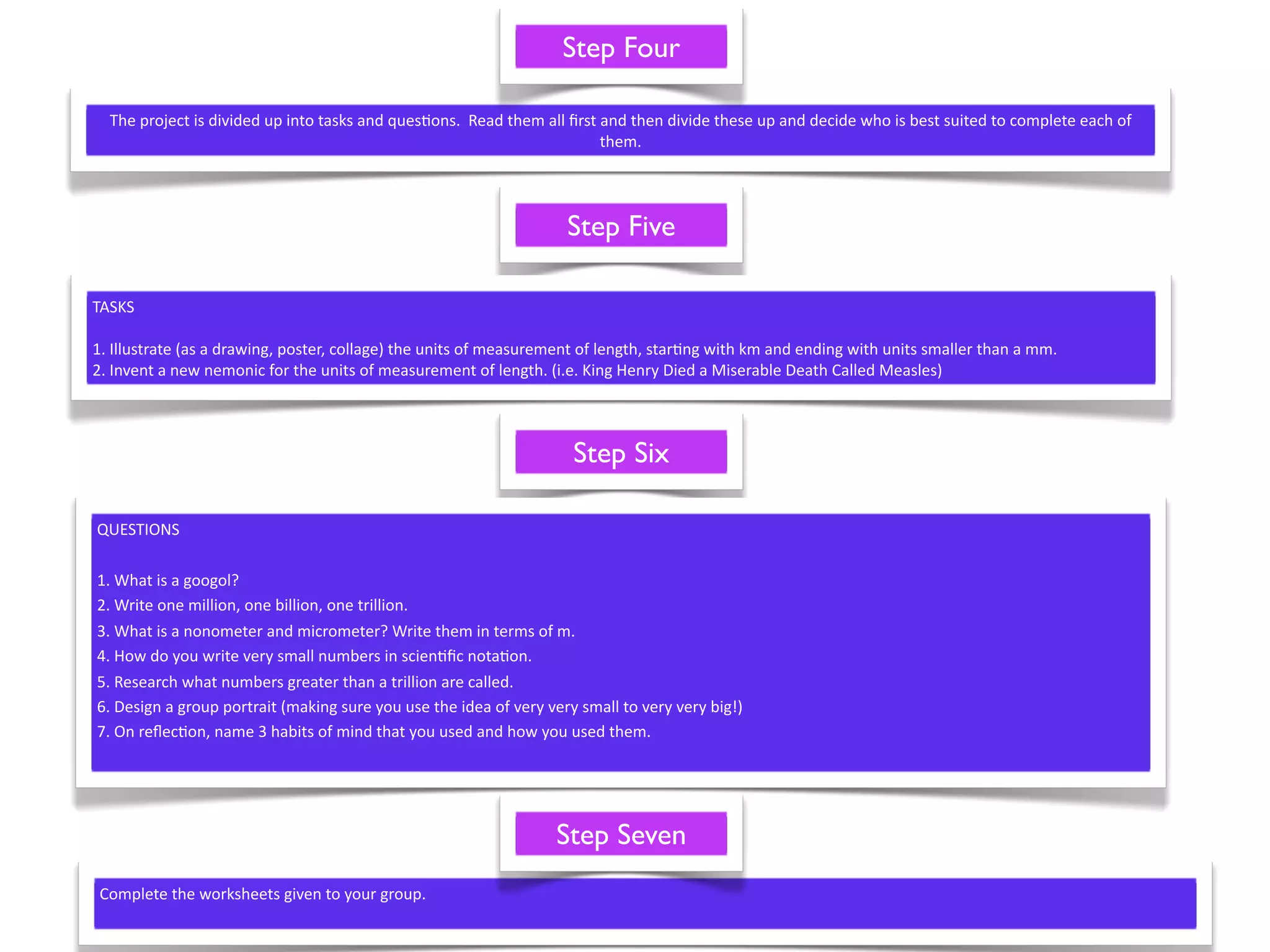
This document announces an exciting Maths Week for middle school students with various math-themed activities and competitions planned each day, including Countdown, Quizdom, and Mathematical Idol. Students in Years 6, 7, and 8 will work on a measurement project and have opportunities to win prizes for participating enthusiastically.

Embed presentation

Downloaded 15 times
ARE
YOU
READY
FOR
MATHS WEEK!
Cou ntdo matical Idol! wn! Mathe Qu izdo m!
Year 6, 7 and 8 will be doing a project on MEASUREMENT. You will be introduced to the project in the Middle School Meeting Room during your first maths lesson of the week. You will then be put into groups of 4. Each maths lesson you will go to your regular classroom and complete the project. There will be a maths riddle in Hayom every day of this week. There will be a COUNTDOWN competition for all of the Middle School during lunch on Tuesday. There will be a QUIZDOM competition during lunch on Wednesday. There will be a MATHEMATICAL IDOL during lunch on Thursday. Cou ntdo matical Idol! wn! Mathe Qu izdo m!
This is no ordinary Maths Week! The prizes are spectacular! spectacular The prize will not only be awarded to the best group in each year but also to the children who have participated the most enthusiastically! Year 7 “Clowning Around!” Year 6 “You, Me, An Atom and the Universe” Year 8 “Mmmm Pizza Party”
Mrs
Apfelbaum
is
having
a
party
for
20
people.
She
decides
to
order
some
pizzas
from
Bondi
 Pizza
for
everyone.
The
pizzas
come
in
a
choice
of
three
sizes

medium
(30cm
diameter),
large
 (40cm
diameter)
and
family
(50cm
diameter).
The
pizzas
cost
$8
for
medium,
$10
for
large
and
 $16
for
family. How
many
of
which
sizes
of
pizza
should
Mrs
Apfelbaum
order
 to
ensure
everyone
gets
sufficient
to
eat
at
the
best
value
of
 money?
This
is
a
challenge.
The
winning
team
wins
a
 30cm 40cm 50cm pizza!
 You
will
be
assessed
on: Presenta^on
and
Neatness Medium
$8 Large
$10 Family
$16 Working
Mathema^cally Begin by giving your group a name! Be creative and imaginative! Working
Crea^vely Problem
Solving Interes^ng
Ideas PLANNING You
need
to
brainstorm
this
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
 organiser
you
will
use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. TASKS 1.
What
do
you
need
to
know
before
you
begin? 1.
Cut
out
20
people
from
magazines
and
newspapers
to
represent
 




the
people
at
your
party.
(You
must
use
a
range
of
ages).
Display


 
 2.
What
do
you
need
to
do
to
solve
this
problem? 




them
neatly
in
a
poster. 3.
What
assump^ons
do
you
need
to
make? 2.
Each
group
will
be
given
a
recipe.
You
need
to
arrange
the
recipe 4.
What
do
you
predict
you
will
find? 



in
the
correct
sequence. 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering? QUESTIONS Habits of Mind you will need to complete this project: Thinking Flexibly 1.
What
is
the
area
of
each
of
the
pizzas?
(Round
to
two
decimal
places) Thinking Creatively 2.
What
is
the
circumference
of
each
of
the
pizzas?
(Round
to
two
decimal
places) Thinking Critically 3.
What
is
the
cost
per
cm
square? Persistence ο ο 4.
What
is
the
cost
of
a
slice
of
pizza
which
is
18


and
320




? Responsible Risk Taking Managing your Impulsivity 5.
How
much
would
one
slice
of
pizza
cost?
(Decide
how
many
slices
the
pizzas
should
be
cut
into.) Group Effectiveness 6.
Which
is
the
best
value? 7.
Looking
at
the
party
guests,
decide
how
much
pizza
each
person
would
eat?
Give
reasons
why? 8.
How
many
pizzas
should
Mrs
Apfelbaum
be
ordering
and
what
sizes? 9.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them.
30cm 40cm 50cm Medium
$8 Large
$10 Family
$16 This
is
a
challenge.
The
winning
team
wins
a
pizza!
 You
will
be
assessed
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
 on
a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING You
need
to
brainstorm
this
problem
and
add
how
you
thought
about
this
project
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
 use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
What
assump^ons
do
you
need
to
make? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering? Step Four The
project
is
divided
up
into
tasks,
ques^ons
and
worksheets.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
 each
of
them.


Step Five TASKS
(Choose
at
least
2
of
them) 1.
Decide
on
the
20
people
who
are
invited
to
your
party.
(You
can
even
add
some
famous
people!)
Cut
out
20
people
from
magazines
to
represent 




your
guests.
You
MUST
use
a
range
of
ages
(as
shown
in
the
keynote).
Display
them
as
crea^vely
as
you
like
in
a
poster,
collage
or
assemblage. 


 2.
Each
group
will
be
given
a
recipe
on
how
to
make
a
pizza.
You
need
to
arrange
the
recipe
into
sequen^al
order
and
paste
it
onto
a
piece
of
paper. 3.
Design
a
name
and
menu
for
a
new
pizza
place
around
the
corner! 



 Step Six QUESTIONS
(Answer
all
of
these
ques^ons) 1.
What
is
the
area
of
each
of
the
pizzas?
(Round
to
two
decimal
places) 2.
What
is
the
circumference
of
each
of
the
pizzas?
(Round
to
two
decimal
places) 3.
What
is
the
cost
per
cm
square? 4.
If
the
family
size
pizza
is
cut
into
8
slices,
how
many
square
cm
would
that
be
and
how
much
would
each
slice
cost? 5.
If
the
medium
and
large
pizza
is
cut
into
8
slices,
how
many
square
cm
would
that
be
and
how
much
would
each
slice
cost? 6.
Which
is
the
best
value? 7.
Looking
at
the
party
guests,
decide
how
much
pizza
each
person
would
eat?
Give
reasons
why?
(Be
crea^ve
with
your
answers) 8.
How
many
pizzas
should
Mrs
Apfelbaum
be
ordering
and
what
sizes? 9.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
30cm 40cm 50cm Medium
$8 Large
$10 Family
$16 This
is
a
challenge.
The
winning
team
wins
a
pizza!
 You
will
be
assessed
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
 on
a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING You
need
to
brainstorm
this
problem
and
add
how
you
thought
about
this
project
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
 use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
What
assump^ons
do
you
need
to
make? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering? Step Four The
project
is
divided
up
into
tasks,
ques^ons
and
worksheets.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
 each
of
them.


Step Five TASKS
(Choose
at
least
2
of
them) 1.
Decide
on
the
20
people
who
are
invited
to
your
party.
(You
can
even
add
some
famous
people!)
Cut
out
20
people
from
magazines
to
represent 




your
guests.
You
MUST
use
a
range
of
ages
(as
shown
in
the
keynote).
Display
them
as
crea^vely
as
you
like
in
a
poster,
collage
or
assemblage. 


 2.
Each
group
will
be
given
a
recipe
on
how
to
make
a
pizza.
You
need
to
arrange
the
recipe
into
sequen^al
order
and
paste
it
onto
a
piece
of
paper. 3.
Design
a
name
and
menu
for
a
new
pizza
place
around
the
corner! 



 Step Six QUESTIONS
(Answer
all
of
these
ques^ons) 1.
What
is
the
area
of
each
of
the
pizzas?
(Round
to
two
decimal
places) 2.
What
is
the
circumference
of
each
of
the
pizzas?
(Round
to
two
decimal
places) 3.
What
is
the
cost
per
cm
square? 4.
If
the
family
size
pizza
is
cut
into
8
slices,
how
many
square
cm
would
that
be
and
how
much
would
each
slice
cost? 5.
If
the
medium
and
large
pizza
is
cut
into
8
slices,
how
many
square
cm
would
that
be
and
how
much
would
each
slice
cost? 6.
Which
is
the
best
value? 7.
Looking
at
the
party
guests,
decide
how
much
pizza
each
person
would
eat?
Give
reasons
why?
(Be
crea^ve
with
your
answers) 8.
How
many
pizzas
should
Mrs
Apfelbaum
be
ordering
and
what
sizes? 9.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
Worksheet One What
parts
of
the
circle
are
there
in
these
prac^cal
examples? Circumference The
circumference
is
a
special
name
we
give
to
the
perimeter
of
the
circle.
 Measure
and
cut
a
string
of
length
20
cm.
Take
the
string
and
form
a
circle
by
joining
its
two
ends.
Es^mate
how
much
longer
the
circumference
is
than
the
 diameter?

Now
measure
the
diameter.
Divide
20
cm
(the
circumference)
by
the
measurement
of
the
diameter. Now,
cut
the
string
into
a
length
of
15
cm.
Again
form
a
circle
and
measure
the
diameter.
Divide
15
cm
(the
circumference)
by
the
measurement
of
the
diameter. Now,
cut
the
string
into
a
length
of
10
cm.
Again
form
a
circle
and
measure
the
diameter.
Divide
10
cm
(the
circumference)
by
the
measurement
of
the
diameter. What
have
you
found
each
^me? Pi Our
inves^ga^ons
have
shown
that
the
circumference
of
a
circle
is
just
more
than
three
^mes
the
diameter.
The
ancient
Greeks,
Egyp^ans,
Chinese
and
others
 
 π knew
about
this
special
number.
A
special
Greek
lejer









(pronounced
Pi)
stands
for C ≈ 3.14 ≈ 3 1 d 7 A
regular
hexagon
with
sides
3
cm
is
circumscribed
by
a
circle
(a
circle
is
drawn
around
the
hexagon).
Diameters
are
 drawn
to
the
ver^ces
of
the
hexagon. How
many
triangles
have
been
drawn
and
what
kind
of
triangles
are
they? What
is
the
length
of
the
diameter
of
the
circle? What
is
the
perimeter
of
the
hexagon? Is
the
circumference
of
the
circle
slightly
longer
than
the
perimeter
of
the
hexagon? Therefore
what
can
you
conclude
about
the
length
of
the
circumference
in
rela^on
to
the
length
of
the
diameter?
Worksheet Two Pi
has
a
long
history
and
the
following
is
a
short
list
of
approxima^ons
that
have
been
found
for
Pi.
The
calculator
has
Pi
as
3.141592654... 25 Egypt and the Babylonians π = = 3.125 8 2  8 Rhind Papyrus 1650 BCE π = 4   = 3.16  9 223 22 Archimedes 278 -212 BCE <π < 71 7 Ptolemy 150 BCE π = 3.1416 π 1 1 1 Gregory 1638 - 1675 AD = 1- + - + .... 4 3 5 7 Look
up
the
websites
for
further
approxima^ons
of
Pi.
Why
shouldn’t
you
print
this? Can
you
figure
out
a
way
with
a
compass
and
ruler
to
draw
this
pajern.
Yours
does
not
have
to
be
the
same
size!
Someone
in
your
group
 can
colour
it
in
if
you
want.
Worksheet Three This
circle
is
divided
up
into
16
sectors.
Cut
along
the
lines.
Take
one
unshaded
sector
and
cut
it
into
two.
Place
the
7
unshaded
sectors
onto
of
the
 8
shaded
sectors.
Place
the
halves
on
either
side.

The
combined
shape
is
approximately
equal
to
the
area
of
a
rectangle.
 Half the circumference = πr Therefore we can see the area of this rectangle A=l×w r =π r × r =π r 2 The area of the circle would be the same!
Begin by giving your group a name! Be creative and This
is
a
challenge.
The
winning
team
wins
a
 imaginative! chance
at
breaking
the
record!
 We
will
assess
you
on: PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
 Presenta^on
and
Neatness organiser
you
will
use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. Working
Mathema^cally Working
Crea^vely 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? Problem
Solving 3.
What
assump^ons
do
you
need
to
make?
(How
big
is
the
average
person?
What
parts
of
the
car
can’t
you Interes^ng
Ideas 



use?
Will
clothes
make
a
difference?

Are
you
allowing
for
space
in
between
people? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
(PMI) TASKS 1.
Read
Who
Sank
the
Boat
by
Pamela
Allen
and
illustrate
it
as
a
 QUESTIONS 



cartoon.

You
can
also
watch
the
YouTube
video 



Who
Sank
the
Boat 1.
What
is
the
best
way
to
determine
how
much
space
there
is
in
a
car? 2.
Read
Archimedes
and
Boats
and
design
your
own
experiment
to
 2.
What
is
the
best
way
to
determine
the
volume
of
a
person? 



explain
displacement
theory. 3.
Explain
displacement
theory. 4.
Decide
how
you
will
sit
and
lie
in
the
car
and
work
out
how
many
people
you
will
need. 5.
Work
out
a
strategy
to
put
people
in
the
car
as
you
will
be
^med. 6.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Habits of Mind you will need to complete this project: Thinking Flexibly Thinking Creatively Thinking Critically Persistence Responsible Risk Taking Managing your Impulsivity Group Effectiveness
This
is
a
challenge.
The
winning
team
wins
a
chance
at
breaking
the
record!
 We
will
assess
you
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
on
 a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
use,
e.g.
a
spider
web,
a
 list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
What
assump^ons
do
you
need
to
make?
(How
big
is
the
average
person?
What
parts
of
the
car
can’t
you 



use?
Will
clothes
make
a
difference?

Are
you
allowing
for
space
in
between
people? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
(PMI) Step Four The
project
is
divided
up
into
tasks,
ques^ons
and
worksheets.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
 each
of
them.


Step Five TASKS 1.
Read
Who
Sank
the
Boat
by
Pamela
Allen
and
illustrate
it
as
a
cartoon.

You
can
also
watch
the
YouTube
video

Who
Sank
the
Boat 2.
Read
Archimedes
and
Boats
and
design
your
own
experiment
to
explain
displacement
theory. Step Six QUESTIONS 1.
What
is
the
best
way
to
determine
how
much
space
there
is
in
a
car?
 2.
Work
out
how
much
space
there
is
in
a
vintage
Fiat. 3.
Es^mate
the
capacity
of
air
in
a
small
car? 4.
What
is
the
best
way
to
determine
the
volume
of
a
person? 5.
Explain
displacement
theory. 6.
Decide
how
you
will
sit
and
lie
in
the
car
and
work
out
how
many
people
you
will
need. 7.
Work
out
a
strategy
to
put
people
in
the
car
as
you
will
be
^med. 8.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
This
is
a
challenge.
The
winning
team
wins
a
chance
at
breaking
the
record!
 We
will
assess
you
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
 on
a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
use,
e.g.
a
spider
web,
a
 list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
What
assump^ons
do
you
need
to
make?
(How
big
is
the
average
person?
What
parts
of
the
car
can’t
you 



use?
Will
clothes
make
a
difference?

Are
you
allowing
for
space
in
between
people? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
(PMI) Step Four The
project
is
divided
up
into
tasks,
ques^ons
and
worksheets.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
 each
of
them.


Step Five TASKS 1.
Read
Who
Sank
the
Boat
by
Pamela
Allen
and
illustrate
it
as
a
cartoon.

You
can
also
watch
the
YouTube
video

Who
Sank
the
Boat 2.
Read
Archimedes
and
Boats
and
design
your
own
experiment
to
explain
displacement
theory. Step Six QUESTIONS 1.
What
is
the
best
way
to
determine
how
much
space
there
is
in
a
car?
 2.
Work
out
how
much
space
there
is
in
a
vintage
Fiat. 3.
Es^mate
the
capacity
of
air
in
a
small
car? 4.
What
is
the
best
way
to
determine
the
volume
of
a
person? 5.
Explain
displacement
theory. 6.
Decide
how
you
will
sit
and
lie
in
the
car
and
work
out
how
many
people
you
will
need. 7.
Work
out
a
strategy
to
put
people
in
the
car
as
you
will
be
^med. 8.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
Worksheet
One 1.
Inves^gate
the
legal
requirements
for
calcula^ng
the
number
of
people
who
can
fit
into
a
public
hall
or
entertainment
centre,
i.e.
the




 




minimum
amount
of
air
per
person. 2.
What
is
the
length
of
a
side
of
a
cube
whose
volume
is
the
same
as
that
of
a
box,
18cm
long,
12cm
wide
and
8cm
high? 3.
Given
the
area
of
3
faces
of
this
rectangular
prism,
find
the
volume
of
the
prism. 
 42cm2 2 24cm 28cm 2 Puzzle The
water
level
in
the
following
cylinder
is
shown
on
the
lel.
Fill
in
the
water
level in
the
cylinder
which
has
been
^lted. 40cm The
Fish
Tank B A
fish
tank,
filled
with
water,
is
100
cm
long,
60cm
wide
 and
40
cm
high.
The
tank
is
^lted,
res^ng
on
a
60cm
 D edge,
with
the
water
level
reaching
C.
The
midpoint
of
 C AB.
Find
the
depth
of
water
in
the
fish
tank
once
AB
is
 100cm returned
to
its
horizontal
posi^on. A
Key
Concepts
about
Floa^ng
and
Sinking Whether
something
floats
depends
on
the
material
it
is
made
of,
not
its
weight. Objects
float
if
they
are
light
for
their
size
and
sink
if
they
are
heavy
for
their
size. An
object
can
be
light
for
its
size
if
it
contains
air,
such
as
a
hollow
ball. materials
with
a
boat
shape
will
float
because
they
effec^vely
contain
air. Water
pushes
up
on
objects
with
an
upthrust
force. Objects
float
if
the
upthrust
force
from
the
water
can
balance
their
weight
(gravity
force) Object
float
depending
on
their
density
compared
to
water;
for
an
object
to
float
its
density
needs
to
be
less
than
that
of
water. Objects
float
when
air
is
enclosed
in
an
object’
their
density
is
lowered
thereby
increasing
the
likelihood
of
floa^ng. The
upthrust
depends
on
the
amount
of
water
displaced. Objets
float
bejer
in
salty
water
(density
of
salt
water
is
greater
than
that
of
pure
water). Water
surfaces
have
a
cohesive
force
(surface
tension)
that
makes
them
act
like
a
skin. Small,
dense
objects
(e.g.
a
pin,
a
water
‐
spider)
can
float
on
the
surface
of
water
without
breaking
it
,
due
to
surface
tension
effects. Archimedes
Principle A
floa^ng
object
will
experience
an
upthrust
force
from
water,
equal
to
the
weight
of
water
displaced
(pushed
aside).
It
will
sink
into

 the
water
un^l
it
reaches
the
point
where
the
weight
of
the
water
pushed
aside
equals
its
won
weight.
For
an
object
that
is
floa^ng,
 the
mass
of
the
material
equals
the
mass
of
water
that
is
displaced
by
the
object
(1
kg
=
1L
of
water).
Dense
objects
cannot
displace
 enough
water
to
provide
an
upthrust
force
to
counterbalance
their
weight,
so
they
plummet
below
the
surface.
Objects
made
of
 material
denser
than
water
(e.g.
a
boat
made
of
iron)
can
s^ll
float
if
they
contain
air
so
that
the
mean
density
is
less
than
that
of
 water.
Archimedes
Can Key
Idea An
object
will
push
aside
an
amount
of
water
equal
to
its
volume.
The
upthrust
from
water
is
related
to
the
amount
of
water
displaced. You
will
need: an
empty
milk
carton a
drinking
straw scissors water s^cky
tape
or
Blu‐Tack a
small
measuring
cylinder
or
jar
with
level
markings plas^cine An
archimedes
Can
measures
the
amount
of
water
pushed
aside
by
objects
when
they
float
or
sink.
 S^ck
a
short
straw
into
the
top
of
an
empty
milk
carton
to
make
a
spout
and
seal
it
with
tape
or
blue
‐
tack.

 Fill
it
with
water
to
the
point
where
no
more
water
runs
out
of
the
spout.
Place
a
narrow
jar
or
measuring
cylinder
underneath
the
spout
to
catch
the
 water.
 Take
a
lump
of
plas^cine
the
size
of
a
ping
pong
ball
and
drop
it
carefully
into
the
can.
 Measure
the
amount
of
water
that
overflows.
This
is
the
volume
of
the
plas^cine. Set
up
the
can
again,
removing
the
water
from
the
jar,
and
squeeze
the
plas^cine
into
a
flat
shape.
Predict
what
will
happen
if
you
drop
the
plas^cine
 into
the
can.
 Now
shape
the
plas^cine
into
a
boat
that
will
float
in
the
can.
 Set
the
can
up
once
again
and
predict
how
much
water
will
be
pushed
aside
by
the
floa^ng
boat.
Can
you
explain
your
result? Explanatory
note:
The
plas^cine
has
the
same
volume
whether
it
is
round
or
flat,
so
that
first
two
results
should
be
the
same.
The
same
amount
of
water
 is
pushed
aside
by
the
same
amount
of
plas^cine.

The
boat,
however,
pushes
aside
much
more
water.

The
reason
is
that
the
air
enclosed
by
the
boat
is
 also
displacing
water,
and
so
more
water
is
pushed
out.
This
extra
water
pushed
aside
means
that
the
upthrust
force
is
much
greater
on
the
plas^cine
 (Archimedes’
Principle)
and
it
will
float.
It
is
enclosed
within
the
boat
shape,
therefore,
that
causes
the
boat
to
float.
Show Me You (and the universe and an atom) You are between one metre and two metres tall. You are made up of cells which range in size between 5 and 40 micrometres. A micrometer is 0.000 001 metres. (Can you write this in cm?) That’s the size you started at. Cells are made up of atoms which are about 0.000 000 000 1 metre across. That’s not very big. How many atoms, approximately would you have in you? Atoms are nearly all empty space. The nucleus, the middle bit, is only one thousandth of the size of an atom although it is almost all the mass. Elementary particles are smaller - they make up the nucleus.
Show Me You (and the universe and an atom) The inside of an atom called the nucleus (is only one hundredth Our class thousandths of an atom - but most of its weight) Our school The Jewish Community The Australian Community Cells - there are approximately 50 trillion cells in your body Cells make up tissues which make up the organs in our body
Show Me You (and the universe and an atom) Vaucluse to Queens Park 7km Earth to the Moon 380 000 km Earth to Sun 150 000 000km Sydney to Melbourne 900km Circumference of the earth 40 000km Supernova 170 000 light years away Andromeda galaxy 2.2 million light years away
The aim is to present yourself relative to something tiny and This
is
a
challenge.
The
winning
team
wins
a
 something large. wonderful
prize!
 We
will
assess
you
on: Begin by giving your group a name! Be creative and imaginative! Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely PLANNING
 Problem
Solving Interes^ng
Ideas You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
 organiser
you
will
use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? TASKS 3.
How
are
you
going
to
present
the
problem
(sculpture,
collage,
poster,
worksheet). 4.
You
might
like
to
use
another
logical
progression,
for
example.
popula^on
of
your
class,
city,
country
then
 1.
Illustrate
(as
a
drawing,
poster,
collage)
the
units
of
measurement 



world.

You
might
want
to
talk
about
the
amount
of
water
in
a
drop,
bath,
swimming
pool,
lake,
river,
cloud. 



of
length,
star^ng
with
km
and
ending
with
units
smaller
than
a
mm. 2.
Invent
a
new
nemonic
for
the
units
of
measurement
of
length.
(i.e. 



You
might
want
to
talk
about
distance
from
your
house
to
school,
to
Melbourne,
to
England,
around
the
 



King
Henry
Died
a
Miserable
Death
Called
Measles) 



world,
to
the
moon
etc. 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering? QUESTIONS Habits of Mind you will need to complete this project: 1.
What
is
a
google?
Write
this
in
scien^fic
nota^on. Thinking Flexibly Thinking Creatively 2.
Write
one
million,
one
billion,
one
trillion
in
scien^fic
nota^on. Thinking Critically 3.
What
is
a
nonometer
and
micrometer?
Write
them
in
terms
of
m.
Write
them
in
scien^fic
nota^on.
 Persistence 4.
How
do
you
write
very
small
numbers
in
scien^fic
nota^on. Responsible Risk Taking 5.
Research
what
numbers
greater
than
a
trillion
are
called. Managing your Impulsivity 6.
Design
a
group
portrait
(making
sure
you
use
the
idea
of
very
very
small
to
very
very
big!) Group Effectiveness 7.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them.
Problem The
aim
is
to
present
yourself
rela^ve
to
something
^ny
and
something
large. This
is
a
challenge.
The
winning
team
wins
a
great
prize!
 You
will
be
assessed
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
on
 a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
use,
e.g.
a
spider
web,
a
list,
 a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
How
are
you
going
to
present
the
problem
(sculpture,
collage,
poster,
worksheet). 4.
You
might
like
to
use
another
logical
progression,
for
example.
popula^on
of
your
class,
city,
country
then
 



world.

You
might
want
to
talk
about
the
amount
of
water
in
a
drop,
bath,
swimming
pool,
lake,
river,
cloud. 



You
might
want
to
talk
about
distance
from
your
house
to
school,
to
Melbourne,
to
England,
around
the
 



world,
to
the
moon
etc. 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
Step Four The
project
is
divided
up
into
tasks
and
ques^ons.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
each
of
 them.

 Step Five TASKS 1.
Illustrate
(as
a
drawing,
poster,
collage)
the
units
of
measurement
of
length,
star^ng
with
km
and
ending
with
units
smaller
than
a
mm. 2.
Invent
a
new
nemonic
for
the
units
of
measurement
of
length.
(i.e.
King
Henry
Died
a
Miserable
Death
Called
Measles) Step Six QUESTIONS 1.
What
is
a
googol?
 2.
Write
one
million,
one
billion,
one
trillion. 3.
What
is
a
nonometer
and
micrometer?
Write
them
in
terms
of
m.
 4.
How
do
you
write
very
small
numbers
in
scien^fic
nota^on. 5.
Research
what
numbers
greater
than
a
trillion
are
called. 6.
Design
a
group
portrait
(making
sure
you
use
the
idea
of
very
very
small
to
very
very
big!) 7.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
Problem The
aim
is
to
present
yourself
rela^ve
to
something
^ny
and
something
large. This
is
a
challenge.
The
winning
team
wins
a
great
prize!
 You
will
be
assessed
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
on
 a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
use,
e.g.
a
spider
web,
a
list,
 a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
How
are
you
going
to
present
the
problem
(sculpture,
collage,
poster,
worksheet). 4.
You
might
like
to
use
another
logical
progression,
for
example.
popula^on
of
your
class,
city,
country
then
 



world.

You
might
want
to
talk
about
the
amount
of
water
in
a
drop,
bath,
swimming
pool,
lake,
river,
cloud. 



You
might
want
to
talk
about
distance
from
your
house
to
school,
to
Melbourne,
to
England,
around
the
 



world,
to
the
moon
etc. 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
Step Four The
project
is
divided
up
into
tasks
and
ques^ons.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
each
of
 them.

 Step Five TASKS 1.
Illustrate
(as
a
drawing,
poster,
collage)
the
units
of
measurement
of
length,
star^ng
with
km
and
ending
with
units
smaller
than
a
mm. 2.
Invent
a
new
nemonic
for
the
units
of
measurement
of
length.
(i.e.
King
Henry
Died
a
Miserable
Death
Called
Measles) Step Six QUESTIONS 1.
What
is
a
googol? 2.
Write
one
million,
one
billion,
one
trillion. 3.
What
is
a
nonometer
and
micrometer?
Write
them
in
terms
of
m.

 4.
How
do
you
write
very
small
numbers
in
scien^fic
nota^on. 5.
Research
what
numbers
greater
than
a
trillion
are
called. 6.
Design
a
group
portrait
(making
sure
you
use
the
idea
of
very
very
small
to
very
very
big!) 7.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
Worksheet
One A
million
is
wrijen
as
1
000
000. Inves^gate
and
answer
ONE
of
the
following
ques^ons: How
long
does
it
take
you
to
count
to
one
million
(assume
you
can
say
one
number
per
second)? How
far
back
is
a
million
days? How
high
is
a
pile
of
a
million
sheets
of
A4
sheets? How
far
is
one
million
kilometres? Arrange
the
following
numbers
in
ascending
order. 22 222, 2 22 , 22 2 
 Scien^fic
Nota^on Scien^fic
Nota^on
is
used
to
express
numbers
that
are
very
large
or
very
small
in
a
convenient
way.
Astronomers
use
very
large
numbers
to
 calculate
distances
to
the
stars
and
great
masses
of
objects
such
as
our
Sun.
Microbiologists
use
very
small
numbers
to
measure
the
size
of
viruses
 and
cells. The
number
is
wrijen
as
a
product
of
a
number
between
1
and
10,
and
a
power
of
10
(represen^ng
the
number
of
decimal
places
the
decimal
 point
has
been
shiled
from
its
original
posi^on
in
the
original
number). 360 000 000 = 3.6 × 10 8 256 000 = 2.56 × 10 5 M HTH TTH TH H T U t h th 10 6 10 5 10 4 10 3 10 2 101 10 0 10 −1 10 −2 10 −3 Write
these
as
a
basic
numeral Write
these
in
scien^fic
nota^on 7.23 × 10 4 350 000 6.5 × 10 3 4 100 000 8.9 × 10 0 0.42 1.9 × 10 −1 0.32
Worksheet
Two Complete
the
table. 21 22 23 24 25 26 Note
the
pajern
for
the
last
digit
and
hence
find
the
last
digit
for
 27 212 215 What
would
you
accept
and
why?
 Your
parents
have
promised
you
pocket
money.
They
will
either
pay
you
$5
a
week
for
a
year
or
1c
for
the
first
week,
2c
for
the
second
week,
4c
for
the
 third
week
etc.
(They
will
double
the
amount
every
week).
Explain
your
decision
clearly.
 Puzzle Cells
in
your
body
double
every
minute.
At
4.00pm
Jim
measured
on
a
slide
approximately
2
600
000
cells.
When
would
there
have
been
half
the
number
of
 cells? Fermat’s
Last
Theorem Fermat’s
Last
Theorem
states
that
there
are
no
integer
solu^ons
to
the
equa^on
 a n + b n = c n for n > 2 Fermat
(1601
‐
65)
claimed
to
have
a
marvellous
proof
which
he
hinted
at
in
the
margin
of
his
book.
For
the
next
350
years
 mathema^cians
tried
in
vain
to
find
a
proof,
un^l
succeeding
in
recent
^mes.
Along
the
way
they
discovered
and
found
links
 between
different
branches
of
mathema^cs. Fermat
was
born
into
a
wealthy
French
family
and
became
a
lawyer
and
government
official
in
Toulouse.
Fermat
corresponded
 with
Descartes,
Pascal
and
Mersenne
and
worked
on
number
theory,
spirals
and
op^cs.
Self Portrait
Self Portrait
Me, The Universe and an Atom - A Self Portrait

More Related Content

PPTX
Pi101
byMyk96
 
PPTX
Pi Day 2013
byjschiele
 
PPTX
Pi tastic
byBetsy Kinnear
 
PPTX
Interesections presentation
bySameer Shah
 
PDF
Project planning form
byltilem
 
PDF
Project planning form
byltilem
 
PDF
Ab ed2009
byATSIMA
 
DOC
Mass Unit Plan
byJoe McClung
 
Pi101
byMyk96
 
Pi Day 2013
byjschiele
 
Pi tastic
byBetsy Kinnear
 
Interesections presentation
bySameer Shah
 
Project planning form
byltilem
 
Project planning form
byltilem
 
Ab ed2009
byATSIMA
 
Mass Unit Plan
byJoe McClung
 

Similar to Pi day final version

PDF
Time management march 10
byRaha International School
 
PPT
Di jan 28th
byGarette Tebay
 
PPTX
Ppt swoops, whoops, and loopde loops
bydenniscummings
 
PDF
U Learn O8f Pres
bycankiwi4
 
PDF
Your big play_experiment
byazzy_slider
 
PPTX
Webquest
byanm54
 
PPTX
Webquest
byanm54
 
PDF
Technical Competency And My Disposition Towards Mathematics
byDiane Allen
 
PPTX
Extreme Classroom Makeover Gifted Edition
byBrian Housand
 
PDF
Scottish Curriculum for Excellence Numeracy Outcomes
byLearning and Teaching Scotland
 
DOCX
Aaron Q1 PLP 2012_2013
byapowers1
 
DOC
Project planning forms faboulouslyhealthy
byDavidCraft
 
PDF
Home link 6.11
byackerkri
 
PDF
Homework Weeks 9 and 10
byTakahe One
 
PDF
Easter Island Harrison Orsbourne
byTakahe One
 
DOC
Fitness Fair PBL_0210revised
byEric Davolt
 
PDF
proceedings
byMaria Diamantopoulou
 
PDF
Characteristics of Gifted Children - Faster, Earlier, Differently
byGiftedkids.ie
 
PPSX
Behold the Turtle
byJames Nottingham
 
DOC
Phase 1 Local Standards for Career Competencies and Performance Indicators
byDr Peter Carey
 
Time management march 10
byRaha International School
 
Di jan 28th
byGarette Tebay
 
Ppt swoops, whoops, and loopde loops
bydenniscummings
 
U Learn O8f Pres
bycankiwi4
 
Your big play_experiment
byazzy_slider
 
Webquest
byanm54
 
Webquest
byanm54
 
Technical Competency And My Disposition Towards Mathematics
byDiane Allen
 
Extreme Classroom Makeover Gifted Edition
byBrian Housand
 
Scottish Curriculum for Excellence Numeracy Outcomes
byLearning and Teaching Scotland
 
Aaron Q1 PLP 2012_2013
byapowers1
 
Project planning forms faboulouslyhealthy
byDavidCraft
 
Home link 6.11
byackerkri
 
Homework Weeks 9 and 10
byTakahe One
 
Easter Island Harrison Orsbourne
byTakahe One
 
Fitness Fair PBL_0210revised
byEric Davolt
 
proceedings
byMaria Diamantopoulou
 
Characteristics of Gifted Children - Faster, Earlier, Differently
byGiftedkids.ie
 
Behold the Turtle
byJames Nottingham
 
Phase 1 Local Standards for Career Competencies and Performance Indicators
byDr Peter Carey
 

Recently uploaded

PDF
IMANI Africa files RTI request seeking full disclosure on 2026 SIM registrati...
bynservice241
 
PPTX
Semester 6 unit 2 Atopic dermatitis.pptx
bysachin7989
 
PDF
FAMILY ASSESSMENT FORMAT - CHN practical
byDr. Sudhadevi Sadanandan
 
PPTX
How to use search_read method in Odoo 18
byCeline George
 
PPTX
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
DOCX
Mobile applications Devlopment ReTest year 2025-2026
byDr. Mazin Mohamed alkathiri
 
PDF
NAVIGATE PHARMACY CAREER OPPORTUNITIES.pdf
byMd. Zakaria Faruki
 
PPTX
How to Manage Package Reservation in Odoo 18 Inventory
byCeline George
 
PPTX
ELEMENTS OF COMMUNICATION (UNIT 2) .pptx
byPOOJA KARVANDE
 
PPTX
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
PPTX
Details of Epithelial and Connective Tissue.pptx
byAshish Umale
 
PPTX
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PPTX
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
PDF
Analyzing the data of your initial survey
byThelma Villaflores
 
PDF
Current Electricity for first year physiotherapy
byGanesh Jadhav
 
PPTX
Searching in PubMed andCochrane_Practical Presentation.pptx
bySystematic Reviews Network (SRN)
 
PPTX
ATTENTION -PART 2.pptx Shilpa Hotakar for I semester BSc students
bySHILPA HOTAKAR
 
PPTX
York "Collaboration for Research Support at U-M Library"
byNational Information Standards Organization (NISO)
 
PPTX
Pig- piggy bank in Big Data Analytics.ppt.pptx
byVarshini M
 
PPTX
Cost of Capital - Cost of Equity, Cost of debenture, Cost of Preference share...
bySundar B N
 
IMANI Africa files RTI request seeking full disclosure on 2026 SIM registrati...
bynservice241
 
Semester 6 unit 2 Atopic dermatitis.pptx
bysachin7989
 
FAMILY ASSESSMENT FORMAT - CHN practical
byDr. Sudhadevi Sadanandan
 
How to use search_read method in Odoo 18
byCeline George
 
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
Mobile applications Devlopment ReTest year 2025-2026
byDr. Mazin Mohamed alkathiri
 
NAVIGATE PHARMACY CAREER OPPORTUNITIES.pdf
byMd. Zakaria Faruki
 
How to Manage Package Reservation in Odoo 18 Inventory
byCeline George
 
ELEMENTS OF COMMUNICATION (UNIT 2) .pptx
byPOOJA KARVANDE
 
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
Details of Epithelial and Connective Tissue.pptx
byAshish Umale
 
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
Analyzing the data of your initial survey
byThelma Villaflores
 
Current Electricity for first year physiotherapy
byGanesh Jadhav
 
Searching in PubMed andCochrane_Practical Presentation.pptx
bySystematic Reviews Network (SRN)
 
ATTENTION -PART 2.pptx Shilpa Hotakar for I semester BSc students
bySHILPA HOTAKAR
 
York "Collaboration for Research Support at U-M Library"
byNational Information Standards Organization (NISO)
 
Pig- piggy bank in Big Data Analytics.ppt.pptx
byVarshini M
 
Cost of Capital - Cost of Equity, Cost of debenture, Cost of Preference share...
bySundar B N
 

Pi day final version

  • 1.
  • 2.
  • 3.
  • 4.
  • 6.
  • 7.
    Cou ntdo matical Idol! wn! Mathe Qu izdo m!
  • 8.
    Year 6, 7and 8 will be doing a project on MEASUREMENT. You will be introduced to the project in the Middle School Meeting Room during your first maths lesson of the week. You will then be put into groups of 4. Each maths lesson you will go to your regular classroom and complete the project. There will be a maths riddle in Hayom every day of this week. There will be a COUNTDOWN competition for all of the Middle School during lunch on Tuesday. There will be a QUIZDOM competition during lunch on Wednesday. There will be a MATHEMATICAL IDOL during lunch on Thursday. Cou ntdo matical Idol! wn! Mathe Qu izdo m!
  • 10.
    This is noordinary Maths Week! The prizes are spectacular! spectacular The prize will not only be awarded to the best group in each year but also to the children who have participated the most enthusiastically! Year 7 “Clowning Around!” Year 6 “You, Me, An Atom and the Universe” Year 8 “Mmmm Pizza Party”
  • 11.
  • 13.
    This
is
a
challenge.
The
winning
team
wins
a
 30cm 40cm 50cm pizza!
 You
will
be
assessed
on: Presenta^on
and
Neatness Medium
$8 Large
$10 Family
$16 Working
Mathema^cally Begin by giving your group a name! Be creative and imaginative! Working
Crea^vely Problem
Solving Interes^ng
Ideas PLANNING You
need
to
brainstorm
this
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
 organiser
you
will
use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. TASKS 1.
What
do
you
need
to
know
before
you
begin? 1.
Cut
out
20
people
from
magazines
and
newspapers
to
represent
 




the
people
at
your
party.
(You
must
use
a
range
of
ages).
Display


 
 2.
What
do
you
need
to
do
to
solve
this
problem? 




them
neatly
in
a
poster. 3.
What
assump^ons
do
you
need
to
make? 2.
Each
group
will
be
given
a
recipe.
You
need
to
arrange
the
recipe 4.
What
do
you
predict
you
will
find? 



in
the
correct
sequence. 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering? QUESTIONS Habits of Mind you will need to complete this project: Thinking Flexibly 1.
What
is
the
area
of
each
of
the
pizzas?
(Round
to
two
decimal
places) Thinking Creatively 2.
What
is
the
circumference
of
each
of
the
pizzas?
(Round
to
two
decimal
places) Thinking Critically 3.
What
is
the
cost
per
cm
square? Persistence ο ο 4.
What
is
the
cost
of
a
slice
of
pizza
which
is
18


and
320




? Responsible Risk Taking Managing your Impulsivity 5.
How
much
would
one
slice
of
pizza
cost?
(Decide
how
many
slices
the
pizzas
should
be
cut
into.) Group Effectiveness 6.
Which
is
the
best
value? 7.
Looking
at
the
party
guests,
decide
how
much
pizza
each
person
would
eat?
Give
reasons
why? 8.
How
many
pizzas
should
Mrs
Apfelbaum
be
ordering
and
what
sizes? 9.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them.
  • 14.
    30cm 40cm 50cm Medium
$8 Large
$10 Family
$16 This
is
a
challenge.
The
winning
team
wins
a
pizza!
 You
will
be
assessed
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
  • 15.
    Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
 on
a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING You
need
to
brainstorm
this
problem
and
add
how
you
thought
about
this
project
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
 use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
What
assump^ons
do
you
need
to
make? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering? Step Four The
project
is
divided
up
into
tasks,
ques^ons
and
worksheets.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
 each
of
them.


  • 16.
    Step Five TASKS
(Choose
at
least
2
of
them) 1.
Decide
on
the
20
people
who
are
invited
to
your
party.
(You
can
even
add
some
famous
people!)
Cut
out
20
people
from
magazines
to
represent 




your
guests.
You
MUST
use
a
range
of
ages
(as
shown
in
the
keynote).
Display
them
as
crea^vely
as
you
like
in
a
poster,
collage
or
assemblage. 


 2.
Each
group
will
be
given
a
recipe
on
how
to
make
a
pizza.
You
need
to
arrange
the
recipe
into
sequen^al
order
and
paste
it
onto
a
piece
of
paper. 3.
Design
a
name
and
menu
for
a
new
pizza
place
around
the
corner! 



 Step Six QUESTIONS
(Answer
all
of
these
ques^ons) 1.
What
is
the
area
of
each
of
the
pizzas?
(Round
to
two
decimal
places) 2.
What
is
the
circumference
of
each
of
the
pizzas?
(Round
to
two
decimal
places) 3.
What
is
the
cost
per
cm
square? 4.
If
the
family
size
pizza
is
cut
into
8
slices,
how
many
square
cm
would
that
be
and
how
much
would
each
slice
cost? 5.
If
the
medium
and
large
pizza
is
cut
into
8
slices,
how
many
square
cm
would
that
be
and
how
much
would
each
slice
cost? 6.
Which
is
the
best
value? 7.
Looking
at
the
party
guests,
decide
how
much
pizza
each
person
would
eat?
Give
reasons
why?
(Be
crea^ve
with
your
answers) 8.
How
many
pizzas
should
Mrs
Apfelbaum
be
ordering
and
what
sizes? 9.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
  • 17.
    30cm 40cm 50cm Medium
$8 Large
$10 Family
$16 This
is
a
challenge.
The
winning
team
wins
a
pizza!
 You
will
be
assessed
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
  • 18.
    Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
 on
a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING You
need
to
brainstorm
this
problem
and
add
how
you
thought
about
this
project
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
 use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
What
assump^ons
do
you
need
to
make? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering? Step Four The
project
is
divided
up
into
tasks,
ques^ons
and
worksheets.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
 each
of
them.


  • 19.
    Step Five TASKS
(Choose
at
least
2
of
them) 1.
Decide
on
the
20
people
who
are
invited
to
your
party.
(You
can
even
add
some
famous
people!)
Cut
out
20
people
from
magazines
to
represent 




your
guests.
You
MUST
use
a
range
of
ages
(as
shown
in
the
keynote).
Display
them
as
crea^vely
as
you
like
in
a
poster,
collage
or
assemblage. 


 2.
Each
group
will
be
given
a
recipe
on
how
to
make
a
pizza.
You
need
to
arrange
the
recipe
into
sequen^al
order
and
paste
it
onto
a
piece
of
paper. 3.
Design
a
name
and
menu
for
a
new
pizza
place
around
the
corner! 



 Step Six QUESTIONS
(Answer
all
of
these
ques^ons) 1.
What
is
the
area
of
each
of
the
pizzas?
(Round
to
two
decimal
places) 2.
What
is
the
circumference
of
each
of
the
pizzas?
(Round
to
two
decimal
places) 3.
What
is
the
cost
per
cm
square? 4.
If
the
family
size
pizza
is
cut
into
8
slices,
how
many
square
cm
would
that
be
and
how
much
would
each
slice
cost? 5.
If
the
medium
and
large
pizza
is
cut
into
8
slices,
how
many
square
cm
would
that
be
and
how
much
would
each
slice
cost? 6.
Which
is
the
best
value? 7.
Looking
at
the
party
guests,
decide
how
much
pizza
each
person
would
eat?
Give
reasons
why?
(Be
crea^ve
with
your
answers) 8.
How
many
pizzas
should
Mrs
Apfelbaum
be
ordering
and
what
sizes? 9.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
  • 20.
    Worksheet One What
parts
of
the
circle
are
there
in
these
prac^cal
examples? Circumference The
circumference
is
a
special
name
we
give
to
the
perimeter
of
the
circle.
 Measure
and
cut
a
string
of
length
20
cm.
Take
the
string
and
form
a
circle
by
joining
its
two
ends.
Es^mate
how
much
longer
the
circumference
is
than
the
 diameter?

Now
measure
the
diameter.
Divide
20
cm
(the
circumference)
by
the
measurement
of
the
diameter. Now,
cut
the
string
into
a
length
of
15
cm.
Again
form
a
circle
and
measure
the
diameter.
Divide
15
cm
(the
circumference)
by
the
measurement
of
the
diameter. Now,
cut
the
string
into
a
length
of
10
cm.
Again
form
a
circle
and
measure
the
diameter.
Divide
10
cm
(the
circumference)
by
the
measurement
of
the
diameter. What
have
you
found
each
^me? Pi Our
inves^ga^ons
have
shown
that
the
circumference
of
a
circle
is
just
more
than
three
^mes
the
diameter.
The
ancient
Greeks,
Egyp^ans,
Chinese
and
others
 
 π knew
about
this
special
number.
A
special
Greek
lejer









(pronounced
Pi)
stands
for C ≈ 3.14 ≈ 3 1 d 7 A
regular
hexagon
with
sides
3
cm
is
circumscribed
by
a
circle
(a
circle
is
drawn
around
the
hexagon).
Diameters
are
 drawn
to
the
ver^ces
of
the
hexagon. How
many
triangles
have
been
drawn
and
what
kind
of
triangles
are
they? What
is
the
length
of
the
diameter
of
the
circle? What
is
the
perimeter
of
the
hexagon? Is
the
circumference
of
the
circle
slightly
longer
than
the
perimeter
of
the
hexagon? Therefore
what
can
you
conclude
about
the
length
of
the
circumference
in
rela^on
to
the
length
of
the
diameter?
  • 21.
    Worksheet Two Pi
has
a
long
history
and
the
following
is
a
short
list
of
approxima^ons
that
have
been
found
for
Pi.
The
calculator
has
Pi
as
3.141592654... 25 Egypt and the Babylonians π = = 3.125 8 2  8 Rhind Papyrus 1650 BCE π = 4   = 3.16  9 223 22 Archimedes 278 -212 BCE <π < 71 7 Ptolemy 150 BCE π = 3.1416 π 1 1 1 Gregory 1638 - 1675 AD = 1- + - + .... 4 3 5 7 Look
up
the
websites
for
further
approxima^ons
of
Pi.
Why
shouldn’t
you
print
this? Can
you
figure
out
a
way
with
a
compass
and
ruler
to
draw
this
pajern.
Yours
does
not
have
to
be
the
same
size!
Someone
in
your
group
 can
colour
it
in
if
you
want.
  • 22.
    Worksheet Three This
circle
is
divided
up
into
16
sectors.
Cut
along
the
lines.
Take
one
unshaded
sector
and
cut
it
into
two.
Place
the
7
unshaded
sectors
onto
of
the
 8
shaded
sectors.
Place
the
halves
on
either
side.

The
combined
shape
is
approximately
equal
to
the
area
of
a
rectangle.
 Half the circumference = πr Therefore we can see the area of this rectangle A=l×w r =π r × r =π r 2 The area of the circle would be the same!
  • 24.
    Begin by givingyour group a name! Be creative and This
is
a
challenge.
The
winning
team
wins
a
 imaginative! chance
at
breaking
the
record!
 We
will
assess
you
on: PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
 Presenta^on
and
Neatness organiser
you
will
use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. Working
Mathema^cally Working
Crea^vely 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? Problem
Solving 3.
What
assump^ons
do
you
need
to
make?
(How
big
is
the
average
person?
What
parts
of
the
car
can’t
you Interes^ng
Ideas 



use?
Will
clothes
make
a
difference?

Are
you
allowing
for
space
in
between
people? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
(PMI) TASKS 1.
Read
Who
Sank
the
Boat
by
Pamela
Allen
and
illustrate
it
as
a
 QUESTIONS 



cartoon.

You
can
also
watch
the
YouTube
video 



Who
Sank
the
Boat 1.
What
is
the
best
way
to
determine
how
much
space
there
is
in
a
car? 2.
Read
Archimedes
and
Boats
and
design
your
own
experiment
to
 2.
What
is
the
best
way
to
determine
the
volume
of
a
person? 



explain
displacement
theory. 3.
Explain
displacement
theory. 4.
Decide
how
you
will
sit
and
lie
in
the
car
and
work
out
how
many
people
you
will
need. 5.
Work
out
a
strategy
to
put
people
in
the
car
as
you
will
be
^med. 6.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Habits of Mind you will need to complete this project: Thinking Flexibly Thinking Creatively Thinking Critically Persistence Responsible Risk Taking Managing your Impulsivity Group Effectiveness
  • 25.
    This
is
a
challenge.
The
winning
team
wins
a
chance
at
breaking
the
record!
 We
will
assess
you
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
  • 26.
    Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
on
 a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
use,
e.g.
a
spider
web,
a
 list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
What
assump^ons
do
you
need
to
make?
(How
big
is
the
average
person?
What
parts
of
the
car
can’t
you 



use?
Will
clothes
make
a
difference?

Are
you
allowing
for
space
in
between
people? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
(PMI) Step Four The
project
is
divided
up
into
tasks,
ques^ons
and
worksheets.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
 each
of
them.


  • 27.
    Step Five TASKS 1.
Read
Who
Sank
the
Boat
by
Pamela
Allen
and
illustrate
it
as
a
cartoon.

You
can
also
watch
the
YouTube
video

Who
Sank
the
Boat 2.
Read
Archimedes
and
Boats
and
design
your
own
experiment
to
explain
displacement
theory. Step Six QUESTIONS 1.
What
is
the
best
way
to
determine
how
much
space
there
is
in
a
car?
 2.
Work
out
how
much
space
there
is
in
a
vintage
Fiat. 3.
Es^mate
the
capacity
of
air
in
a
small
car? 4.
What
is
the
best
way
to
determine
the
volume
of
a
person? 5.
Explain
displacement
theory. 6.
Decide
how
you
will
sit
and
lie
in
the
car
and
work
out
how
many
people
you
will
need. 7.
Work
out
a
strategy
to
put
people
in
the
car
as
you
will
be
^med. 8.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
  • 28.
    This
is
a
challenge.
The
winning
team
wins
a
chance
at
breaking
the
record!
 We
will
assess
you
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
  • 29.
    Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
 on
a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
use,
e.g.
a
spider
web,
a
 list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
What
assump^ons
do
you
need
to
make?
(How
big
is
the
average
person?
What
parts
of
the
car
can’t
you 



use?
Will
clothes
make
a
difference?

Are
you
allowing
for
space
in
between
people? 4.
What
do
you
predict
you
will
find? 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
(PMI) Step Four The
project
is
divided
up
into
tasks,
ques^ons
and
worksheets.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
 each
of
them.


  • 30.
    Step Five TASKS 1.
Read
Who
Sank
the
Boat
by
Pamela
Allen
and
illustrate
it
as
a
cartoon.

You
can
also
watch
the
YouTube
video

Who
Sank
the
Boat 2.
Read
Archimedes
and
Boats
and
design
your
own
experiment
to
explain
displacement
theory. Step Six QUESTIONS 1.
What
is
the
best
way
to
determine
how
much
space
there
is
in
a
car?
 2.
Work
out
how
much
space
there
is
in
a
vintage
Fiat. 3.
Es^mate
the
capacity
of
air
in
a
small
car? 4.
What
is
the
best
way
to
determine
the
volume
of
a
person? 5.
Explain
displacement
theory. 6.
Decide
how
you
will
sit
and
lie
in
the
car
and
work
out
how
many
people
you
will
need. 7.
Work
out
a
strategy
to
put
people
in
the
car
as
you
will
be
^med. 8.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
  • 31.
    Worksheet
One 1.
Inves^gate
the
legal
requirements
for
calcula^ng
the
number
of
people
who
can
fit
into
a
public
hall
or
entertainment
centre,
i.e.
the




 




minimum
amount
of
air
per
person. 2.
What
is
the
length
of
a
side
of
a
cube
whose
volume
is
the
same
as
that
of
a
box,
18cm
long,
12cm
wide
and
8cm
high? 3.
Given
the
area
of
3
faces
of
this
rectangular
prism,
find
the
volume
of
the
prism. 
 42cm2 2 24cm 28cm 2 Puzzle The
water
level
in
the
following
cylinder
is
shown
on
the
lel.
Fill
in
the
water
level in
the
cylinder
which
has
been
^lted. 40cm The
Fish
Tank B A
fish
tank,
filled
with
water,
is
100
cm
long,
60cm
wide
 and
40
cm
high.
The
tank
is
^lted,
res^ng
on
a
60cm
 D edge,
with
the
water
level
reaching
C.
The
midpoint
of
 C AB.
Find
the
depth
of
water
in
the
fish
tank
once
AB
is
 100cm returned
to
its
horizontal
posi^on. A
  • 32.
    Key
Concepts
about
Floa^ng
and
Sinking Whether
something
floats
depends
on
the
material
it
is
made
of,
not
its
weight. Objects
float
if
they
are
light
for
their
size
and
sink
if
they
are
heavy
for
their
size. An
object
can
be
light
for
its
size
if
it
contains
air,
such
as
a
hollow
ball. materials
with
a
boat
shape
will
float
because
they
effec^vely
contain
air. Water
pushes
up
on
objects
with
an
upthrust
force. Objects
float
if
the
upthrust
force
from
the
water
can
balance
their
weight
(gravity
force) Object
float
depending
on
their
density
compared
to
water;
for
an
object
to
float
its
density
needs
to
be
less
than
that
of
water. Objects
float
when
air
is
enclosed
in
an
object’
their
density
is
lowered
thereby
increasing
the
likelihood
of
floa^ng. The
upthrust
depends
on
the
amount
of
water
displaced. Objets
float
bejer
in
salty
water
(density
of
salt
water
is
greater
than
that
of
pure
water). Water
surfaces
have
a
cohesive
force
(surface
tension)
that
makes
them
act
like
a
skin. Small,
dense
objects
(e.g.
a
pin,
a
water
‐
spider)
can
float
on
the
surface
of
water
without
breaking
it
,
due
to
surface
tension
effects. Archimedes
Principle A
floa^ng
object
will
experience
an
upthrust
force
from
water,
equal
to
the
weight
of
water
displaced
(pushed
aside).
It
will
sink
into

 the
water
un^l
it
reaches
the
point
where
the
weight
of
the
water
pushed
aside
equals
its
won
weight.
For
an
object
that
is
floa^ng,
 the
mass
of
the
material
equals
the
mass
of
water
that
is
displaced
by
the
object
(1
kg
=
1L
of
water).
Dense
objects
cannot
displace
 enough
water
to
provide
an
upthrust
force
to
counterbalance
their
weight,
so
they
plummet
below
the
surface.
Objects
made
of
 material
denser
than
water
(e.g.
a
boat
made
of
iron)
can
s^ll
float
if
they
contain
air
so
that
the
mean
density
is
less
than
that
of
 water.
  • 33.
    Archimedes
Can Key
Idea An
object
will
push
aside
an
amount
of
water
equal
to
its
volume.
The
upthrust
from
water
is
related
to
the
amount
of
water
displaced. You
will
need: an
empty
milk
carton a
drinking
straw scissors water s^cky
tape
or
Blu‐Tack a
small
measuring
cylinder
or
jar
with
level
markings plas^cine An
archimedes
Can
measures
the
amount
of
water
pushed
aside
by
objects
when
they
float
or
sink.
 S^ck
a
short
straw
into
the
top
of
an
empty
milk
carton
to
make
a
spout
and
seal
it
with
tape
or
blue
‐
tack.

 Fill
it
with
water
to
the
point
where
no
more
water
runs
out
of
the
spout.
Place
a
narrow
jar
or
measuring
cylinder
underneath
the
spout
to
catch
the
 water.
 Take
a
lump
of
plas^cine
the
size
of
a
ping
pong
ball
and
drop
it
carefully
into
the
can.
 Measure
the
amount
of
water
that
overflows.
This
is
the
volume
of
the
plas^cine. Set
up
the
can
again,
removing
the
water
from
the
jar,
and
squeeze
the
plas^cine
into
a
flat
shape.
Predict
what
will
happen
if
you
drop
the
plas^cine
 into
the
can.
 Now
shape
the
plas^cine
into
a
boat
that
will
float
in
the
can.
 Set
the
can
up
once
again
and
predict
how
much
water
will
be
pushed
aside
by
the
floa^ng
boat.
Can
you
explain
your
result? Explanatory
note:
The
plas^cine
has
the
same
volume
whether
it
is
round
or
flat,
so
that
first
two
results
should
be
the
same.
The
same
amount
of
water
 is
pushed
aside
by
the
same
amount
of
plas^cine.

The
boat,
however,
pushes
aside
much
more
water.

The
reason
is
that
the
air
enclosed
by
the
boat
is
 also
displacing
water,
and
so
more
water
is
pushed
out.
This
extra
water
pushed
aside
means
that
the
upthrust
force
is
much
greater
on
the
plas^cine
 (Archimedes’
Principle)
and
it
will
float.
It
is
enclosed
within
the
boat
shape,
therefore,
that
causes
the
boat
to
float.
  • 34.
    Show Me You (and the universe and an atom) You are between one metre and two metres tall. You are made up of cells which range in size between 5 and 40 micrometres. A micrometer is 0.000 001 metres. (Can you write this in cm?) That’s the size you started at. Cells are made up of atoms which are about 0.000 000 000 1 metre across. That’s not very big. How many atoms, approximately would you have in you? Atoms are nearly all empty space. The nucleus, the middle bit, is only one thousandth of the size of an atom although it is almost all the mass. Elementary particles are smaller - they make up the nucleus.
  • 35.
    Show Me You (and the universe and an atom) The inside of an atom called the nucleus (is only one hundredth Our class thousandths of an atom - but most of its weight) Our school The Jewish Community The Australian Community Cells - there are approximately 50 trillion cells in your body Cells make up tissues which make up the organs in our body
  • 36.
    Show Me You (and the universe and an atom) Vaucluse to Queens Park 7km Earth to the Moon 380 000 km Earth to Sun 150 000 000km Sydney to Melbourne 900km Circumference of the earth 40 000km Supernova 170 000 light years away Andromeda galaxy 2.2 million light years away
  • 37.
    The aim isto present yourself relative to something tiny and This
is
a
challenge.
The
winning
team
wins
a
 something large. wonderful
prize!
 We
will
assess
you
on: Begin by giving your group a name! Be creative and imaginative! Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely PLANNING
 Problem
Solving Interes^ng
Ideas You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
 organiser
you
will
use,
e.g.
a
spider
web,
a
list,
a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? TASKS 3.
How
are
you
going
to
present
the
problem
(sculpture,
collage,
poster,
worksheet). 4.
You
might
like
to
use
another
logical
progression,
for
example.
popula^on
of
your
class,
city,
country
then
 1.
Illustrate
(as
a
drawing,
poster,
collage)
the
units
of
measurement 



world.

You
might
want
to
talk
about
the
amount
of
water
in
a
drop,
bath,
swimming
pool,
lake,
river,
cloud. 



of
length,
star^ng
with
km
and
ending
with
units
smaller
than
a
mm. 2.
Invent
a
new
nemonic
for
the
units
of
measurement
of
length.
(i.e. 



You
might
want
to
talk
about
distance
from
your
house
to
school,
to
Melbourne,
to
England,
around
the
 



King
Henry
Died
a
Miserable
Death
Called
Measles) 



world,
to
the
moon
etc. 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering? QUESTIONS Habits of Mind you will need to complete this project: 1.
What
is
a
google?
Write
this
in
scien^fic
nota^on. Thinking Flexibly Thinking Creatively 2.
Write
one
million,
one
billion,
one
trillion
in
scien^fic
nota^on. Thinking Critically 3.
What
is
a
nonometer
and
micrometer?
Write
them
in
terms
of
m.
Write
them
in
scien^fic
nota^on.
 Persistence 4.
How
do
you
write
very
small
numbers
in
scien^fic
nota^on. Responsible Risk Taking 5.
Research
what
numbers
greater
than
a
trillion
are
called. Managing your Impulsivity 6.
Design
a
group
portrait
(making
sure
you
use
the
idea
of
very
very
small
to
very
very
big!) Group Effectiveness 7.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them.
  • 38.
    Problem The
aim
is
to
present
yourself
rela^ve
to
something
^ny
and
something
large. This
is
a
challenge.
The
winning
team
wins
a
great
prize!
 You
will
be
assessed
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
  • 39.
    Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
on
 a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
use,
e.g.
a
spider
web,
a
list,
 a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
How
are
you
going
to
present
the
problem
(sculpture,
collage,
poster,
worksheet). 4.
You
might
like
to
use
another
logical
progression,
for
example.
popula^on
of
your
class,
city,
country
then
 



world.

You
might
want
to
talk
about
the
amount
of
water
in
a
drop,
bath,
swimming
pool,
lake,
river,
cloud. 



You
might
want
to
talk
about
distance
from
your
house
to
school,
to
Melbourne,
to
England,
around
the
 



world,
to
the
moon
etc. 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
  • 40.
    Step Four The
project
is
divided
up
into
tasks
and
ques^ons.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
each
of
 them.

 Step Five TASKS 1.
Illustrate
(as
a
drawing,
poster,
collage)
the
units
of
measurement
of
length,
star^ng
with
km
and
ending
with
units
smaller
than
a
mm. 2.
Invent
a
new
nemonic
for
the
units
of
measurement
of
length.
(i.e.
King
Henry
Died
a
Miserable
Death
Called
Measles) Step Six QUESTIONS 1.
What
is
a
googol?
 2.
Write
one
million,
one
billion,
one
trillion. 3.
What
is
a
nonometer
and
micrometer?
Write
them
in
terms
of
m.
 4.
How
do
you
write
very
small
numbers
in
scien^fic
nota^on. 5.
Research
what
numbers
greater
than
a
trillion
are
called. 6.
Design
a
group
portrait
(making
sure
you
use
the
idea
of
very
very
small
to
very
very
big!) 7.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
  • 41.
    Problem The
aim
is
to
present
yourself
rela^ve
to
something
^ny
and
something
large. This
is
a
challenge.
The
winning
team
wins
a
great
prize!
 You
will
be
assessed
on: Presenta^on
and
Neatness Working
Mathema^cally Working
Crea^vely Problem
Solving Interes^ng
Ideas Step One Begin by giving your group a name! Be creative and imaginative!
  • 42.
    Step Two Discuss
the
habits
of
mind
that
you
will
need
to
complete
this
project.
List
them
in
order
from
most
important
to
least
important.
Write
this
up
neatly
on
 a
piece
of
paper.
There
is
no
right
or
wrong
answer. Thinking
Flexibly Thinking
Crea^vely Thinking
Cri^cally
(Logically) Persistence Responsible
Risk
Taking Managing
your
Impulsivity Group
Effec^veness Step Three PLANNING
 You
need
to
brainstorm
the
problem
and
add
your
thinking
to
your
final
product.
Decide
on
which
graphic
organiser
you
will
use,
e.g.
a
spider
web,
a
list,
 a
venn
diagram
etc. 1.
What
do
you
need
to
know
before
you
begin?
How
can
you
find
out
this
informa^on? 2.
What
do
you
need
to
do
to
solve
this
problem? 3.
How
are
you
going
to
present
the
problem
(sculpture,
collage,
poster,
worksheet). 4.
You
might
like
to
use
another
logical
progression,
for
example.
popula^on
of
your
class,
city,
country
then
 



world.

You
might
want
to
talk
about
the
amount
of
water
in
a
drop,
bath,
swimming
pool,
lake,
river,
cloud. 



You
might
want
to
talk
about
distance
from
your
house
to
school,
to
Melbourne,
to
England,
around
the
 



world,
to
the
moon
etc. 5.
What
other
interes^ng/posi^ve/nega^ve
things
should
you
be
considering?
  • 43.
    Step Four The
project
is
divided
up
into
tasks
and
ques^ons.

Read
them
all
first
and
then
divide
these
up
and
decide
who
is
best
suited
to
complete
each
of
 them.

 Step Five TASKS 1.
Illustrate
(as
a
drawing,
poster,
collage)
the
units
of
measurement
of
length,
star^ng
with
km
and
ending
with
units
smaller
than
a
mm. 2.
Invent
a
new
nemonic
for
the
units
of
measurement
of
length.
(i.e.
King
Henry
Died
a
Miserable
Death
Called
Measles) Step Six QUESTIONS 1.
What
is
a
googol? 2.
Write
one
million,
one
billion,
one
trillion. 3.
What
is
a
nonometer
and
micrometer?
Write
them
in
terms
of
m.

 4.
How
do
you
write
very
small
numbers
in
scien^fic
nota^on. 5.
Research
what
numbers
greater
than
a
trillion
are
called. 6.
Design
a
group
portrait
(making
sure
you
use
the
idea
of
very
very
small
to
very
very
big!) 7.
On
reflec^on,
name
3
habits
of
mind
that
you
used
and
how
you
used
them. Step Seven Complete
the
worksheets
given
to
your
group.
  • 44.
    Worksheet
One A
million
is
wrijen
as
1
000
000. Inves^gate
and
answer
ONE
of
the
following
ques^ons: How
long
does
it
take
you
to
count
to
one
million
(assume
you
can
say
one
number
per
second)? How
far
back
is
a
million
days? How
high
is
a
pile
of
a
million
sheets
of
A4
sheets? How
far
is
one
million
kilometres? Arrange
the
following
numbers
in
ascending
order. 22 222, 2 22 , 22 2 
 Scien^fic
Nota^on Scien^fic
Nota^on
is
used
to
express
numbers
that
are
very
large
or
very
small
in
a
convenient
way.
Astronomers
use
very
large
numbers
to
 calculate
distances
to
the
stars
and
great
masses
of
objects
such
as
our
Sun.
Microbiologists
use
very
small
numbers
to
measure
the
size
of
viruses
 and
cells. The
number
is
wrijen
as
a
product
of
a
number
between
1
and
10,
and
a
power
of
10
(represen^ng
the
number
of
decimal
places
the
decimal
 point
has
been
shiled
from
its
original
posi^on
in
the
original
number). 360 000 000 = 3.6 × 10 8 256 000 = 2.56 × 10 5 M HTH TTH TH H T U t h th 10 6 10 5 10 4 10 3 10 2 101 10 0 10 −1 10 −2 10 −3 Write
these
as
a
basic
numeral Write
these
in
scien^fic
nota^on 7.23 × 10 4 350 000 6.5 × 10 3 4 100 000 8.9 × 10 0 0.42 1.9 × 10 −1 0.32
  • 45.
    Worksheet
Two Complete
the
table. 21 22 23 24 25 26 Note
the
pajern
for
the
last
digit
and
hence
find
the
last
digit
for
 27 212 215 What
would
you
accept
and
why?
 Your
parents
have
promised
you
pocket
money.
They
will
either
pay
you
$5
a
week
for
a
year
or
1c
for
the
first
week,
2c
for
the
second
week,
4c
for
the
 third
week
etc.
(They
will
double
the
amount
every
week).
Explain
your
decision
clearly.
 Puzzle Cells
in
your
body
double
every
minute.
At
4.00pm
Jim
measured
on
a
slide
approximately
2
600
000
cells.
When
would
there
have
been
half
the
number
of
 cells? Fermat’s
Last
Theorem Fermat’s
Last
Theorem
states
that
there
are
no
integer
solu^ons
to
the
equa^on
 a n + b n = c n for n > 2 Fermat
(1601
‐
65)
claimed
to
have
a
marvellous
proof
which
he
hinted
at
in
the
margin
of
his
book.
For
the
next
350
years
 mathema^cians
tried
in
vain
to
find
a
proof,
un^l
succeeding
in
recent
^mes.
Along
the
way
they
discovered
and
found
links
 between
different
branches
of
mathema^cs. Fermat
was
born
into
a
wealthy
French
family
and
became
a
lawyer
and
government
official
in
Toulouse.
Fermat
corresponded
 with
Descartes,
Pascal
and
Mersenne
and
worked
on
number
theory,
spirals
and
op^cs.
  • 46.
  • 47.
  • 48.
    Me, The Universeand an Atom - A Self Portrait

Editor's Notes