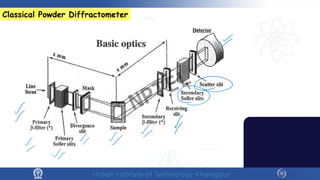
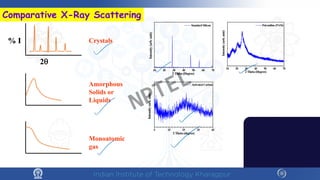
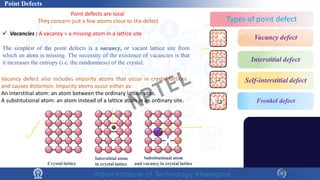
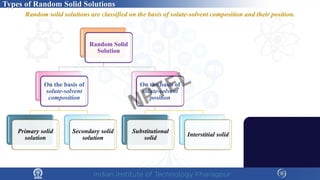
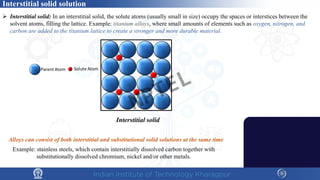
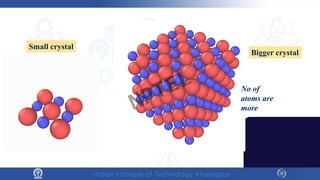
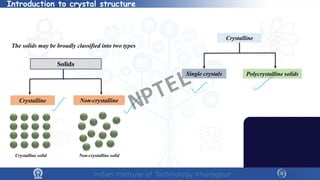
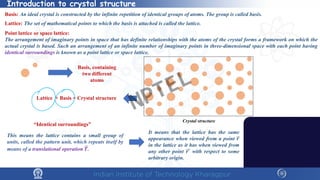
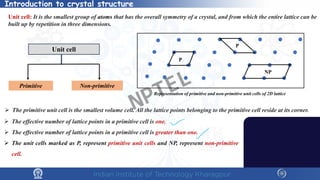
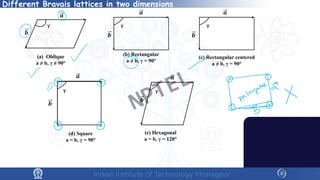
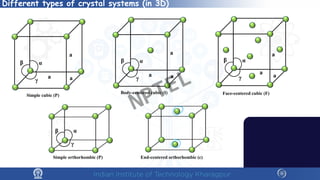
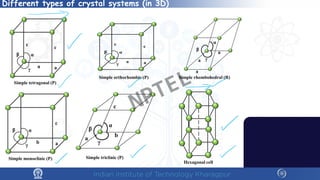
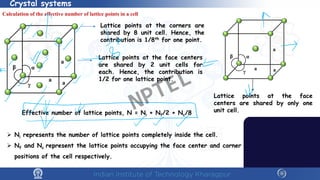
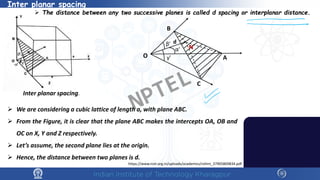
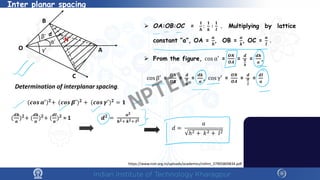
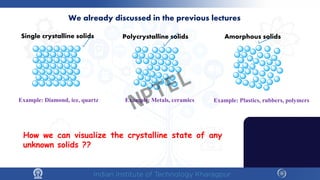
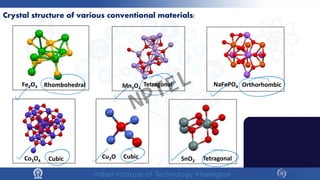
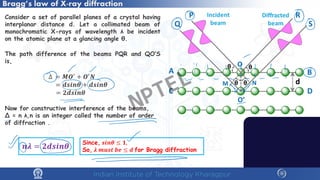
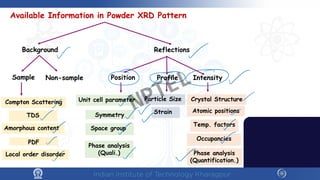
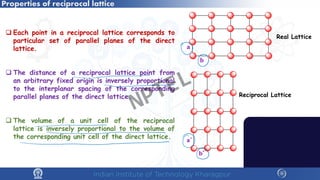
The document covers the synthesis protocols and crystal structures of materials, focusing on different types of lattices, unit cells, and crystal systems, including bravais lattices. It explains concepts like miller indices, inter-planar spacing, and x-ray diffraction for analyzing crystal structures. The lecture emphasizes the significance of symmetries within crystal structures and introduces techniques for visualizing crystalline states using x-ray diffraction methods.

1. Physics of Functional Materials & Devices
Prof. Amreesh Chandra
Department of Physics, IIT KHARAGPUR
Module 02: Synthesis protocols and crystal structures of materials
Lecture 10 : Crystal structure - II
NPTEL

2.  Types of lattices
 Crystal structures and types
 Miller indices
NPTEL

3. In the previous week, we discussed the following concepts…
NPTEL

4. Atom
1 D Lattice
2 D Lattice
a
NPTEL

5. Small crystal
Bigger crystal
No of
atoms are
more
NPTEL

6. Introduction to crystal structure
Solids
Crystalline Non-crystalline
The solids may be broadly classified into two types
Crystalline solid Non-crystalline solid
Single crystals
Crystalline
Polycrystalline solids
NPTEL

7. Introduction to crystal structure
Basis: An ideal crystal is constructed by the infinite repetition of identical groups of atoms. The group is called basis.
Lattice: The set of mathematical points to which the basis is attached is called the lattice.
Point lattice or space lattice:
The arrangement of imaginary points in space that has definite relationships with the atoms of the crystal forms a framework on which the
actual crystal is based. Such an arrangement of an infinite number of imaginary points in three-dimensional space with each point having
identical surroundings is known as a point lattice or space lattice.
Lattice + Basis = Crystal structure
Basis, containing
two different
atoms
Crystal structure
“Identical surroundings”
It means that the lattice has the same
appearance when viewed from a point 𝒓𝒓
in the lattice as it has when viewed from
any other point 𝒓𝒓′ with respect to some
arbitrary origin.
This means the lattice contains a small group of
units, called the pattern unit, which repeats itself by
means of a translational operation 𝑻𝑻.
NPTEL

8. Unit cell: It is the smallest group of atoms that has the overall symmetry of a crystal, and from which the entire lattice can be
built up by repetition in three dimensions.
Unit cell
Primitive Non-primitive
Representation of primitive and non-primitive unit cells of 2D lattice
P
NP
P
 The primitive unit cell is the smallest volume cell. All the lattice points belonging to the primitive cell reside at its corner.
 The effective number of lattice points in a primitive cell is one.
 The effective number of lattice points in a primitive cell is greater than one.
 The unit cells marked as P, represent primitive unit cells and NP, represent non-primitive
cell.
Introduction to crystal structure
NPTEL

9. Any type of crystal structure always satisfies the symmetry operation.
Then we discussed the symmetry operations
NPTEL

10. Let us now understand more about the crystal structures and
their importance.
NPTEL

11. Different types of lattices
 Crystal lattices can be carried or mapped into themselves by the lattice translations T and by various other symmetry
operations.
 According to that 2D and 3D lattices can be classified into four and seven crystal systems, respectively.
 There are 14 Bravais lattices in 3D, grouped in seven crystal systems, and 5 Bravais lattices in 2D, grouped in four
crystal systems.
What is a Bravais lattice?
Bravais lattice is the lattice in which the atom or all the atoms at lattice points are identical or if the surroundings of
each lattice point are the same.
Bravais in 1948 showed that 14 lattices are sufficient to describe all crystals.
These 14 lattices are known as Bravais lattices.
NPTEL

12. Crystal systems in two dimensions
Crystal systems and Bravais lattices in two dimensions
Serial No. Crystal system Bravais lattice Conventional
unit cell
Unit cell
characteristics
1 Oblique Oblique Parallelogram a ≠ b, γ ≠ 90°
2 Rectangular 1. Rectangular primitive
2. Rectangular centered
Rectangle a ≠ b, γ = 90°
3 Square Square Square a = b, γ = 90°
4 Hexagonal Hexagonal 60° Rhombus a = b, γ = 120°
 The rectangular crystal system has two Bravais lattices, namely, rectangular
primitive and rectangular centered.
 In all, there are five Bravais lattices in two dimensions.
NPTEL

13. 𝒂𝒂
𝒃𝒃
γ
(a) Oblique
a ≠ b, γ ≠ 90°
(b) Rectangular
a ≠ b, γ = 90°
𝒂𝒂
𝒃𝒃
(c) Rectangular centered
a ≠ b, γ = 90°
𝒂𝒂
𝒃𝒃
𝒂𝒂
𝒃𝒃
(d) Square
a = b, γ = 90°
γ
𝒂𝒂
𝒃𝒃
(e) Hexagonal
a = b, γ = 120°
γ
γ γ
Different Bravais lattices in two dimensions
NPTEL

14. Crystal systems and Bravais lattice in three dimensions
Serial
No.
Crystal system Lattice parameters Bravais lattice Lattice
symbol
Examples
1 Cubic a=b=c
α = β = γ = 90°
Simple
Body centered
Face centered
P
I
F
Cu, Ag, Fe,
Na, NaCl,
CsCl, etc.
2 Tetragonal a=b ≠ c
α = β = γ = 90°
Simple
Body centered
P
I
β-Sn,
TiO2.
3 Orthorhombic a ≠ b ≠ c
α = β = γ = 90°
Simple
Body centered
End centered
Face centered
P
I
C
F
Ga,
Fe3C
(cementite)
4 Rhombohedral
or Trigonal
a=b=c
α = β = γ ≠ 90°
Simple P As, Sb, Bi
5 Hexagonal a=b ≠ c
α = β =90°, γ = 120°
Simple P Mg, Zn, Cd, NiAs
6 Monoclinic a ≠ b ≠ c
α = γ = 90° ≠ β
Simple
End centered
P
F
CaSO4. 2H2O
(gypsum)
7 Triclinic a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90°
Simple P K2Cr2O7
NPTEL

15. Different types of crystal systems (in 3D)
α
β
γ
a
a
a
α
β
γ
a
a
a
Simple cubic (P)
Body-centered cubic (I)
α
β
γ
a
a
a
Face-centered cubic (F)
End-centered orthorhombic (c)
α
β
γ
Simple orthorhombic (P)
NPTEL

16. Different types of crystal systems (in 3D)
Simple tetragonal (P)
Simple orthorhombic (P)
a
b
c
α
β
γ
Simple triclinic (P)
Simple rhombohedral (R)
Simple monoclinic (P)
Hexagonal cell
NPTEL

17. Crystal systems
Calculation of the effective number of lattice points in a cell
α
β
γ
a
a
a
Lattice points at the corners are
shared by 8 unit cell. Hence, the
contribution is 1/8th for one point.
Lattice points at the face centers
are shared by 2 unit cells for
each. Hence, the contribution is
1/2 for one lattice point.
Lattice points at the face
centers are shared by only one
unit cell.
Effective number of lattice points, N = Ni + Nf/2 + Nc/8
 Ni represents the number of lattice points completely inside the cell.
 Nf and Nc represent the lattice points occupying the face center and corner
positions of the cell respectively.
NPTEL

18. Lattice directions and planes
Plane designation by Miller indices.
 The orientation of planes in a lattice is symbolically represented
by the English crystallographer Miller. The indices of a plane
are therefore known as the Miller indices.
 In crystallography, we use Miller indices to specify locations, directions,
and planes in a crystal.
The steps involved to determine the Miller indices of a plane
are:
 Find the intercepts of the plane on the crystallographic axes.
 Take the reciprocal of these intercepts.
 Simplify to remove fractions, if any, and enclose the numbers
obtained into parentheses.
Miller indices of a plane are in general written as (hkl).
NPTEL

19. Lattice directions and planes
Axial lengths 4 8 3
Intercept lengths 2 6 3
Fractional intercepts 1/2 3/4 1
Miller indices
2
6
4/3
4
1
3
Example of determining Millar indices
1Å 2Å 3Å 4Å
2Å
1Å
c
0
3Å
8Å
(643)
b
a
Plane designation by Miller indices.
 If a plane intercepts an axis on the negative side, a bar is put above the
corresponding number of Miller indices, for example: (𝟎𝟎�
𝟏𝟏𝟎𝟎).
 If a plane passes through the origin, then in general another plane parallel
to it is taken to determine Millar indices.
 Millar indices of all the parallel planes are the same.
NPTEL

20. Inter planar spacing
https://www.rcet.org.in/uploads/academics/rohini_37905869834.pdf
Inter planar spacing.
 The distance between any two successive planes is called d spacing or interplanar distance.
α'
β'
γ'
O A
B
C
d
N
 We are considering a cubic lattice of length a, with plane ABC.
 From the Figure, it is clear that the plane ABC makes the intercepts OA, OB and
OC on X, Y and Z respectively.
 Let’s assume, the second plane lies at the origin.
 Hence, the distance between two planes is d.
NPTEL

21. Inter planar spacing
https://www.rcet.org.in/uploads/academics/rohini_37905869834.pdf
 OA:OB:OC =
𝟏𝟏
𝒉𝒉
:
𝟏𝟏
𝒌𝒌
∶
𝟏𝟏
𝒍𝒍
. Multiplying by lattice
constant “a”, OA =
𝒂𝒂
𝒉𝒉
, OB =
𝒂𝒂
𝒌𝒌
, OC =
𝒂𝒂
𝒍𝒍
.
 From the figure, cos α′ =
𝑶𝑶𝑶𝑶
𝑶𝑶𝑶𝑶
=
𝒅𝒅
𝒂𝒂
𝒉𝒉
=
𝒅𝒅𝒅𝒅
𝒂𝒂
,
cos β′ =
𝑶𝑶𝑶𝑶
𝑶𝑶𝑩𝑩
=
𝒅𝒅
𝒂𝒂
𝒌𝒌
=
𝒅𝒅𝒌𝒌
𝒂𝒂
, cos γ′ =
𝑶𝑶𝑶𝑶
𝑶𝑶𝑶𝑶
=
𝒅𝒅
𝒂𝒂
𝒍𝒍
=
𝒅𝒅𝒍𝒍
𝒂𝒂
α'
β'
γ'
O A
B
C
d
N
Determination of interplanar spacing.
(𝒄𝒄𝒄𝒄𝒄𝒄 𝜶𝜶′)𝟐𝟐
+ (𝒄𝒄𝒄𝒄𝒄𝒄 𝜷𝜷′)𝟐𝟐
+ (𝒄𝒄𝒄𝒄𝒄𝒄 𝜸𝜸′)𝟐𝟐
= 𝟏𝟏
(
𝒅𝒅𝒅𝒅
𝒂𝒂
)𝟐𝟐+ (
𝒅𝒅𝒅𝒅
𝒂𝒂
)𝟐𝟐+ (
𝒅𝒅𝒅𝒅
𝒂𝒂
)𝟐𝟐 = 1 𝒅𝒅𝟐𝟐 =
𝒂𝒂𝟐𝟐
𝒉𝒉𝟐𝟐+ 𝒌𝒌𝟐𝟐+ 𝒍𝒍𝟐𝟐
𝑑𝑑 =
𝑎𝑎
ℎ2 + 𝑘𝑘2 + 𝑙𝑙2
NPTEL

22. In Miller indices, the brackets and commas matter a lot!
Notation Representation
(h,k,l) Point
[hkl] Direction
<hkl> Family of directions
(hkl) Plane
{hkl} Family of planes
Negative weights can be represented with a bar over the relevant number
NPTEL

23. The concepts of lattice, basis, and unit cells are described.
Different types of crystal symmetry operations are described.
Basic concepts of Bravais lattice, point groups, and space groups are highlighted.
7 crystal systems in 3D lattices are discussed.
The concept of Miller indices and lattices planes are highlighted.
NPTEL

24.  Solid State Physics by R.K. Puri and V.K. Babbar.
 Physics of Functional Materials by Hasse Fredriksson and Ula Akerlind.
 Introduction to Solid State Physics by Charles Kittel.
 Solid State Physics by Ashcroft and Mermin.
NPTEL

25. Thank you…
NPTEL

26. Physics of Functional Materials & Devices
Prof. Amreesh Chandra
Department of Physics, IIT KHARAGPUR
Module 02: Synthesis protocols and crystal structures of materials
Lecture 11 : Crystal structure and X-ray Diffraction
NPTEL

27.  X-ray diffraction
 Reciprocal lattice
 Geometric structure factor
NPTEL

28. We already discussed in the previous lectures
Single crystalline solids Polycrystalline solids Amorphous solids
Example: Diamond, ice, quartz Example: Metals, ceramics Example: Plastics, rubbers, polymers
How we can visualize the crystalline state of any
unknown solids ??
NPTEL

29. Mn3O4
Crystal structure of various conventional materials:
Co3O4 Cubic
Tetragonal
SnO2 Tetragonal
Cu2O Cubic
NaFePO4 Orthorhombic
Fe2O3 Rhombohedral
NPTEL

30. How we can visualize the arrangements of atoms or
molecules in any unknown materials?
NPTEL

31. We can visualize the crystalline state of any unknown solids by X-ray
diffraction method
What is diffraction?
 Diffraction is the interference or bending of waves around
the corners of an obstacle or through an aperture into the
region of geometrical shadow of the obstacle/aperture.
 The diffraction pattern consisted by the series of dark
spots arranged in a definite order on a photographic film.
 So, X-ray diffraction technique is an important tool to
determine the crystalline state and crystal structure of
the materials.
Diffraction
A diffraction pattern of a red laser beam
projected onto a plate after passing through
a small circular aperture in another plate
https://en.wikipedia.org/wiki/Diffraction
NPTEL

32.  The atoms in a single crystal are regularly
arranged with interatomic spacing of the order of
a few angstroms, which act as a three-
dimensional natural grating for X-rays.
 This phenomena is first suggested by the German
physicist Max Von Laue in 1912.
 Friedrich & Knipping successfully demonstrated
the diffraction of X-rays from a thin single
crystal of zinc blend (ZnS).
X-ray diffraction from Crystal:
X-ray diffraction (XRD)
NPTEL

33. Condition of X-ray diffraction
Diffraction Condition from lattice
 Since, atomic spacings are of the order of an angstrom, the useful wavelength range
will lie in the region of 0.1 to 10 Å.
𝝀𝝀 ≤ 𝒅𝒅
where ‘𝝀𝝀’ is the wavelength of the incident radiation & ‘d’ is the lattice constant of the
material.
Will a diffraction pattern be visible when optical
light will incident on the crystal?
(The theorem will be discussed in the
upcoming slides)
NPTEL

34. Why X-Ray is generally used for diffraction?
Optical wavelength: λ ≅ 𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒 𝒕𝒕𝒕𝒕 𝟕𝟕𝟕𝟕𝟕𝟕𝟕𝟕 Å
Ordinary optical reflection will be take place.
𝑰𝑰𝑰𝑰 𝒕𝒕𝒕𝒕𝒕𝒕𝒕𝒕 𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄, 𝝀𝝀 ≫ 𝒅𝒅, 𝒘𝒘𝒘𝒘𝒘𝒘𝒘𝒘𝒘𝒘 𝒅𝒅 ≅ 𝟏𝟏 Å
NPTEL

35. 𝒏𝒏𝝀𝝀 = 𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝜽𝜽
Bragg’s law of X-Ray diffraction
The Nobel Prize in Physics 1915 was awarded jointly to Sir William
Henry Bragg and William Lawrence Bragg for their study and analysis of
crystal structure by means of X-rays."
The Nobel Prize in Physics 1915
Bragg’s Law
𝑺𝑺𝑺𝑺, 𝝀𝝀 ≤ 𝒅𝒅
𝑨𝑨𝑨𝑨, 𝒔𝒔𝒔𝒔𝒔𝒔𝒔 ≤ 𝟏𝟏
NPTEL

36. Bragg’s law of X-ray diffraction
Consider a set of parallel planes of a crystal having
interplanar distance d. Let a collimated beam of
monochromatic X-rays of wavelength λ be incident
on the atomic plane at a glancing angle θ.
The path difference of the beams PQR and QO’S
is,
∆ = 𝑴𝑴𝑶𝑶′ + 𝑶𝑶′𝑵𝑵
= 𝒅𝒅𝒅𝒅𝒅𝒅𝒅𝒅𝜽𝜽 + 𝒅𝒅𝒅𝒅𝒅𝒅𝒅𝒅𝜽𝜽
= 𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝜽𝜽
Now for constructive interference of the beams,
∆ = n λ,n is an integer called the number of order
of diffraction .
Since, 𝒔𝒔𝒔𝒔𝒔𝒔𝜽𝜽 ≤ 𝟏𝟏,
So, 𝝀𝝀 𝒎𝒎𝒎𝒎𝒎𝒎𝒎𝒎 𝒃𝒃𝒃𝒃 ≤ 𝒅𝒅 for Bragg diffraction
𝒏𝒏𝝀𝝀 = 𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝜽𝜽
NPTEL

37. X-Ray powder diffraction method
 X-ray powder diffraction (XRD) is a rapid analytical
technique, used for phase identification of a crystalline
material.
 This is most widely used diffraction method to determine the
structure of crystalline solids.
 The sample used in the form of a fine powder. Each particle
of the powder is a tiny crystal oriented at random with
respect to the incident beam.
 Monochromatic X-rays (constant λ ) is used by passing the
X-rays through a filter.
 The diffraction take place for those values of d and θ which
satisfy the Bragg’s condition, i.e. 𝒏𝒏λ = 𝟐𝟐𝟐𝟐 𝑺𝑺𝑺𝑺𝑺𝑺𝑺.
NPTEL

38. Atomic positions
Available Information in Powder XRD Pattern
Background Reflections
Non-sample
Sample
Compton Scattering
TDS
Amorphous content
PDF
Local order disorder
Position Intensity
Profile
Unit cell parameter
Symmetry
Space group
Phase analysis
(Quali.)
Particle Size
Strain
Crystal Structure
Temp. factors
Occupancies
Phase analysis
(Quantification.)
NPTEL

39. Reciprocal lattice
 The diffraction of X-rays occurs from various sets of parallel planes having
different orientations and internal spacing.
 In certain situation involving the presence of a number of sets of parallel
planes with different orientation, it becomes difficult to visualize all such
planes.
The problem was simplified by P.P. Ewald by
developing a new type of lattice know as the
reciprocal lattice.
Direct lattice Reciprocal lattice
Problem in direct lattice:
NPTEL

40. Properties of reciprocal lattice
 Each point in a reciprocal lattice corresponds to
particular set of parallel planes of the direct
lattice.
 The distance of a reciprocal lattice point from
an arbitrary fixed origin is inversely proportional
to the interplanar spacing of the corresponding
parallel planes of the direct lattice.
 The volume of a unit cell of the reciprocal
lattice is inversely proportional to the volume of
the corresponding unit cell of the direct lattice.
Real Lattice
Reciprocal Lattice
NPTEL

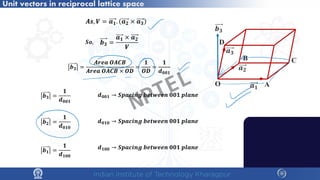
41. Unit vectors in reciprocal lattice space
Unit vectors in real space:
𝒂𝒂𝟏𝟏 𝒂𝒂𝟐𝟐 𝒂𝒂𝟑𝟑
Unit vectors in reciprocal lattice space:
𝒃𝒃𝟏𝟏 𝒃𝒃𝟐𝟐 𝒃𝒃𝟑𝟑
𝒃𝒃𝟏𝟏 =
𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑
𝒂𝒂𝟏𝟏. (𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑)
𝒃𝒃𝟐𝟐 =
𝒂𝒂𝟑𝟑 × 𝒂𝒂𝟏𝟏
𝒂𝒂𝟏𝟏. (𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑)
𝒃𝒃𝟑𝟑 =
𝒂𝒂𝟏𝟏 × 𝒂𝒂𝟐𝟐
𝒂𝒂𝟏𝟏. (𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑)
Unit vectors relation between real space and reciprocal lattice space :
𝒂𝒂𝟏𝟏. 𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑 = 𝑽𝑽, 𝒗𝒗𝒗𝒗𝒗𝒗𝒗𝒗𝒗𝒗𝒗𝒗 𝒐𝒐𝒐𝒐 𝒕𝒕𝒕𝒕𝒕𝒕 𝒖𝒖𝒖𝒖𝒖𝒖𝒖𝒖 𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄
𝒃𝒃𝟑𝟑 =
𝒂𝒂𝟏𝟏 × 𝒂𝒂𝟐𝟐
𝑽𝑽
𝑺𝑺𝑺𝑺, 𝒃𝒃𝟑𝟑 � 𝒂𝒂𝟐𝟐 = 𝟎𝟎
𝒃𝒃𝟑𝟑 � 𝒂𝒂𝟏𝟏 = 𝟎𝟎
𝒃𝒃𝟑𝟑 � 𝒂𝒂𝟑𝟑 = 𝟏𝟏
𝒃𝒃𝒊𝒊 � 𝒂𝒂𝒋𝒋 = 𝟎𝟎 [𝒊𝒊 ≠ 𝒋𝒋]
𝒃𝒃𝒊𝒊 � 𝒂𝒂𝒋𝒋 = 𝟏𝟏 [𝒊𝒊 = 𝒋𝒋]
𝒃𝒃𝟑𝟑 𝒊𝒊𝒊𝒊 𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑 𝒕𝒕𝒕𝒕 𝒂𝒂𝟏𝟏 × 𝒂𝒂𝟐𝟐 𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑
NPTEL

42. Unit vectors in reciprocal lattice space
𝒃𝒃𝟑𝟑 =
𝒂𝒂𝟏𝟏 × 𝒂𝒂𝟐𝟐
𝑽𝑽
𝑨𝑨𝑨𝑨, 𝑽𝑽 = 𝒂𝒂𝟏𝟏. 𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑
𝑺𝑺𝑺𝑺,
𝒃𝒃𝟑𝟑 =
𝑨𝑨𝑨𝑨𝑨𝑨𝑨𝑨 𝑶𝑶𝑶𝑶𝑶𝑶𝑶𝑶
𝑨𝑨𝑨𝑨𝑨𝑨𝑨𝑨 𝑶𝑶𝑶𝑶𝑶𝑶𝑶𝑶 × 𝑶𝑶𝑶𝑶
=
𝟏𝟏
𝑶𝑶𝑶𝑶
=
𝟏𝟏
𝒅𝒅𝟎𝟎𝟎𝟎𝟎𝟎
𝒃𝒃𝟑𝟑 =
𝟏𝟏
𝒅𝒅𝟎𝟎𝟎𝟎𝟎𝟎
𝒅𝒅𝟎𝟎𝟎𝟎𝟎𝟎 → 𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃 𝟎𝟎𝟎𝟎𝟎𝟎 𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑
𝒃𝒃𝟐𝟐 =
𝟏𝟏
𝒅𝒅𝟎𝟎𝟎𝟎𝟎𝟎
𝒃𝒃𝟏𝟏 =
𝟏𝟏
𝒅𝒅𝟏𝟏𝟏𝟏𝟏𝟏
𝒅𝒅𝟎𝟎𝟎𝟎𝟎𝟎 → 𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃 𝟎𝟎𝟎𝟎𝟎𝟎 𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑
𝒅𝒅𝟏𝟏𝟏𝟏𝟏𝟏 → 𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺𝑺 𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃𝒃 𝟎𝟎𝟎𝟎𝟎𝟎 𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑
NPTEL

43. Reciprocal lattice vector
𝑯𝑯𝒉𝒉𝒉𝒉𝒉𝒉 = 𝒉𝒉𝒃𝒃𝟏𝟏 + 𝒌𝒌𝒃𝒃𝟐𝟐 + 𝒍𝒍𝒃𝒃𝟑𝟑
• 𝑯𝑯𝒉𝒉𝒉𝒉𝒉𝒉 𝒊𝒊𝒊𝒊 𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑 𝒕𝒕𝒕𝒕 𝒕𝒕𝒕𝒕𝒕𝒕 𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑𝒑 𝒉𝒉𝒉𝒉𝒉𝒉
Two fundamental properties of reciprocal lattice vector:
• 𝑯𝑯𝒉𝒉𝒉𝒉𝒉𝒉 =
𝟏𝟏
𝒅𝒅𝒉𝒉𝒉𝒉𝒉𝒉
Reciprocal lattice vector for the plane with miller indices (hkl)
NPTEL

44. Reciprocal lattice to SCC lattice
The primitive translation vectors of a simple cubic lattice:
𝒂𝒂𝟏𝟏 = 𝒂𝒂 ̂
𝒊𝒊 𝒂𝒂𝟐𝟐 = 𝒂𝒂 ̂
𝒋𝒋 𝒂𝒂𝟑𝟑 = 𝒂𝒂 �
𝒌𝒌
Volume of simple cubic unit cell: 𝒂𝒂𝟏𝟏. 𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑 = 𝒂𝒂𝟑𝟑 ̂
𝒊𝒊. ̂
𝒋𝒋 × �
𝒌𝒌 = 𝒂𝒂𝟑𝟑
Reciprocal lattice vectors:
𝒃𝒃𝟏𝟏 =
𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑
𝒂𝒂𝟏𝟏. (𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑)
=
𝒂𝒂 ̂
𝒋𝒋 × 𝒂𝒂�
𝒌𝒌
𝒂𝒂𝟑𝟑 =
𝟏𝟏
𝒂𝒂
̂
𝒊𝒊
𝒃𝒃𝟐𝟐 =
𝒂𝒂𝟑𝟑 × 𝒂𝒂𝟏𝟏
𝒂𝒂𝟏𝟏. (𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑)
=
𝒂𝒂�
𝒌𝒌 × 𝒂𝒂 ̂
𝒊𝒊
𝒂𝒂𝟑𝟑
=
𝟏𝟏
𝒂𝒂
̂
𝒋𝒋
𝒃𝒃𝟑𝟑 =
𝒂𝒂𝟏𝟏 × 𝒂𝒂𝟐𝟐
𝒂𝒂𝟏𝟏. (𝒂𝒂𝟐𝟐 × 𝒂𝒂𝟑𝟑)
=
𝒂𝒂 ̂
𝒊𝒊 × 𝒂𝒂 ̂
𝒋𝒋
𝒂𝒂𝟑𝟑 =
𝟏𝟏
𝒂𝒂
�
𝒌𝒌
NPTEL

45. The reciprocal lattice to SC lattice is also simple cubic
but with lattice constant equal to
𝟏𝟏
𝒂𝒂
NPTEL

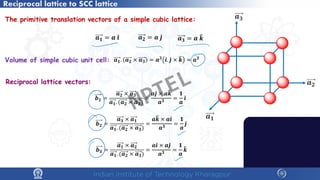
46. Reciprocal lattice to BCC lattice
The primitive translation vectors of a body-centred
cubic lattice:
𝒂𝒂′ =
𝒂𝒂
𝟐𝟐
( ̂
𝒊𝒊 + ̂
𝒋𝒋 − �
𝒌𝒌) 𝒃𝒃′
=
𝒂𝒂
𝟐𝟐
(− ̂
𝒊𝒊 + ̂
𝒋𝒋 + �
𝒌𝒌) 𝒄𝒄′
=
𝒂𝒂
𝟐𝟐
( ̂
𝒊𝒊 − ̂
𝒋𝒋 + �
𝒌𝒌)
The volume of the primitive cell : 𝑽𝑽 = 𝒂𝒂′
. (𝒃𝒃′ × 𝒄𝒄′)
=
𝒂𝒂
𝟐𝟐
̂
𝒊𝒊 + ̂
𝒋𝒋 − �
𝒌𝒌 . [
𝒂𝒂𝟐𝟐
𝟒𝟒
(− ̂
𝒊𝒊 + ̂
𝒋𝒋 + �
𝒌𝒌) × ( ̂
𝒊𝒊 − ̂
𝒋𝒋 + �
𝒌𝒌)]
=
𝒂𝒂
𝟐𝟐
̂
𝒊𝒊 + ̂
𝒋𝒋 − �
𝒌𝒌 .
𝒂𝒂𝟐𝟐
𝟐𝟐
( ̂
𝒊𝒊 + ̂
𝒋𝒋)
=
𝒂𝒂𝟑𝟑
𝟐𝟐
NPTEL

47. Reciprocal lattice vectors of BCC lattice:
𝒂𝒂∗ =
𝒃𝒃𝒃 × 𝒄𝒄′
𝒂𝒂′. 𝒃𝒃′ × 𝒄𝒄′
=
𝒂𝒂𝟐𝟐
𝟐𝟐
𝒂𝒂𝟑𝟑
𝟐𝟐
( ̂
𝒊𝒊 + ̂
𝒋𝒋) =
𝟏𝟏
𝒂𝒂
( ̂
𝒊𝒊 + ̂
𝒋𝒋)
𝒃𝒃∗
=
𝒄𝒄𝒄 × 𝒂𝒂′
𝒂𝒂′. 𝒃𝒃′ × 𝒄𝒄′
=
𝒂𝒂𝟐𝟐
𝟐𝟐
𝒂𝒂𝟑𝟑
𝟐𝟐
( ̂
𝒋𝒋 + �
𝒌𝒌) =
𝟏𝟏
𝒂𝒂
( ̂
𝒋𝒋 + �
𝒌𝒌)
𝒄𝒄∗ =
𝒂𝒂𝒂 × 𝒃𝒃′
𝒂𝒂′. 𝒃𝒃′ × 𝒄𝒄′
=
𝒂𝒂𝟐𝟐
𝟐𝟐
𝒂𝒂𝟑𝟑
𝟐𝟐
(�
𝒌𝒌 + ̂
𝒊𝒊) =
𝟏𝟏
𝒂𝒂
(�
𝒌𝒌 + ̂
𝒊𝒊)
Thus, the reciprocal lattice to a BCC lattice is FCC lattice
Reciprocal lattice to BCC lattice
NPTEL

48. Reciprocal lattice to FCC lattice
The primitive translation vectors of a face-centred cubic lattice:
𝒂𝒂′ =
𝒂𝒂
𝟐𝟐
( ̂
𝒊𝒊 + ̂
𝒋𝒋) 𝒃𝒃′
=
𝒂𝒂
𝟐𝟐
( ̂
𝒋𝒋 + �
𝒌𝒌) 𝒄𝒄′ =
𝒂𝒂
𝟐𝟐
(�
𝒌𝒌 + ̂
𝒊𝒊)
The volume of the primitive cell : 𝑽𝑽 = 𝒂𝒂′
. (𝒃𝒃′ × 𝒄𝒄′)
=
𝒂𝒂
𝟐𝟐
̂
𝒊𝒊 + ̂
𝒋𝒋 . [
𝒂𝒂𝟐𝟐
𝟒𝟒
( ̂
𝒋𝒋 + �
𝒌𝒌) × (�
𝒌𝒌 + ̂
𝒊𝒊)]
=
𝒂𝒂
𝟐𝟐
̂
𝒊𝒊 + ̂
𝒋𝒋 .
𝒂𝒂𝟐𝟐
𝟒𝟒
( ̂
𝒊𝒊 + ̂
𝒋𝒋 − �
𝒌𝒌)
=
𝒂𝒂𝟑𝟑
𝟒𝟒
NPTEL

49. Reciprocal lattice vectors of FCC lattice:
𝒂𝒂∗
=
𝒃𝒃𝒃 × 𝒄𝒄′
𝒂𝒂′. 𝒃𝒃′ × 𝒄𝒄′
=
𝒂𝒂𝟐𝟐
𝟒𝟒
( ̂
𝒊𝒊 + ̂
𝒋𝒋 − �
𝒌𝒌)
𝒂𝒂𝟑𝟑
𝟒𝟒
=
𝟏𝟏
𝒂𝒂
( ̂
𝒊𝒊 + ̂
𝒋𝒋 − �
𝒌𝒌)
𝒃𝒃∗ =
𝒄𝒄𝒄 × 𝒂𝒂′
𝒂𝒂′. 𝒃𝒃′ × 𝒄𝒄′
=
𝒂𝒂𝟐𝟐
𝟒𝟒
(− ̂
𝒊𝒊 + ̂
𝒋𝒋 + �
𝒌𝒌)
𝒂𝒂𝟑𝟑
𝟒𝟒
=
𝟏𝟏
𝒂𝒂
(− ̂
𝒊𝒊 + ̂
𝒋𝒋 + �
𝒌𝒌)
𝒄𝒄∗ =
𝒂𝒂𝒂 × 𝒃𝒃′
𝒂𝒂′. 𝒃𝒃′ × 𝒄𝒄′
=
𝒂𝒂𝟐𝟐
𝟒𝟒
( ̂
𝒊𝒊 − ̂
𝒋𝒋 + �
𝒌𝒌)
𝒂𝒂𝟑𝟑
𝟒𝟒
=
𝟏𝟏
𝒂𝒂
( ̂
𝒊𝒊 − ̂
𝒋𝒋 + �
𝒌𝒌)
Thus, the reciprocal lattice to a FCC lattice is BCC lattice
Reciprocal lattice to FCC lattice
NPTEL

50. Is the diffraction observed for all set of planes in
crystal structure??
Lets find out…
Before that, we have to know the expression of the
diffraction peak intensity.
NPTEL

51. The diffraction peak intensity
 The intensity (I) of diffraction peak from (h,k,l) plane depends of the Geometric structure
factor F hkl.
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 𝒆𝒆𝟐𝟐𝝅𝝅𝒊𝒊(𝒉𝒉𝒖𝒖𝒋𝒋+𝒌𝒌𝒗𝒗𝒋𝒋+𝒍𝒍𝒘𝒘𝒋𝒋)
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 =
𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂 𝒐𝒐𝒐𝒐 𝒕𝒕𝒕𝒕𝒕𝒕 𝒘𝒘𝒘𝒘𝒘𝒘𝒘𝒘 𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔 𝒃𝒃𝒃𝒃 𝒂𝒂𝒂𝒂𝒂𝒂 𝒕𝒕𝒕𝒕𝒕𝒕 𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂 𝒐𝒐𝒐𝒐 𝒂𝒂 𝒖𝒖𝒖𝒖𝒖𝒖𝒖𝒖 𝒄𝒄𝒄𝒄𝒄𝒄𝒄𝒄
𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂 𝒐𝒐𝒐𝒐 𝒕𝒕𝒕𝒕𝒕𝒕 𝒘𝒘𝒘𝒘𝒘𝒘𝒘𝒘 𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔 𝒃𝒃𝒃𝒃 𝒐𝒐𝒐𝒐𝒐𝒐 𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆
where, uj, vj, and wj are the fractional position of atoms in a unit cell.
𝒇𝒇 =
𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂 𝒐𝒐𝒐𝒐 𝒕𝒕𝒕𝒕𝒕𝒕 𝒘𝒘𝒘𝒘𝒘𝒘𝒘𝒘 𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔 𝒃𝒃𝒃𝒃 𝒂𝒂𝒂𝒂 𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂
𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂 𝒐𝒐𝒐𝒐 𝒕𝒕𝒕𝒕𝒕𝒕 𝒘𝒘𝒘𝒘𝒘𝒘𝒘𝒘 𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔 𝒃𝒃𝒃𝒃 𝒐𝒐𝒐𝒐𝒐𝒐 𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆𝒆
𝑰𝑰𝒉𝒉𝒉𝒉𝒉𝒉 𝜶𝜶 𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉
𝟐𝟐
NPTEL

52. Possible (hkl) planes for SCC lattice
(100), (010), (001), (110), (011), (111), (200), (020), (210), (120)...
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 𝒆𝒆𝟐𝟐𝝅𝝅𝒊𝒊(𝒉𝒉𝒖𝒖𝒋𝒋+𝒌𝒌𝒗𝒗𝒋𝒋+𝒍𝒍𝒘𝒘𝒋𝒋)
𝒖𝒖𝒋𝒋, 𝒗𝒗𝒋𝒋, 𝒘𝒘𝒋𝒋 = (𝟎𝟎, 𝟎𝟎, 𝟎𝟎)
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 𝒆𝒆𝟐𝟐𝝅𝝅𝒊𝒊×𝟎𝟎
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋
Diffraction will be observed for all sets of planes. There is no restriction in
hkl values to observed the diffraction patterns
Fractional position of jth atoms in a unit cell:
NPTEL

53. (110), (200), (211), (220).....
Possible (hkl) planes for BCC lattice
Fractional position of jth atoms in a unit cell:
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 𝒆𝒆𝟐𝟐𝝅𝝅𝒊𝒊(𝒉𝒉𝒖𝒖𝒋𝒋+𝒌𝒌𝒗𝒗𝒋𝒋+𝒍𝒍𝒘𝒘𝒋𝒋)
𝒖𝒖𝒋𝒋, 𝒗𝒗𝒋𝒋, 𝒘𝒘𝒋𝒋 = 𝟎𝟎, 𝟎𝟎, 𝟎𝟎 , (
𝟏𝟏
𝟐𝟐
,
𝟏𝟏
𝟐𝟐
,
𝟏𝟏
𝟐𝟐
)
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 [𝒆𝒆𝟐𝟐𝝅𝝅𝒊𝒊×𝟎𝟎+𝒆𝒆𝝅𝝅𝝅𝝅(𝒉𝒉+𝒌𝒌+𝒍𝒍)]
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 [𝟏𝟏 + 𝒆𝒆𝝅𝝅𝝅𝝅(𝒉𝒉+𝒌𝒌+𝒍𝒍)
]
Diffraction will be observed for particular sets of planes for which
(h+k+l)=even
(100), (111), (120), (122)...
Diffraction pattern will be observed
No diffraction pattern will be observed
𝒂𝒂
𝒄𝒄
𝒃𝒃
NPTEL

54. Possible (hkl) planes for FCC lattice
Fractional position of jth atoms in a unit cell:
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 𝒆𝒆𝟐𝟐𝝅𝝅𝒊𝒊(𝒉𝒉𝒖𝒖𝒋𝒋+𝒌𝒌𝒗𝒗𝒋𝒋+𝒍𝒍𝒘𝒘𝒋𝒋)
𝒖𝒖𝒋𝒋, 𝒗𝒗𝒋𝒋, 𝒘𝒘𝒋𝒋 = 𝟎𝟎, 𝟎𝟎, 𝟎𝟎 ,
𝟏𝟏
𝟐𝟐
,
𝟏𝟏
𝟐𝟐
, 𝟎𝟎 ,
𝟏𝟏
𝟐𝟐
, 𝟎𝟎,
𝟏𝟏
𝟐𝟐
, (𝟎𝟎,
𝟏𝟏
𝟐𝟐
,
𝟏𝟏
𝟐𝟐
)
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 [𝒆𝒆𝟐𝟐𝝅𝝅𝒊𝒊×𝟎𝟎
+𝒆𝒆𝝅𝝅𝝅𝝅(
𝒉𝒉
𝟐𝟐+
𝒌𝒌
𝟐𝟐+𝟎𝟎)
+ 𝒆𝒆𝝅𝝅𝝅𝝅(
𝒉𝒉
𝟐𝟐+𝟎𝟎+
𝒍𝒍
𝟎𝟎)
+ 𝒆𝒆𝝅𝝅𝝅𝝅(𝟎𝟎+
𝒌𝒌
𝟐𝟐+
𝒍𝒍
𝟐𝟐)
]
𝑭𝑭𝒉𝒉𝒉𝒉𝒉𝒉 = �
𝒋𝒋
𝒇𝒇𝒋𝒋 [𝟏𝟏 + 𝒆𝒆𝝅𝝅𝝅𝝅 𝒉𝒉+𝒌𝒌 + 𝒆𝒆𝝅𝝅𝝅𝝅(𝒉𝒉+𝒍𝒍) + 𝒆𝒆𝝅𝝅𝝅𝝅(𝒌𝒌+𝒍𝒍)]
Diffraction will be observed for particular sets of planes for which h,
k, and l is unmixed
(100), (120), (122), (311).....
Diffraction pattern will be observed
No diffraction pattern will be observed
(111), (200), (220), (311).....
𝒂𝒂
𝒄𝒄
𝒃𝒃
NPTEL

55. Incident X-Ray beam
Fluorescent X-Ray
Scattered X-Ray
Electron emission
Heat
Transmitted
X-ray beam
Compton
Modified
(Incoherent)
Unmodified
(Coherent)
Compton
Recoil
electron
Photoelectron
Auger
electron
Materials
NPTEL

56. Various XRD experimental setups
X-ray diffraction experimental set up requires an X-ray source, the sample under investigation and a detector
to pick up the diffracted X-rays.
Three variables:
a. Radiation : Monochromatic or of variable 
b. Sample : Single crystal, powder or solid piece
c. Detector : Radiation counter or photographic film
Wavelength Sample Detector Method
Monochromatic
Powder
Counter
Film
Diffractometer
Debye-Scherrer, Guiner
Single
crystal
Variable
Film
Counter
Rotation
Weissenberg
Precession
Automatic
diffractometer
Film
Solid piece Laue
NPTEL

57. Origin of X-ray production
X-rays are produced by impinging high energy electrons on a substrate (anode)
The X-ray spectrum is composed of two components
• A continuum
• Characteristic radiation
Cu
I
λ (Å)
Kβ
Kα1
Kα2
1s
2s
2p
3s
e-
2P→1S: Kα
3P→1S : Kβ
NPTEL

58. PROPERTIES OF X-RAYS
• Invisible electromagnetic rays
• Electrically neutral
• Wavelengths ≈ 0.04 – 1000 Å
• A white as well as characteristics radiation
• Velocity same as that of light
• Ionizing radiation
• They can cause fluorescence
• They affect photographic plate producing a latent image, which can be developed chemically
• They cannot be focused by a lens
• They produce chemical and biological changes
• Intensity of x-rays fall-off as inverse square of distance
• X-ray emerge from the tube in straight lines
• They produce secondary radiation
NPTEL

59. V
I
High Voltage
Generator
X-Ray
Tube
D
Amplifier Computer Printer
Voltage Stabilizer
Current Stabilizer
Sample
Collimator
Slits
Monochromator
Block Diargam Of XRD unit
NPTEL

60. Classical Powder Diffractometer
NPTEL

61. Sample preparation
•Typical penetration depth for Cu-Kα radiation is about 20 µm
•The crystallite size should be about 5 to 10 µm for a good statistical distribution
• Larger crystallite size : Poor statistics
•Too small crystallite size: Line broadening
•Grind the sample thoroughly so as to have narrow crystallite size distribution
•In case of pellets, prefer to use Isostatic press.
NPTEL

62. NPTEL

63. Handling reactive samples of which composition may change during
preparation, grinding or storage
•Use non-reactive wetting solution during grinding.
•Avoid all possible sources of contamination (e.g. handle metal powders in a
dry and inert atmosphere.
• Seal the sample with appropriate transparent media (Milar film)
Of course, the best method is to use a capillary for these samples.
After data collection is over:
Pattern treatment: Peak search, Background correction, smoothing,
Kα2 stripping
Data Processing: Indexing, Refinement of lattice parameters,
Structure refinement by Rietveld
NPTEL

64. Comparative X-Ray Scattering
Crystals
Amorphous
Solids or
Liquids
Monoatomic
gas
% I
2θ
10 20 30 40 50 60 70
Intensity
(arb.
unit)
2 Theta (Degree)
Polyaniline (PANi)
5 15 25 35 45
Intensity
(arb.
unit)
2 Theta (degree)
Activated Carbon
10 20 30 40 50 60 70
2 Theta (Degree)
Intensity
(arb.
unit)
Standard Silicon
NPTEL

65.  The crystal structure of any unknown solids can be determined by the X-ray diffraction
pattern.
 Various crystalline parameters can be calculated from the X-ray diffraction pattern.
 The reciprocal lattice and reciprocal lattice vector were discussed.
 The geometric structure factor of SCC, BCC, and FCC lattice were discussed
NPTEL

66. ⮚ “Introduction to Solid State Physics” by C. Kittel
⮚ “Solid State Physics” by Adrianus J. Dekker.
⮚ “Elements of X-ray diffraction” by B. D. Cullity.
NPTEL

67. Thank you…
NPTEL

68. Module 02: Synthesis protocols and crystal structures of materials
Lecture 12 : Crystal Imperfections
Physics of Functional Materials & Devices
Prof. Amreesh Chandra
Department of Physics, IIT KHARAGPUR
NPTEL

69. Concepts Covered
Void
Crack
 Crystal Imperfections
 Point Defects
 Line Defects
 Burger Vectors
 Interfacial Defects
NPTEL

70. Crystal imperfections
What do we mean by crystal defects or imperfections??
Crystalline defect refers to a lattice irregularity having
one or more of its dimensionson of the order of an
atomic diameter.
What is the need of studying imperfections in solid??
Till now we considered that perfect order exists
throughout the crystalline materials on an atomic
scale. However, such an idealized solid does not exist.
Rather, all contain large numbers of various defects or
imperfections. The properties of some materials are
profoundly influenced by the presence of these
imperfections.
Crystal defects are generally classified according to
the geometry or dimensionality of the defect.
Grain Boundary
Twin Boundary
Void
Crack
NPTEL

71. Point Defects and types:
NPTEL

72. Point defects are local
They concern just a few atoms close to the defect
Point Defects
 Vacancies : A vacancy = a missing atom in a lattice site
The simplest of the point defects is a vacancy, or vacant lattice site from
which an atom is missing. The necessity of the existence of vacancies is that
it increases the entropy (i.e. the randomness) of the crystal.
Vacancy defect also includes impurity atoms that occur in crystal lattices
and causes distortion. Impurity atoms occur either as:
An interstitial atom: an atom between the ordinary lattice sites.
A substitutional atom: an atom instead of a lattice atom in an ordinary site.
Interstitial atom
in crystal lattice
Substitutional atom
and vacancy in crystal lattice
Crystal lattice
NPTEL

73.  Frenkel Defect :
This defect forms when an atom or smaller ion (usually cation) leaves its
place in the lattice, creating a vacancy and becomes an interstitial by lodging
in a nearby location.
 Difference between self-interstitial defect & interstitial defect :-
Self-interstitial defect occurs when atom of the same crystalline solid
occupies the interstitial position leaving its original lattice site, whereas in
case of interstitial defect a foreign atom occupies the interstitial position.
 Self-interstitial Defect :
These defects are interstitial defects, which occurs when atom of the same
crystalline solid occupies the interstitial position leaving its original lattice
site.
No ions are missing from crystal lattice as a whole in Frenkel Defect, thus the
density of solid and its chemical properties remain unchanged as well as the
crystal as a whole remains electrically neutral.
Point Defects
NPTEL

74. Line Defects and their types:
NPTEL

75. Line Defects
Dislocations are line defects in the crystal lattice
They are created when there is a deviation from the ideal crystal structure in a plane or a line of atoms, resulting in irregularity in a
complete line, of crystalline solid.
Line defects can have a significant impact on the properties of a material, such as its mechanical strength and electrical
conductivity. They can also affect the behavior of other defects in the material, such as point defects or grain boundaries. Based on
the nature of deviation line defect can be classified into two types:
 Mixed dislocations: Most dislocations found in crystalline materials are probably neither purely edge nor purely screw
type. Rather, it exhibits components of both types; these are termed mixed dislocations.
 Edge dislocations: An extra portion of a plane of atoms, or half-plane, whose edge terminates within the crystal. This
is sometimes termed the dislocation line,
 Screw dislocations: Screw dislocation is another type of line defect in which the defect
occurs when the planes of atoms in the crystal lattice trace a helical path around the
dislocation line
NPTEL

76. Before, we learn types of line defects in detail, we need to understand what is Burgers vector????
 The magnitude and direction of the lattice distortion associated with a dislocation are expressed in terms of a Burgers
vector, denoted by b.
 The magnitude of the Burgers vector determines the strength of the dislocation, with larger vectors corresponding to
stronger dislocations. The direction of the Burger's vector also affects the behavior of the dislocation, such as its motion
under applied stress.
 The Burgers vector can be either edge or screw type, depending on the type of dislocation.
 Even if a dislocation changes direction and nature within a crystal (e.g., from edge to mixed to screw), the Burgers
vector is the same at all points along its line
Burger vector is perpendicular to the dislocation line, for edge dislocation
Burger vector is parallel to the dislocation line, for screw dislocation
Burgers vector
NPTEL

77. • An edge dislocation is a type of linear crystallographic defect in a crystal lattice where an extra half-plane of atoms is
inserted between two planes of atoms, resulting in a region of localized strain. The dislocation line is the boundary
between the planes of atoms.
• In an edge dislocation, the Burger's vector is perpendicular to the dislocation line and points from the compressed side to
the tensile side of the lattice. The compressed side has a higher atomic density than the tensile side, and the extra half-
plane of atoms in the dislocation region accommodates this mismatch.
• Edge dislocations can be created by a variety of mechanisms, such as plastic deformation, thermal stresses, or impurity
atoms. These dislocations play a critical role in determining the mechanical properties of materials, such as their
strength and ductility.
Edge Dislocation
Fig.: Edge Dislocation
 Edge Dislocation
NPTEL

78.  Screw Dislocation
• A screw dislocation is a type of linear crystallographic defect in a crystal lattice where the lattice is distorted by a shear
deformation along a single plane. The dislocation line is the axis around which the lattice is twisted.. Sometimes the
symbol is used to designate a screw dislocation.
• This type of dislocation can be visualized as a spiral staircase, with the dislocation line running up the center of the
staircase. In a screw dislocation, the Burger's vector is parallel to the dislocation line
• A screw dislocation converts a pile of crystal planes into a single continuous helix. When the helix intersects the surface
a step is formed, which cannot be eliminated by adding further atoms. The crystal grows as a never-ending spiral.
Screw Dislocation
Fig.: Screw Dislocation
NPTEL

79. Interfacial Defect and its types:
NPTEL

80. Interfacial Defects
Interfacial defects are defects that occur at the interface between two materials or between two regions within the same
material that have different crystal structures, chemical compositions, or physical properties.
 Stacking Faults
 A stacking fault is created when there is a deviation from the regular stacking sequence of
planes in the crystal lattice along a particular crystallographic direction.
 Stacking faults are not expected in crystals with ABAB sequences in, Therefore, it does not
occurs in BCC structures, as there is no alternative for an A layer resting on a B layer,
whereas, it takes place in FCC structure.
 An intrinsic stacking fault is the change in sequence resulting from the removal of a layer.
An extrinsic stacking fault is the change in sequence resulting from an introduction of an
extra layer.
 Stacking Faults
 Grain Boundaries
 Twin dislocations:
 Interfacial defect can be classified into three types:
Fig.: Intrinsic Stacking Fault Fig.: Extrinsic Stacking Fault
Stacking Fault
NPTEL

81. Interfacial Defects
 Grain Boundaries
 Crystalline metals consist of aggregates of small crystals with mutually different orientations called grains. The interfaces
between these grains are called grain boundaries
 A grain boundary is equivalent to a dense array of static dislocations. It works like a high barrier to moving dislocations.
The grain boundaries promote hardening.
 The mechanical strength of a crystal is inversely proportional to the average grain diameter. The smaller the grains are, the
better will be the mechanical properties of the material.
 Grain boundaries are often irregular and have a higher energy than the ideal lattice, as the arrangement of atoms across the
boundary is not perfect.
NPTEL

82.  Twinned Crystals
 A twin boundary is a special type of grain boundary across which there is a specific mirror lattice symmetry; i.e. atoms on one
side of the boundary are located in mirror-image positions of the atoms on the other side. The region of material between these
boundaries is appropriately termed a twin.
 The two main kinds of symmetry operations are
180o rotation about an axis, called the twin axis
 Reflection across a plane, called he twin plane
 Twinning can occur during crystal growth or as a result of mechanical deformation. The twinned regions may have different
physical or chemical properties, such as different lattice parameters, crystal structures, or orientation-dependent properties like
optical birefringence or electrical conductivity
I
II
Fig.: Twinned Crystals
NPTEL

83. Questions:
1) How can you limit defects?
2) What will happen when materials are obtained in different batches?
3) Will the different synthesis routes lead to same order or types of defects?
4) How will you characterize defects?
5) Are defects always BAD?
NPTEL

84. The concepts of crystal imperfections are described.
Different types of crystal imperfections including line defects, point defects, and
interfacial defects are described.
NPTEL

85.  Physics of Functional Materials by Hasse Fredriksson and Ula Akerlind.
 Imperfections in Crystalline Solids by Wei Cai and William D. Nix.
NPTEL

86. Thank you…
NPTEL

87. Module 02: Synthesis protocols and crystal structures of materials
Lecture 13 : Alloys & melts
Physics of Functional Materials & Devices
Prof. Amreesh Chandra
Department of Physics, IIT KHARAGPUR
NPTEL

88.  What are alloys?
 Hume-Rothery’s rules
 Solid solution and its types
 Types of Random Solid solution
 Primary & Secondary Solid solution
 Substitutional solid
 Interstitial solid solution
NPTEL

89. An alloy is a combination of a metal with at least one other metal or nonmetal.
An alloy can be characterized as a metallic liquid or solid, consisting of a close combination of two or more elements.
Often, one metal occurs in a high concentration. It is called the parent metal or solvent.
Any chemical element can be used as an alloying element or solute.
What happens when parent material is dissolved in an alloying metal?
Every system want to reach its minimum energy level. When parent material is dissolved in alloying metal, atoms get displaced in
the crystal lattice, they change their sizes as a function of composition of the solid solution, new phases and chemical compound
appears, clusters or superlattices are formed in order to attain energy minima.
In order to understand these effects
qualitatively, we will discuss the
structures of various types of solid
alloys….
Alloys
NPTEL

90. The composition of an alloy cannot be chosen arbitrarily !!!
The metals must form a solid solution and intermediate phases must be avoided.
In order to gauge whether the metals in the planned proportions can form a solid substitutional solution or
not, Hume-Rothery presented a set of rules:
Hume-Rothery’s rules
Before, we learn structures of solid it is important to note that:-
1. The Relative Size Rule
2. The Electrochemical Rule
3. The Relative Valance Rule
4. The Lattice Type Rule
NPTEL

91. Size factor = 𝟏𝟏 +
𝒓𝒓𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔 − 𝒓𝒓𝒓𝒓𝒓𝒓𝒓𝒓𝒓𝒓𝒆𝒆𝒆𝒆𝒆𝒆
𝒓𝒓𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒔𝒕𝒕
If,
Size factor > 1.14 = Unlikely that a solid solution can form and the solubility will be low.
Size factor < 1.08 = A complete solid solution can be obtained.
Hume-Rothery’s rules
1. The Relative Size Rule:
The more the solute atom differs in size from the solvent, the lower will be the solubility of the metal. This is described with
the help of a relative size factor, defined as:
NPTEL

92. Hume-Rothery’s rules
2. The Electrochemical Rule :
3. The Relative Valance Rule :
4. The Lattice Type Rule :
The more electropositive one of the metals is and the more electronegative the other one is, the lower will be
the solubility of the two metals. If the difference in chemical affinity of the two metals is large, the two
atoms form a compound instead of a solid solution.
If the alloying metal and the basic metal differ in valence, the electron ratio, i.e. the average number of
valence electrons per atom, will be changed by alloying. Crystal structures are more sensitive to a decrease in
the number of electrons than to an increase. This is the reason why a high-valence metal dissolves a low-valence
metal poorly, whereas a low-valence metal may dissolve a high-valence metal well.
Only metals with identical lattice structures are completely miscible, i.e. can form
solid solutions of any proportions.
NPTEL

93. Hume-Rothery’s rules
Important points :
• There are exceptions to Hume-Rothery’s rules, but overall they are very useful in
predicting qualitative solubilities of metals.
• The first rule is a necessary but not sufficient condition. If the relative size factor is
disadvantageous, the solubility of the metals will be poor, even if the other conditions
are fulfilled.
NPTEL

94. 1. Random solid solution: Random solid solutions are a type of solid solution where the solute atoms are distributed
randomly throughout the solvent crystal lattice, resulting in a material with unique properties compared to pure
materials. Examples: Brass, stainless steel etc.
2. Ordered solid solutions: In an ordered solid solution, the solute atoms occupy specific lattice sites in the solvent
crystal lattice, resulting in an ordered arrangement. They have long-range atomic arrangements, resulting in unique
properties such as superconductivity or magnetism. Examples: NiAl, which has an ordered structure.
Solid solutions are homogeneous mixtures of two or more substances that exist in a solid state.
The properties of a solid solution depends on the nature and amount of the solute and solvent atoms, as well as the
crystal structure and composition of the material.
Solid solution can be classified into two types:
Solid solution and its types:
NPTEL

95. Random solid solutions are classified on the basis of solute-solvent composition and their position.
Random Solid
Solution
On the basis of
solute-solvent
composition
Primary solid
solution
Secondary solid
solution
On the basis of
solute-solvent
position
Substitutional
solid
Interstitial solid
Types of Random Solid Solutions
NPTEL

96. The composition of homogeneous alloys is possible only within certain limits
 Primary solid solution: In a primary solid solution, the atoms of each element are evenly distributed throughout the crystal
lattice and are not segregated into distinct regions or phases. Primary solid solutions are often formed in alloys, which are
mixtures of metals or a metal and includes one pure component of the alloy.
Example: Brass alloy, where copper and zinc in their pure form can dissolve in each other to form a single-phase alloy.
Primary solid solutions
NPTEL

97. Secondary solid solutions are also known as intermediate phase.
 Secondary solid solution: When an alloying element is added to a base metal in such quantities that the limit of solid
solubility is exceeded, a secondary or intermediate phase appears. It can occur through the substitution of atoms of different
element in the lattice of the primary solid solution. The secondary phase can be another solid solution, a chemical compound
or a phase with a structure other than the one of the primary solid solution.
Example: In the brass alloy, if small amounts of another element such as tin or aluminum are added, they substitute for
either copper or nickel atoms in the lattice and form a secondary solid solution. This can alter the properties of the alloy, such
as its strength, hardness, and ductility.
Secondary solid solutions
NPTEL

98. Secondary solid solutions are classified on the basis of their structures.
They can be classified as:
1. Electrochemical Compounds: The solute atoms or ions substitute for the solvent atoms or ions in the crystal lattice but with
a different valence state or electronic charge, resulting in different electronic properties. They obey the valence law and are
formed by electropositive and electronegative elements. Examples:Mg2Si and ZnS
2. Size Factor Compounds: The size factor compounds have compositions and structures that correspond to the lowest
possible energies, lower than the sum of the energies of the separate components. The component atoms in size factor
compounds are closely packed and have often high coordination numbers. Examples: FeCr, CoCr and FeV
3. Electron Compounds: Electron ratio plays a crucial role in the appearance of intermediate phases,
Electron ratio= 𝑁𝑁𝑁𝑁𝑁𝑁𝑁𝑁𝑁𝑁𝑁𝑁 𝑜𝑜𝑜𝑜 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒/𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴
They are formed at definite compositions, i.e. definite values of the electron ratio of the alloy, and vary also with the structure of the
crystal lattice.
Secondary solid solutions
NPTEL

99. Solid solutions are either substitutional or interstitial
This type of solution has a great influence on the properties of the alloy.
 Substitutional solid: In a substitutional solid solution, the alloying atoms/ solute atoms replace some of the parent atoms in the
crystal lattice. These solutions have a significant impact on the physical, mechanical, and chemical properties of materials,
making them useful in a variety of industrial applications. Example: brass alloy, which is a mixture of iron and carbon. Here,
zinc atoms substitute for some of the copper atoms in the crystal lattice of the material, making it stronger and harder than pure
iron.
Substitutional solid
Substitutional Solid solution
NPTEL

100.  Interstitial solid: In an interstitial solid, the solute atoms (usually small in size) occupy the spaces or interstices between the
solvent atoms, filling the lattice. Example: titanium alloys, where small amounts of elements such as oxygen, nitrogen, and
carbon are added to the titanium lattice to create a stronger and more durable material.
Interstitial solid
Alloys can consist of both interstitial and substitutional solid solutions at the same time
Example: stainless steels, which contain interstitially dissolved carbon together with
substitutionally dissolved chromium, nickel and/or other metals.
Interstitial solid solution
NPTEL

101. Alloys can consist of both interstitial and substitutional solid solutions at the same time
Example: stainless steels, which contain interstitially dissolved carbon together with
substitutionally dissolved chromium, nickel and/or other metals.
1. The only alloying elements which are small enough to form interstitial solid solutions are H, C, N and B.
2. The lattice rule plays an important role in forming interstitial solid solutions. Example: The solubility of carbon in
austenite (FCC structure) is about eight times higher than in ferrite (BCC structure) . The difference in solubility of
carbon between austenite and ferrite depends on the available space for C atoms. An FCC structure offers much more
space for interstitials than a BCC structure.
3. The hydrides, nitrides, carbides and borides of the transition metals are important groups of interstitial solid solutions.
4. The interstitial solutions are genuine alloys with metallic properties.
 Application: The interstitial solid solution of carbon in iron is the basis of steel hardening.
 Properties of interstitial solid solution::
Interstitial solid solution
NPTEL

102. The definition of alloys is discussed.
Hume-Rothery’s rule were described.
Various kind of solid solutions are highlighted.
NPTEL

103.  Physics of Functional Materials by Hasse Fredriksson and Ula Akerlind.
NPTEL

104. Thank you…
NPTEL