Operation research emerged from efforts during World War II to apply scientific methods to solve complex military problems. Its use expanded to business and industry after the war to address problems caused by increasing organizational complexity and specialization. Operation research uses interdisciplinary teams and quantitative modeling to analyze problems from a total system perspective, seeking optimal solutions that balance conflicting objectives across an organization. It has been applied in diverse fields like manufacturing, transportation, healthcare, and more. Key techniques include linear programming, queuing theory, and simulation. The scientific method and building mathematical models are core to the operation research approach to problem solving.









![OPERATION RESEARCH MGMT 441
10 | P a g e
or the constraints or both can be non-linear functions, which would require altogether different
solution technique.
USES OF OPERATIONS RESEARCH
In its recent years of organized development, OR has entered successfully many different areas
of research for military government and industry in many countries of the world.
The basic problem in most of the developing countries in Asia and Africa is to remove poverty
and improve the standard of living of a common man as quickly as possible. So there is a great
scope for economists, statisticians, administrators, politicians and the technicians working in a
team to solve this problem by an OR approach. The possible application sectors, in Pakistan, are
as under:-
1) Macro Economic Planning:
OR can be employed for Macro-Economic Planning of the country:
a) Input / Output Analysis: by using LP models. This input/output analysis can be of any
duration [i.e. of short term (up to say 10 years)-Five Year Plan; and of long term (10-30 years)].
b) Investment Planning: OR can be employed in the Investment Planning of the country where
investment plans for the next five or ten years are prepared. Mixed Integer Programming and
Linear Programming techniques can be used.](https://image.slidesharecdn.com/ornote-231201083907-8f5a09cc/85/OR-note-pdf-10-320.jpg)








































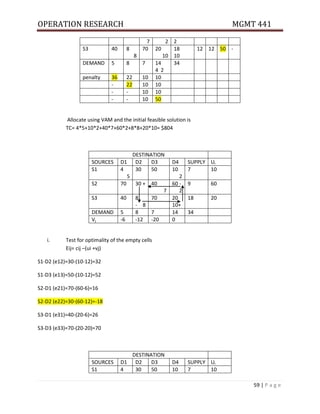










![OPERATION RESEARCH MGMT 441
70 | P a g e
E. Train the operator 6 C
F. Produce the product 1 D.F
Critical path Analysis
After the project network is drown and activity time is known, we can determine
The total time needed to complete the whole project.
When different activities may be scheduled
Which activities are critical & non-critical?
The critical path by doing forward and backward pass calculations.
Float for each activity the amount of time by which the completion of an activity can be
delayed without delaying the total project completion time.
Forward pass calculations give earliest start time (EST) and Earliest finish time (EFT) for each
activity. While backward pass calculations gives latest start time (LST) and latest finish time (LFT)
for each activity.
EFT = EST + Activity duration forward pass calculation
LST = LFT – Activity duration backward pass calculation.
Notation: Activity, Duration [EST, EFT]
[LST, LFT]
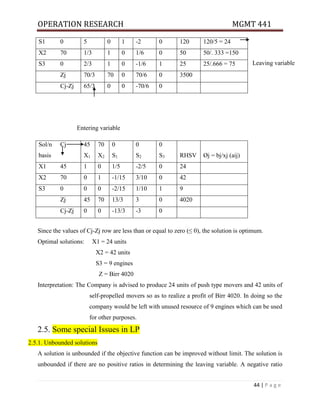
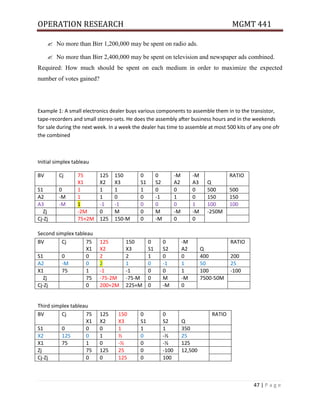
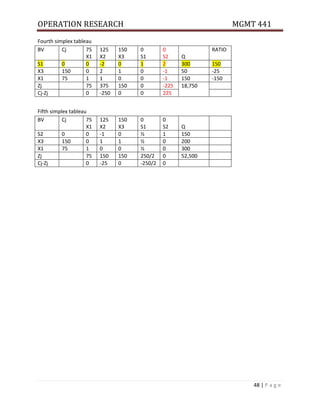
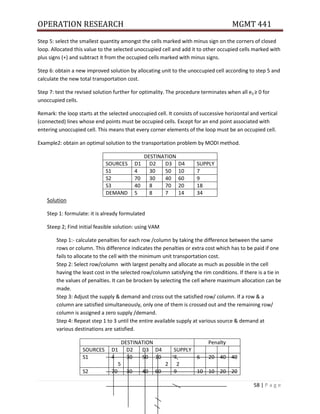
Example 2: Information on the activities required for a project is as follows.
Activity name A B C D E F G H I J K
Activity Node 1-2 1-3 1-4 2-5 3-5 3-6 3-7 4-6 5-7 6-8 7-8
Duration Analysis 2 7 8 3 6 10 4 6 2 5 6
Draw the network & calculate EST, EFT, LST &LFT for each activity.
Determine the critical path, critical activities and the project duration
D 3[2,5]
A2[0,2] E6[713] I2[13,15]
B7[0,7] G4[7,11] K6[15,21]
C8[0,8] J5[17,22]
H6[8,14]
1
2
4
3
5
6
7 8](https://image.slidesharecdn.com/ornote-231201083907-8f5a09cc/85/OR-note-pdf-70-320.jpg)

