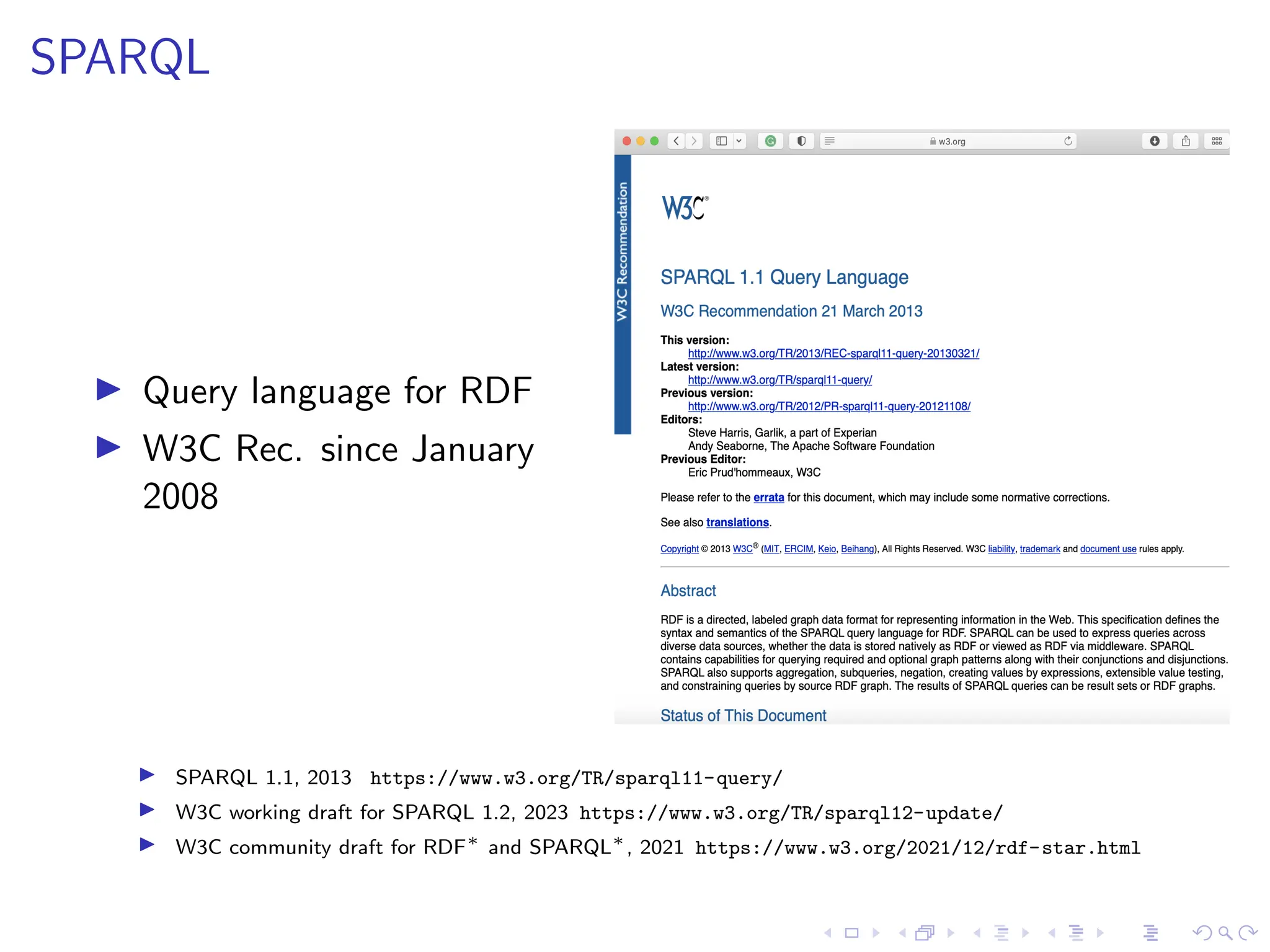
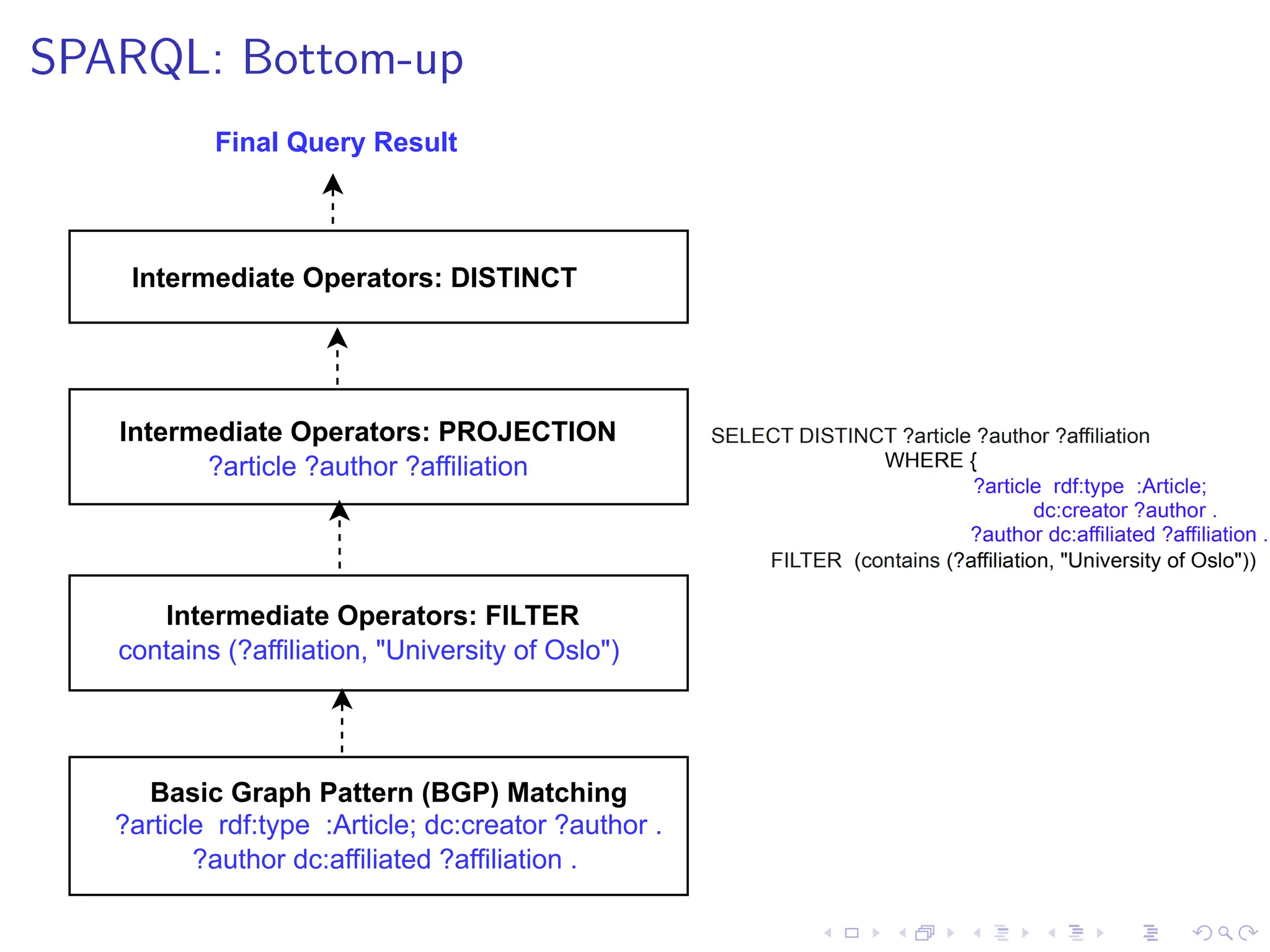
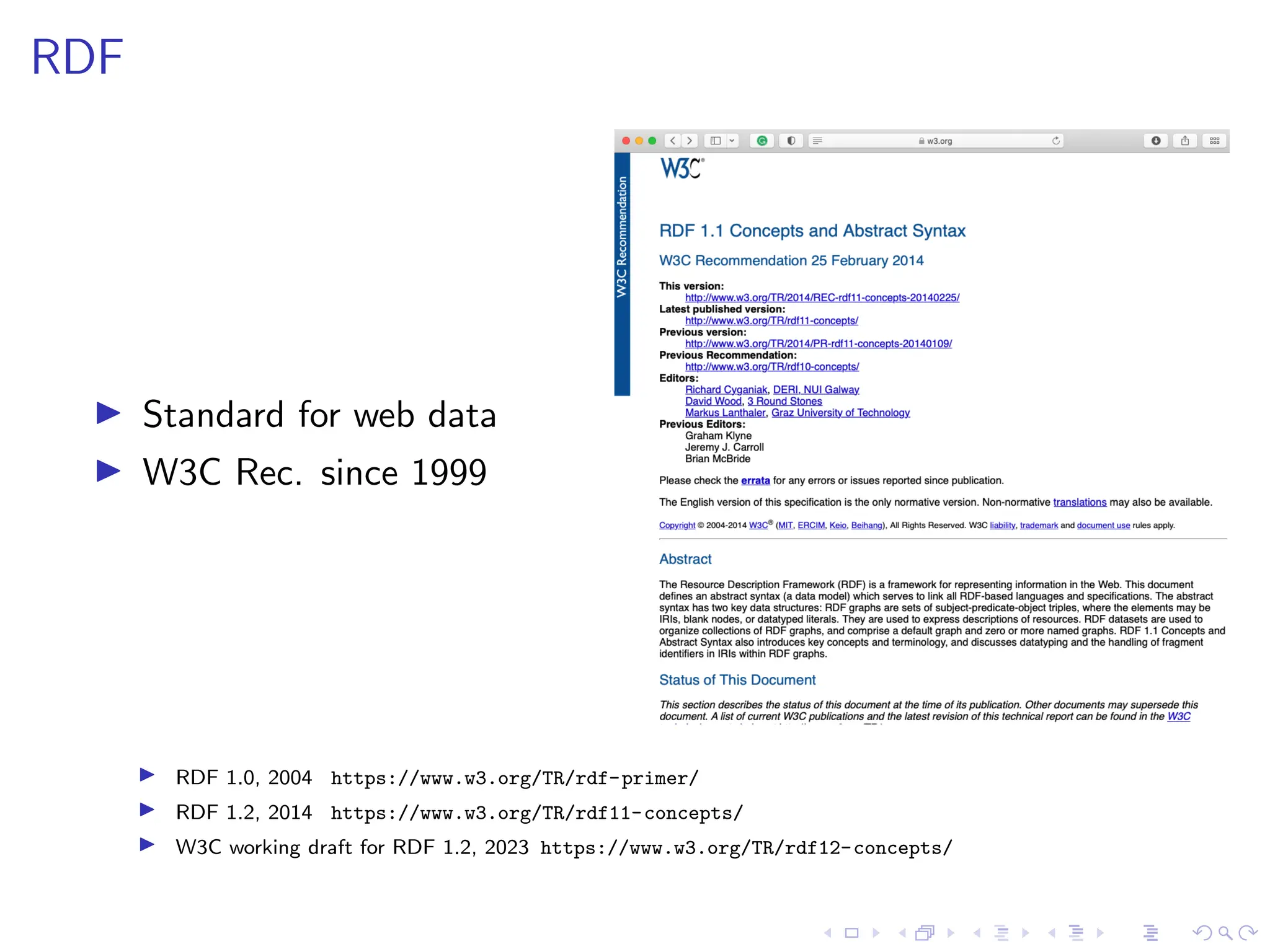
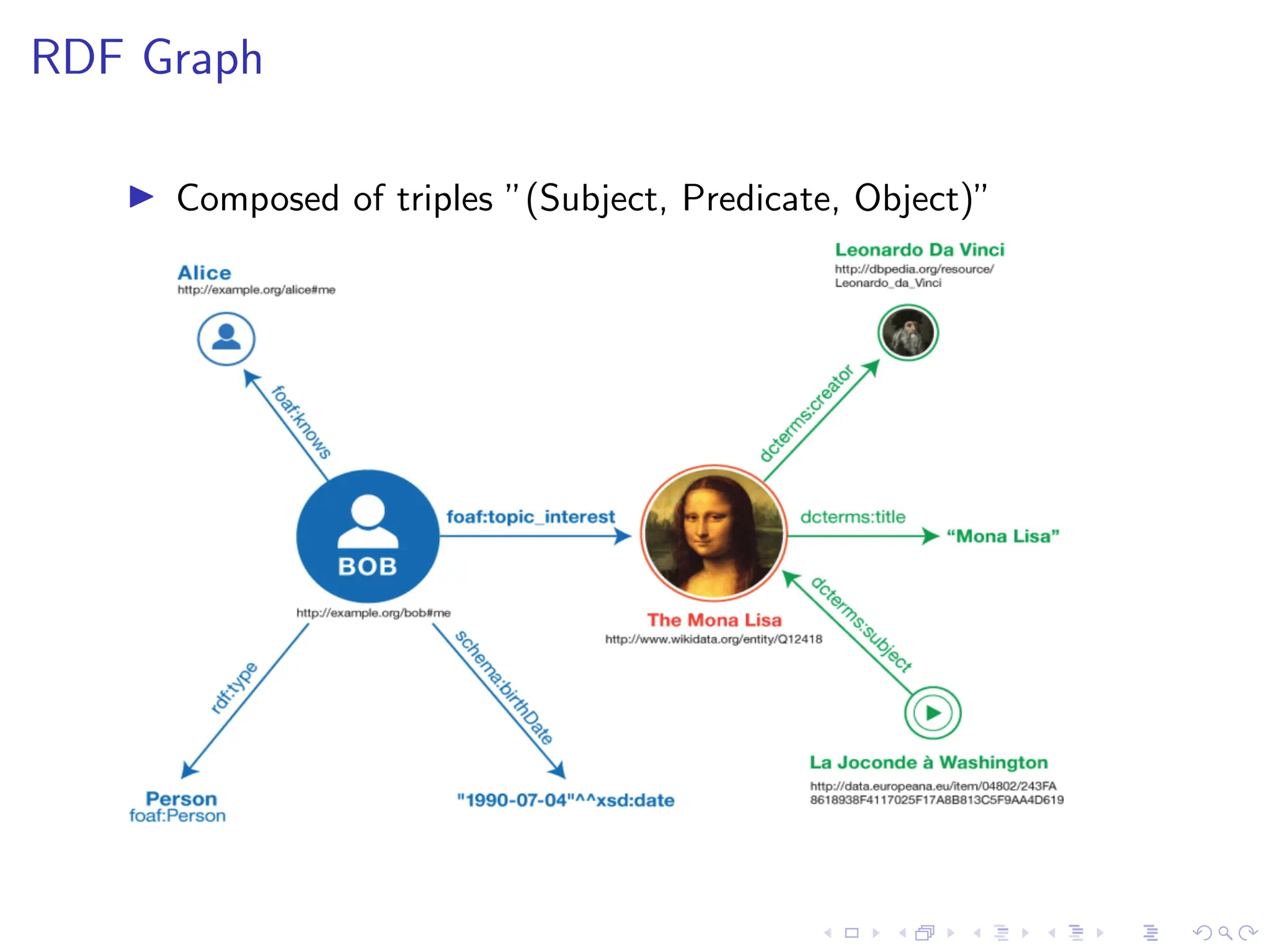
The document presents a comprehensive overview of RDF, SHACL, and SPARQL, including their syntaxes, constraints, and validation processes. It details the evolution of RDF standards and introduces SHACL as a constraint language for RDF, alongside multiple examples of its use. The document also covers query patterns, optimization techniques in SPARQL, and the grammar for querying RDF graphs.





![SHACL
▶ relies on the notion of ”shapes”
e.g.,
:EmployeeNode a sh:NodeShape;
sh:targetClass :Employee;
sh:property [ sh:path :hasAddress;
sh:nodeKind sh:Literal;
sh:maxCount 1; sh:minCount 1;
sh:datatype xsd:string ];
sh:property [ sh:path :hasAddress;
dash:uniqueValueForClass
:Employee ].](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-9-2048.jpg)
![SHACL Shape
▶ relies on the notion of ”shapes”
e.g.,
:EmployeeNode a sh:NodeShape ;
sh:targetClass :Employee ;
sh:property [ sh:path :hasAddress ;
sh:nodeKind. sh:Literal ;
sh:maxCount 1;
sh:minCount 1;
sh:datatype xsd:string ];
sh:property [ sh:path :hasAddress;
dash:uniqueValueForClass
:Employeee ].
shape name
target defn
constraints
defn](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-10-2048.jpg)
![SHACL: Constraint Validation
Consider an RDF graph on the left and a SHACL shape on the right, written in
Turtle syntax:
:Ida a :Employee;
:hasID "001"^^xsd:int;
:hasAddress "Oslo".
:Ingrid a :Employee;
:hasID "002"^^xsd:int;
:hasAddress "Bergen".
:EmployeeNode a sh:NodeShape;
sh:targetClass :Employee;
sh:property [ sh:path :hasAddress;
sh:nodeKind sh:Literal;
sh:maxCount 1; sh:minCount 1;
sh:datatype xsd:string ];
sh:property [ sh:path :hasAddress;
dash:uniqueValueForClass
:Employee ].](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-11-2048.jpg)
![SHACL: Constraint Validation
Acquiring Target nodes:
:Ida a :Employee;
:hasID "001"^^xsd:int;
:hasAddress "Oslo".
:Ingrid a :Employee;
:hasID "002"^^xsd:int;
:hasAddress "Bergen".
:EmployeeNode a sh:NodeShape;
sh:targetClass :Employee;
sh:property [ sh:path :hasAddress;
sh:nodeKind sh:Literal;
sh:maxCount 1; sh:minCount 1;
sh:datatype xsd:string ];
sh:property [ sh:path :hasAddress;
dash:uniqueValueForClass
:Employee ].](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-12-2048.jpg)
![SHACL: Constraint Validation
Checking compliance of Target nodes against Constraints : VALID
:Ida a :Employee;
:hasID "001"^^xsd:int;
:hasAddress "Oslo".
:Ingrid a :Employee;
:hasID "002"^^xsd:int;
:hasAddress "Bergen".
:EmployeeNode a sh:NodeShape;
sh:targetClass :Employee;
sh:property [ sh:path :hasAddress;
sh:nodeKind sh:Literal;
sh:maxCount 1; sh:minCount 1;
sh:datatype xsd:string ];
sh:property [ sh:path :hasAddress;
dash:uniqueValueForClass
:Employee ].](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-13-2048.jpg)
![SHACL: Propagated Constraint Validation
:EmployeeNode a sh:NodeShape;
sh:targetClass :Employee;
sh:property [ sh:path :hasAddress;
sh:nodeKind sh:Literal;
sh:maxCount 1; sh:minCount 1;
sh:node :AddressNode ].
:AddressNode a sh:NodeShape;
sh:property [ sh:path :telephone;
sh:maxCount 1; ];
sh:property [ sh:path :locatedIn;
sh:maxCount 1; sh:minCount 1;
sh:value :NorthernNorway; ];](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-14-2048.jpg)
![SHACL: Propagated Constraint - ”Recursion”?
:EmployeeNode a sh:NodeShape;
sh:targetClass :Employee;
sh:property [ sh:path :hasAddress;
sh:nodeKind sh:Literal;
sh:maxCount 1; sh:minCount 1;
sh:node :AddressNode ];
sh:property [ sh:path :knows;
sh:minCount 1;
sh:node :EmployeeNode ].
:AddressNode a sh:NodeShape;
sh:property [ sh:path :telephone;
sh:maxCount 1; ];
sh:property [ sh:path :locatedIn;
sh:maxCount 1; sh:minCount 1;
sh:value :NorthernNorway; ].](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-15-2048.jpg)
![SHACL: Propagated Constraint - ”Recursion”?
:EmployeeNode a sh:NodeShape;
sh:targetClass :Employee;
sh:property [ sh:path :hasAddress;
sh:nodeKind sh:Literal;
sh:maxCount 1; sh:minCount 1;
sh:node :AddressNode ];
sh:property [ sh:path :knows;
sh:minCount 1;
sh:node :EmployeeNode ].
:AddressNode a sh:NodeShape;
sh:property [ sh:path :telephone;
sh:maxCount 1; ];
sh:property [ sh:path :locatedIn;
sh:maxCount 1; sh:minCount 1;
sh:value :NorthernNorway; ].
From : https://www.w3.org/TR/shacl/
Recursion
Not 100% formal semantics
Validation explicitly left undefined](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-16-2048.jpg)
![SHACL: Propagated Constraint - ”Recursion”
:EmployeeNode a sh:NodeShape;
sh:targetClass :Employee;
sh:property [ sh:path :hasAddress;
sh:nodeKind sh:Literal;
sh:maxCount 1; sh:minCount 1;
sh:node :AddressNode ];
sh:property [ sh:path :knows;
sh:minCount 1;
sh:node :EmployeeNode ].
:AddressNode a sh:NodeShape;
sh:property [ sh:path :telephone;
sh:maxCount 1; ];
sh:property [ sh:path :locatedIn;
sh:maxCount 1; sh:minCount 1;
sh:value :NorthernNorway; ].
Contributions:
Abstract syntax of SHACL core
Semantics for recursive SHACL
Validation algorithms and Tractable fragments](https://image.slidesharecdn.com/optimizingsparqlquerieswithshacl-231019195734-2220ad80/75/Optimizing-SPARQL-Queries-with-SHACL-pdf-17-2048.jpg)