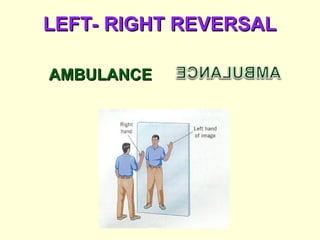
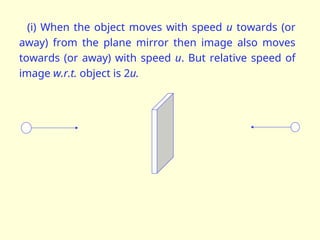
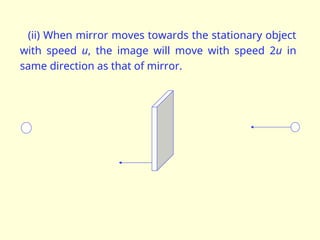
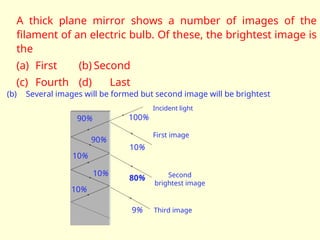
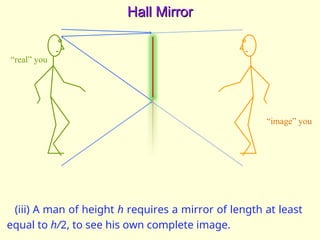
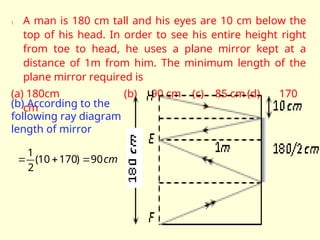
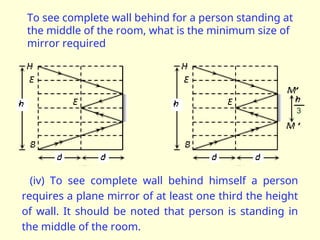
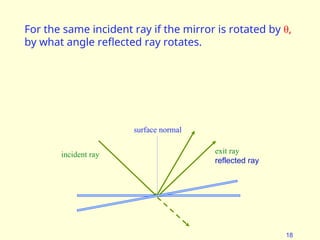
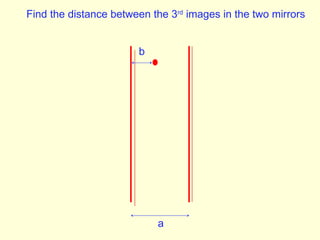
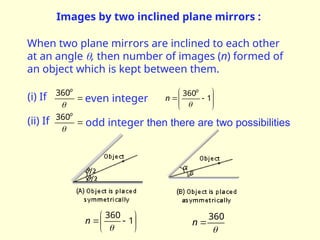
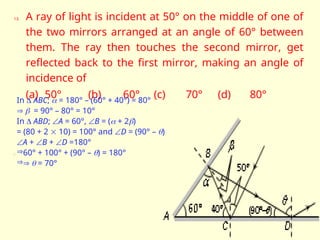
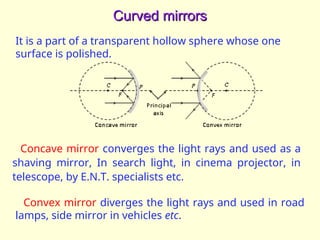
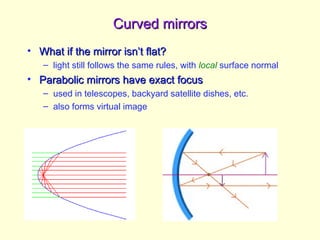
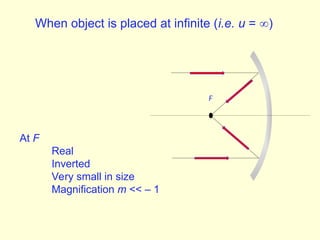
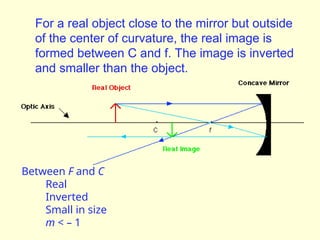
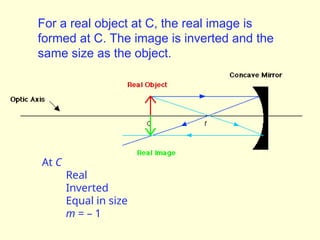
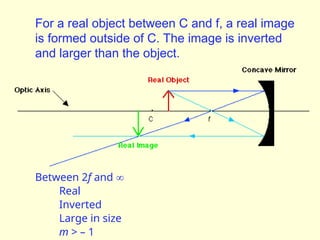
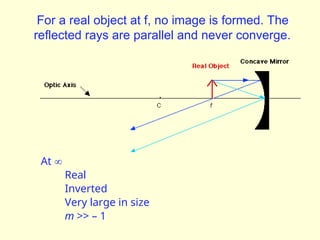
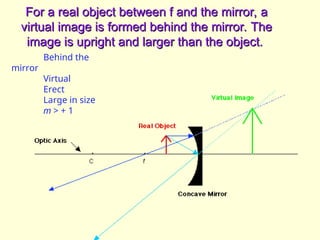
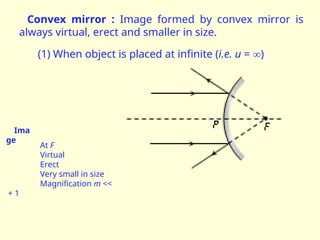
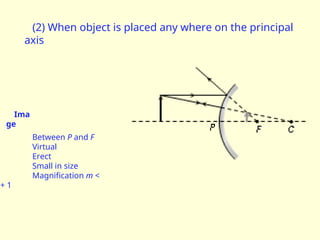
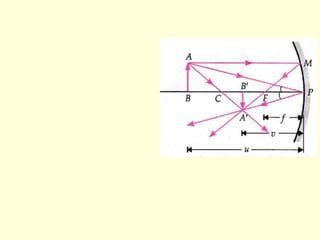
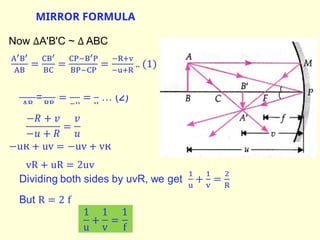
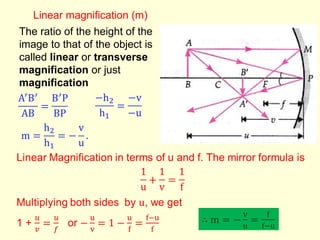
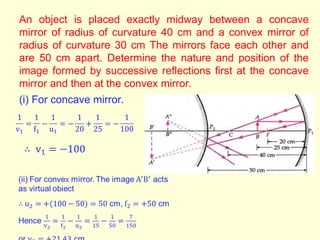
The document discusses the principles of ray optics, focusing on reflection and the behavior of light with plane and curved mirrors. It explains key concepts such as the laws of reflection, real versus virtual images, and the characteristics of different types of mirrors, including concave and convex mirrors. It also includes practical applications and mathematical relationships related to the formation of images and their magnification in various mirror types.

1. Ray Optics
Ray Optics
Plane and spherical Mirrors
Plane and spherical Mirrors

2. Light ray
The path along which light energy travels is called a RAY
It is represented by a straight line with an arrow to
show its direction of motion.

3. BEAM OF LIGHT
A beam of light is a bundle of light rays
Parallel beam
diverging beams
converging beams

4. Reflection
Reflection
• We describe the path of light as straight-line rays
We describe the path of light as straight-line rays
• Reflection off a flat surface follows a simple rule:
Reflection off a flat surface follows a simple rule:
– angle in (incidence) equals angle out (reflection)
– angles measured from surface “normal” (perpendicular)
surface normal
same
angle
incident ray exit ray
reflected ray
i r

5. Reflection
Reflection
surface normal
same
angle
incident ray exit ray
reflected ray
i r
When a ray of light incident on a boundary
separating two media comes back into the same
media, then this phenomenon, is called reflection of
light.

6. Reflection
Reflection
surface normal
same
angle
incident ray exit ray
reflected ray
i r
Laws of Reflection:
I Law: The incident ray, the normal to the reflecting surface at the point
of incidence and the reflected ray all lie in the same plane.
II Law: The angle of incident i is equal to the angle of reflection r
i = r

7. REAL AND VIRTUAL IMAGES
REAL AND VIRTUAL IMAGES
If light rays, after reflection or refraction, actually
meets at a point then real image is formed and if they
appears to meet virtual image is formed.

8. Virtual Images in Plane Mirrors
If light energy doesn't flow from the
image, the image is "virtual".
Rays seem to come from behind
the mirror, but, of course, they
don't. It is virtually as if the rays
were coming from behind the
mirror.
"Virtually": the same as if
As far as the eye-brain system is
concerned, the effect is the same
as would occur if the mirror were
absent and the chess piece were
actually located at the spot labeled
"virtual image".

9. 9
Reflection From a Plane Surface (Plane Mirror)
The image formed by a plane mirror is
1) Virtual,
2) Erect (laterally inverted)
3) Equal in size that of the object
and at a distance equal to the distance of the object in
front of the mirror.
x x

10. LEFT- RIGHT REVERSAL
LEFT- RIGHT REVERSAL
AMBULANCE
AMBULANCE

11. (i) When the object moves with speed u towards (or
away) from the plane mirror then image also moves
towards (or away) with speed u. But relative speed of
image w.r.t. object is 2u.

12. (ii) When mirror moves towards the stationary object
with speed u, the image will move with speed 2u in
same direction as that of mirror.

13. A watch shows time as 3:25 when seen through a
mirror, time appeared will be
35
:
8

14. A thick plane mirror shows a number of images of the
filament of an electric bulb. Of these, the brightest image is
the
(a) First (b) Second
(c) Fourth (d) Last
100%
90%
90%
10%
10%
10%
10%
80%
9%
First image
Second
brightest image
Third image
Incident light
(b) Several images will be formed but second image will be brightest

15. Hall Mirror
Hall Mirror
“image” you
“real” you
(iii) A man of height h requires a mirror of length at least
equal to h/2, to see his own complete image.

16. 1. A man is 180 cm tall and his eyes are 10 cm below the
top of his head. In order to see his entire height right
from toe to head, he uses a plane mirror kept at a
distance of 1m from him. The minimum length of the
plane mirror required is
(a) 180cm (b) 90 cm (c) 85 cm (d) 170
cm
(b) According to the
following ray diagram
length of mirror
cm
90
)
170
10
(
2
1




17. (iv) To see complete wall behind himself a person
requires a plane mirror of at least one third the height
of wall. It should be noted that person is standing in
the middle of the room.
3
To see complete wall behind for a person standing at
the middle of the room, what is the minimum size of
mirror required

18. 18
For the same incident ray if the mirror is rotated by θ,
by what angle reflected ray rotates.
surface normal
incident ray exit ray
reflected ray

19. Find the distance between the 3rd
images in the two mirrors
a
b

20. A light bulb is placed between two plane mirrors
inclined at an angle of 60o
The number of images
formed are
5
1
60
360
1
360


















Number of images

21. Images by two inclined plane mirrors :
When two plane mirrors are inclined to each other
at an angle , then number of images (n) formed of
an object which is kept between them.









 1
360

o
n


o
360
even integer
(i) If


o
360
odd integer then there are two possibilities
(ii) If







 1
360

n

360

n

25. 1. Two vertical plane mirrors are inclined at an angle of
60o
with each other. A ray of light travelling
horizontally is reflected first from one mirror and then
from the other. The resultant deviation is
o
240
)
60
2
360
(
)
2
360
( 




 


26. 13. A ray of light is incident at 50° on the middle of one of
the two mirrors arranged at an angle of 60° between
them. The ray then touches the second mirror, get
reflected back to the first mirror, making an angle of
incidence of
(a) 50° (b) 60° (c) 70° (d) 80°

In  ABC;  = 180° – (60° + 40°) = 80°
  = 90° – 80° = 10°
In  ABD; A = 60°, B = ( + 2)
= (80 + 2  10) = 100° and D = (90° – )
A + B + D =180°
60° + 100° + (90° – ) = 180°
  = 70°

27. Relation between velocity of the object and image

31. Curved mirrors
Curved mirrors
It is a part of a transparent hollow sphere whose one
surface is polished.
Concave mirror converges the light rays and used as a
shaving mirror, In search light, in cinema projector, in
telescope, by E.N.T. specialists etc.
Convex mirror diverges the light rays and used in road
lamps, side mirror in vehicles etc.

32. Terminology
(i) Pole (P) : Mid point of the mirror
(ii) Centre of curvature (C) : Centre of the sphere of
which
the mirror is a part.
(iii) Radius of curvature (R): Distance between pole and
centre of curvature.
(Rconcave = –ve , Rconvex = +ve , Rplane = )
(iv) Principle axis : A line passing through P and C.
(v) Focus (F) : An image point on principle axis for an
object at .
(vi) Focal length (f) : Distance between P and F.
(vii) Relation between f and R : f=R/2
(fconcave = –ve , fconvex = + ve , fplane =  )
(viii) Power : The converging or diverging ability of
mirror
(ix) Aperture : Effective diameter of light reflecting
area.

33. Curved mirrors
Curved mirrors
• What if the mirror isn’t flat?
What if the mirror isn’t flat?
– light still follows the same rules, with local surface normal
• Parabolic mirrors have exact focus
Parabolic mirrors have exact focus
– used in telescopes, backyard satellite dishes, etc.
– also forms virtual image

34. Concave Mirrors
Concave Mirrors
•Curves inward
•May be real or virtual image
82a425d7
0
0

35. When object is placed at infinite (i.e. u = )
At F
Real
Inverted
Very small in size
Magnification m << – 1
F

36. For a real object close to the mirror but outside
of the center of curvature, the real image is
formed between C and f. The image is inverted
and smaller than the object.
Between F and C
Real
Inverted
Small in size
m < – 1

37. For a real object at C, the real image is
formed at C. The image is inverted and the
same size as the object.
At C
Real
Inverted
Equal in size
m = – 1

38. For a real object between C and f, a real image
is formed outside of C. The image is inverted
and larger than the object.
Between 2f and 
Real
Inverted
Large in size
m > – 1

39. For a real object at f, no image is formed. The
reflected rays are parallel and never converge.
At 
Real
Inverted
Very large in size
m >> – 1

40. For a real object between f and the mirror, a
For a real object between f and the mirror, a
virtual image is formed behind the mirror. The
virtual image is formed behind the mirror. The
image is upright and larger than the object.
image is upright and larger than the object.
Behind the
mirror
Virtual
Erect
Large in size
m > + 1

41. Convex
Convex Mirrors
Mirrors
•Curves outward
•Reduces images
•Virtual images
–Use: Rear view mirrors, store
security…
CAUTION! Objects are closer than they
appear!

42. Convex mirror : Image formed by convex mirror is
always virtual, erect and smaller in size.
(1) When object is placed at infinite (i.e. u = )
Ima
ge
At F
Virtual
Erect
Very small in size
Magnification m <<
+ 1

43. (2) When object is placed any where on the principal
axis
Ima
ge
Between P and F
Virtual
Erect
Small in size
Magnification m <
+ 1

45. MIRROR FORMULA

46. Linear magnification (m)
The ratio of the height of the
image to that of the object is
called linear or transverse
magnification or just
magnification

47. (1) Mirror
formula : u
v
f
1
1
1


(2) Lateral magnification : When an object is placed
perpendicular to the principle axis, then linear
magnification is called lateral or transverse magnification.
f
v
f
u
f
f
u
v
O
I
m







Axial magnification : When object lies along the
principle axis then its axial magnification
)
(
)
(
1
2
1
2
u
u
v
v
O
I
m





If object is small;
2









u
v
du
dv
m
2
2







 











f
v
f
u
f
f

48. Areal magnification : If a 2D-object is placed with
it's plane perpendicular to principle axis. It's Areal
magnification
)
(
object
of
Area
)
(
image
of
Area
o
i
s
A
A
m 
o
i
s
A
A
m
m 

 2

49. An object is placed 10cm in front of a concave mirror of
radius of curvature 15 cm Find the position, nature and
magnification of the image in each case.

50. An object is placed 5 cm in front of a concave mirror of
radius of curvature 15 cm Find the position, nature and
magnification of the image in each case.

51. An object is placed exactly midway between a concave
mirror of radius of curvature 40 cm and a convex mirror of
radius of curvature 30 cm The mirrors face each other and
are 50 cm apart. Determine the nature and position of the
image formed by successive reflections first at the concave
mirror and then at the convex mirror.
(i) For concave mirror.

53. If you sit in a parked car, you glance in the rear view mirror
R= 2 m and notice a jogger approaching. If the jogger is
running at a speed of 5 ms-1
, how fast is the image of the
jogger moving when the jogger is 39 m away ?