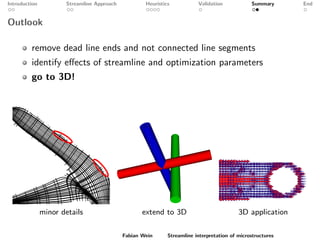
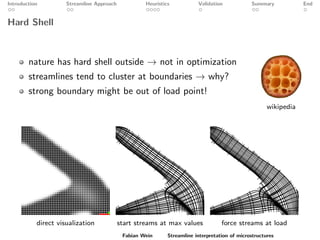
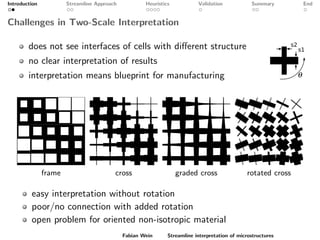
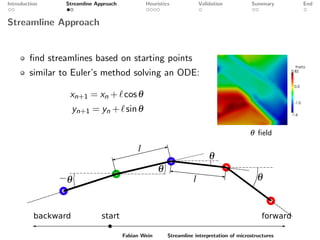
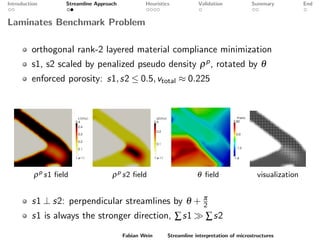
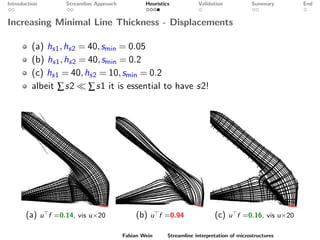
The document discusses a streamline approach to interpret optimized two-scale microstructures for manufacturing. It generates streamlines based on a material density field to represent oriented material distributions. Several heuristics are explored to control the line thickness and density. Numerical validation shows the approach can achieve similar compliance as homogenization while allowing control over manufacturing features. Further work is needed to improve local density control and extend the method to 3D microstructures.

1. Introduction Streamline Approach Heuristics Validation Summary End
Interpretation of local oriented microstructures by a
streamline approach to obtain manufact. structures
F. Wein, J. Greifenstein, Th. Guess, M. Stingl
Applied Mathematics, University Erlangen-Nuremberg, Germany
OPT-i
June 4-6, 2014
Fabian Wein Streamline interpretation of microstructures

2. Introduction Streamline Approach Heuristics Validation Summary End
The Founding Papers in Topology Optimization
Bendsøe & Kikuchi; 1988; Generating optimal topologies in
optimal design using a homogenization method (3281 cites)
homogenized material [c] = H(s1,s2,θ)
two-scale approach
see also talk by Th. Guess, M. Stingl, F. Wein
s2
s1
Bendsøe; 1989; Optimal shape design as a material distribution
problem (1375 cites)
single variable ρ scales homogeneous material
→ Solid Isotropic Material with Penalization
Fabian Wein Streamline interpretation of microstructures

3. Introduction Streamline Approach Heuristics Validation Summary End
Challenges in Two-Scale Interpretation
does not see interfaces of cells with different structure
no clear interpretation of results
interpretation means blueprint for manufacturing
s2
s1
frame cross graded cross rotated cross
easy interpretation without rotation
poor/no connection with added rotation
open problem for oriented non-isotropic material
Fabian Wein Streamline interpretation of microstructures

4. Introduction Streamline Approach Heuristics Validation Summary End
Streamline Approach
find streamlines based on starting points
similar to Euler’s method solving an ODE:
xn+1 = xn + cosθ
yn+1 = yn + sinθ
θ field
start forwardbackward
Fabian Wein Streamline interpretation of microstructures

5. Introduction Streamline Approach Heuristics Validation Summary End
Laminates Benchmark Problem
orthogonal rank-2 layered material compliance minimization
s1, s2 scaled by penalized pseudo density ρp, rotated by θ
enforced porosity: s1,s2 ≤ 0.5,vtotal ≈ 0.225
ρp s1 field ρp s2 field θ field visualization
s1 ⊥ s2: perpendicular streamlines by θ + π
2
s1 is always the stronger direction, ∑s1 ∑s2
Fabian Wein Streamline interpretation of microstructures

6. Introduction Streamline Approach Heuristics Validation Summary End
Applying the Streamline Approach
color coding: given parameter and calculated parameter
start streamlines for s1 and s2 in every cell center
(a) c = 1 → vtotal = 0.89 (b) c = 0.001 → vtotal = 0.82 (c) c s ≥ smin | vtotal = 0.25
(a) streamlines tend to overlap to dense bundles → undesired solid
(b) minimal drawn line thickness is one pixel → too heavy void
(c) → define minimal line stiffness smin, find scaling c to satisfy vtotal
Fabian Wein Streamline interpretation of microstructures

7. Introduction Streamline Approach Heuristics Validation Summary End
Indirect Control of Line Thickness
many lines force strong downscaling to meet volume → thin lines
evaluate data on virtual grid hs, here 20×20
Algorithm to reduce number of lines
start line in virtual cell only with tmax lines → sort lines!
still arbitrary many lines can traverse virtual cells
tmax = ∞ → c = 0.0011 tmax = 5 → c = 0.015 tmax = 1 → c = 0.32
Fabian Wein Streamline interpretation of microstructures

8. Introduction Streamline Approach Heuristics Validation Summary End
Increasing Minimal Line Thickness
s1 s2 in given example → s2 only expressed by thin lines
assume we do not want too thin lines for manufacturing
too restrictive minimal thickness smin eliminates s2
→ separate virtual grid spacing hs1 and hs2
hs1,hs2 = 40,smin = 0.05 hs1,hs2 = 40,smin = 0.2 hs1 = 40,hs2 = 10,smin = 0.2
Fabian Wein Streamline interpretation of microstructures

9. Introduction Streamline Approach Heuristics Validation Summary End
Increasing Minimal Line Thickness - Displacements
(a) hs1,hs2 = 40,smin = 0.05
(b) hs1,hs2 = 40,smin = 0.2
(c) hs1 = 40,hs2 = 10,smin = 0.2
albeit ∑s2 ∑s1 it is essential to have s2!
(a) u f =0.14, vis u×20 (b) u f =0.94 (c) u f =0.16, vis u×20
Fabian Wein Streamline interpretation of microstructures

10. Introduction Streamline Approach Heuristics Validation Summary End
Numerical Validation - Parameter Study
vary hs2 ∈ [10,40] and smin ∈ [0.01,0.2] → image → mesh → FEM
fixed hs1 = 40 and tmax = 2
10
20
30
40 0.0
0.1
0.2
0.210
0.215
0.220
0.225
0.230
vtotal
hs2
smin
vtotal
10
20
30
40 0.0
0.1
0.2
1.0
2.0
3.0
4.0
5.0 u
T
f
hs2
smin
u
T
f
minimal too low: many thin lines → vtotal cannot be reached
minimal too high: loose information → poor compliance
u f : homogenized=1.51, streamline ≈ 1.55 . . . 2.0, SIMP=1.13
Fabian Wein Streamline interpretation of microstructures

11. Introduction Streamline Approach Heuristics Validation Summary End
Summary
Pros
the streamline approach can interpret oriented 2D two-scale results!
performance of interpretation is “close” to homogenized performance
full control of local line thickness
correct orientation of lines (including relative angle)
Cons
poor control of local line density/ local porosity
interpretation is relatively far away from optimized design
problem specific hand tuned heuristics (hs1, hs2, smin, tmax, c)
Fabian Wein Streamline interpretation of microstructures

12. Introduction Streamline Approach Heuristics Validation Summary End
Outlook
remove dead line ends and not connected line segments
identify effects of streamline and optimization parameters
go to 3D!
minor details extend to 3D 3D application
Fabian Wein Streamline interpretation of microstructures

13. Introduction Streamline Approach Heuristics Validation Summary End
thank you for your attention!
Fabian Wein Streamline interpretation of microstructures

14. Introduction Streamline Approach Heuristics Validation Summary End
Hard Shell
nature has hard shell outside → not in optimization
streamlines tend to cluster at boundaries → why?
strong boundary might be out of load point!
wikipedia
direct visualization start streams at max values force streams at load
Fabian Wein Streamline interpretation of microstructures

15. Introduction Streamline Approach Heuristics Validation Summary End
Impact of Macroscopic Optimization Regularization
optimization with different regularization for s1,s2 and θ
(a) low regularization (b) med regularization (c) strong regularization
u f (hom/eval): (a) (1.36/1.51), (b) (1.40,1.50), (c) (1.51,1.66)
apparently streamline have own regularization (hs1 = 40,hs2 = 10)
Fabian Wein Streamline interpretation of microstructures