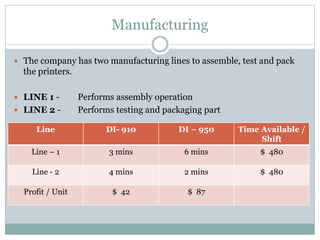
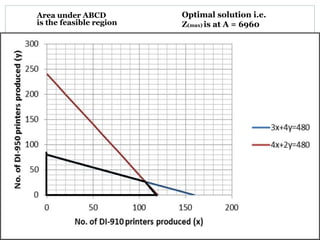
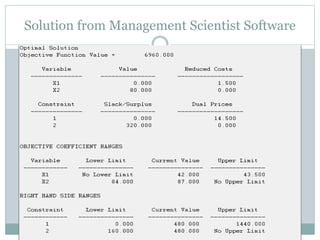
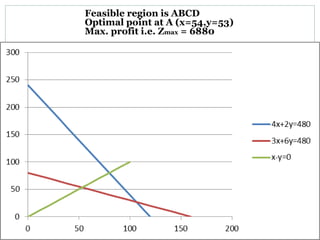
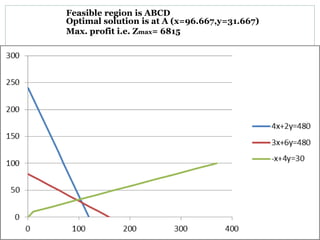
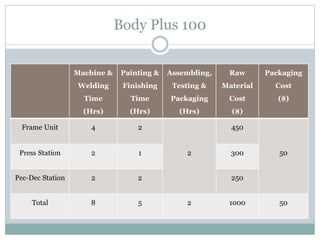
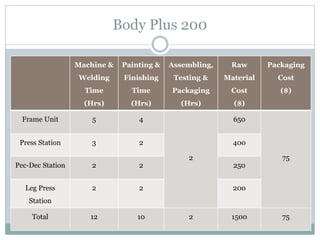
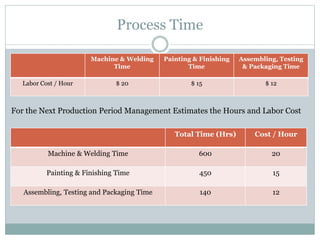
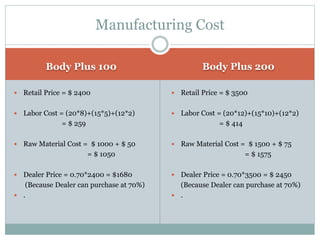
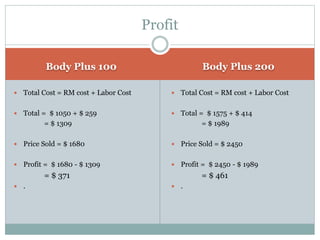
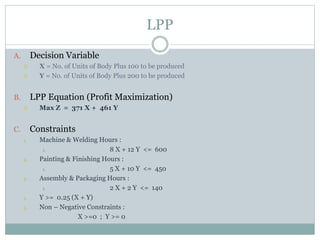
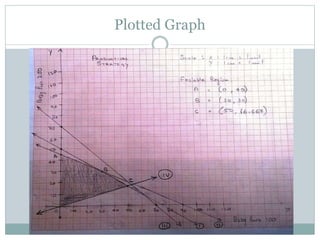
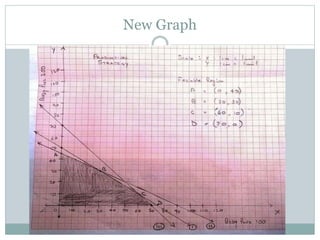
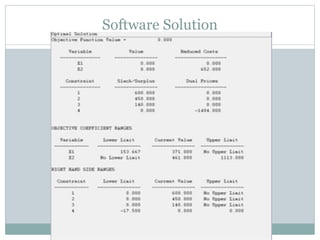
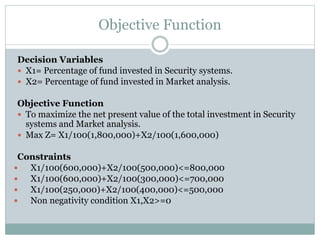
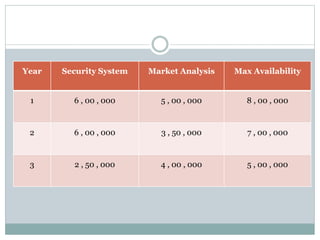
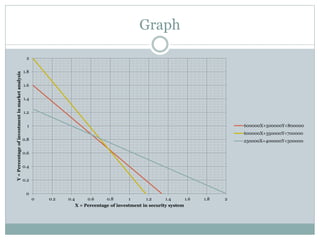
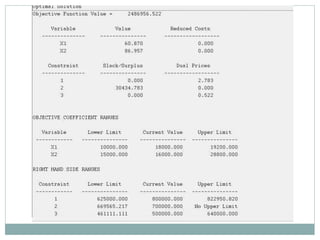
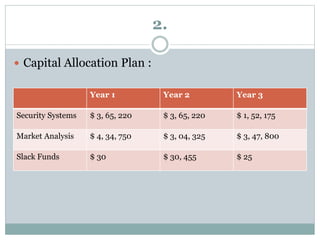
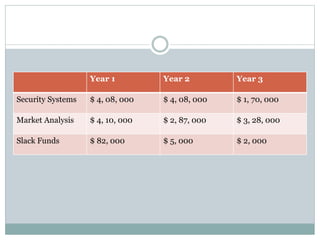
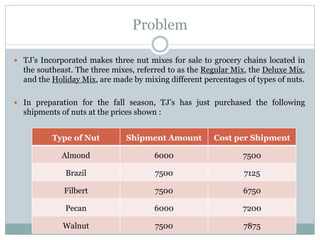
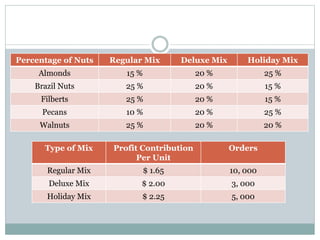
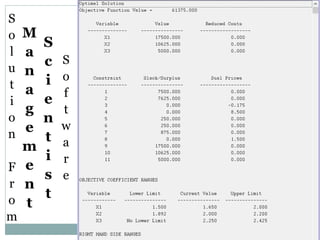
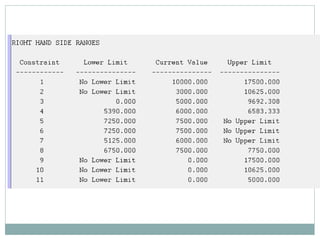
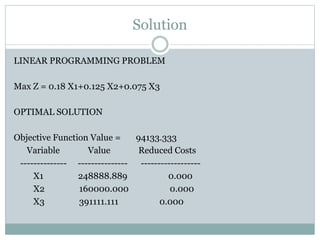
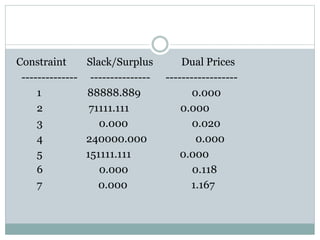
The document discusses operational research case studies for several companies including Digital Imaging which produces photo printers, Better Fitness Inc. that manufactures exercise equipment, and Hart Venture Capital which provides funding for software development projects. The case studies formulate linear programming problems to optimize objectives like profit maximization based on production constraints like available machine time and labor costs.

1. Operational Research
Brenda Gaytan
CASE STUDY
1. Workload Balancing
2. Production Strategy
3. Hart Venture Capital
4. Product Mix
5. Investment Strategy

2. DIGITAL IMAGING (DI)
PHOTO PRINTERS
( A N I N T R O D U C T I O N T O M A N A G E M E N T S C I E N C E )
P G : 8 4 - 8 5
WORKLOAD BALANCING

3. DI Printers
 Digital Imaging (DI) produces photo printers for both
professional and consumer markets. The company recently
introduced two new models of color photo printers namely
DI-910 model and DI-950 model.
Features DI- 910 DI – 950
Photo Size 4” * 6” Borderless 13” * 19” Borderless
Time Taken / Print 37 seconds Faster than DI-910
Profit / Unit $ 42 $ 87

4. Manufacturing
 The company has two manufacturing lines to assemble, test and pack
the printers.
 LINE 1 - Performs assembly operation
 LINE 2 - Performs testing and packaging part
Line DI- 910 DI – 950 Time Available /
Shift
Line – 1 3 mins 6 mins $ 480
Line - 2 4 mins 2 mins $ 480
Profit / Unit $ 42 $ 87

5. Objective Functions
 Decision Variables
Let, X - Number of units of DI-910 model produced in each shift.
Let, Y - Number of units of DI-950 model produced in each shift.
 Objective
The company’s objective is to maximize its profit from overall
production.
 Objective Function
Z (Max.) = 42(X) + 87(Y)

6. Constraints
 Subject To :
For Line 1
3X + 6Y <= 480
For Line 2
4X + 2Y <= 480
Non-Negativity Constraints
X >= 0
Y >= 0

7. 1 (a).
Recommended number of units of each printer to be produced to maximize
the profit :
No. of DI-910 model printers to be produced i.e. X = 0
No. of DI-950 model printers to be produced i.e. Y = 80
Z(Max.) = 42 (0) * 87 (80)  6960
 Now while producing 80 DI-950 printers :
Time used in Assembly Line = 6 X 80 = 480 minutes
Time used in Testing & Packaging = 2 X 80 = 160 minutes
 Time i.e. not utilised in Testing & Packaging = 480 – 160 = 320
minutes
 Line -2 i.e. Testing & Packaging is Idle for 320 minutes/shift

8. Area under ABCD
is the feasible region
Optimal solution i.e.
Z(max) is at A = 6960

9. (b).
Possible reasons for not implementing the recommendation :
Thus, management may not be manufacturing only DI-
950 model printers as :
 Resources on Line 2 will not be utilized fully as there will be an
idle time of 320 minutes (more than half of the total time of the
shift).
 Production/Supply of DI-950 model printers may be in excess of
market demand.
 Demand of DI-910 model printers will be left unfulfilled.

10. Solution from Management Scientist Software

11. 2.
DI Company wants to produce as many DI-910
model printers as DI-950 model printers :
 Now in this case, a new constraint will further be added to the original
problem :
X >= Y, or
X – Y >= 0
We will achieve our optimal point at :
X = 53.33
Y = 53.33
But since production of printers can not be done in this way,
the company would produce :
X = 54
Y = 53
Z(Max.) = 42 (54) * 87 (53)  6880

12. Feasible region is ABCD
Optimal point at A (x=54,y=53)
Max. profit i.e. Zmax = 6880

13. Solution from Management Scientist Software

14. 3.
Analysis of resource utilization on Line 1 and Line 2 in reference to
solution developed in part (2) :
Time used in Assembly line = (3 X 54) + (6 X 53) = 480
minutes
Time used in Testing & Packaging = (4 X 54) + (2 X 53) = 322
minutes
 Time i.e. not utilized in Testing & Packaging =
480 – 322 = 158 minutes
Now as there is a lot of time in Line 2 still unused, the main
concern for the company would be how to utilize this unused
time in a productive manner so that it add value to the
company as well as its profits.

15. 4.
Management wants to limit the time difference between both the lines
by 30 minutes or less :
In this case, a new constraint will be added to the original problem :
(3X + 6Y ) – (4X + 2Y) <= 30, or
- X + 4Y <= 30
 Through Management Scientist Software, the new calculated values will
be :
X = 96.667
Y = 31.667
Z(Max.) = 42(96.667) + 87(31.667)  6815
 Time consumed in Line 1 = (3 X 96.667) + (6 X 31.667) = 480 minutes
 Time consumed in Line-2 = (4 X 96.667) + (2 X 31.667) = 450 minutes
Time Difference = 480 – 450  30 minutes

16. Solution from Management Scientist Software

17. Feasible region is ABCD
Optimal solution is at A (x=96.667,y=31.667)
Max. profit i.e. Zmax= 6815

18.  Now again since the production of printers can not be
done in this way, the company would produce :
X = 98
Y = 31
Z(Max.) = 42 (98) * 87 (31)  6813
 Time consumed in Line 1 = (3 X 98) + (6 X 31) = 480 minutes
 Time consumed in Line-2 = (4 X 98) + (2 X 31) = 454 minutes
Time Difference = 480 – 454  26 minutes

19. 5.
Objective is to maximize the number of printers
produced :
Since the objective of the company has changed from maximizing profits to maximizing
production, the objective function would also change :
New Objective Function :
Z(Max.) = X + Y
 Through Management Scientist Software, the new calculated values will
be :
X = 106.227
Y = 26.667
For convenience in production, the company would produce :
X = 106
Y = 27
Z(Max.) = 42 (106) * 87 (26)  6801
 Time consumed in line-1 = (3 X 106) + (6 X 27) = 480 minutes
 Time consumed in line-2 = (4 X 106) + (2 X 27) = 478 minutes

20. Solution from Management Scientist Software

21. BETTER FITNESS INC. (BFI)
EXERCISE EQUIPMENT MANUFACTURING
( A N I N T R O D U C T I O N T O M A N A G E M E N T S C I E N C E )
P G : 8 5 - 8 6
PRODUCTION STRATEGY

22. Components of Machines
Two machines are to be Manufactured :
 Body Plus 100
1. Frame Unit
2. Press Station
3. Pec-Dec Station
 Body Plus 200
1. Frame Unit
2. Press Station
3. Pec-Dec Station
4. Leg Press Station

23. Activities Involved in Manufacturing
 There are various activities involved in per unit
manufacturing of ‘Body Plus 100’ and ‘Body Plus 200’ :
 Machining and Welding
 Painting and Finishing
 Assembling, Packaging and Testing
 Three of these activities take separate time for both the
machines

24. Body Plus 100
Machine &
Welding
Time
(Hrs)
Painting &
Finishing
Time
(Hrs)
Assembling,
Testing &
Packaging
(Hrs)
Raw
Material
Cost
($)
Packaging
Cost
($)
Frame Unit 4 2
2
450
50Press Station 2 1 300
Pec-Dec Station 2 2 250
Total 8 5 2 1000 50

25. Body Plus 200
Machine &
Welding
Time
(Hrs)
Painting &
Finishing
Time
(Hrs)
Assembling,
Testing &
Packaging
(Hrs)
Raw
Material
Cost
($)
Packaging
Cost
($)
Frame Unit 5 4
2
650
75
Press Station 3 2 400
Pec-Dec Station 2 2 250
Leg Press
Station
2 2 200
Total 12 10 2 1500 75

26. Process Time
Machine & Welding
Time
Painting & Finishing
Time
Assembling, Testing
& Packaging Time
Labor Cost / Hour $ 20 $ 15 $ 12
Total Time (Hrs) Cost / Hour
Machine & Welding Time 600 20
Painting & Finishing Time 450 15
Assembling, Testing and Packaging Time 140 12
For the Next Production Period Management Estimates the Hours and Labor Cost

27. Body Plus 100 Body Plus 200
 Retail Price = $ 2400
 Labor Cost = (20*8)+(15*5)+(12*2)
= $ 259
 Raw Material Cost = $ 1000 + $ 50
= $ 1050
 Dealer Price = 0.70*2400 = $1680
(Because Dealer can purchase at 70%)
 .
 Retail Price = $ 3500
 Labor Cost = (20*12)+(15*10)+(12*2)
= $ 414
 Raw Material Cost = $ 1500 + $ 75
= $ 1575
 Dealer Price = 0.70*3500 = $ 2450
(Because Dealer can purchase at 70%)
 .
Manufacturing Cost

28. Body Plus 100 Body Plus 200
 Total Cost = RM cost + Labor Cost
 Total = $ 1050 + $ 259
= $ 1309
 Price Sold = $ 1680
 Profit = $ 1680 - $ 1309
= $ 371
 .
 Total Cost = RM cost + Labor Cost
 Total = $ 1575 + $ 414
= $ 1989
 Price Sold = $ 2450
 Profit = $ 2450 - $ 1989
= $ 461
 .
Profit

29. LPP
A. Decision Variable
 X = No. of Units of Body Plus 100 to be produced
 Y = No. of Units of Body Plus 200 to be produced
B. LPP Equation (Profit Maximization)
 Max Z = 371 X + 461 Y
C. Constraints
1. Machine & Welding Hours :
1. 8 X + 12 Y <= 600
2. Painting & Finishing Hours :
1. 5 X + 10 Y <= 450
3. Assembly & Packaging Hours :
1. 2 X + 2 Y <= 140
4. Y >= 0.25 (X + Y)
5. Non – Negative Constraints :
X >=0 ; Y >= 0

30. Plotted Graph

31. 1.
 The Optimal Solution is from one among the Feasible region points
 Hence, the recommended number of machines are :
 Body Plus 100 = 50
 Body Plus 200 = 16
Points Max Z Solution
A 0 , 45
Z = 371 X + 461 Y
20,745
B 30 , 30 24,960
C 50 , 16.667 26,233.48 Optimal Solution

32. 2.
 If the constraint of “producing atleast 25% of Body Plus 200” is
removed.
 Then the graph shall be plotted for the following constraints:
1. Machine & Welding Hours :
1. 8 X + 12 Y <= 600
2. Painting & Finishing Hours :
1. 5 X + 10 Y <= 450
3. Assembly & Packaging Hours :
1. 2 X + 2 Y <= 140
4. Non – Negative Constraints :
X >=0 ; Y >= 0

33. New Graph

34. New Solution
 The Optimal Solution is from one among the Feasible region points
 Hence, the recommended number of machines are :
 Body Plus 100 = 60
 Body Plus 200 = 10
 The Profit Margin Increases by
= $ 26,870 - $ 26,233.48
= $ 636.52
Points Max Z Solution
A 0 , 45
Z = 371 X + 461 Y
20,745
B 30 , 30 24,960
C 60 , 10 26,870
D 70 , 0 25,970
Optimal Solution

35. 3.
 We can see that the “Upper Limit” in ‘X’ is not fixed, whereas in ‘Y’ it is
1113 units
 When looking at the Objective function Coefficient ranges we see that
the objective function yields maximum profits (1113 units) by selling
only Body Plus 200.
 Also, the reduced costs of manufacturing only Body Plus 200 is 652.
 Therefore, the efforts should be expended, in Body Plus 200 to yield
maximum profit.

36. Software Solution

37. HART VENTURE CAPITAL (HVC)
VENTURE CAPITAL FOR SOFTWARE
DEVELOPMENT
( A N I N T R O D U C T I O N T O M A N A G E M E N T S C I E N C E )
P G : 8 6 - 8 7
HART VENTURE CAPITAL

38. Objective Function
Decision Variables
 X1= Percentage of fund invested in Security systems.
 X2= Percentage of fund invested in Market analysis.
Objective Function
 To maximize the net present value of the total investment in Security
systems and Market analysis.
 Max Z= X1/100(1,800,000)+X2/100(1,600,000)
Constraints
 X1/100(600,000)+X2/100(500,000)<=800,000
 X1/100(600,000)+X2/100(300,000)<=700,000
 X1/100(250,000)+X2/100(400,000)<=500,000
 Non negativity condition X1,X2>=0

39. Year Security System Market Analysis Max Availability
1 6 , 00 , 000 5 , 00 , 000 8 , 00 , 000
2 6 , 00 , 000 3 , 50 , 000 7 , 00 , 000
3 2 , 50 , 000 4 , 00 , 000 5 , 00 , 000

40. Graph
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Y=Percentageofinvestmentinmarketanalysis
X = Percentage of investment in security system
600000X+500000Y<800000
600000X+350000Y<700000
250000X+400000Y<500000

42. 1.
 HVC should invest 60.87% in Security systems and 86.95%
in Market analysis.
 Net present value of total investment is $2,486,956.522

43. 2.
 Capital Allocation Plan :
Year 1 Year 2 Year 3
Security Systems $ 3, 65, 220 $ 3, 65, 220 $ 1, 52, 175
Market Analysis $ 4, 34, 750 $ 3, 04, 325 $ 3, 47, 800
Slack Funds $ 30 $ 30, 455 $ 25

44. 3.
 Assuming that the additional $100000 is made available to
HVC to be invested in any year.
 HVC should choose to invest these funds in these
proportions in the two projects
 The following effects will take place :
A. % invested funded for Security Systems will become 68%
B. % invested funded for Market Analysis will become 82%
C. Net Present Value will become $2536000.

45. Year 1 Year 2 Year 3
Security Systems $ 4, 08, 000 $ 4, 08, 000 $ 1, 70, 000
Market Analysis $ 4, 10, 000 $ 2, 87, 000 $ 3, 28, 000
Slack Funds $ 82, 000 $ 5, 000 $ 2, 000

46. 4.
 Assuming the additional $100000 is committed for
the first year itself, the capital allocation plan is
 For Security systems:
1. Year 1 = $413,112
2. Year 2 = $413,112
3. Year 2 = $172,130
 For market analysis:
1. Year 1 = $409,835
2. Year 2 = $286,884
3. Year 2 = $327,868

47. 5.
 As we saw, when an additional $100000 is invested,
the net present value goes up by $49140 with a slack
of $89000. These slack funds may be reinvested in
lucrative options available with HVC.

48. TJ’S INC.
NUT MIXES FOR SALE TO GROCERY
CHAINS
( A N I N T R O D U C T I O N T O M A N A G E M E N T S C I E N C E )
P G : 1 5 1 - 1 5 2
PRODUCT MIX

49. Problem
 TJ’s Incorporated makes three nut mixes for sale to grocery chains located in
the southeast. The three mixes, referred to as the Regular Mix, the Deluxe Mix,
and the Holiday Mix, are made by mixing different percentages of types of nuts.
 In preparation for the fall season, TJ’s has just purchased the following
shipments of nuts at the prices shown :
Type of Nut Shipment Amount Cost per Shipment
Almond 6000 7500
Brazil 7500 7125
Filbert 7500 6750
Pecan 6000 7200
Walnut 7500 7875

50. Percentage of Nuts Regular Mix Deluxe Mix Holiday Mix
Almonds 15 % 20 % 25 %
Brazil Nuts 25 % 20 % 15 %
Filberts 25 % 20 % 15 %
Pecans 10 % 20 % 25 %
Walnuts 25 % 20 % 20 %
Type of Mix Profit Contribution
Per Unit
Orders
Regular Mix $ 1.65 10, 000
Deluxe Mix $ 2.00 3, 000
Holiday Mix $ 2.25 5, 000

51. Managerial Report
Perform an analysis of TJ’s product mix problem, and prepare a report for
TJ’s president that summarizes your finding. Be sure to include
information and analysis on the following:
1. The cost per pound of the nuts included in the Regular, Deluxe, and
Holiday mixes.
2. The optimal product mix and the total profit contribution.
3. Recommendations regarding how the total profit contribution can be
increased if additional quantities of nuts can be purchased.
4. A recommendation as to whether TJ’s should purchase an additional
1,000 pounds of almonds for $1,000 from a supplier who overbought.
5. Recommendations on how profit contribution could be increased (if
at all) if TJ’s does not satisfy all existing orders.

52. L.P.P Formulation
Decision variables :
 R = pounds of Regular Mix
 D = pounds of Deluxe Mix
 H = pounds of Holiday Mix
Objective function :
 Z = 1.65R + 2.00D + 2.25H - 36450

53. Constraints
 R > 10000
 D > 3000
 H > 5000
 .15R + .20D + .25H < 6000
 .15R + .20D + .15H < 7500
 .15R + .20D + .15H < 7500
 .10R + .20D + .25H < 6000
 .25R + .20D + .20H < 7500
 R, D, H > 0

54. S
o
l
u
t
i
o
n
F
r
o
m
M
a
n
a
g
e
m
e
n
t
S
c
i
e
n
t
i
s
t
S
o
f
t
w
a
r
e

56. Interpretation
 The Objective Function Value : optimal solution - maximum profit -
$61375.
 Subtract $36450 from the original Objective Function Value
 Subtract the total cost per shipment of the different nuts,
 Optimal Solution - maximum profits - $24935.
 Optimal decision production = 17500 of regular mix,10625 of deluxe mix,
and 5000 of holiday mix.
 Optimal solution exceeds the customer orders for regular Mix by 7500
pounds
 Optimal solution exceeds the customer orders for deluxe Mix by 7625
pounds
 Holiday mix binding constraint(zero surplus)
 The negative dual price indicates that increasing the customer orders for
Holiday mix from 5000 to 5001 pounds will actually decrease the profit
contribution by $0.18.

57. Recommendations
 Increase the quantity of almonds and walnuts purchased by Tj’s and
increase their profit contribution at rate of $8.5 per pound of almonds
and $1.5 per pound of walnuts.
 No more buying of brazil nuts, filberts and pecans.
 Almonds - For each additional pound purchased the profit would
increase @ $8.5 for 583 pounds.
 Walnuts - For each additional pound purchased the profit would
increase @ $1.5 for 250 pounds.
 Dual price of -.175 for the pounds of holiday mix indicate the desire to
reduce the production of this mix.
 The range of feasibility indicates the need to reduce the customer
orders to zero and the value of reduction @ $.18 per pound.

58. J.D. WILLIAMS INC.
INVESTMENT ADVISORY FIRM
( A N I N T R O D U C T I O N T O M A N A G E M E N T S C I E N C E )
P G : 1 5 2 - 1 5 3
INVESTMENT STRATEGY

59. Objective Function
The Case talks about an Investment Advisory firm having more than $120
million of funds with numerous clients.
The problem at hand is about an $800,000 new investment which is to be
invested in three portfolios
Therefore
Decision Variables:
X1=Investment in growth fund
X2=Investment in income fund
X3=Investment in money market fund
Objective Function:
Maximize Z= 0.18X1+0.125X2+0.075X3

60. Constraints
Subject to:
1) -0.8 X1+0.2 X2+0.2 X3<0
2) -0.6 X1+0.4 X2+0.4 X3>0
3) 0.2 X1-0.8 X2+0.2 X3<0
4) 0.5 X1-0.5 X2+0.5 X3>0
5) 0.3 X1+0.3 X2-0.7 X3<0
6) 1 X1+1 X2+1 X3=800000
7) 0.05 X1+0.02 X2-0.04 X3<0

61. Solution
LINEAR PROGRAMMING PROBLEM
Max Z = 0.18 X1+0.125 X2+0.075 X3
OPTIMAL SOLUTION
Objective Function Value = 94133.333
Variable Value Reduced Costs
-------------- --------------- ------------------
X1 248888.889 0.000
X2 160000.000 0.000
X3 391111.111 0.000

62. Constraint Slack/Surplus Dual Prices
-------------- --------------- ------------------
1 88888.889 0.000
2 71111.111 0.000
3 0.000 0.020
4 240000.000 0.000
5 151111.111 0.000
6 0.000 0.118
7 0.000 1.167

63. OBJECTIVE COEFFICIENT RANGES
Variable Lower Limit Current Value Upper Limit
------------ --------------- --------------- ---------------
X1 0.150 0.180 No Upper Limit
X2 No Lower Limit 0.125 0.145
X3 0.015 0.075 0.180
RIGHT HAND SIDE RANGES
Constraint Lower Limit Current Value Upper Limit
------------ --------------- --------------- ---------------
1 -88888.889 0.000 No Upper Limit
2 No Lower Limit 0.000 71111.111
3 -133333.333 0.000 106666.667
4 No Lower Limit 0.000 240000.000
5 -151111.111 0.000 No Upper Limit
6 0.000 800000.000 No Upper Limit
7 -8000.000 0.000 6400.000

64. 1.
From the above solution out of 800,000 the
investment should be as follows:
Growth Fund: $248888.889
Income Fund: $160000.000
Money Market Fund: $391111.111
The annual growth anticipated from the investment
recommendation is $94133.333

65. 2.
 If the clients risk index increased from 0.05 to 0.055
 The new yield index would increase by $4666.67 to
$98800

66. 3 (a).
If the annual yield for growth fund is decreased to 16% for
Growth then the investment recommendation would be
as follows
Growth fund :$248890; Change: 1.111
Income Fund :$160000; Change: 0
Money Market Fund :$391110 ; Change: 0
The value of yield per year is $89155.650 from $94133.333
with a change of $4977.68

67. 3 (b).
If the annual yield for growth fund is decreased to 14% for
Growth then the investment recommendation would be as
follows
Growth fund :$160000; Change: $88888.889
Income Fund :$293335; Change: $133335
Money Market Fund :$346665 ;Change: $44446.11
The value of yield per year is $85066.750.650 from
$94133.333 with a change of $9066.583

68. 4.
 According to the question there will be an additional constraint added
as:
X1<=X2
i.e., X1-X2<=0
With the following constraints added the investment recommendation
is as follows :
Growth fund :$213334; Change: $35554.889
Income Fund :$213334; Change: $53334
Money Market Fund :$373332; Change: $17779.11
The value of yield per year is $93066.770 from $94133.333 with a change
of $1066.563

69. 5.
 Yes the asset allocation model can be used can be used for
any number of clients as long as the values of
Growth Fund is above 15%
Income Fund is below 14.5%
Money market Fund is in between 1.5% to 18%

70. Bibliography & Reference
 An Introduction to Management Science :
Quantitative Approaches to Decision Making
 The Management Scientist Version 6.0 Software