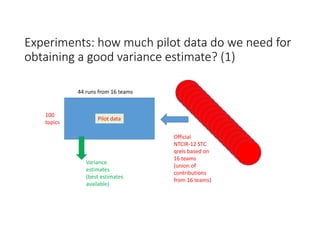
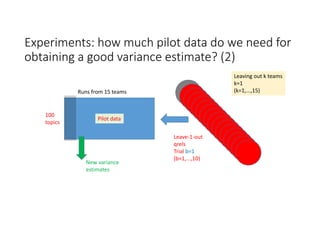
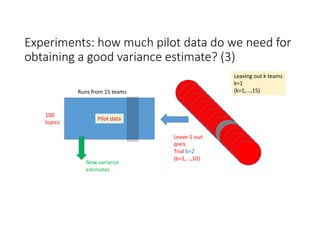
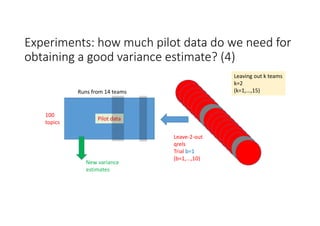
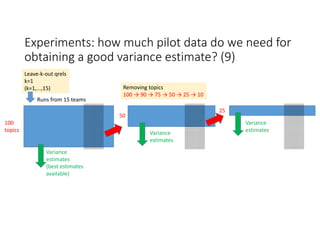
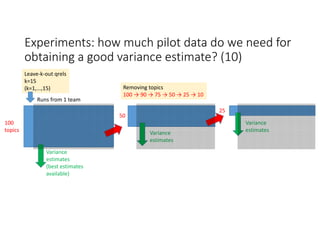
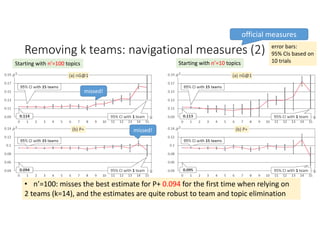
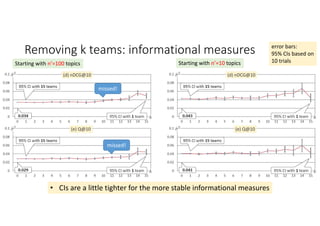
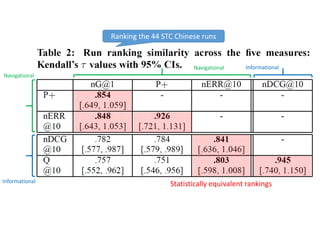
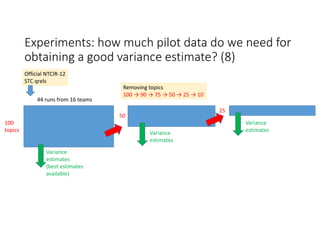
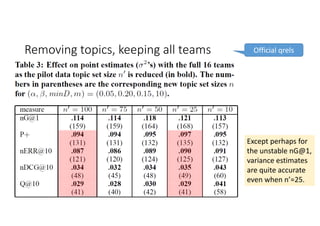
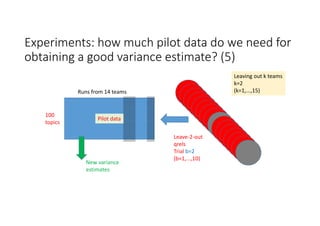
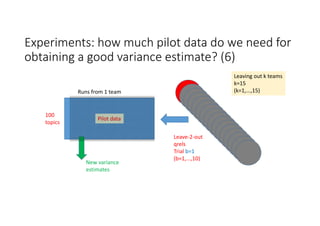
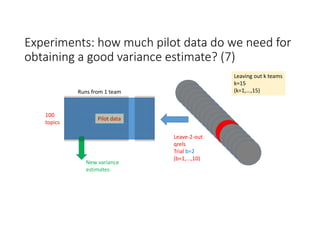
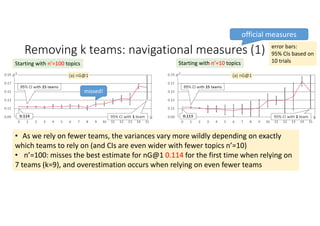
According to experiments using data from the NTCIR-12 STC task: - Variance estimates for evaluation measures were generally accurate even when using as few as 25 topics, provided reasonably stable measures were used. - As fewer teams' data was used to estimate variances, the estimates became more unstable and inaccurate, especially for less stable measures like nG@1. Using data from at least 7-9 teams seemed necessary to obtain reliable estimates. - Variance estimates were more accurate when starting with 100 topics compared to only 10 topics, and informational measures had tighter confidence intervals than navigational measures.

1. On Estimating Variances for
Topic Set Size Design
Tetsuya Sakai Waseda University tetsuyasakai@acm.org
Lifeng Shang Huawei Noah’s Ark Lab shang.lifeng@huawei.com
7th June 2016@EVIA 2016, Tokyo, Japan.

2. TAKEAWAYS
• Topic set size design provides principles and procedures for test
collection builders to decide on the number of topics to create, but
requires a variance estimate for a particular evaluation measure.
• To compute a variance estimate, one needs a topic‐by‐run matrix.
This is inconvenient if we are building a test collection for a new task.
How many topics and teams are required for obtaining a reliable
estimate?
• Answer: According to our experiment with the STC data (100 topics
times 16 teams), about 25 topics with a few teams seems sufficient,
provided reasonably stable measures are used.

3. TALK OUTLINE
1. Topic set size design
2. NTCIR‐12 STC
3. Experiments
4. Conclusions and Future Work

4. I’m building a new test collection. How many
topics should I create?
Target document collection
Topic Relevance assessments
Topic Relevance assessments
Topic Relevance assessments
: :
n ?
Systems will be compared using
sample means of measure M over n topics

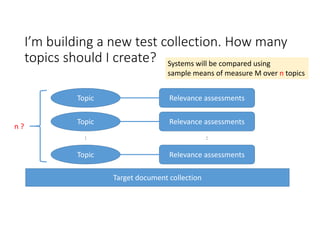
5. Topic set size design [Sakai15IRJ]
http://link.springer.com/content/pdf/10.1007%2Fs10791‐015‐9273‐z.pdf
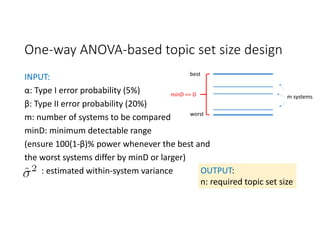
• Set n so as to ensure high statistical power for paired t‐tests
(comparing any two systems with a difference of minDt or larger)
• Set n so as to ensure high statistical power for one‐way ANOVAs
(comparing any m systems with a range of minD or larger)
• Set n so as to ensure the Confidence Interval (CI) of any system difference
is no wider than δ.
open access
Truth
H0 H1
Conclusion H0 Correct (1‐α) Type II Error (β)
H1 Type I Error (α) Correct (1‐β)
Power: ability to detect a
real difference

6. One‐way ANOVA‐based topic set size design
INPUT:
α: Type I error probability (5%)
β: Type II error probability (20%)
m: number of systems to be compared
minD: minimum detectable range
(ensure 100(1‐β)% power whenever the best and
the worst systems differ by minD or larger)
: estimated within‐system variance OUTPUT:
n: required topic set size
m systems
best
worst
minD <= D

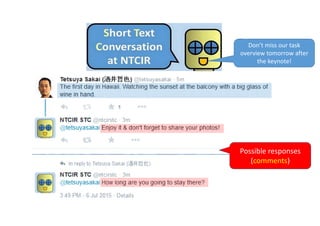
7. Relationships with the other two topic set size
design methods [Sakai15IRJ]
ANOVA‐based results for m=10 can be
used instead of CI‐based results
ANOVA‐based
results for m=2
can be used
instead of t‐test‐
based results

8. Estimating the variance
for an evaluation measure can be estimated easily if we have a
topic‐by‐run matrix from some pilot data.
Sample mean for the i‐th run
Residual variance from one‐way ANOVA
score matrixn’ topics
m’ runs
But how much pilot data do we need before building the actual test collection?

9. TALK OUTLINE
1. Topic set size design
2. NTCIR‐12 STC
3. Experiments
4. Conclusions and Future Work

10. Possible responses
(comments)
Don’t miss our task
overview tomorrow after
the keynote!

11. Given a new post, can the system return a “good” response by
retrieving a comment to an old post from a repository?
old post old comment
old post old comment
old post old comment
old post old comment
old post old comment
new post
new post
new post
old comment
old comment
old comment
new post
new post For each new post,
retrieve and rank
old comments!
Graded label (L0‐L2) for each comment
Repository Training data Test data
Don’t miss our task
overview tomorrow after
the keynote!

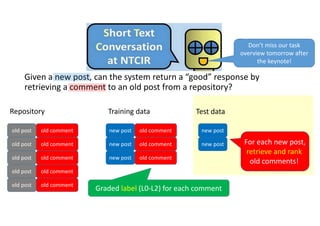
12. STC Chinese subtask evaluation measure:
nG@1 (or nDCG@1 [Jarvelin+02] )
L2‐relevant
L2‐relevant
L1‐relevant
L1‐relevant
1
2
3
4
ideal
ranked list
3 points
3 points
1 points
1 points
L1‐relevant
Nonrelevant
L2‐relevant
Nonrelevant
1
2
3
4
System
output
3 points
1 point
Nonrelevantk
:
nG@1=1/3
nG@1 = 0 or 1/3 or 1
Gain Gain

13. STC Chinese subtask evaluation measure:
P+ [Sakai06AIRS]
L1‐relevant
Nonrelevant
L2‐relevant
Nonrelevant
1
2
3
4
System
output
Nonrelevantk
:
rp : most relevant
in list, nearest to
the top
No user will
go beyond rp
50% of users
50% of users
1 point
3 points
L2‐relevant
L2‐relevant
L1‐relevant
L1‐relevant
1
2
3
4
ideal
ranked list
3 points
3 points
1 point
1 point
Gain Gain
BR(3) = (2 + 4)/(3 + 7) = 0.6
BR(1) = (1 + 1)/(1 + 3) = 0.5
P+ = (BR(1) + BR(3))/ 2 = 0.5500

14. STC Chinese subtask evaluation measures:
nERR@10 [Chapelle11]
L2‐relevant
L2‐relevant
L1‐relevant
L1‐relevant
1
2
3
4
ideal
ranked list
L1‐relevant
Nonrelevant
L2‐relevant
Nonrelevant
1
2
3
4
System
output
Nonrelevantk
:
All users All users
1/4 of users
3/4 of users
3/4 of users
1/4 of users
3/4 of users
3/4 of users
1/4 of users
1/4 of users
1/4 of users
1/4 of users
3/4 of users
3/4 of users
ERR = 0.4375
ERR* = 0.8519
nERR = ERR/ERR* = 0.5136

15. Informational
InformationalNavigational
Navigational
Ranking the 44 STC Chinese runs
Statistically equivalent rankings

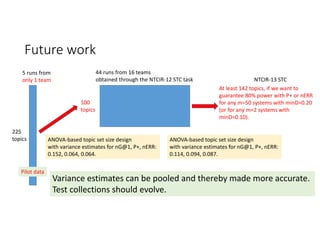
16. STC Chinese subtask: the story so far [Sakai15AIRS]
https://waseda.box.com/AIRS2015
225
topics
5 runs from
only 1 team
100
topics
44 runs from 16 teams
obtained through the NTCIR‐12 STC task
ANOVA‐based topic set size design
with variance estimates for nG@1, P+, nERR:
0.152, 0.064, 0.064.
Pilot data

17. TALK OUTLINE
1. Topic set size design
2. NTCIR‐12 STC
3. Experiments
4. Conclusions and Future Work

18. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (1)
100
topics
44 runs from 16 teams
Pilot data
Variance
estimates
(best estimates
available)
Official
NTCIR‐12 STC
qrels based on
16 teams
(union of
contributions
from 16 teams)

19. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (2)
100
topics
Runs from 15 teams
Pilot data
New variance
estimates
Leave‐1‐out
qrels
Trial b=1
(b=1,...,10)
Leaving out k teams
k=1
(k=1,...,15)

20. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (3)
100
topics
Runs from 15 teams
Pilot data
New variance
estimates
Leave‐1‐out
qrels
Trial b=2
(b=1,...,10)
Leaving out k teams
k=1
(k=1,...,15)

21. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (4)
100
topics
Runs from 14 teams
Pilot data
New variance
estimates
Leave‐2‐out
qrels
Trial b=1
(b=1,...,10)
Leaving out k teams
k=2
(k=1,...,15)

22. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (5)
100
topics
Runs from 14 teams
Pilot data
New variance
estimates
Leave‐2‐out
qrels
Trial b=2
(b=1,...,10)
Leaving out k teams
k=2
(k=1,...,15)

23. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (6)
100
topics
Runs from 1 team
Pilot data
New variance
estimates
Leave‐2‐out
qrels
Trial b=1
(b=1,...,10)
Leaving out k teams
k=15
(k=1,...,15)

24. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (7)
100
topics
Runs from 1 team
Pilot data
New variance
estimates
Leave‐2‐out
qrels
Trial b=2
(b=1,...,10)
Leaving out k teams
k=15
(k=1,...,15)

25. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (8)
100
topics
44 runs from 16 teams
Variance
estimates
(best estimates
available)
50
25
Variance
estimates
Variance
estimates
Removing topics
100 → 90 → 75 → 50 → 25 → 10
Official NTCIR‐12
STC qrels

26. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (9)
100
topics
Runs from 15 teams
Variance
estimates
(best estimates
available)
50
25
Variance
estimates
Variance
estimates
Removing topics
100 → 90 → 75 → 50 → 25 → 10
Leave‐k‐out qrels
k=1
(k=1,...,15)

27. Experiments: how much pilot data do we need for
obtaining a good variance estimate? (10)
100
topics
Runs from 1 team
Variance
estimates
(best estimates
available)
50
25
Variance
estimates
Variance
estimates
Removing topics
100 → 90 → 75 → 50 → 25 → 10
Leave‐k‐out qrels
k=15
(k=1,...,15)

28. Removing topics, keeping all teams Official qrels
Except perhaps for
the unstable nG@1,
variance estimates
are quite accurate
even when n’=25.

29. Removing k teams: navigational measures (1)
official measures
Starting with n’=100 topics Starting with n’=10 topics
error bars:
95% CIs based on
10 trials
• As we rely on fewer teams, the variances vary more wildly depending on exactly
which teams to rely on (and CIs are even wider with fewer topics n’=10)
• n’=100: misses the best estimate for nG@1 0.114 for the first time when relying on
7 teams (k=9), and overestimation occurs when relying on even fewer teams
missed!

30. Removing k teams: navigational measures (2)
official measures
Starting with n’=100 topics Starting with n’=10 topics
error bars:
95% CIs based on
10 trials
• n’=100: misses the best estimate for P+ 0.094 for the first time when relying on
2 teams (k=14), and the estimates are quite robust to team and topic elimination
missed!
missed!

31. Removing k teams: informational measures
Starting with n’=100 topics Starting with n’=10 topics
error bars:
95% CIs based on
10 trials
• CIs are a little tighter for the more stable informational measures
missed!
missed!

32. TALK OUTLINE
1. Topic set size design
2. NTCIR‐12 STC
3. Experiments
4. Conclusions and Future Work

33. TAKEAWAYS AGAIN
• Topic set size design provides principles and procedures for test
collection builders to decide on the number of topics to create, but
requires a variance estimate for a particular evaluation measure.
• To compute a variance estimate, one needs a topic‐by‐run matrix.
This is inconvenient if we are building a test collection for a new task.
How many topics and teams are required for obtaining a reliable
estimate?
• Answer: According to our experiment with the STC data (100 topics
times 16 teams), about 25 topics with a few teams seems sufficient,
provided reasonably stable measures are used.

34. Future work
225
topics
5 runs from
only 1 team
100
topics
44 runs from 16 teams
obtained through the NTCIR‐12 STC task
ANOVA‐based topic set size design
with variance estimates for nG@1, P+, nERR:
0.152, 0.064, 0.064.
Pilot data
NTCIR‐13 STC
ANOVA‐based topic set size design
with variance estimates for nG@1, P+, nERR:
0.114, 0.094, 0.087.
At least 142 topics, if we want to
guarantee 80% power with P+ or nERR
for any m=50 systems with minD=0.20
(or for any m=2 systems with
minD=0.10).
Variance estimates can be pooled and thereby made more accurate.
Test collections should evolve.