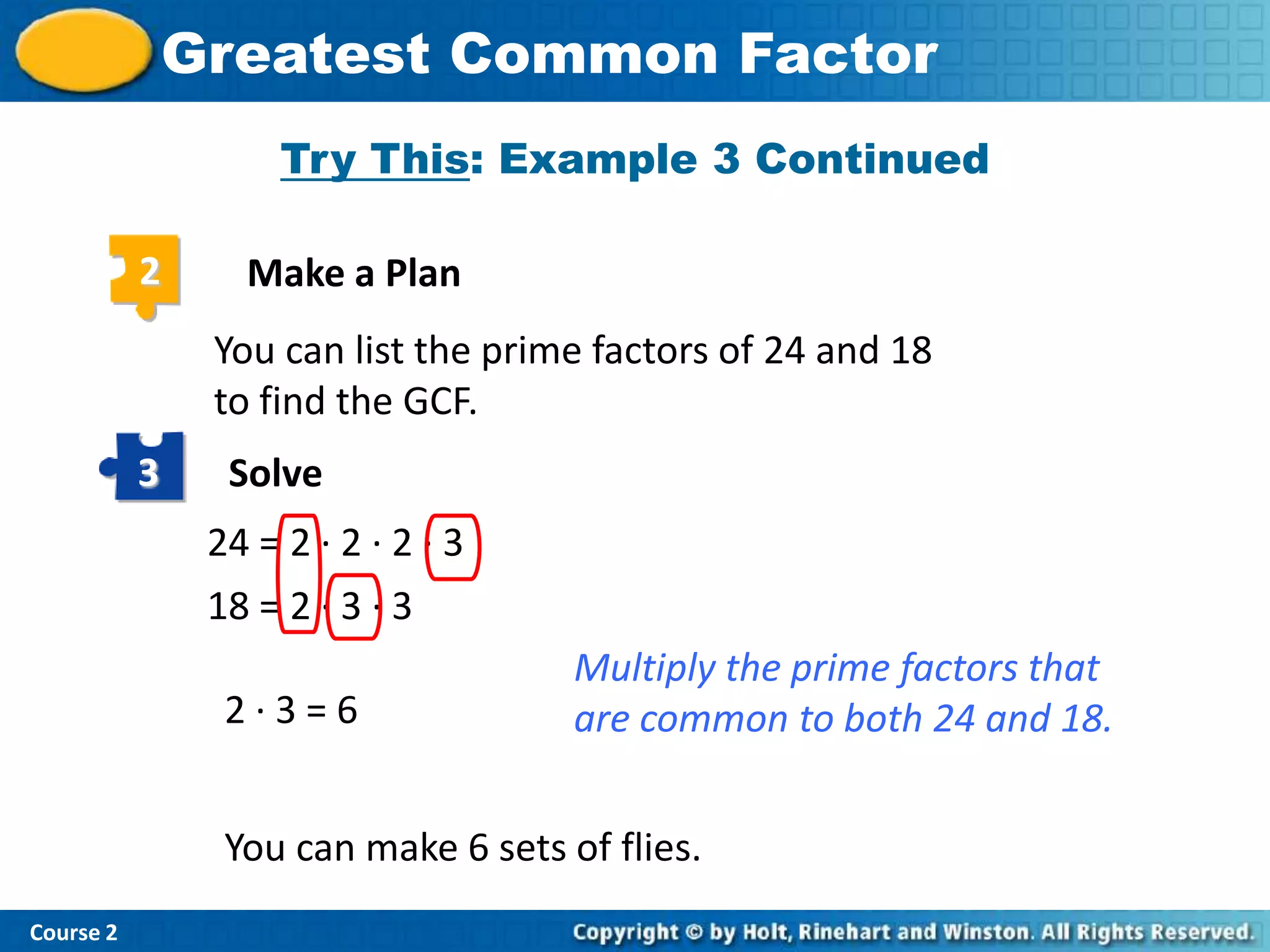
1) The document discusses number theory concepts such as divisibility, prime numbers, greatest common divisor, and relatively prime numbers. 2) It provides definitions, theorems, proofs, and examples to illustrate these concepts. For instance, it defines the greatest common divisor (GCD) as the largest integer that divides two numbers and proves properties of GCD. 3) The document presents three methods - using common divisors, prime factorizations, and the division algorithm - to calculate the GCD of two numbers.

1. Number Theory
by
Nittaya Noinan
Kanchanapisekwittayalai Phetchabun

2. Definitions.
Let a,b be integers with b ≠ 0. if there exists an
integer c such that a = bc,
we say b divides a which is denoted by b|a
b is called divisor of a
a is called multiple of b

3. Symbol .
b|a instead of “b divides a “
b|a instead of “b can’t divides a “

4. Example
1. 3 | 12 because 12 = 3 4
2. -5 | 15 because 15 = (-5) (-3)
3. 8 | 0 because 0 = 8 0
4. 9 | 30 because there is not integer c
to make 30 = 9c
5. 11 | 66 and 66 | 198 then 11 | 198
6. 21 | 126 and 126 | 882 then 21 | 882

5. Theorem 1.
Let a,b be integers with a ≠ 0 and b ≠ 0 .
if a | b and b there exists an integer x such
that b = ax c then a | c
Proof.
assume that a | b and b|c
there exists an integer x such that b = ax
there exists an integer y such that c = by
therefore c = (ax)y
c = a(xy) and xy be integer
thus a | c

6. Theorem 2.
If a,b be positive integers such a | b then a b
Proof.
assume that a | b
there exists an integer x such that b = ax
since a and b be positive integer then x be
positive integer
therefore x ≥ 1
then ax ≥ a ( because a be positive integer)
thus b ≥ a

7. Theorem 3.
If a,b and c be integers with a | b and a | c then
a | (bx + cy) when x and y be each integer.
Proof. bx + cy is called linear combination of b and c
assume that a | b and a | c
there exists an integer d such that b = ad
there exists an integer e such that c = ae
therefore bx + cy = (ad)x + (ae)y (when x and y be integer)
= a (dx + ey) (since dx + ey be integer)
thus a | (bx + cy)

8. Prime numbers
Definition. Let positive integer P is prime numbers
if and only if p 1 and if there exist integer x
divided p then x { 1 , -1 , p , -p}
Example. The following is a prime numbers
2, 3 , 5, 7, 11 , 13 , 17 , 19 , 23 etc.
A number that has only 1 and itself as factors is a
prime number.
A number like 24 that has factors other than 1 and
itself is called a composite number.

9. Example. Composite number
24 = 4 6
= 2 2 2 3
= 23 3 (composite numbers can write
be factor a prime number)
120 = 10 12
= 2 5 2 2 3
= 23 3 5 (composite numbers can
write be factor a prime number)

10. Theorem 4.
Fundamental Theorem of Arithmetic
The fundamental theorem of arithmetic states that any
integer n > 1 can be expressed uniquely as a product of
prime numbers apart from the order of primes.
6 3 2 or 36 2 2 3 3
Express 430 as a product of prime numbers.
430 2 215
215 5 43 430 2 5 43
43 43 1

11. Division Algorithm
Theorem 5. Division Algorithm. if a and b
be integers with b 0 then There exist
uniquely determined integers q and r such that
a = bq + r and 0 r < b
q is called quotient and
r is called remainder

12. Example.
1) 4 = 9(0) + 4
2) 24 = 4(6) + 0
3) 62 = 12(5) + 2
4) -22 = 6(-4) + 2
5) -34 = 5(7) + 1

13. Denifition.
integer a be even number if and only if
there exit integer k such that a = 2k
integer a be odd number if and only if
there exit integer k such that a = 2k + 1

14. Example. 1
Prove that “Squares of odd numbers is odd”
Proof. Give a is odd numbers then there exist
integer k with a = 2k + 1
a2 = (2K + 1)2
= 4K2 + 4K + 1
= 2(2K2 + 2K) + 1
When K be integer then 2(2K2 + 2K) be even numbers
Then 2(2K2 + 2K) + 1 be odd numbers
Hence a2 be odd numbers

15. Example. 2
Prove that “when 6 divides integer x then it has
remainder be 3. find the remainder when
6 divides 3x “
Proof. when 6 divides integer x then it has
remainder be 3 can write following
x = 6n + 3 when n be integer
3x = 18n + 9
3x = 18n + 6 + 3
3x = 6(3n + 1) + 3
Hence when 3x is divided by 6 has remainder is 3

16. Example.3
Give n be positive integers .Find the remainder
when n(n+1)(n+2) is divided by 3 .
Proof. When n is divided by 3 .it will probability
has remainder are 0 , 1 and 2 .
Case 1. when the remainder is 0 can be write n
following n = 3k when k is integer .
then n(n+1)(n+2) = 3k(3k+1)(3k+2)
Thus n(n+1)(n+2) divided by 3 has remainder is
0 because 3 3k

17. Case 2. when the remainder is 1 can be write n
following n = 3k + 1 when k is integer .
then n(n+1)(n+2) = (3k+1)(3k+2)(3k+3)
Thus n(n+1)(n+2) divided by 3 has remainder is
0 because 3 (3k + 3)
Case 3. when the remainder is 2 can be write n
following n = 3k + 2 when k is integer .
then n(n+1)(n+2) = (3k+2)(3k+3)(3k+4)
Thus n(n+1)(n+2) divided by 3 has remainder is
0 because 3 (3k + 3)
Hence from all 3 cases we can said n(n+1)(n+2)
divided by 3 has remainder is 0

18. Example.4
Find all positive integer that divide between
417 and 390 with the remainder equally.
Proof. Give x be positive integer that
divide between 417 and 390 with remainder is r
Then 417 = kx + r when k be integer ..(1)
390 = mx + r when m be integer..(2)
(1) – (2) then 27 = (k – m)x …(3)

19. Since k – m be integers thus x 27
Thus the possible value of x is 1, 3 , 9 , 27
Of checking see that 1 and 3 divide between 419
and 390 and the remainder is 0 equally ,
9 divide between 419 and 390 and the remainder
is 3 equally and 27 divide between 419 and 390
and the remainder is 12 equally .
Hence all positive integer that divide between
417 and 390 with the remainder equally are
1 , 3 , 9 and 27

20. Theorem 6.
Let b be integer more than 1 .each integer n
can write in distributed base b such that
n = akbk + ak-1bk-1 +…+ a1b + a0
When k is integer and a0 , a1 , a2 ,…,ak be
not negative integer and less than with b and
ak 0

21. Proof. By division algorithm.
When n is divided by b then the quotient q0
and remainder a0 such that
n = bq0 + a0 0 a0 b ….1)
q0 is divided by b such that
q0 = bq1 + a1 0 a1 b ….2)
To do it as same the upper until the quotient be zero
q1 = bq2 + a2 0 a2 b
q2 = bq3 + a3 0 a3 b
.
.
.

22. qk-2 = bqk-1 + ak-1 0 ak-1 b
qk-1 = b(0) + ak 0 ak b
Since n q0 q1 q2 …≥ 0 is not negative integer
Sequence that is decreased. Thus the division
algolithm have to finished by the last quotience
is zero.

23. From 1) n = bq0 + a0
Instead q0 by 2) then n = b(bq1 + a1 ) + a0
Then = b2q1 + a1b + a0
Do it as same the upper then
n = b3q2 + a2b2 + a1b + a0
.
.
.
n = bk-1qk-2 + ak-2bk-2 +..+ a1b + a0
n = bkqk-1 + ak-1bk-1 +..+ a1b + a0
Since 3) qk-1 = ak
Thus n = akbk + ak-1bk-1 +..+ a1b + a0

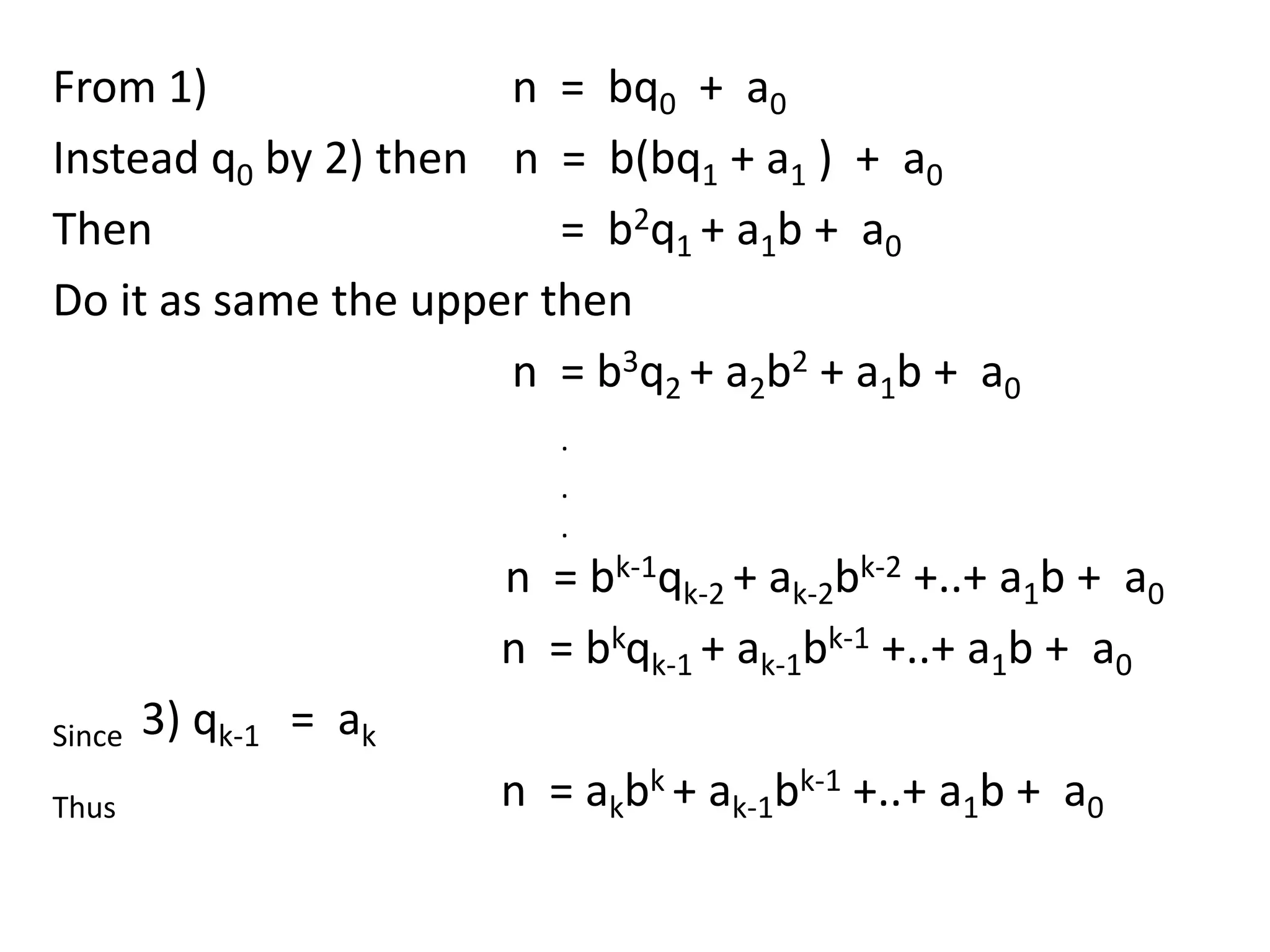
24. Example. Write 96 in distributed base 5.
Solve. 96 = (5 19) + 1
19 = (5 3) + 4
3 = ( 5 0) + 3
Then
96 = (5 19) + 1
= [5 (5 3) + 4 ] + 1
= (52 3)+( 5 4) + 1
Hence 96 = (3 52)+(4 5) + 1
We use symbol ( akak-1 …a0 )b instead of
akbk + ak-1bk-1 +..+ a1b + a0
Hence 96 = (3 52)+(4 5) + 1 = (341) 5

25. Example. Write 25 in distributed base 2.
Solve. 25 = (2 24) + 1
24 = (2 12) + 0
12 = ( 2 6) + 0
6 = ( 2 3) + 0
3 = ( 2 1) + 1
1 = ( 2 0) + 1
Hence 25 = (11001) 2

26. Example. Write 12345 in distributed base 8.
Solve. 12345 = (8 1543) + 1
1543 = (8 192) + 7
192 = ( 8 24) + 0
24 = ( 8 3) + 0
3 = ( 8 0) + 3
Hence 12345 = (30071) 8

27. Greatest Common Divisor
Relatively Prime
Definition. Let a,b be integers. Integer c which
divide of a and b is called common divisor
Definition. Let a,b be integers, not both zero.
The greatest common divisor of a and b
(or gcd(a,b) ) is the biggest number d which
divides both a and b.
Definition. a and b are said to be relatively prime
if gcd(a,b) = 1, so no prime common divisors.

28. The first ways to find the greatest common divisor.
1) The common divisor of 4 and 8 is 1, 2, 4
thus The greatest common divisor of 4 and 8 is 4
2) The common divisor of 8 and 12 is 1, 2, 4
thus The greatest common divisor of 4 and 8 is 4
3) The common divisor of 12 and 35 is 1
thus The greatest common divisor of 4 and 8 is 1
4) The common divisor of 24 and 32 is 1, 2, 4,
6, 8
thus The greatest common divisor of 4 and 8 is 8

29. The second ways to find the greatest common divisor.
1) Since 4 = 2 2
8 = 2 2 2
Thus The greatest common divisor of 4 and 8 is
2 2 = 4
2) Since 8 = 2 2 2
12 = 2 2 3
Thus The greatest common divisor of 8 and 12 is
2 2 = 4

30. The second ways to find the greatest common divisor.
3) Since 12 = 2 2 3
35 = 5 7
Thus there is no number is the same product of prime
numbers between 12 and 35 The greatest common
divisor of 12 and 35 is 1
4) Since 24 = 2 2 2 3
32 = 2 2 2 2 2
Thus The greatest common divisor of 4 and 8 is
2 2 2 = 8

31. The third ways to find the greatest common divisor.
1) Since 2 4 , 8
2 2 , 4
1 ,2
Thus The greatest common divisor of 4 and 8 is
2 2 = 4

32. The third ways to find the greatest common divisor.
2) Since 2 8 , 12
2 4 , 6
2 ,3
Thus The greatest common divisor of 4 and 8 is
2 2 = 4

33. The third ways to find the greatest common divisor.
3) Since 1 12 , 35
12 , 35
Thus there is no number divide 12 and 35
The greatest Common divisor of 12 and 35 is 1

34. The third ways to find the greatest common divisor.
4) Since 2 24 , 32
2 12 , 16
2 6 , 8
3 , 4
Thus The greatest common divisor of 24 and 32 is
2 2 2 = 8

35. The fourth ways to find the greatest common divisor.
Theorem 7. Euclidean Algorithm.
Euclidean Algorithm. Given integers a and b 1, use the
division algorithm repeatedly:
a = q1b + r1 0 r1 < a
b = q2r1 + r2 0 r2 < r1
r1 = q3r2 + r3 0 r3 < r2
...
...
r k-2= qkrk−1 + rk 0 rk < rk-1
rk−1 = qk+1rk
where in each equation the divisor at the preceding stage is
divided by the remainder. These remainders decrease
r1 > r2 > · · · 0

36. so the process eventually stops when the remainder
becomes zero. If r1 = 0, then gcd(a, b) = n. Otherwise,
rk = gcd(a, b), where rk is the last nonzero remainder
and can be expressed as a linear combination of a and
b by eliminating remainders.
Proof. Express rk as a linear combination of a and b by
eliminating remainders in the equations from the
second last equation up. Hence every common
divisor of a and b divides rk. But rk is itself a common
divisor of a and b (it divides every ri—work up through
the equations). Hence rk = gcd(a, b).

37. Two integers a and b are called relatively prime
if gcd(a, b) = 1.
Hence 12 and 35 are relatively prime, but this is not
true for 12 and 15
Because gcd(12, 15) = 3. Note that 1 is relatively
prime to every integer a. The following theorem
collects three basic properties of relatively prime
integers.

38. Example. 1. Find the gcd of 3240 and 2484
Solve.
3240 = 1(2484) + 756
2484 = 3(756) + 216
756 = 3(216) + 108
216 = 2(108) + 0
Hence (3240 , 2484) = 108

39. Example. 2. Find the gcd of 450 and 840
Solve.
840 = 1(450) + 390
450 = 1(390) + 60
390 = 6(60) + 30
60 = 2(30) + 0
Hence (450 , 840) = 30

40. Greatest Common Factor
Additional Example 1: Using a List to Find the GCF
Find the greatest common factor (GCF).
12, 36, 54
12: 1, 2, 3, 4, 6, 12 List all of the factors of
each number.
36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Circle the greatest
54: 1, 2, 3, 6, 9, 18, 27, 54 factor that is in all
the lists.
The GCF is 6.
Course 2

41. Insert Lesson TitleFactor
Greatest Common Here
Try This: Example 1
Find the greatest common factor (GCF).
14, 28, 63
14: 1, 2, 7, 14 List all of the factors of
each number.
28: 1, 2, 4, 7, 14, 28
Circle the greatest
63: 1, 3, 7, 9, 21, 63 factor that is in all
the lists.
The GCF is 7.
Course 2

42. Greatest Common Factor
Additional Example 2A: Using Prime Factorization to
Find the GCF
Find the greatest common factor (GCF).
A. 40, 56
40 = 2 · 2 · 2 · 5 Write the prime factorization of
each number and circle the
56 = 2 · 2 · 2 · 7 common factors.
2·2·2=8
Multiply the common prime factors.
The GFC is 8.
Course 2

43. Greatest Common Factor
Additional Example 2B: Using Prime Factorization to
Find the GCF
Find the greatest common factor (GCF).
B. 252, 180, 96, 60
Write the prime factorization
252 = 2 · 2 · 3 · 3 · 7 of each number and circle
180 = 2 · 2 · 3 · 3 · 5 the common prime factors.
96 = 2 · 2 · 2 · 2 · 2 · 3
60 = 2 · 2 · 3 · 5
2 · 2 · 3 = 12 Multiply the common prime
The GCF is 12. factors.
Course 2

44. Insert Lesson TitleFactor
Greatest Common Here
Try This: Example 2A
Find the greatest common factor (GCF).
A. 72, 84
72 = 2 · 2 · 2 · 9 Write the prime factorization of
each number and circle the common
84 = 2 · 2 · 7 · 3
factors.
2·2=4 Multiply the common prime factors.
The GCF is 4.
Course 2

45. Insert Lesson TitleFactor
Greatest Common Here
Try This: Example 2B
Find the greatest common factor (GCF).
B. 360, 250, 170, 40
360 = 2 · 2 · 2 · 9 · 5 Write the prime factorization
of each number and circle
250 = 2 · 5 · 5 · 5
the common prime factors.
170 = 2 · 5 · 17
40 = 2 · 2 · 2 · 5
2 · 5 = 10 Multiply the common prime
factors.
The GCF is 10.
Course 2

46. Greastest Common divisor Method # 3
Find the GCM of 48 and 80.
Common 2 48 80
Factors 2 24 40
Once 2 12 20
2 6 10
3 5
Remaining
2 · 2 · 2 · 2 = 16 Factors
2
The GCF is 16.

47. Greastest Common divisor Method # 3
Find the LCM of 108 , 45 and 90.
Common 3 108 45 90
Factors 2 36 15 30
Once 3 18 15 15
5 6 5 5
6 1 1
Remaining
3 · 2 · 3 · 5 = 90 Factors
The GCF is 90.

48. Greatest Common Factor
Additional Example 3: Problem Solving Application
You have 120 red beads, 100 white beads, and 45 blue
beads. You want to use all the beads to make bracelets
that have red, white, and blue beads on each. What is
the greatest number of matching bracelets you can
make?
Course 2

49. Greatest Common Factor
Additional Example 3 Continued
1 Understand the Problem
Rewrite the question as a statement.
• Find the greatest number of matching bracelets you can
make.
List the important information:
• There are 120 red beads, 100 white beads,
and 45 blue beads.
• Each bracelet must have the same
number of red, white, and blue beads.
The answer will be the GCF of 120, 100, and 45.
Course 2

50. Greatest Common Factor
Additional Example 3 Continued
2 Make a Plan
You can list the prime factors of 120, 100,
and 45 to find the GFC.
3 Solve
120 = 2 · 2 · 2 · 3 · 5
100 = 2 · 2 · 5 · 5
45 = 3 · 3 · 5
The GFC of 120, 100, and 45 is 5.
You can make 5 bracelets.
Course 2

51. Greatest Common Factor
Additional Example 3 Continued
4 Look Back
If you make 5 bracelets, each one will have
24 red beads, 20 white beads, and 9 blue
beads, with nothing left over.
Course 2

52. Insert Lesson TitleFactor
Greatest Common Here
Try This: Example 3
Nathan has made fishing flies that he plans to give
away as gift sets. He has 24 wet flies and 18 dry flies.
Using all of the flies, how many sets can he make?
Course 2

53. Insert Lesson TitleFactor
Greatest Common Here
Try This: Example 3 Continued
1 Understand the Problem
Rewrite the question as a statement.
• Find the greatest number of sets of flies
he can make.
List the important information:
• There are 24 wet flies and 18 dry flies.
• He must use all of the flies.
The answer will be the GCF of 24 and 18.
Course 2

54. Greatest Common Factor
Try This: Example 3 Continued
2 Make a Plan
You can list the prime factors of 24 and 18
to find the GCF.
3 Solve
24 = 2 · 2 · 2 · 3
18 = 2 · 3 · 3
Multiply the prime factors that
2·3=6 are common to both 24 and 18.
You can make 6 sets of flies.
Course 2

55. Insert Lesson TitleFactor
Greatest Common Here
Try This: Example 3 Continued
4 Look Back
If you make 6 sets, each set will have
3 dry flies and 4 wet flies.
Course 2

56. Greatest Common Factor
Insert Lesson Title Here
Lesson Quiz: Part 1
Find the greatest common factor (GCF).
1. 28, 40 4
2. 24, 56 8
3. 54, 99 9
4. 20, 35, 70 5
Course 2

57. Greatest Common Factor
Insert Lesson Title Here
Lesson Quiz: Part 2
5. The math clubs from 3 schools agreed to a competition.
Members from each club must be divided into teams, and
teams from all clubs must be equally sized. What is the
greatest number of members that can be on a team if
Georgia has 16 members, William has 24 members, and
Fulton has 72 members?
8
Course 2

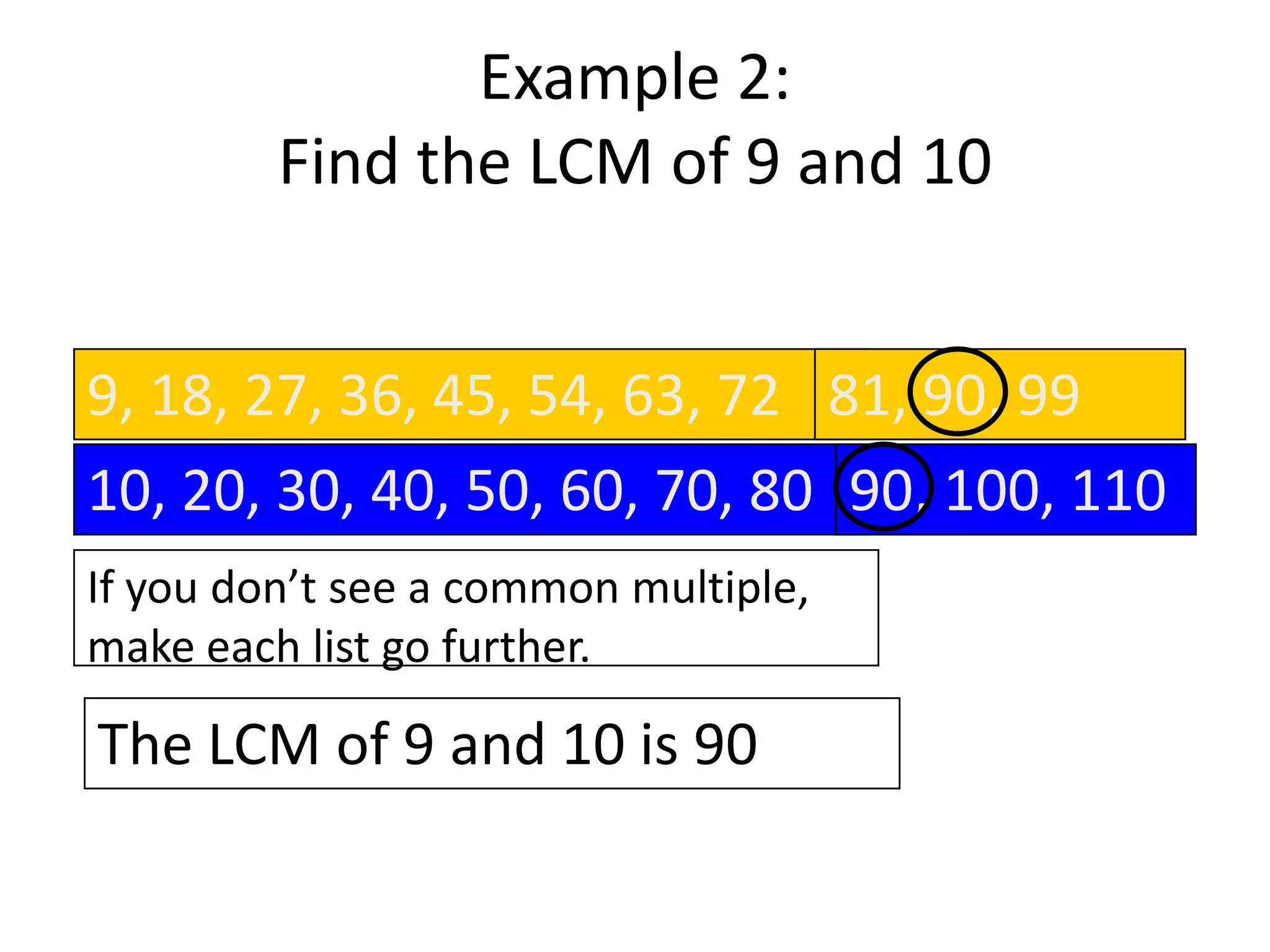
58. The Least Common Multiple
Definition. Let a,b be integers, not both zero.
The least common multiple of a and b
(or lcm[a,b]) is the least number c which
both a and b divides c.
Definition. Let a1 , a2 , a3 ,…,an be integers,not
both zero. Integer C is the least number which
a1 C , a2 C , …, an C is called The least
common multiple of a1 , a2 , a3 ,…,an
symbol is [a1 , a2 , a3 ,…,an ]

59. EXAMPLE:
Find the LCM of 12 and 18
The multiples of 12: The multiples of 18:
•12 x 1 = 12 •18 x 1 = 18
•12 x 2 =24 •18 x 2 = 36
•12 x 3 = 36 •18 x 3 = 54
•12 x 4 = 48 •18 x 4 = 72
•12 x 5 =60 •18 x 5 = 90

60. 12, 24, 36, 48, 60
18, 36, 54, 72, 90
The first number you see in both lists
is 36.
The least common multiple of 12
and 18 is 36.

61. Example 2:
Find the LCM of 9 and 10
9, 18, 27, 36, 45, 54, 63, 72 81, 90, 99
10, 20, 30, 40, 50, 60, 70, 80 90, 100, 110
If you don’t see a common multiple,
make each list go further.
The LCM of 9 and 10 is 90

62. Example 3:
Find the LCM of 4 and 12
4, 8, 12, 16
12, 24, 36
Answer: 12

63. Leastest Common Factor
Find the least common factor (LCF).
A. 40, 56
40 = 2 · 2 · 2 · 5 Write the prime factorization of
each number and circle the
56 = 2 · 2 · 2 · 7 common factors.
2 · 2 · 2 · 5 · 7 = 280
Multiply the common prime factors
The LCF is 280. and remainder number.
Course 2

64. Leastest Common Factor
Find the leatest common factor (LCF).
B. 252, 180, 96, 60
Write the prime factorization
252 = 2 · 2 · 3 · 3 · 7 of each number and circle
180 = 2 · 2 · 3 · 3 · 5 the common prime factors.
96 = 2 · 2 · 2 · 2 · 2 · 3
Multiply the common prime
60 = 2 · 2 · 3 · 5 factors and remainder number.
2 · 2 · 3 · 3 · 5 · 2 · 2 · 2 · 7 = 10080
The LCF is 10080.
Course 2

65. Insert Lesson TitleFactor
Leastest Common Here
Find the leastest common factor (LCF).
A. 72, 84
72 = 2 · 2 · 2 · 9 Write the prime factorization of
each number and circle the common
84 = 2 · 2 · 7 · 3
factors.
2 · 2 · 2 · 3 · 7 · 9 = 1512 Multiply the common prime factors
and remainder number.
The LCF is 1512.
Course 2

66. Least Common Multiple Method # 3
Find the LCM of 48 and 80.
Common 2 48 80
Factors 2 24 40
Once 2 12 20
2 6 10
3 5
Remaining
Factors
LCM 2 2 2 2 3 5
LCM 240

67. Least Common Multiple Method # 3
Find the LCM of 108 , 45 and 90.
Common 3 108 45 90
Factors 2 36 15 30
Once 3 18 15 15
5 6 5 5
6 1 1
Remaining
3 · 2 · 3 · 5 · 6 = 540 Factors
The LCF is 540.