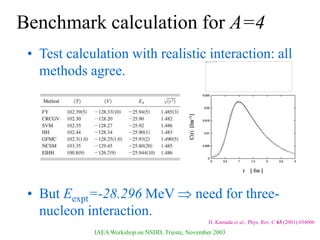
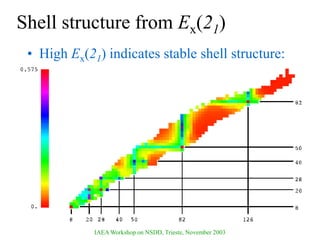
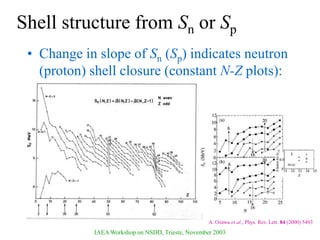
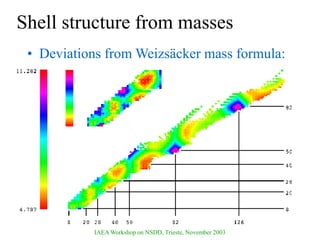
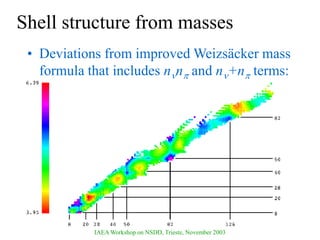
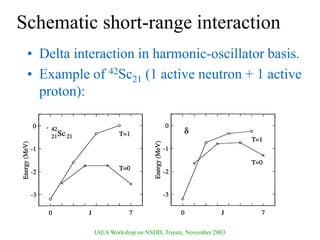
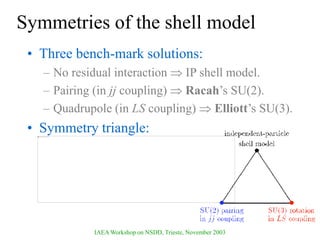
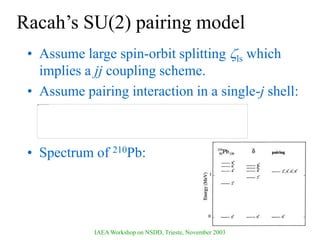
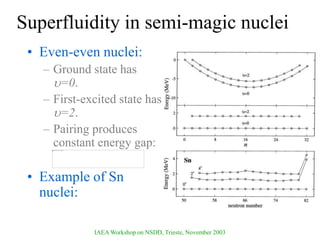
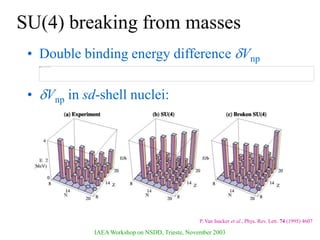
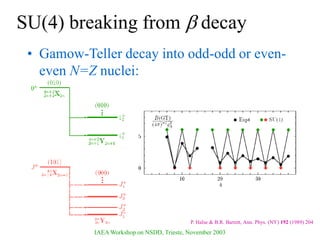
The document discusses various nuclear models, notably the nuclear shell model, and their underlying assumptions and symmetries, including Racah's SU(2) pairing model, Wigner's SU(4) symmetry, and Elliott's SU(3) model of rotation. It outlines different ab initio methods for nuclear calculations, benchmark tests, and the significance of symmetries in understanding nuclear structure and interactions, while providing insights into phenomena like superfluidity. Additionally, it addresses the effects of pairing interactions on nuclear behavior, the evidence for shell structures, and the breaking of these symmetries due to various interactions.