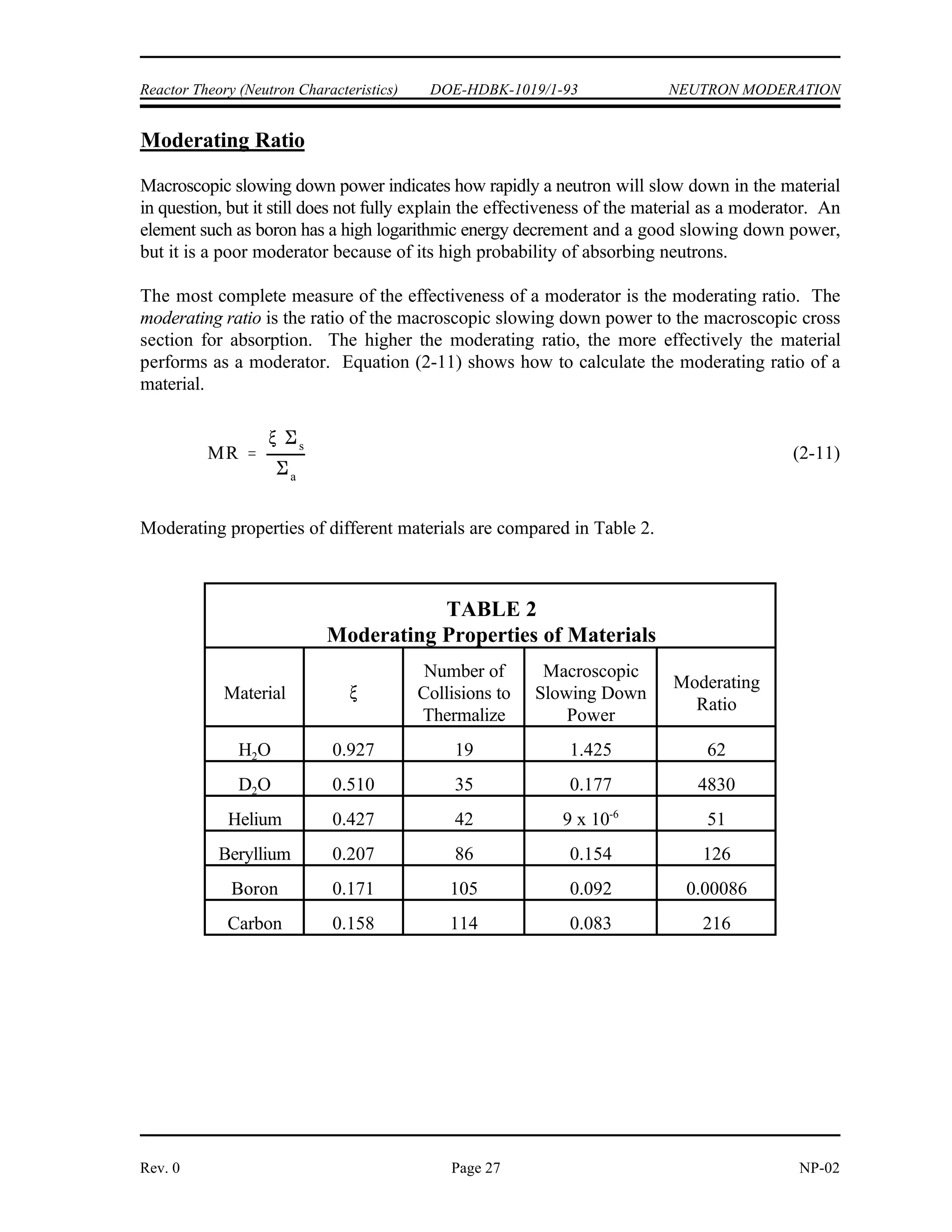
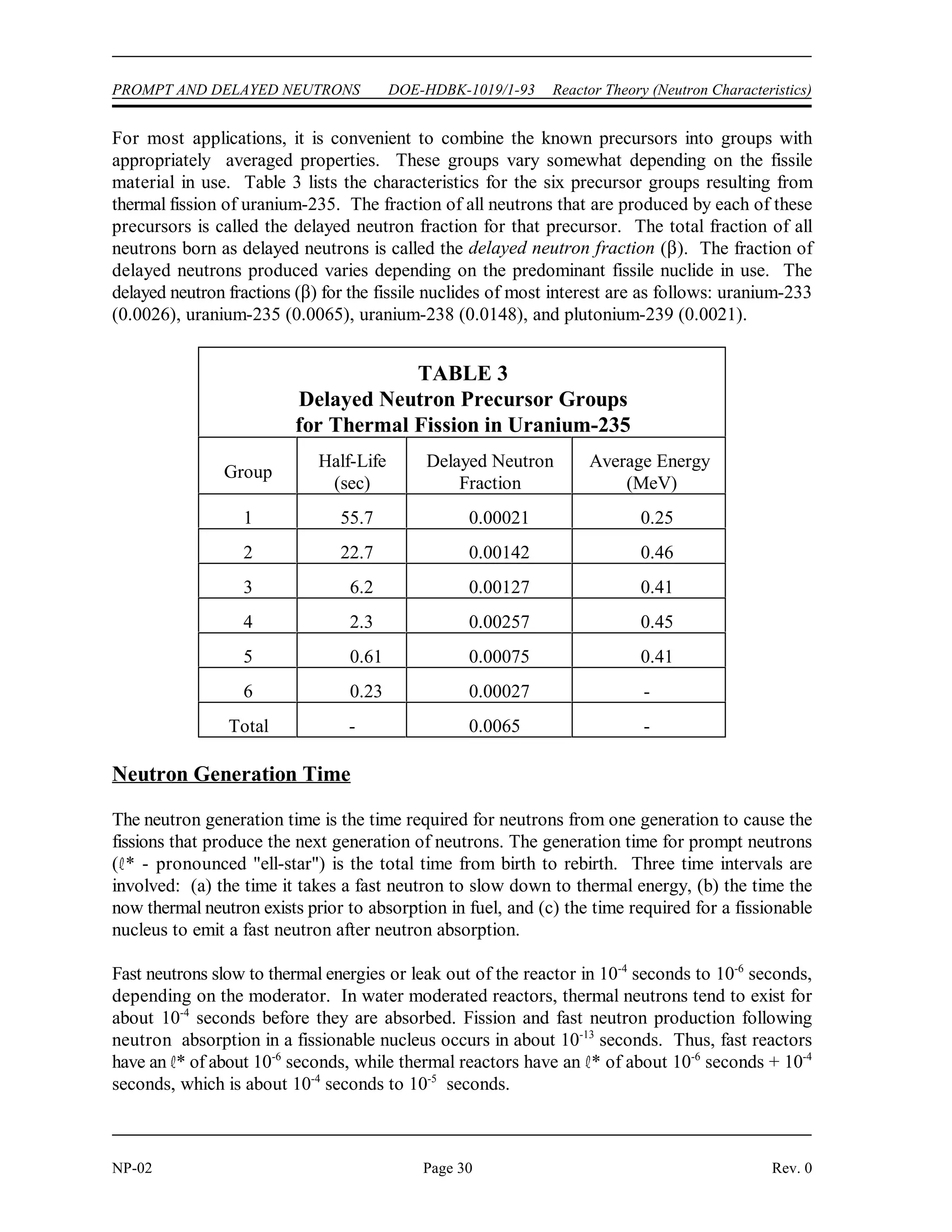
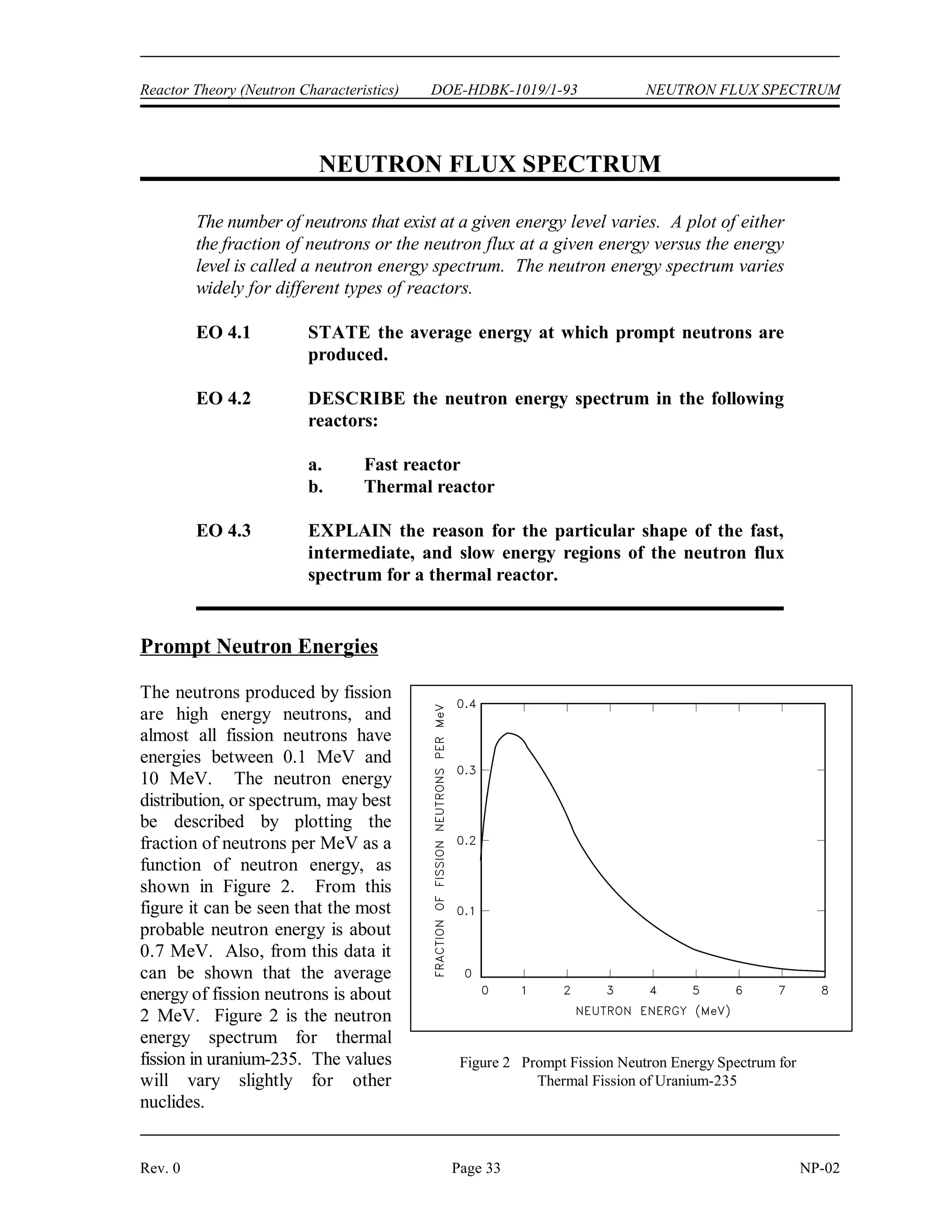
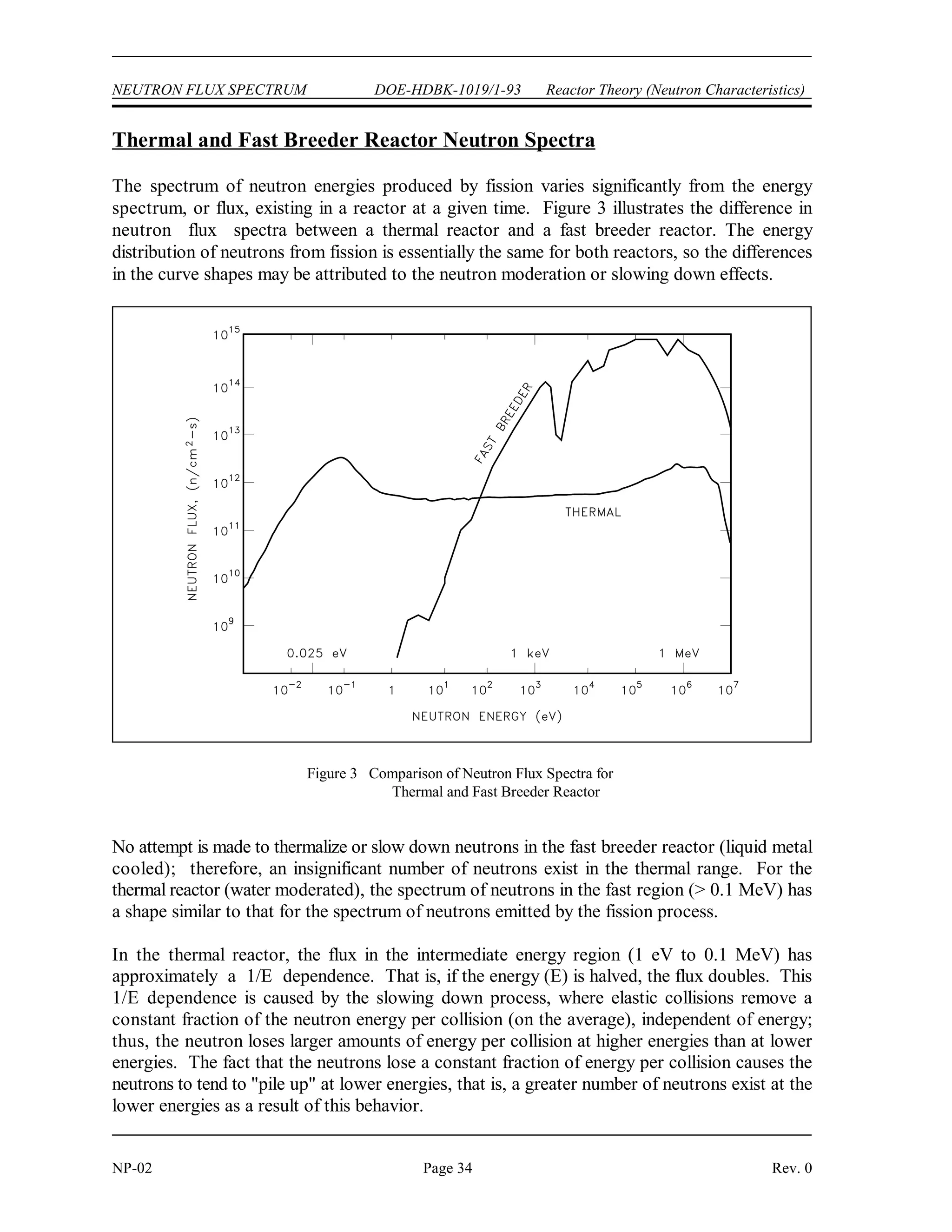
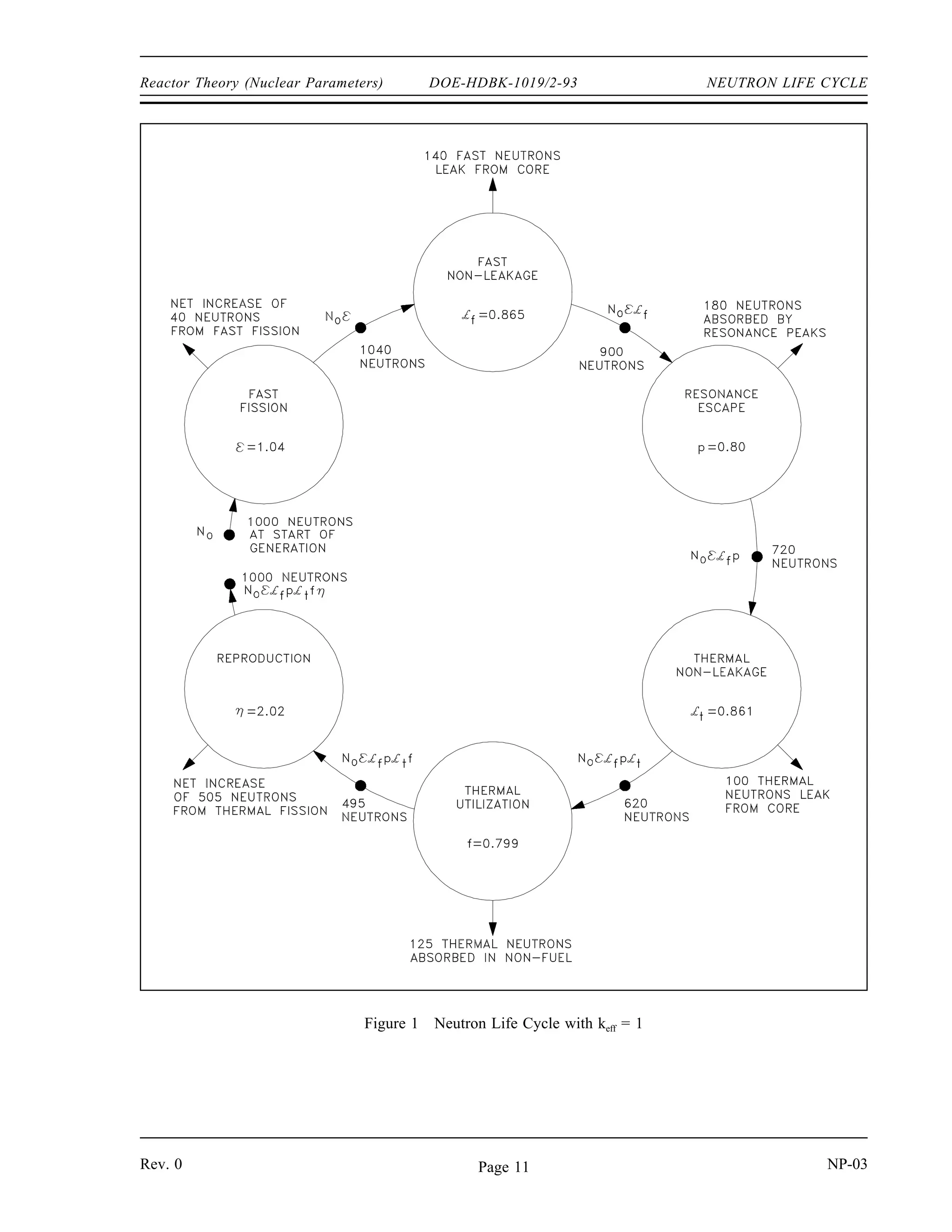
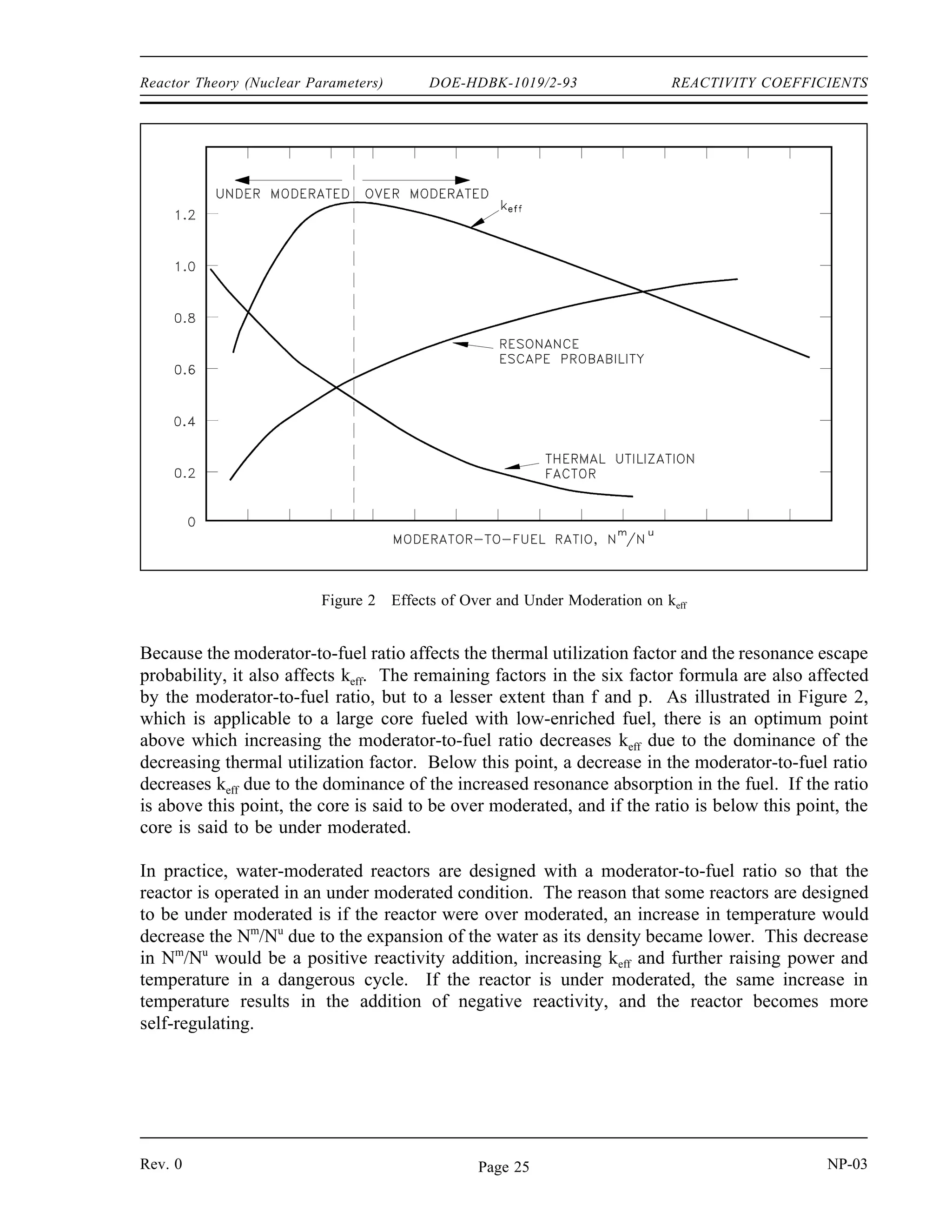
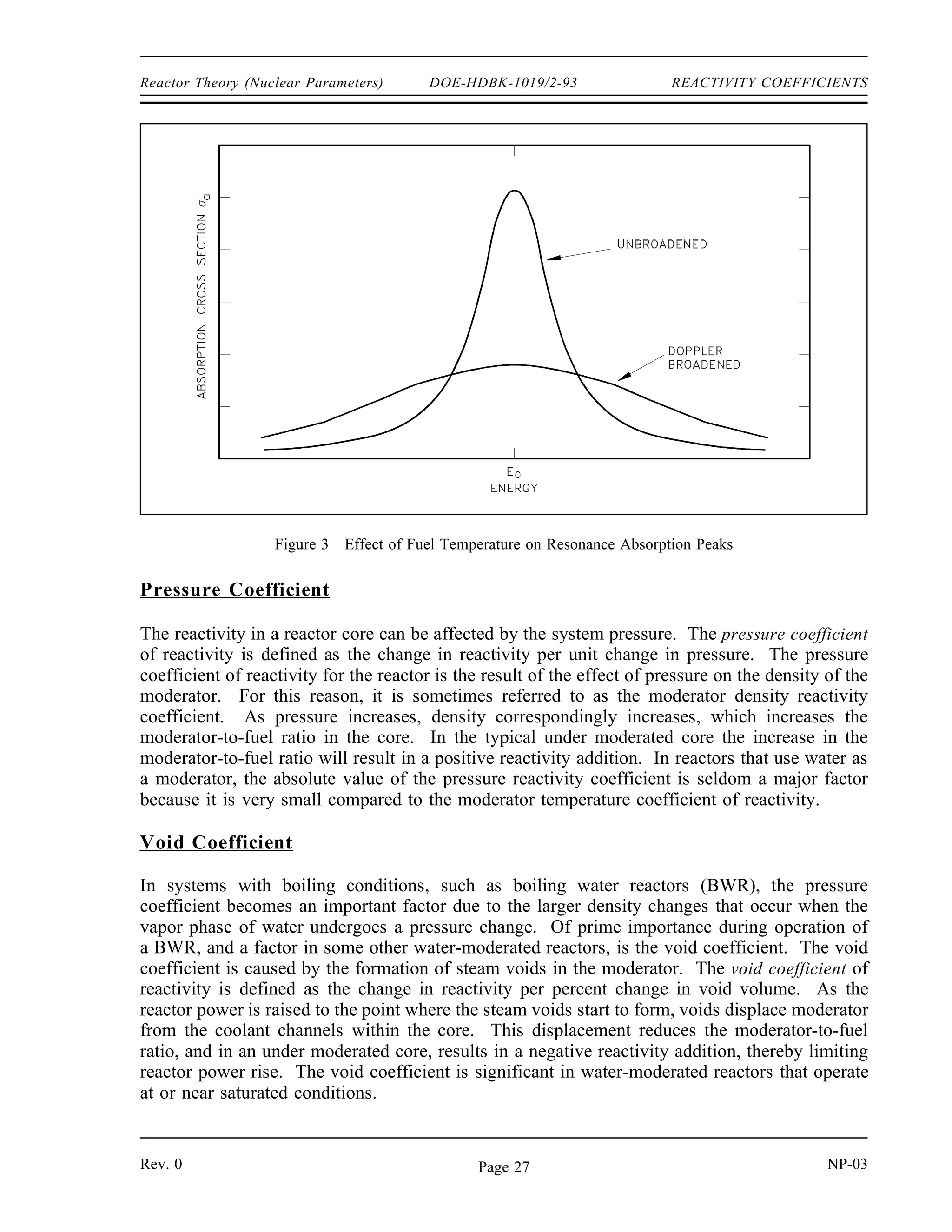
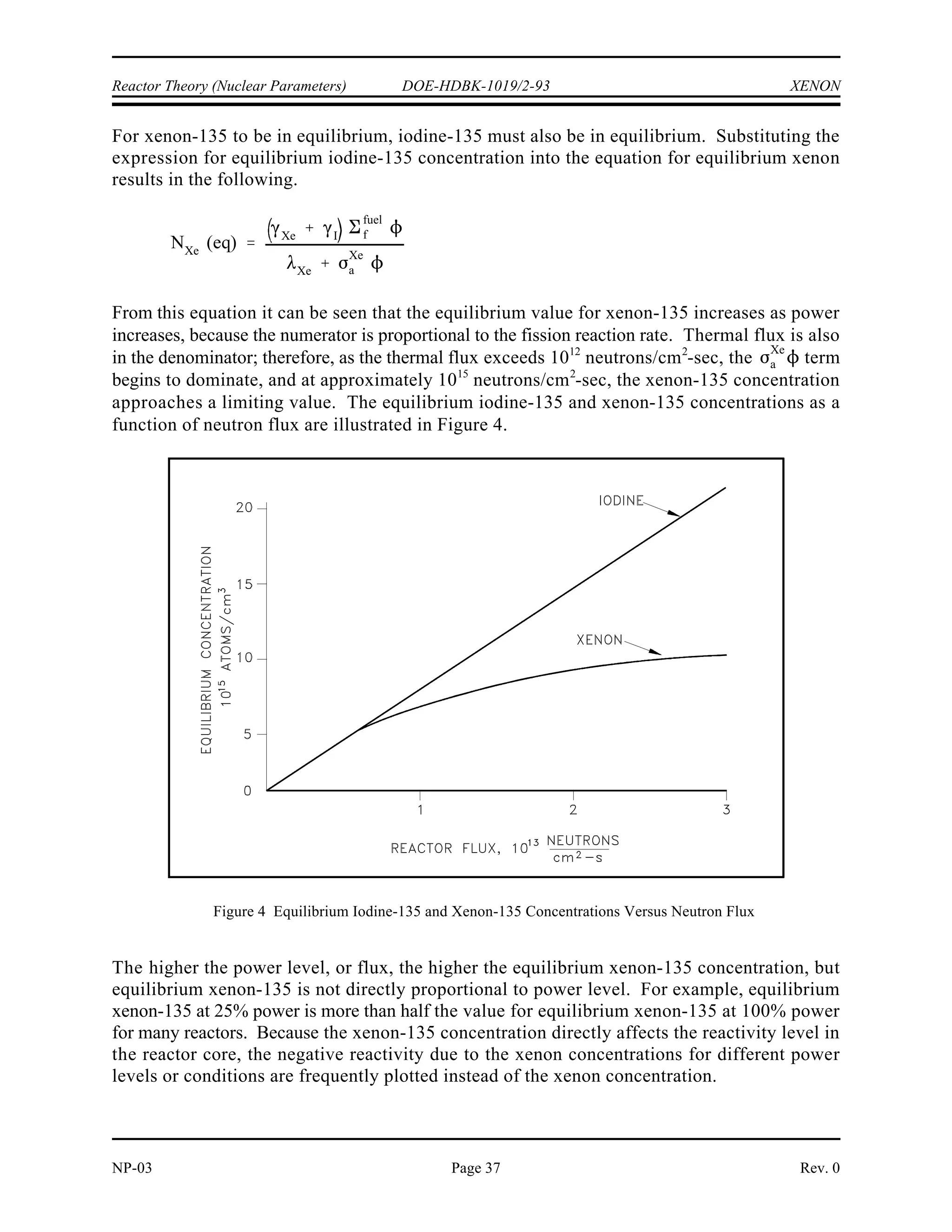
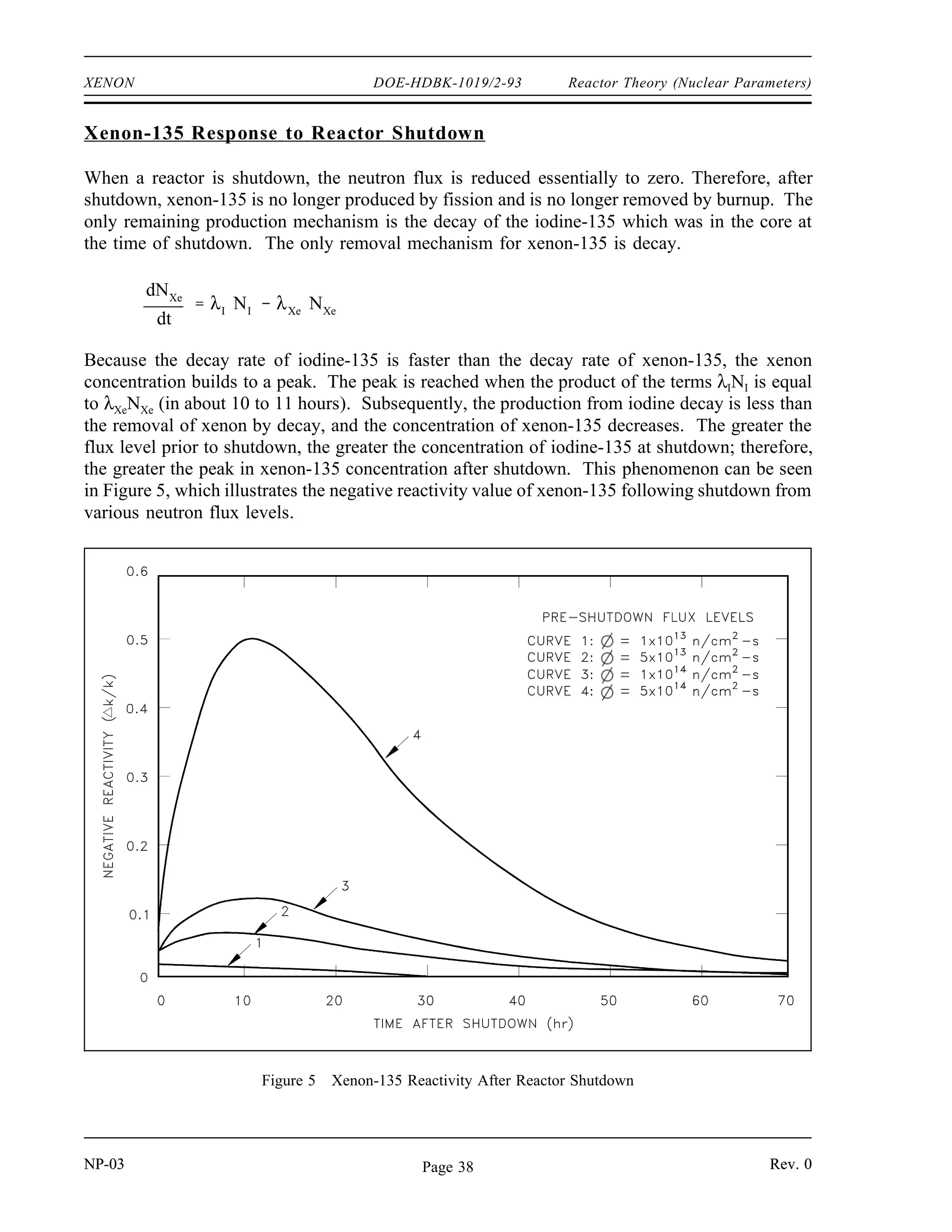
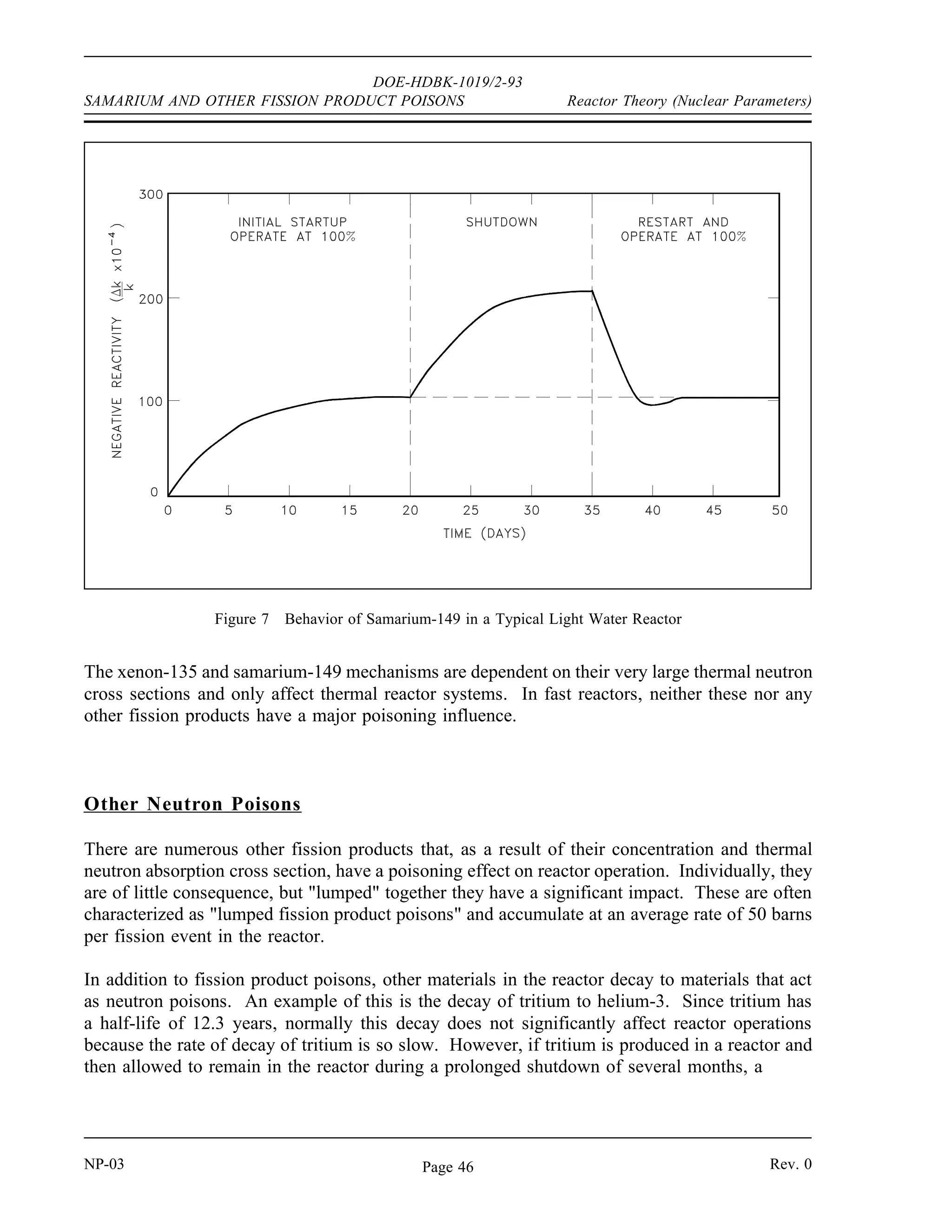
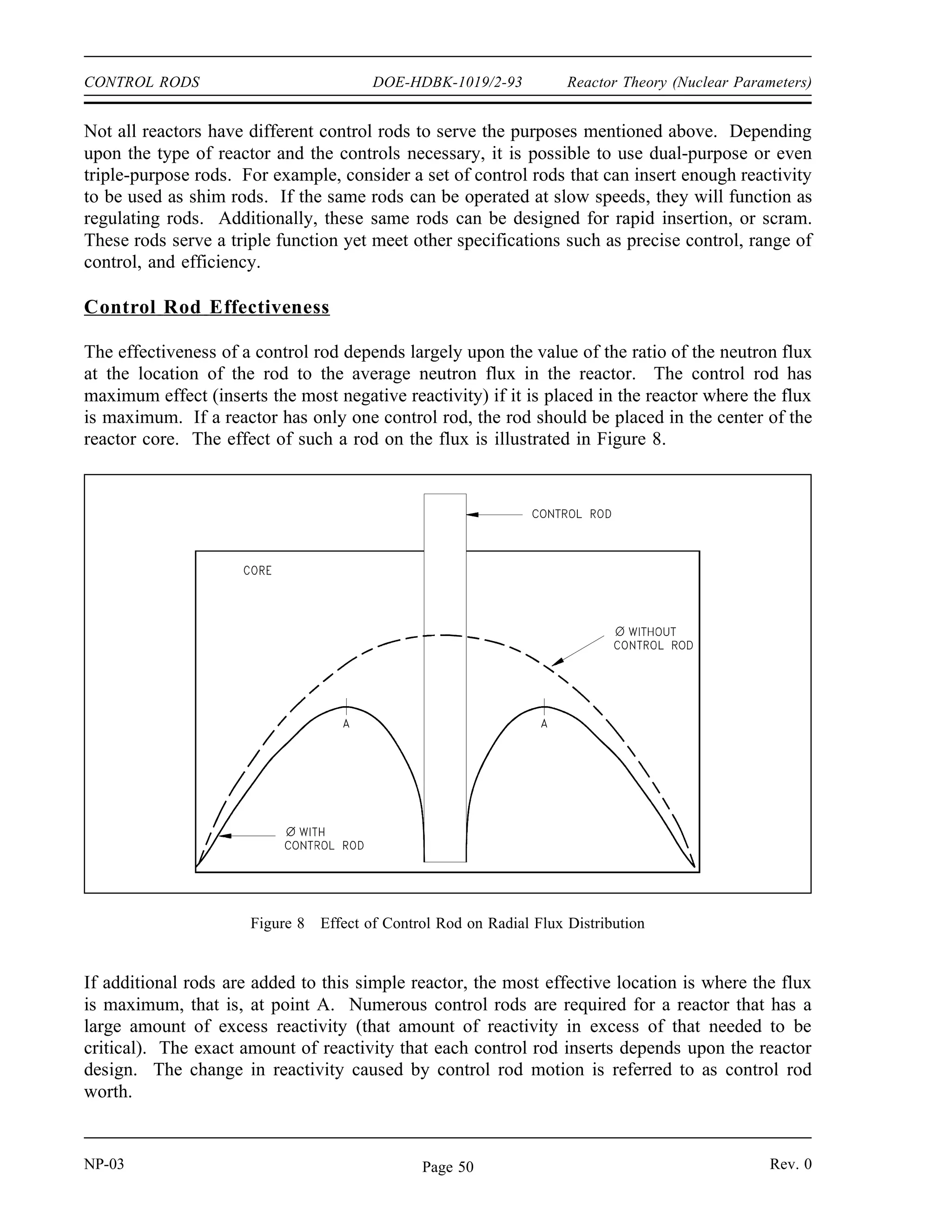
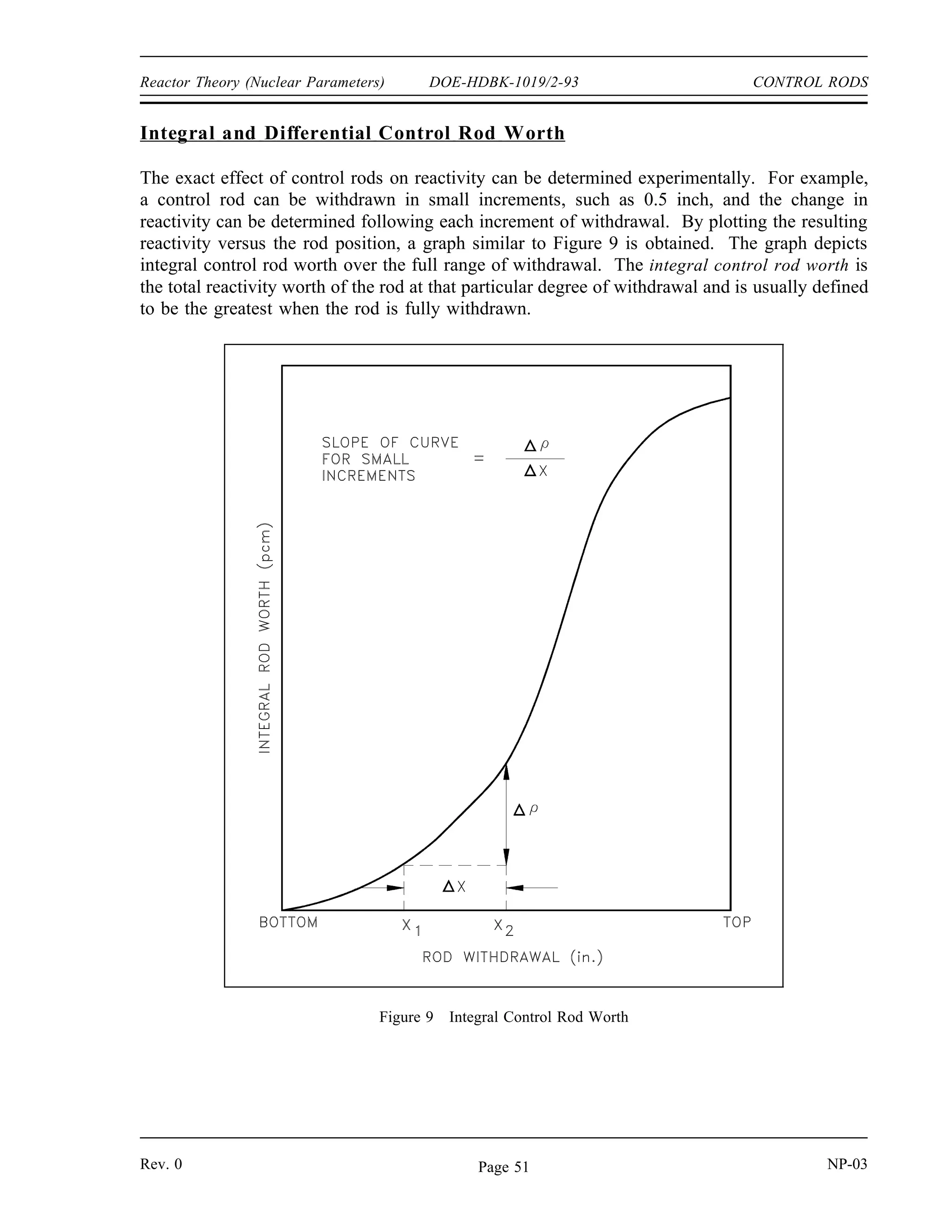
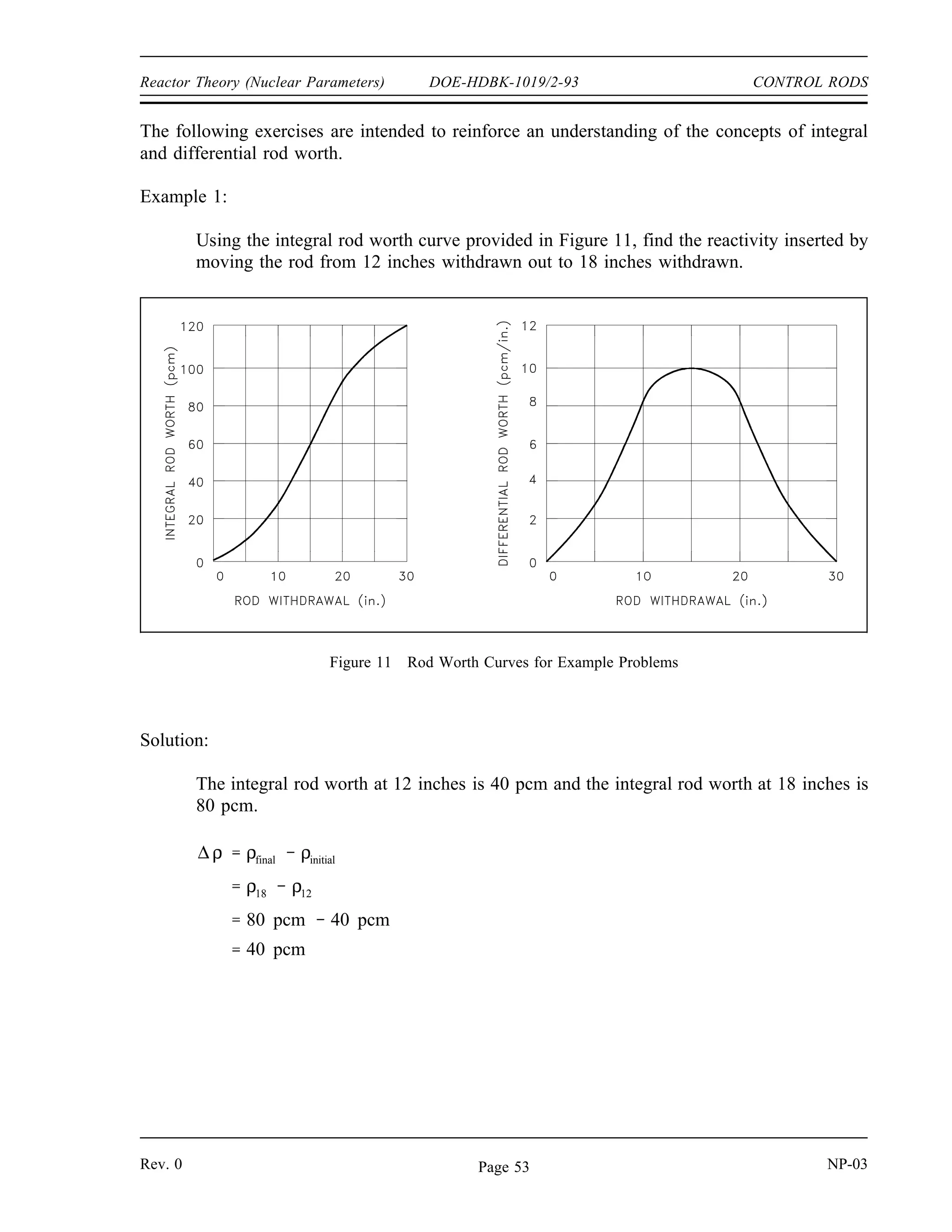
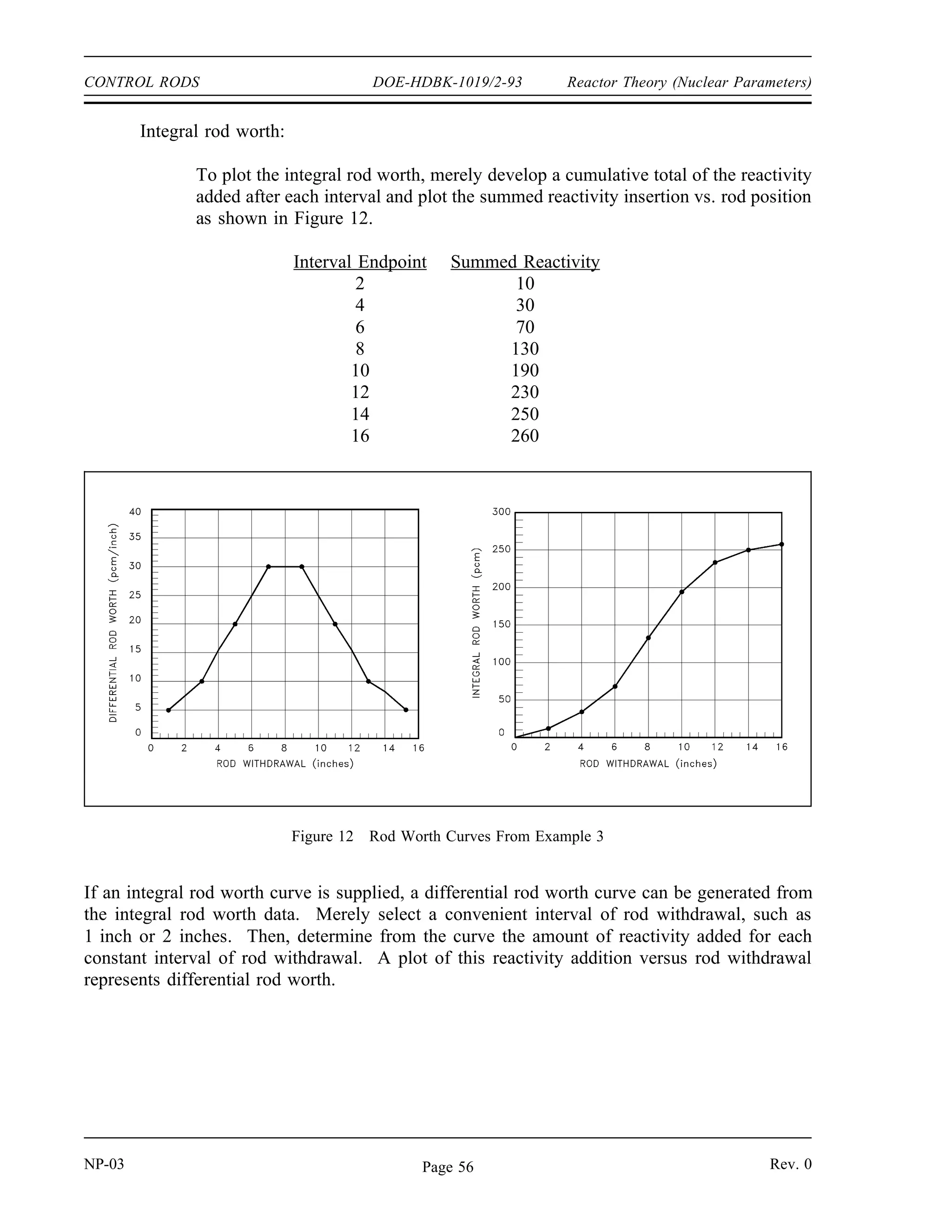
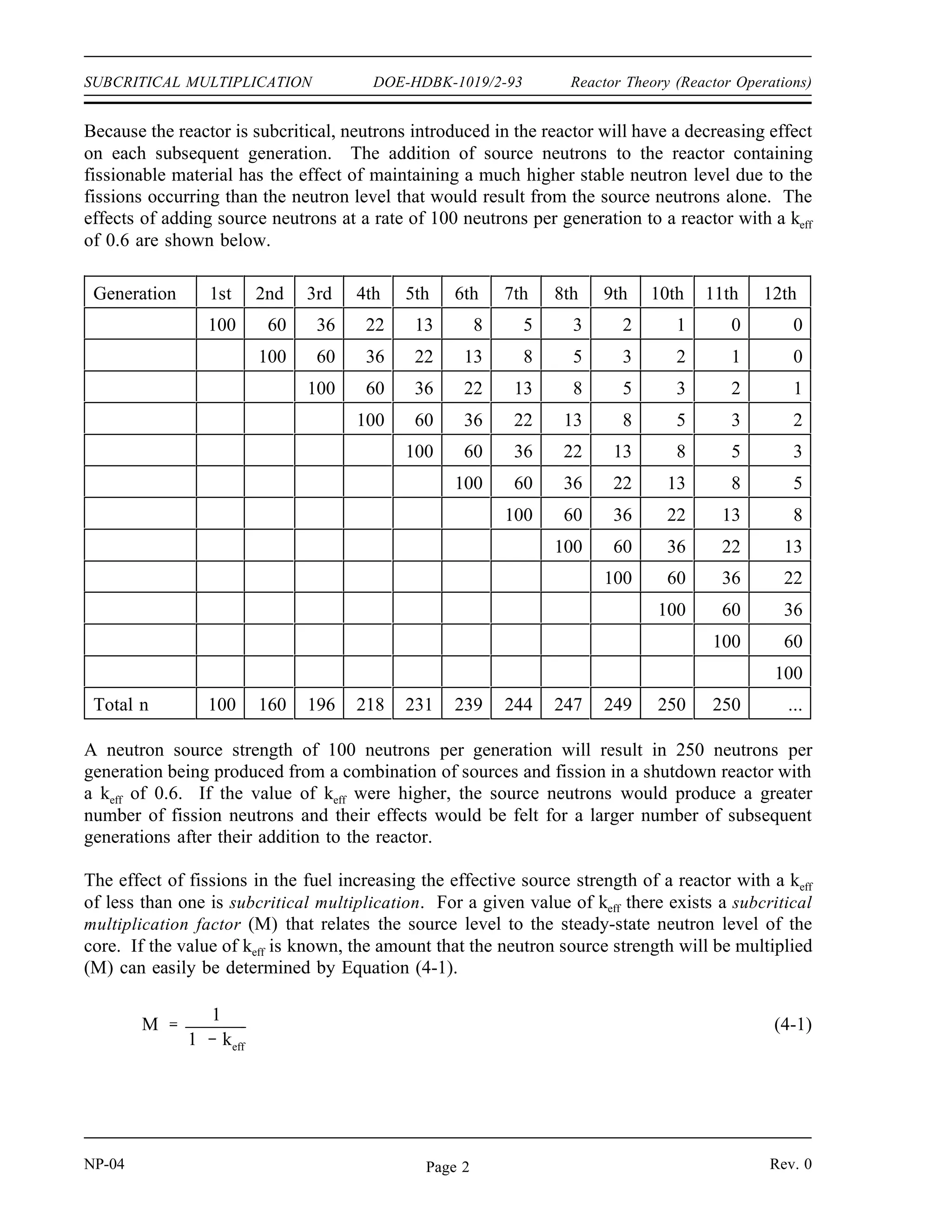
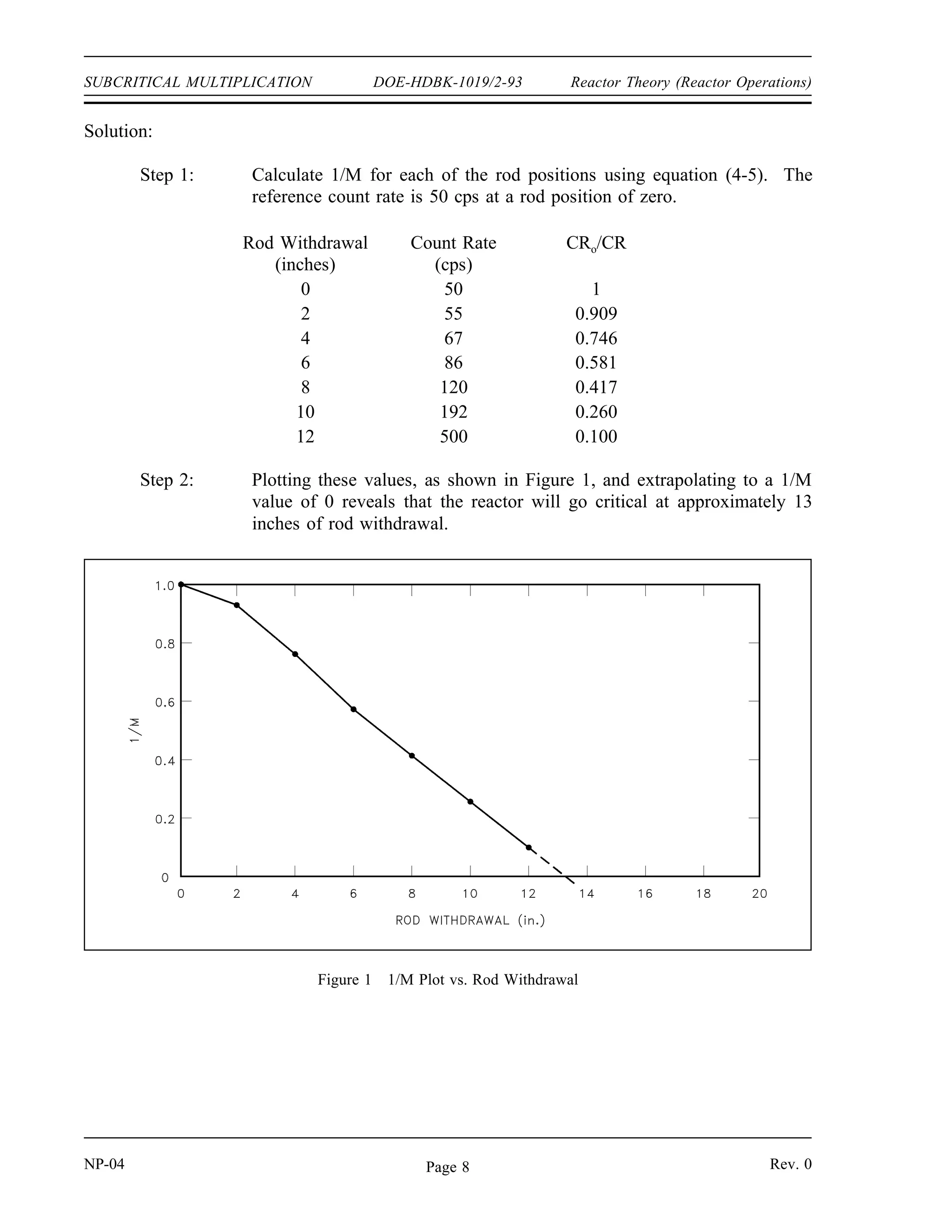
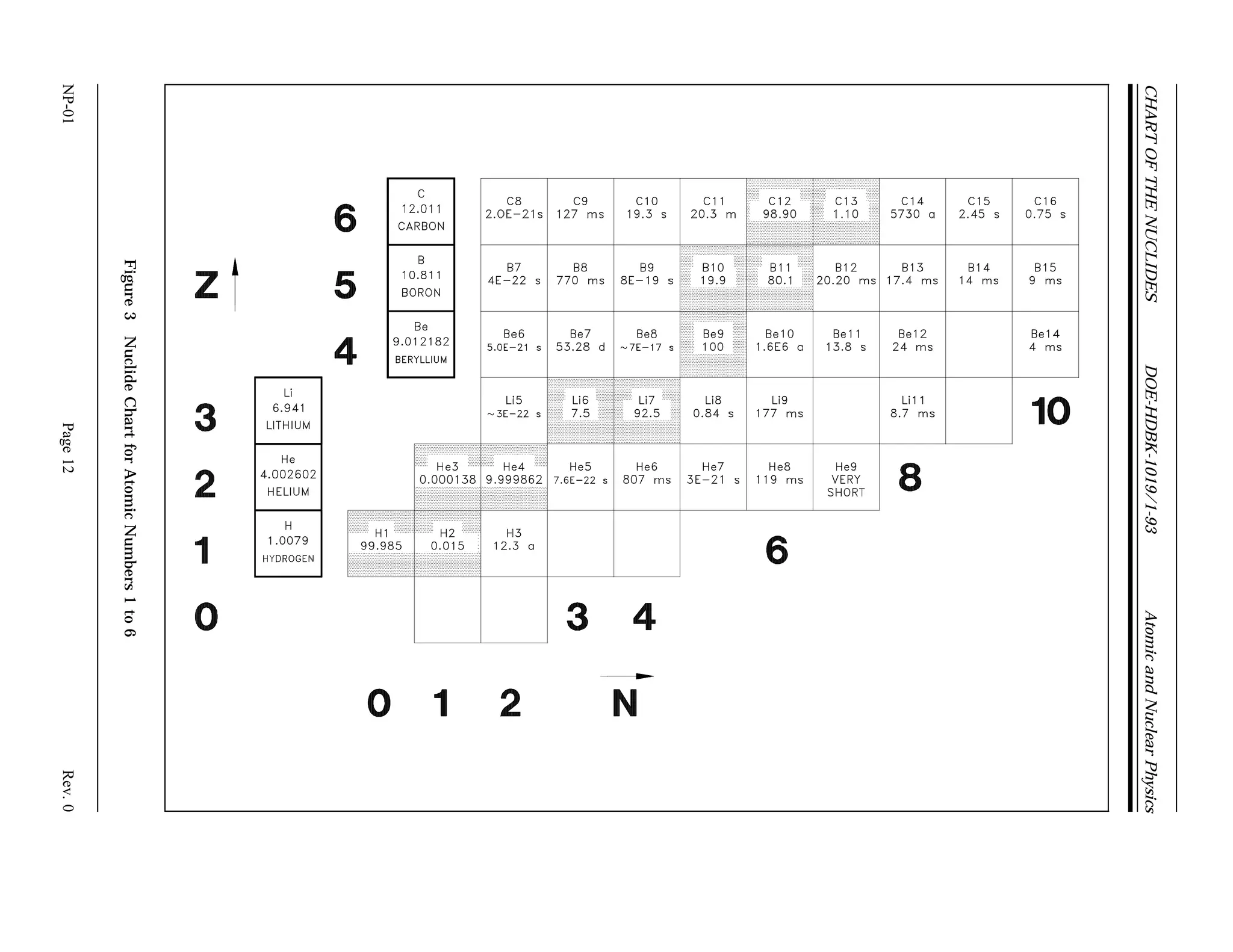
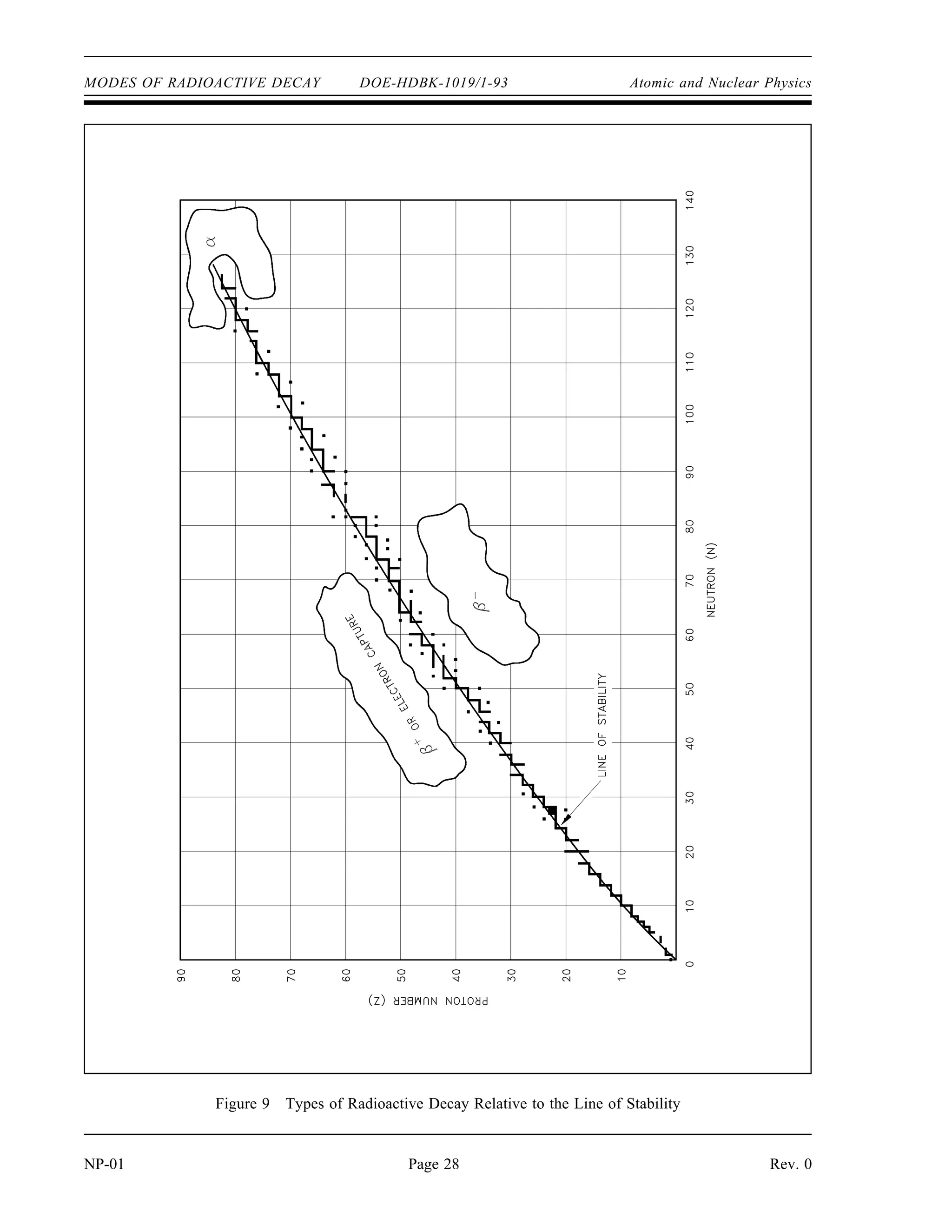
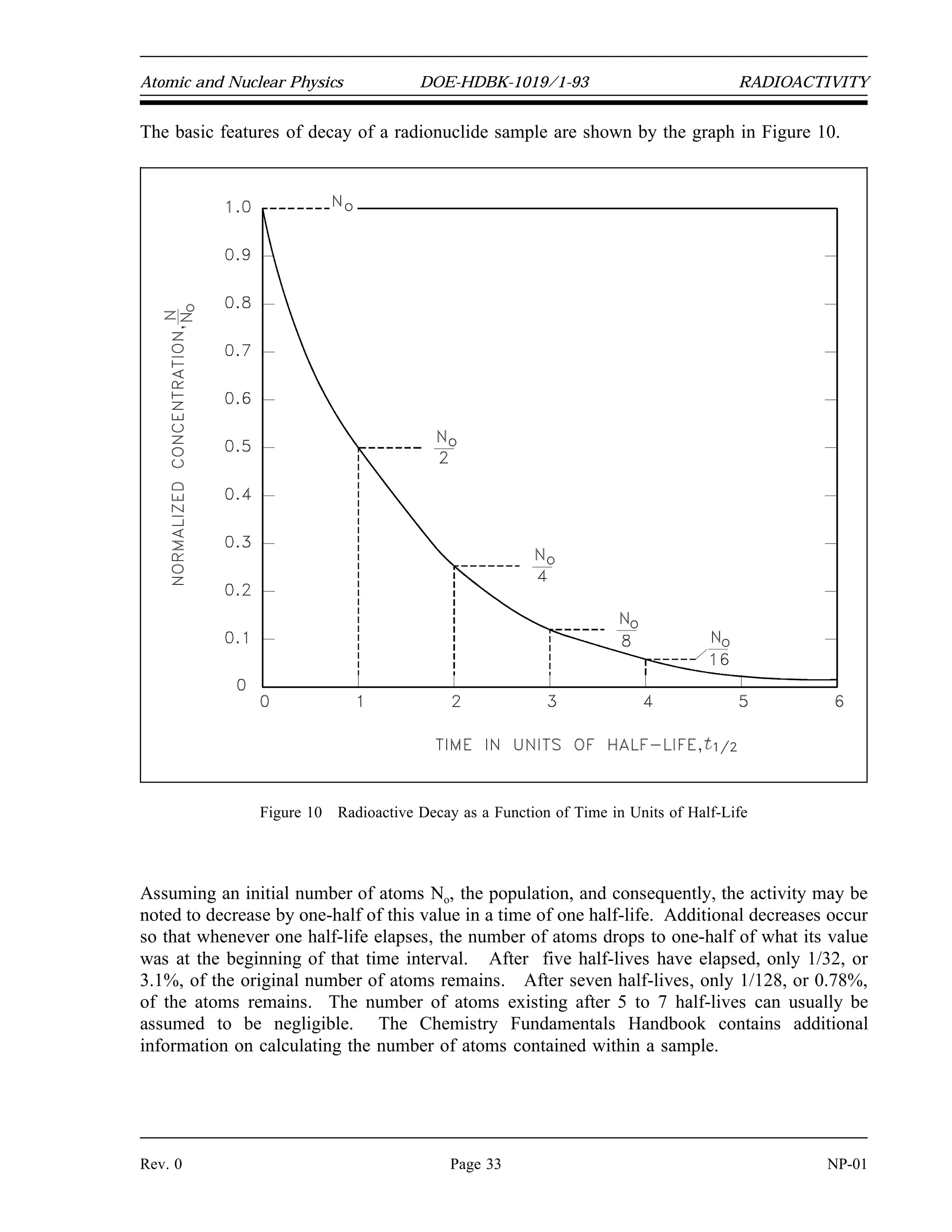
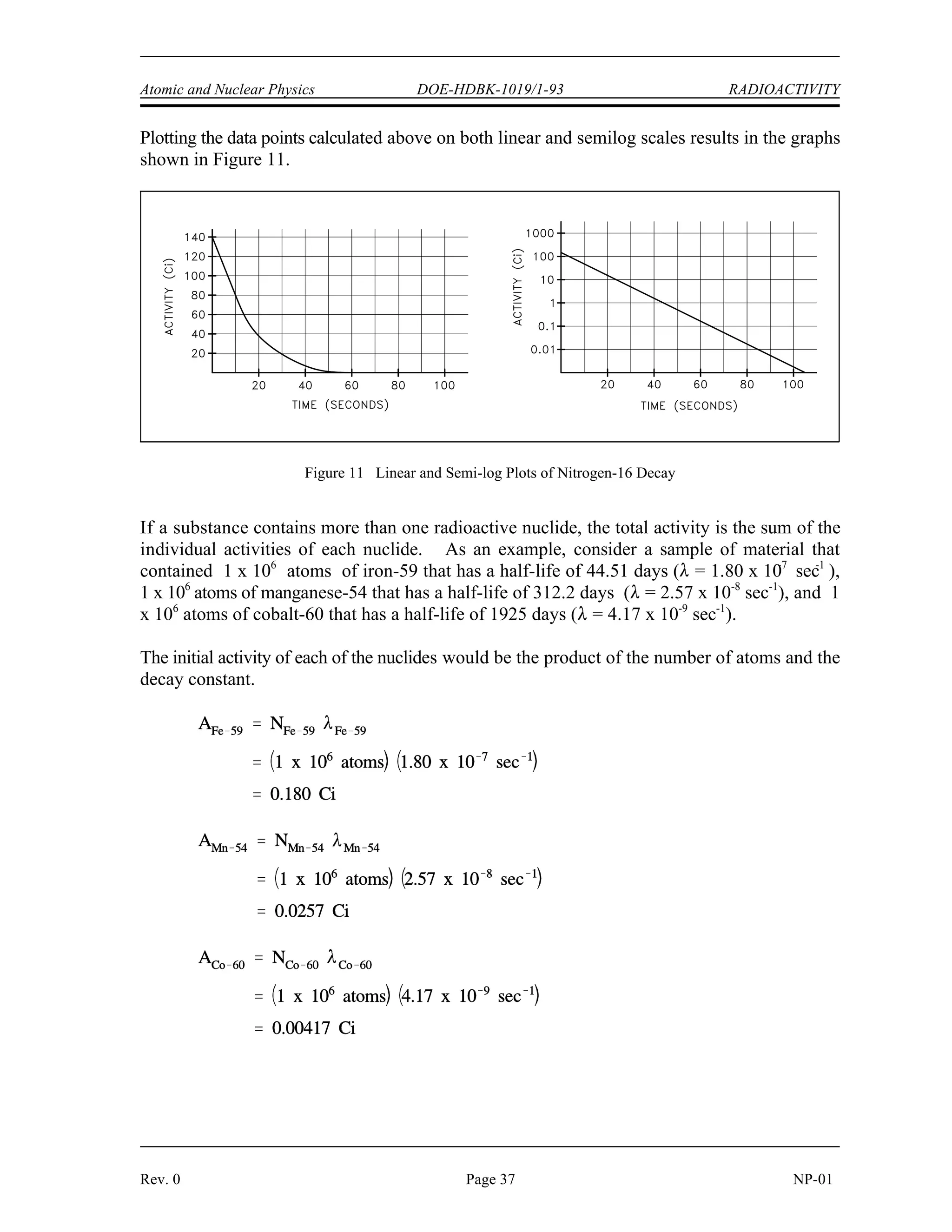
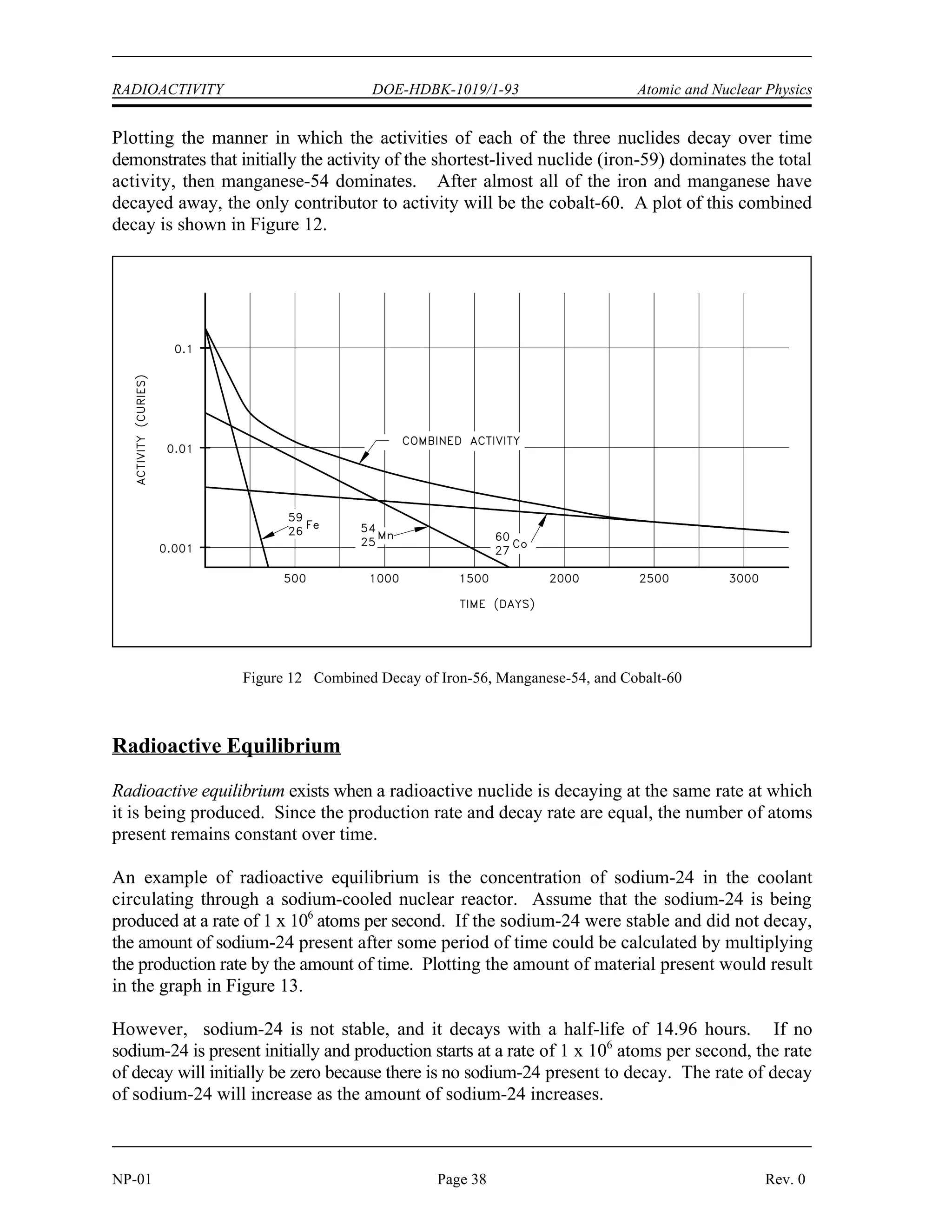
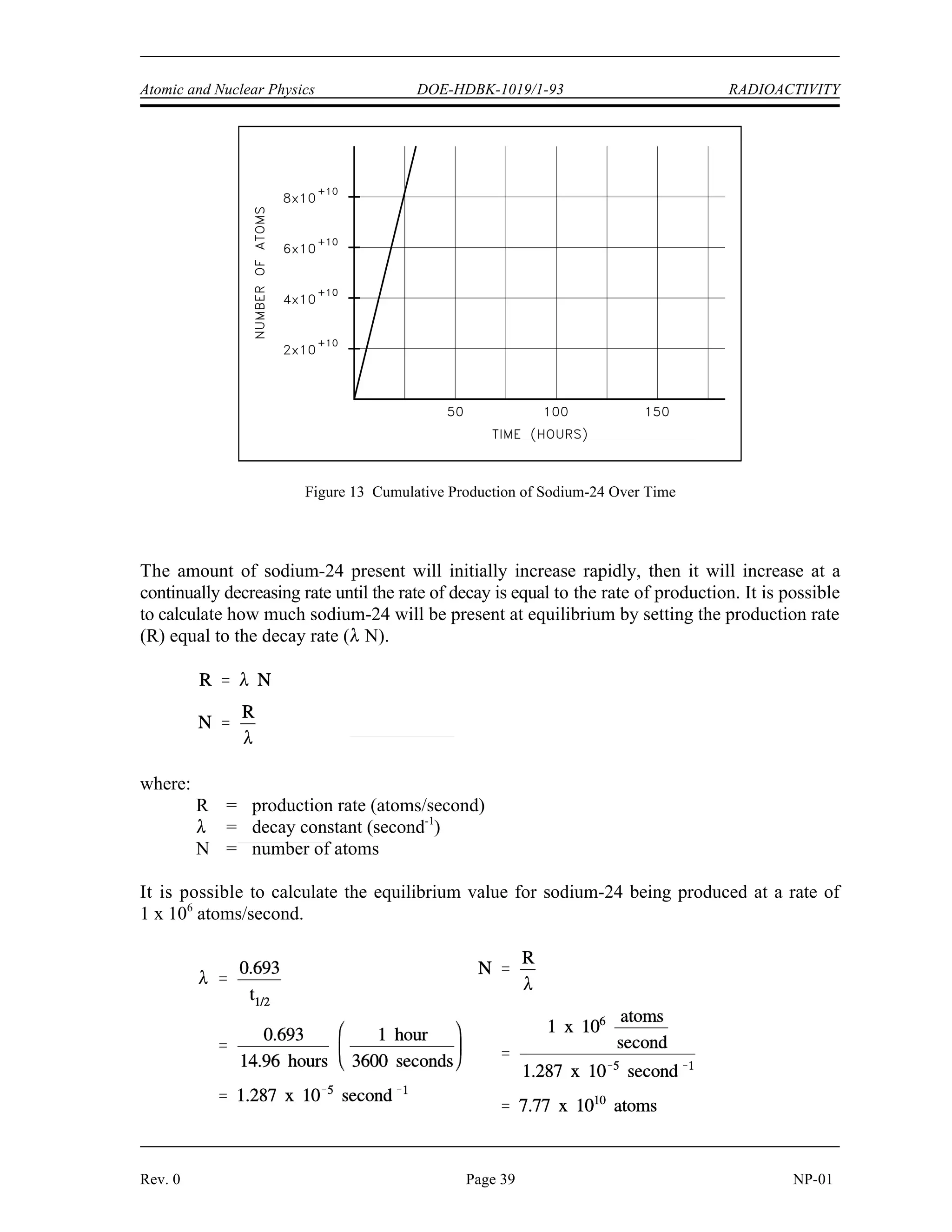
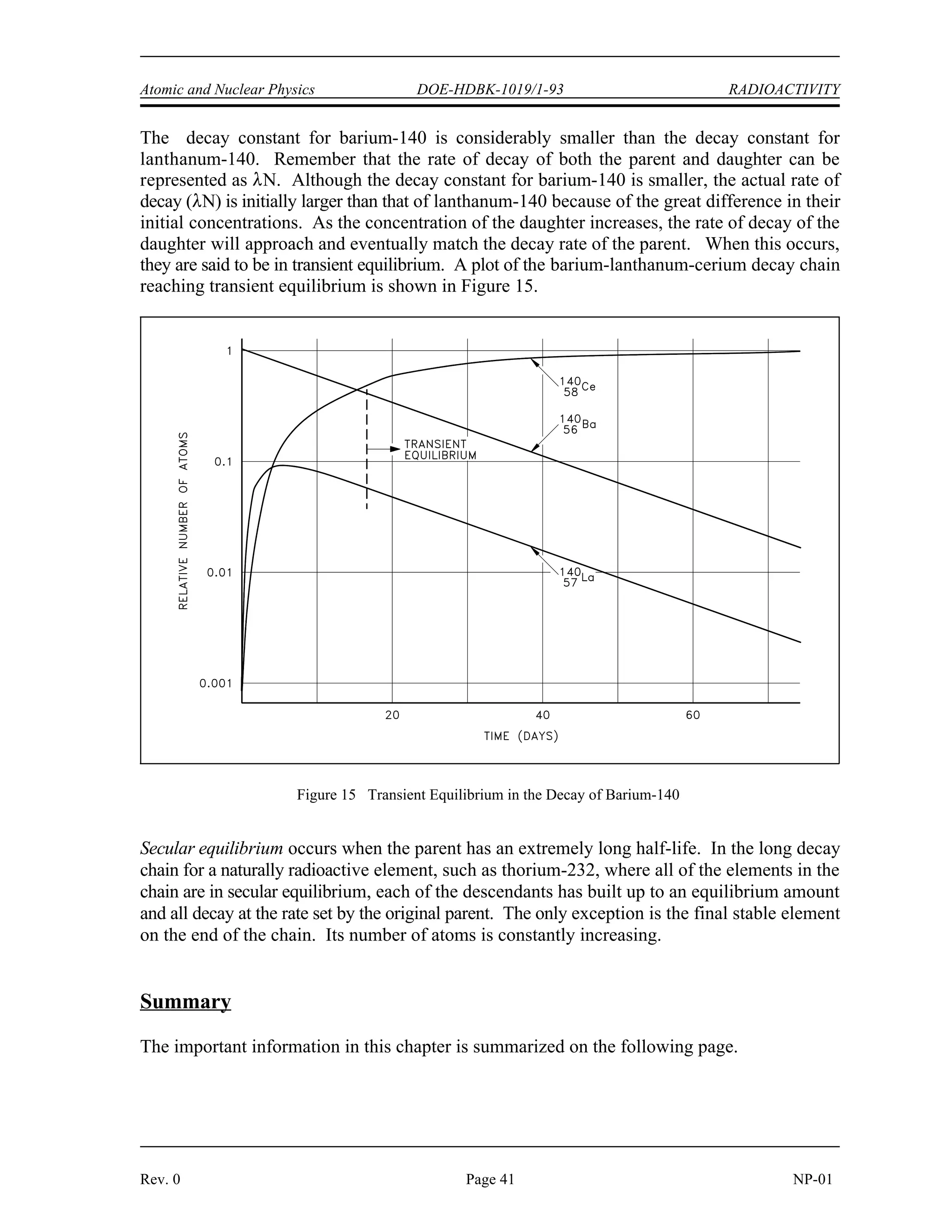
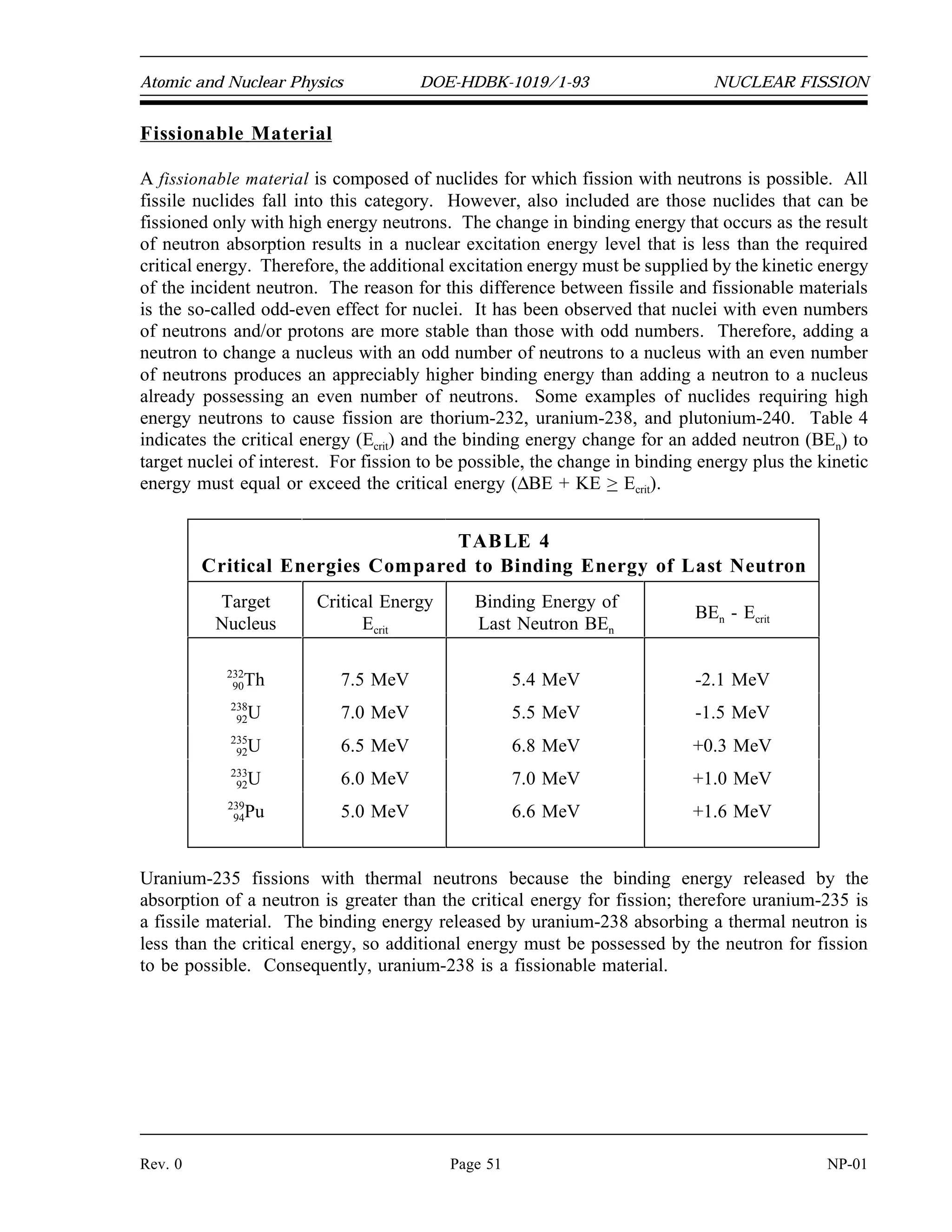
The document provides an overview of atomic and nuclear physics concepts. It discusses the atomic structure of matter, including subatomic particles and the Bohr model of the atom. It also covers the chart of nuclides, mass defect and binding energy, modes of radioactive decay including alpha, beta, gamma emission and electron capture. Additionally, it summarizes key topics in radioactivity such as decay rates, half-life and equilibrium. Neutron interactions like scattering and absorption reactions are also briefly described. The goal is to introduce fundamental physics principles relevant to nuclear processes and radiation.

































![Atomic and Nuclear Physics DOE-HDBK-1019/1-93 MASS DEFECT AND BINDING ENERGY
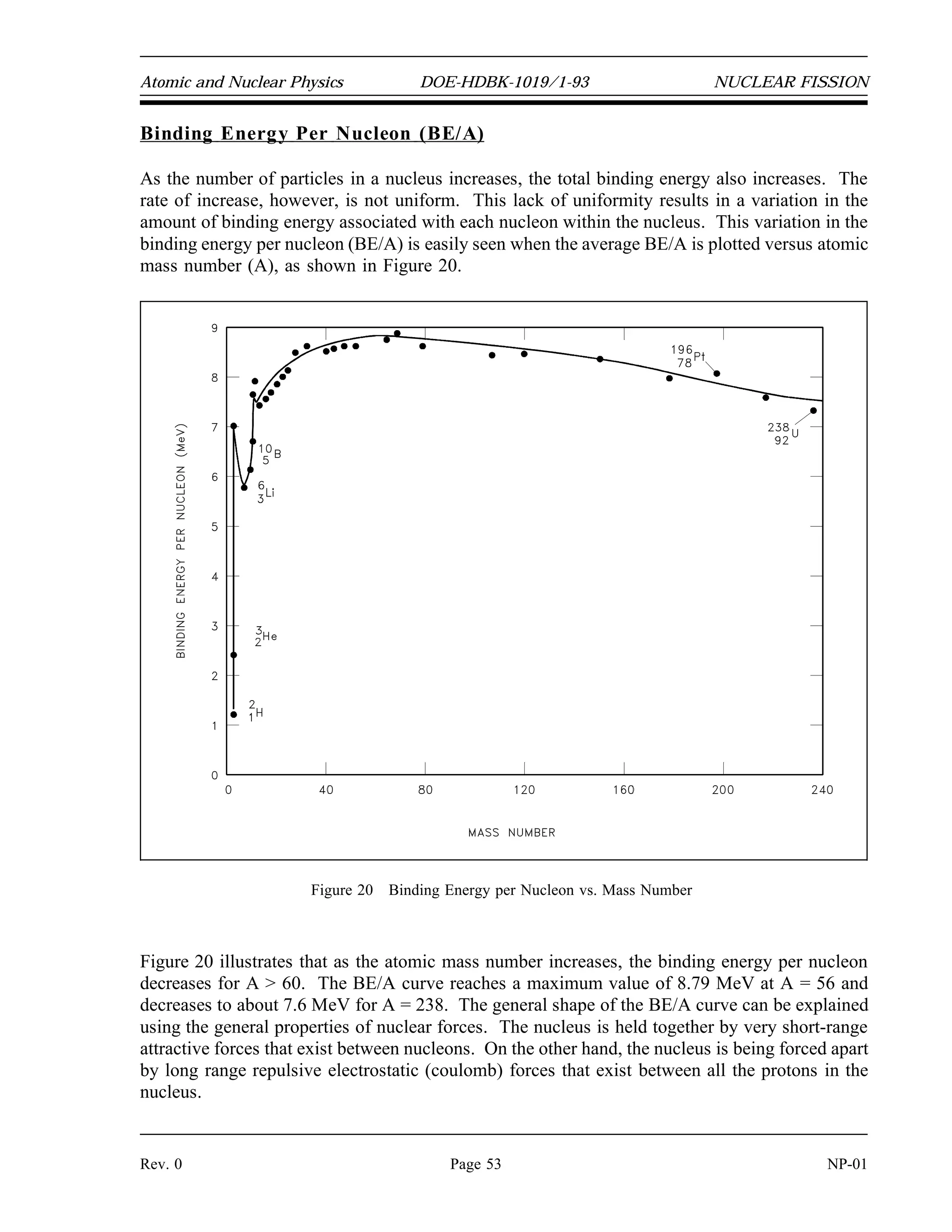
MASS DEFECT AND BINDING ENERGY
The separate laws of Conservation of Mass and Conservation of Energy are not
applied strictly on the nuclear level. It is possible to convert between mass and
energy. Instead of two separate conservation laws, a single conservation law
states that the sum of mass and energy is conserved. Mass does not magically
appear and disappear at random. A decrease in mass will be accompanied by a
corresponding increase in energy and vice versa.
EO 1.7 DEFINE the following terms:
a. Mass defect
b. Binding energy
EO 1.8 Given the atomic mass for a nuclide and the atomic masses of
a neutron, proton, and electron, CALCULATE the mass defect
and binding energy of the nuclide.
Mass Defect
Careful measurements have shown that the mass of a particular atom is always slightly less than
the sum of the masses of the individual neutrons, protons, and electrons of which the atom
consists. The difference between the mass of the atom and the sum of the masses of its parts is
called the mass defect (∆m). The mass defect can be calculated using Equation (1-1). In
calculating the mass defect it is important to use the full accuracy of mass measurements because
the difference in mass is small compared to the mass of the atom. Rounding off the masses of
atoms and particles to three or four significant digits prior to the calculation will result in a
calculated mass defect of zero.
∆m = [ Z(mp + me) + (A-Z)mn ] - matom (1-1)
where:
∆m = mass defect (amu)
mp = mass of a proton (1.007277 amu)
mn = mass of a neutron (1.008665 amu)
me = mass of an electron (0.000548597 amu)
matom = mass of nuclide A
ZX (amu)
Z = atomic number (number of protons)
A = mass number (number of nucleons)
Rev. 0 Page 17 NP-01](https://image.slidesharecdn.com/nuclearphysicsandreactortheory-220506033827-c5b2e1a6/75/NUCLEAR-PHYSICS-AND-REACTOR-THEORY-pdf-35-2048.jpg)



![Atomic and Nuclear Physics DOE-HDBK-1019/1-93 MASS DEFECT AND BINDING ENERGY
Summary
The important information in this chapter is summarized below.
Mass Defect and Binding Energy Summary
Mass defect is the difference between the mass of the atom and the sum of the
masses of its constituent parts.
Binding energy is the amount of energy that must be supplied to a nucleus to
completely separate its nuclear particles. Binding energy is the energy equivalent
of the mass defect.
Mass defect can be calculated by using the equation below.
∆m = [ Z(mp + me) + (A-Z)mn ] - matom
Binding energy can be calculated by multiplying the mass defect by the factor
of 931.5 MeV per amu.
Rev. 0 Page 21 NP-01](https://image.slidesharecdn.com/nuclearphysicsandreactortheory-220506033827-c5b2e1a6/75/NUCLEAR-PHYSICS-AND-REACTOR-THEORY-pdf-39-2048.jpg)



























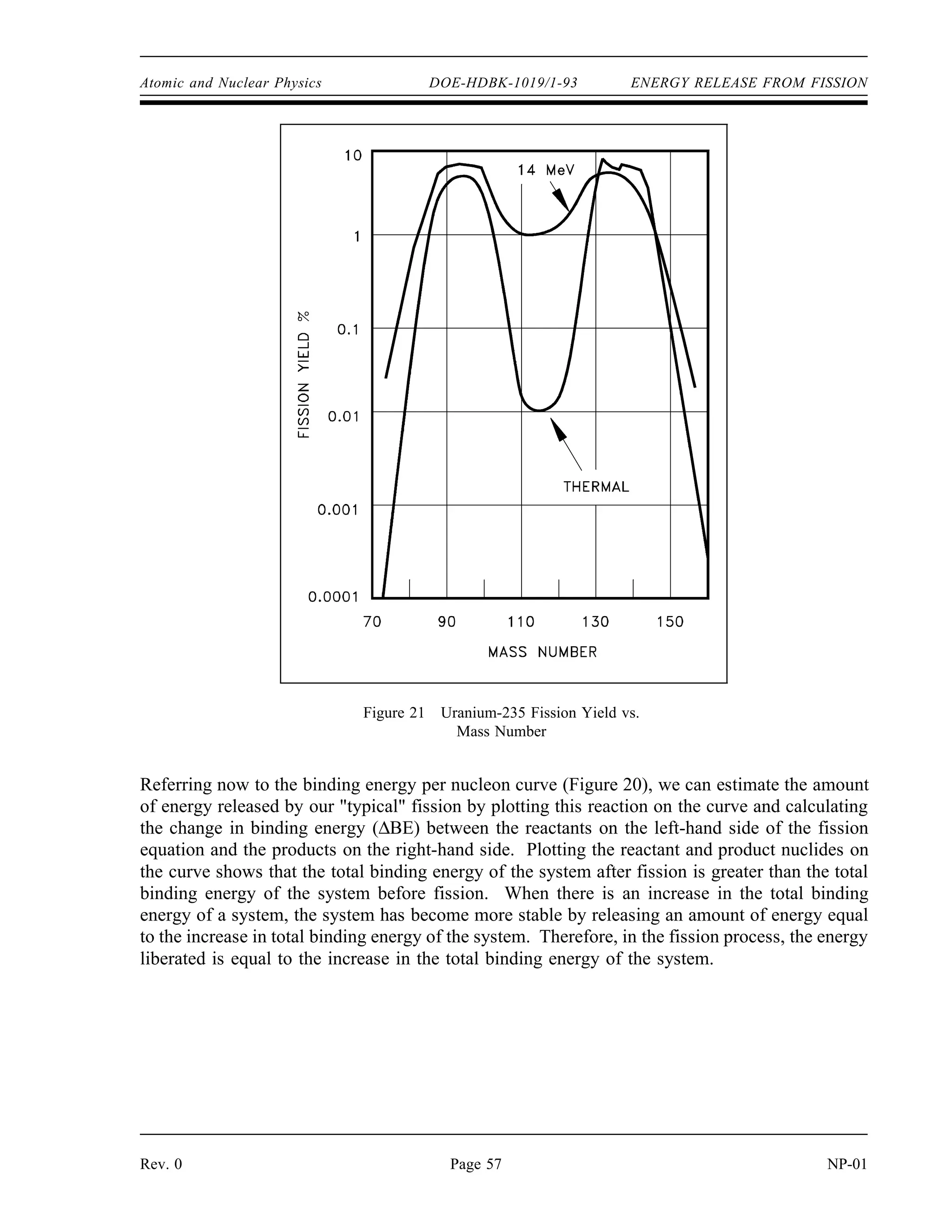
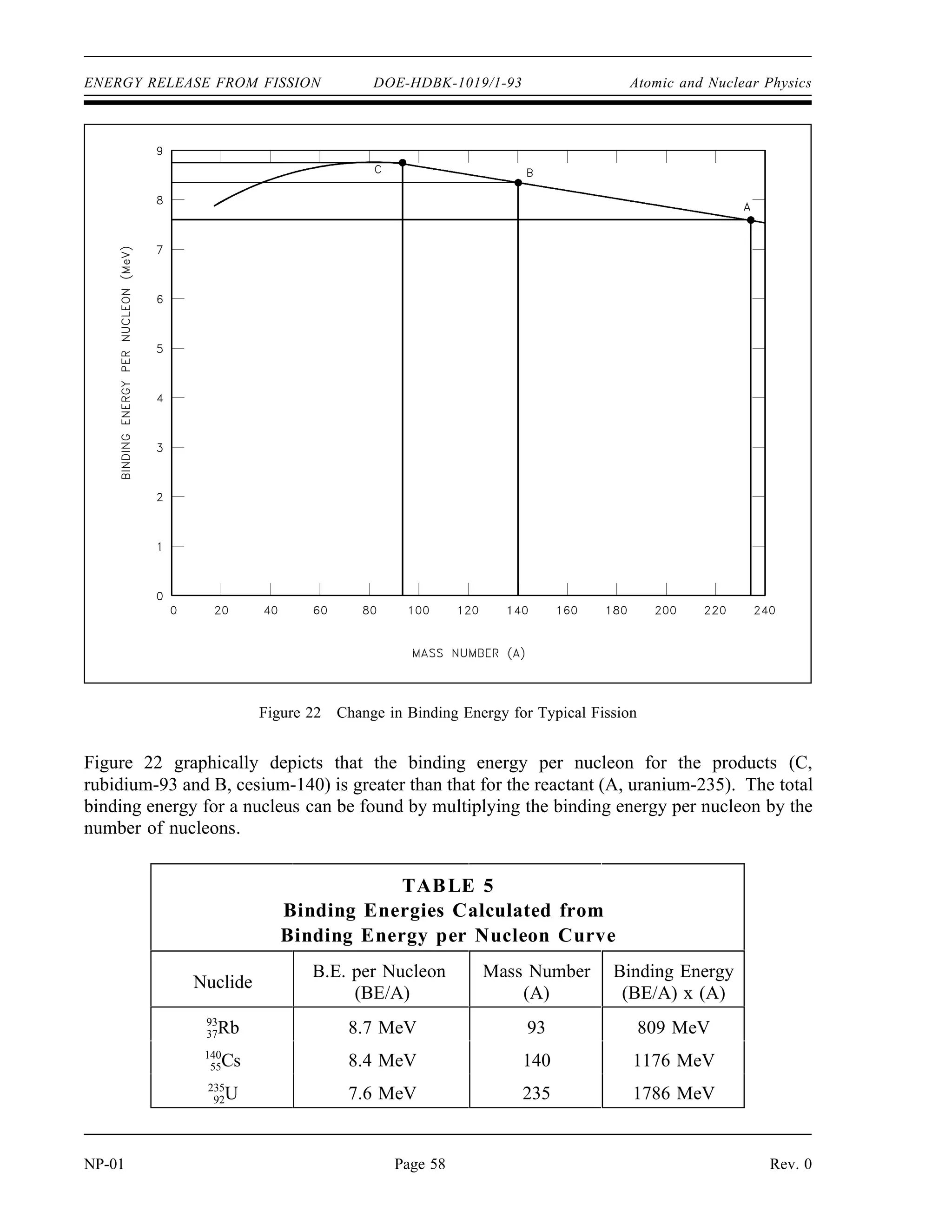
































![(
DOE-HDBK-1019/1-93
NUCLEAR CROSS SECTIONS AND NEUTRON FLUX Reactor Theory (Neutron Characteristics)
NP-02 Page 10 Rev. 0
Assuming that uranium-236 has a nuclear quantum energy level at 6.8 MeV above its ground
state, calculate the kinetic energy a neutron must possess to undergo resonant absorption in
uranium-235 at this resonance energy level.
BE = [Mass( U) + Mass(neutron) - Mass( U)] x 931 MeV/amu
235 236
BE = (235.043925 + 1.008665 - 236.045563) x 931 MeV/amu
BE = (0.007025 amu) x 931 MeV/amu = 6.54 MeV
6.8 MeV - 6.54 MeV = 0.26 MeV
The difference between the binding energy and the quantum energy level equals the amount of
kinetic energy the neutron must possess. The typical heavy nucleus will have many closely-
spaced resonances starting in the low energy (eV) range. This is because heavy nuclei are
complex and have more possible configurations and corresponding energy states. Light nuclei,
being less complex, have fewer possible energy states and fewer resonances that are sparsely
distributed at higher energy levels.
For higher neutron energies, the absorption cross section steadily decreases as the energy of the
neutron increases. This is called the fast neutron region. In this region the absorption cross
sections are usually less than 10 barns.
With the exception of hydrogen, for which the value is fairly large, the elastic scattering cross
sections are generally small, for example, 5 barns to 10 barns. This is close to the magnitude
of the actual geometric cross sectional area expected for atomic nuclei. In potential scattering,
the cross section is essentially constant and independent of neutron energy. Resonance elastic
scattering and inelastic scattering exhibit resonance peaks similar to those associated with
absorption cross sections. The resonances occur at lower energies for heavy nuclei than for light
nuclei. In general, the variations in scattering cross sections are very small when compared to
the variations that occur in absorption cross sections.
Mean Free Path
If a neutron has a certain probability of undergoing a particular interaction in one centimeter of
travel, then the inverse of this value describes how far the neutron will travel (in the average
case) before undergoing an interaction. This average distance traveled by a neutron before
interaction is known as the mean free path for that interaction and is represented by the symbol
. The relationship between the mean free path () and the macroscopic cross section (*) is
shown below.
(2-3)](https://image.slidesharecdn.com/nuclearphysicsandreactortheory-220506033827-c5b2e1a6/75/NUCLEAR-PHYSICS-AND-REACTOR-THEORY-pdf-109-2048.jpg)