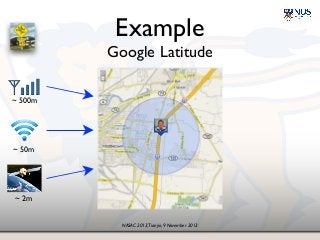
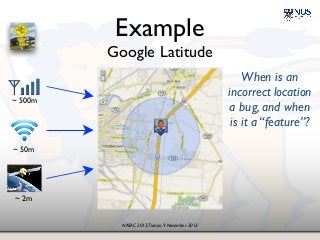
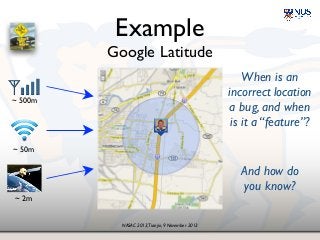
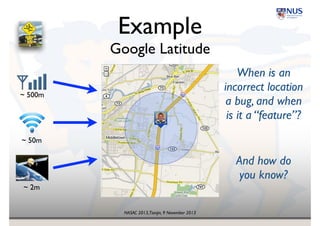
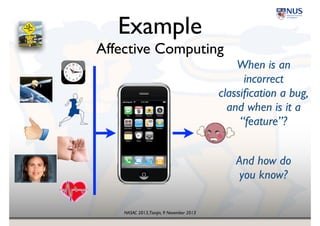
The document presents insights on probability and uncertainty in software engineering, emphasizing the limitations of traditional binary characterizations (correct/incorrect) and the necessity for probabilistic methods. It discusses various forms of uncertainty, including nondeterminism and empirical risk, and introduces probabilistic model checking as a tool for addressing such challenges. The conclusion highlights the need for a probabilistic mindset in software engineering to tackle inherent uncertainties.




![NASAC 2013,Tianjin, 9 November 2013
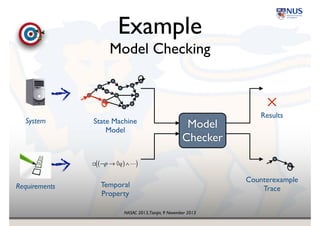
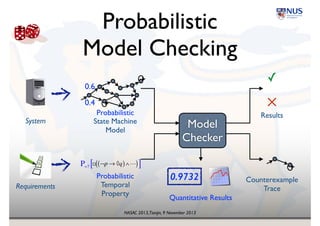
Probabilistic
Model Checking
! ¬p → ◊q( )∧"( )
Model
Checker
✓
✕
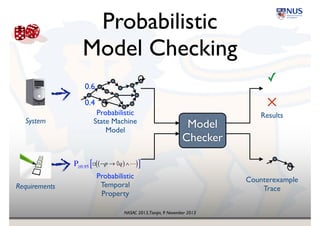
State Machine!
Model
Temporal
Property
Results
Counterexample!
Trace
System
Requirements
P≥0.95 [ ]
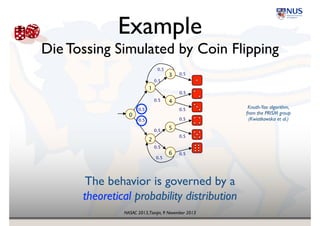
0.4
0.6
Probabilistic
Probabilistic](https://image.slidesharecdn.com/nasac2013-131112002838-phpapp02/85/Probability-and-Uncertainty-in-Software-Engineering-keynote-talk-at-NASAC-2013-9-320.jpg)
![NASAC 2013,Tianjin, 9 November 2013
Probabilistic
Model Checking
! ¬p → ◊q( )∧"( )
Model
Checker
✓
✕
State Machine!
Model
Temporal
Property
Results
Counterexample!
Trace
System
Requirements
P=? [ ]
0.4
0.6
Quantitative Results
0.9732Probabilistic
Probabilistic](https://image.slidesharecdn.com/nasac2013-131112002838-phpapp02/85/Probability-and-Uncertainty-in-Software-Engineering-keynote-talk-at-NASAC-2013-10-320.jpg)
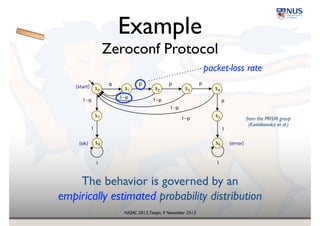

![NASAC 2013,Tianjin, 9 November 2013
Probabilistic
Model Checking
! ¬p → ◊q( )∧"( )
Model
Checker
✓
State Machine!
Model
Temporal
Property
Results
Counterexample!
Trace
System
Requirements
P≥0.95 [ ]
0.4
0.6
Quantitative Results
0.9732Probabilistic
Probabilistic](https://image.slidesharecdn.com/nasac2013-131112002838-phpapp02/85/Probability-and-Uncertainty-in-Software-Engineering-keynote-talk-at-NASAC-2013-13-320.jpg)
![NASAC 2013,Tianjin, 9 November 2013
Probabilistic
Model Checking
! ¬p → ◊q( )∧"( )
Model
Checker
✕
State Machine!
Model
Temporal
Property
Results
Counterexample!
Trace
System
Requirements
P≥0.95 [ ]
Quantitative Results
Probabilistic
Probabilistic
0.41
0.59
0.6211](https://image.slidesharecdn.com/nasac2013-131112002838-phpapp02/85/Probability-and-Uncertainty-in-Software-Engineering-keynote-talk-at-NASAC-2013-14-320.jpg)
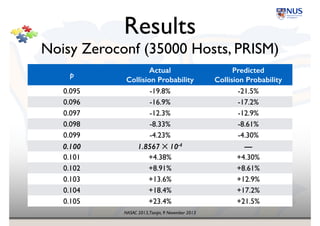



![NASAC 2013,Tianjin, 9 November 2013
Additional Aspects
• Models
✓Markov Decision Processes (MDPs)!
✓Continuous-Time Markov Chains (CMTCs)
• Verification
✓LTL Model Checking!
using Deterministic Rabin Automata!
✓PCTL Model Checking!
with singular perturbations due to nested P[ ] operators!
✓Reward Properties!
✓Alternative Norms and Bounds!
Kullback-Leibler Divergence, Quadratic Bounds](https://image.slidesharecdn.com/nasac2013-131112002838-phpapp02/85/Probability-and-Uncertainty-in-Software-Engineering-keynote-talk-at-NASAC-2013-21-320.jpg)