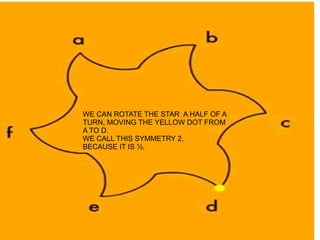
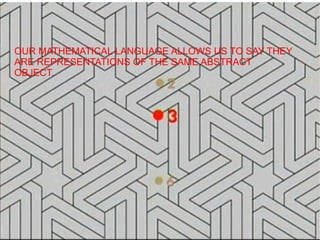
This document is about a young mathematician from Spain who created a mathematical language to classify symmetries. It discusses how he used this language to analyze patterns on the walls of the Alhambra in Granada. Different wall patterns that appear visually distinct are shown to have the same underlying rotational symmetries when analyzed using his mathematical notation. This language allowed classification of all possible surface symmetries into 17 types. The document poses a final mystery asking which symmetry type is represented in a particular pattern image.

1. MYSTERY #7 FROM SPAIN
M

2. WHO
WAS
I

3. I
WAS
A
MATHEMATICIAN

4. I CREATED A
LANGUAGE TO STUDY
SYMMETRY

5. I WAS KILLED IN A DUEL
WHEN I WAS ONLY TWENTY...

6. I COULD NOT SLEEP THAT NIGHT …
I WAS SURE IT WAS MY LAST ONE..
SO I SPENT THE WHOLE NIGHT
WRITING MY MATHEMATIC WILL...

7. MY LAST WORDS TO MY BROTHER WERE,
“DON'T CRY FOR ME, ALFRED.
I NEED ALL THE COURAGE I CAN MASTER
TO DIE AT THE AGE OF 20”

8. PART 2.
WHAT'S SYMMETRY FOR ME?
SYMMETRY IS MOTION.

9. WHO WROTE THIS FAMOUS QUOTATION?

10. IN THE ALHAMBRA OF GRANADA THERE IS SYMMETRY
EVERYWHERE. IMMEDIATELY YOU GO IN, YOU SEE THE
REFLECTIVE SYMMETRY IN THE WATER.

11. BUT IT IS MOTION WHAT REALLY CHARACTERIZES THE SYMMETRY
ON WALLS, FLOORS AND DOMES INSIDE THE ALHAMBRA .

12. HOW MANY TIMES CAN YOU MOVE A GEOMETRIC OBJECT
AROUND A TURNIG POINT SO THAT IT LOOKS EXACTLY
THE SAME AS BEFORE?

13. ON THE ALHAMBRA WALLS YOU CAN SEE THIS PATTERN.
FIND A POINT WHERE YOU CAN TURN IT BY 90 DEGREES AND
IT KEEPS THE SAME
.

14. PART 3.
HOW TO CLASSIFY
ALL THE POSSIBLE SYMMETRIES
IN THE ALHAMBRA?
CREATING A MATHEMATICAL LANGUAGE

15. LET'S TAKE A TWISTED SIX-
POINTED STARFISH.
WE CAN TURN THE STAR
A SIXTH OF A TURN, 1/6.

16. IF WE ROTATE THE YELLOW DOT FROM
A TO B, WE CALL THIS SYMMETRY
SIMPLY 6.
WE USE THE CENTRE OF THE STARFISH
AS THE ONLY AXIS.
IF WE ROTATE THE DOT BY A THIRD OF
A TURN, FROM A TO C, WE CALL IT 3,
IT IS 1/3.

17. WE CAN ROTATE THE STAR A HALF OF A
TURN, MOVING THE YELLOW DOT FROM
A TO D.
WE CALL THIS SYMMETRY 2,
BECAUSE IT IS ½.

18. IF WE TURN THE STAR FOUR-SIXTHS
OF A TURN, 4/6, WE ROTATE THE
YELLOW DOT FROM A TO E.
WE CALL IT 4.
IF WE ROTATE IT 5/6 OF A TURN, FROM A TO F,
WE CALL IT 5

19. WE CAN ROTATE THE STARFISH 360º,
WE NAME THIS SYMMETRY WITH THE
SYMBOL OF A STAR *.
NOW LET'S GO BACK TO THE
WALLS OF THE ALHAMBRA

20. WE CAN SEE TWO VERY DIFFERENT PATTERNS, BUT USING OUR LANGUAGE,
WE CAN UNDERSTAND THAT THE UNDERLYING ABSTRACT SYMMETRIES OF THESE
THINGS ARE ACTUALLY THE SAME,WITH THREE DIFFERENT AXIS OF ROTATION.

21. LET'S TAKE THIS WALL WITH THE
TWISTED TRIANGLES. THE SHAPES
MATCH IF WE ROTATE 180º, HALF OF A
TURN. IT HAS SYMMETRY NUMBER 2.

22. A THIRD OF A TURN AROUND THE CENTRE OF THE TRIANGLE
AND EVERYTHING MATCHES UP, IGNORING THE COLOURS.
THIS IS SYMMETRY NUMBER 3.

23. FINALLY, THE SHAPES MATCH
IF WE ROTATE BY A SIXTH OF A TURN.
IT HAS SYMMETRIES 2, 3, 6 AND *

24. LET'S MOVE TO A DIFFERENT WALL. WE FIND THE
SAME SYMMETRIES.
IT IS A SYMMETRY WE CALL 6-3-2.

25. OUR MATHEMATICAL LANGUAGE ALLOWS US TO SAY THEY
ARE REPRESENTATIONS OF THE SAME ABSTRACT
OBJECT.

26. DID THE MOORISH ARTISTS DICOVER ALL THE POSSIBLE
SYMMETRIES ON THE SURFACES OF THE ALHAMBRA?
THEY ALMOST DID. USING OUR LANGUAGE THEY ARE ONLY 17.

27. THE MYSTERY IS:
M
COULD YOU TELL US WHICH TYPE
OF SYMMETRY IS THERE IN THIS PATTERN?

28. WE HOPE YOU LIKE OUR MYSTERY

29. THANK YOU VERY MUCH!