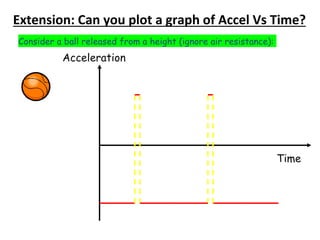
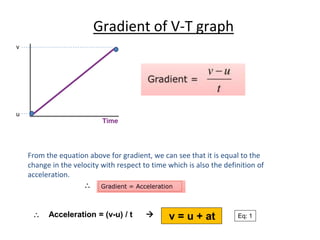
The document discusses motion graphs for a ball released from a height while ignoring air resistance. It first shows displacement-time and velocity-time graphs, then adds an acceleration-time graph. It explains that the gradient of the velocity-time graph equals acceleration. It also discusses how the area under velocity-time graphs relates to distance traveled for constant velocity and constant acceleration motion.

1. 1.3 Mechanics
2.1 Equations of motion
Learning outcomes
1
Use graphical methods to represent distance, displacement, speed, velocity
and acceleration
2
Use graphical methods to analyse distance, displacement, speed, velocity
and acceleration

2. A closer look at motion graphs
(Consider a ball released from a height )
Displacement
Time

3. A closer look at motion graphs
Consider a ball released from a height :
Displacement
Time

4. Recall: Velocity-Time Graphs

5. A closer look at motion graphs
Consider a ball released from a height (Ignore Air resistance!)
Velocity
Time

6. A closer look at motion graphs
Velocity
Time
Consider a ball released from a height (Ignore Air resistance!)

7. Acceleration
Time
Extension: Can you plot a graph of Accel Vs Time?
Consider a ball released from a height (Ignore Air resistance!)

8. Extension: Can you plot a graph of Accel Vs Time?
Consider a ball released from a height (ignore air resistance):
Acceleration
Time

9. Gradient of V-T graph
From the equation above for gradient, we can see that it is equal to the
change in the velocity with respect to time which is also the definition of
acceleration.
v
u

 Acceleration = (v-u) / t  v = u + at Eq: 1

10. Area under V-t graph (constant velocity)
To find the area under the graph shown is:
area = height x base
area = velocity x time
However, recall that  Distance = Velocity x time
 Area under VT graph = Total distance travelled

11. Area under V-t graph (constant acceln)
To find the area under the graph shown:
Notes shape is a trapezium
area = ½ (A+B) x base
area = ½ (u + v) x time
Since Area under VT graph = Total distance travelled
We can say S = ½ (u + v) x t Eq: 2