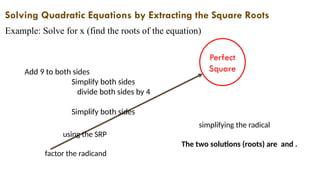
This document outlines methods for solving quadratic equations, including extracting square roots, factoring, completing the square, and using the quadratic formula. It provides examples and rules, such as the square root principle, alongside practice activities for students. By the end of the session, students are expected to master these techniques for determining the roots of quadratic equations.

1. SOLVING QUADRATIC EQUATIONS

2. Learning Objective
At the end of the session, student should be able to solve quadratic equations by:
a. Extracting Square Roots
b. Factoring
c. Completing the Square
d. Quadratic Formula

3. Solving Quadratic Equations
Ways to solve quadratic equations. (solve for x or finding the roots of the
equation)
1. Extracting the Square Roots
2. Factoring
3. Completing the Square
4. Using Quadratic Formula
5. Graphing

4. KICKSTARTER: Know My Values
Find the values of a, b and c in the following quadratic equations. (page 10)

5. Solving Quadratic Equations by Extracting the Square Roots
Rule: The Square Root Principle (SRP)
If

6. Solving Quadratic Equations by Extracting the Square Roots
Example: Solve for x (find the roots of the equation)
using the SRP
simplifying the radical
The two solutions (roots) are 2 and - 2.

7. Solving Quadratic Equations by Extracting the Square Roots
Example: Solve for x (find the roots of the equation)
using the SRP
simplifying the radical
The two solutions (roots) are 7 and - 7.

8. Solving Quadratic Equations by Extracting the Square Roots
Example: Solve for x (find the roots of the equation)
Subtracting 3 to both sides
Simplify both sides
using the SRP
factor the radicand
simplifying the radical
The two solutions (roots) are and .
Perfect
Square

9. Solving Quadratic Equations by Extracting the Square Roots
Example: Solve for x (find the roots of the equation)
Perfect
Square
Add 9 to both sides
Simplify both sides
divide both sides by 4
Simplify both sides
using the SRP
factor the radicand
simplifying the radical
The two solutions (roots) are and .

10. Solving Quadratic Equations by Extracting the Square Roots
Example: Solve for x (find the roots of the equation)
isolate the term containing quadratic
apply the square root property
simplify the radical
isolate the variable x
𝒙𝟏=𝟓+𝟏𝟎=𝟏𝟓
𝒙𝟐=𝟓 −𝟏𝟎=−𝟓
The roots are -5 and 15.

11. Solving Quadratic Equations by Extracting the Square Roots
Example: Solve for x (find the roots of the equation)
isolate the term containing quadratic
apply the square root property
simplify the radical
isolate the variable x
𝒙 𝟏=𝟐+𝟐 √𝟑
𝒙 𝟐=𝟐 −𝟐 √𝟑
The roots are
factor the radical
Perfect
Square

12. Solving Quadratic Equations by Extracting the Square Roots
Example: Solve for x (find the roots of the equation)
using the SRP
add 3 to both sides
simplify both sides
divide both sides by 5
simplify both sides
𝒙=
𝟑± √𝟏𝟔 √− 𝟐
𝟓
𝒙=
𝟑 ± 𝟒 √−𝟐
𝟓
Because the square root of a
negative number is not a real
number, there is no real number to
the given equation.

13. Activity: It’s in My Roots!!
Solve the following quadratic equations (pages 12-13).