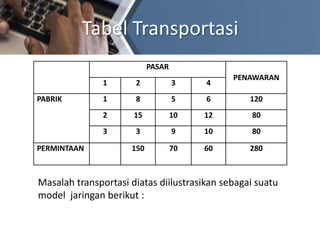
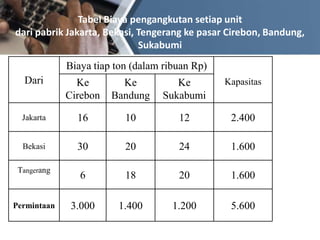
Model transportasi menggunakan metode North West Corner untuk mengalokasikan sumber daya dari beberapa pabrik ke beberapa gudang dengan mempertimbangkan kapasitas pabrik, permintaan gudang, dan biaya transportasi. Metode ini mengisi tabel alokasi dengan memulai dari sel paling kiri atas sesuai kapasitas dan permintaan, lalu mengisi sel-sel berikutnya hingga terpenuhi. Contoh menunjukkan alokasi produk dari 3 pabrik

1. MODEL
TRANSPORTASI
( Metode North West Corner )

2. Pengertian Metode Transportasi
Metode ransportasi merupakan bagian
dari Linier Programing (LP) yang
digunakan untuk mengatur dan
mendistribusikan sumber-sumber yang
menyediakan produk-produk ke tempat-
tempat yang membutuhkan untuk
mencapai efisiensi biaya transportasi.

3. Alokasi produk harus
memperhatikan biaya distribusi dari
satu tempat ke tempat yang lain,
hal ini dikarenakan adanya
perbedaan dari biaya-biaya
tersebut.

4. Syarat Metode Transportasi
• Besarnya kebutuhan (permintaan)
sama dengan kapasitas
• Apabila kebutuhan tidak sama
dengan kapasitas maka untuk
menyamakan ditambahkan
variable dummy dengan biaya
distribusi sebesar 0 (nol).

5. Data Untuk model Transportasi
1) Tingkat persediaan atau kapasitas
atau penawaran dari masing-
masing sumber atau asal dan
banyaknya kebutuhan atau
permintaan dari masing-masing
tujuan.
2) Satuan biaya transportasi untuk
mengangkut komoditas tersebut
dari masing-masing sumber ke
masing-masing tujuan.

6. Tujuan Model Transportasi
Menentukan banyaknya
komoditas yang harus
diangkut dari setiap sumber
ke masing-masing tujuan
sedemikian hingga total
biaya transportasi
minimum.

7.  Terdapat sejumlah sumber dan tujuan
tertentu.
 Kuantitas komoditi/barang yang
didisitribusikan dari setiap sumber
dan yang diminta oleh setiap tujuan
besarnya tertentu.
 Komoditi yang dikirim/diangkut dari
suatu sumber ke suatu tujuan
besarnya sesuai dengan permintaan
dan atau kapasitas sumber.
 Ongkos pengangkutan komoditi dari
suatu sumber ke suatu tujuan
besarnya tertentu.
Ciri-ciri Penggunaan Metode
Transporatasi

8. Contoh Model Transportasi
Suatu produk yang dihasilkan
pada tiga pabrik (sumber) dan
harus distribusikan ke tiga
gudang (tujuan) seperti
ditunjukkan pada gambar
berikut.

9. • Pabrik (Sumber) Gudang (Tujuan)
CIREBON
BANDUNG
CILACAP
SEMARANG
JAKARTA
PURWOKERTO

10. Masalah Transportasi Seimbang
• Masalah transportasi seimbangan
dimana jumlah supply dari semua
sumber sama dengan jumlah
permintaan pada semua tempat
tujuan.
• Slide berikut contoh masalah
transportasi seimbang

11. Contoh
• Sebuah perusahaan negara
berkepentingan mangangkut pupuk
dari tiga pabrik ke tiga pasar. Kapasitas
Supply ketiga pabrik, permintaan pada
ketiga pasar dan biaya transport per
unit adalah sebagai berikut (slide
berikut )

12. Tabel Transportasi
PASAR
PENAWARAN
1 2 3 4
PABRIK 1 8 5 6 120
2 15 10 12 80
3 3 9 10 80
PERMINTAAN 150 70 60 280
Masalah transportasi diatas diilustrasikan sebagai suatu
model jaringan berikut :

13. 13
Pabrik Gudang
Permintaa
n
Kapasita
s
P1
P2
P3
G
1
G
2
G
3
80
120
80
70
150
60
Representasi Dalam Bentuk Jaringan
8
5
6
15
10
12
3
9
10
Bagaimana menentukan alokasi agar di dapat biaya yang minimum (termurah) ?!
Metode apa saja yang dapat di pergunakan ?!

14. Ada 3 metode untuk mencari solusi awal atau
Tabel Awal (feasible awal)
 Aturan NWC (North West Corner)
 Metode INSPEKSI (Ongkos terkecil)
 Metode VAM (Vogel Approkximation Method)
Tabel Optimum (Menentukan solusi feasible
optimal)
 Metode Steppingstone (batu loncatan)
 Metode MODI (Modified Distribution)
Metode Pemecahan Masalah

15. 1. Metode North West Corner (NWC/ Sudut Barat Daya )
Langkah-langkah Metode Sudut Barat Laut :
1. Membuat table transportasi
2. Dimulai dari sel sudut kiri atas yang diisi dengan angka
sebanyak-banyak yang disesuaikan dengan kapasitas
dan permintaan (pilih yang paling kecil)
3. Lakukan langkah yang sama pada langkah ke-2 diatas
untuk mengisi sel-sel lain yang disesuiakn dengan
kapasitas dan permintaan sampai seluruh kapasitas
dan permintaan terpenuhi.

16. • Suatu perusahaan yang mempunyai 3 buah
pabrik di Jakarta, Bekasi dan Tangerang dengan
kapasitas masing-masing 2.400, 1.600 dan 1.600
unit dan memiliki daerah pemasaran di
Cerebon, Bandung, dan Sukabumi dengan
permintaan masing-masing 3.000, 1.400 dan
1.200 uni. Biaya angkut per unit (dalam ribuan)
dari pabrik ke daerah pemasaran seperti yang
tertera pada table berikut
Contoh :

17. Tabel Kapasitas pabrik
Pabrik Kapasitas produksi
Jakarta 2.400 unit
Bekasi 1.600 unit
Tangerang 1.600 unit
Jumlah 5.600 unit

18. Tabel Kebutuhan gudang
Daerah Pemasaran Kebutuhan
Cirebon 3000 unit
Bandung 1.400 unit
Sukabumi 1.200 unit
Jumlah 5.600 unit

19. Tabel Biaya pengangkutan setiap unit
dari pabrik Jakarta, Bekasi, Tengerang ke pasar Cirebon, Bandung,
Sukabumi
Dari
Biaya tiap ton (dalam ribuan Rp)
Ke
Cirebon
Ke
Bandung
Ke
Sukabumi
Kapasitas
Jakarta 16 10 12 2.400
Bekasi 30 20 24 1.600
Tangerang
6 18 20 1.600
Permintaan 3.000 1.400 1.200 5.600

20. Penyusunan Tabel Alokasi
1. jumlah kebutuhan tiap-tiap pasar diletakkan pada baris
terakhir
2. kapasitas tiap pabrik pada kolom terakhir
3. biaya pengangkutan diletakkan pada segi empat kecil
Pasar Cirebon Pasar Bandung Pasar Sukabumi
Kapasitas
Pabrik
Pabrik
X11
16
X12
10
X13
12
2.400
Jakarta
Pabrik
X21
30
X22
20
X23
24
1.600
Bekasi
Pabrik
X31
6
X32
18
X33
20
1.600
Tangerang
Kebutuhan
Pasar
3.000 1.400 1.200 5.600
Ke
Dari
Aturan

21. PENYELESAIAN
Pasar Cirebon Pasar Bandung Pasar Sukabumi
Kapasitas
Pabrik
Pabrik
2.400
16
X
10
X
12
2.400
Jakarta
Pabrik
6.00
30
1.000
20
X
24
1.600
Bekasi
Pabrik
X
6
400
18
1.200
20
1.600
Tangerang
Kebutuhan
Pasar
3.000 1.400 1.200 5.600
Ke
Dari

22. PENJELASAN
a. Alokasi pertama pada sudut kiri atas sebesar
2.400 unit (kapasitas 2.400 unit dan permintaan
3.000 unit jadi pilih yang paling kecil)
b. Bekasi Cirebon sebesar 600 unit (kapasitas
1.600 unit dan permintaan 600 unit) selanjutnya
Bekasi-Bandung sebesar 1.000 unit (kapasitas
1000 unit dan permintaan 1.400 unit)
c. Tangerang-Bandung sebesar 400 unit (kapasitas
1.600 unit dan permintaan 400 unit)
d. Tangerang-Sukabumi sebesar 1.200 (kapasitas
sama dengan permintaan)

23. Alokasi Produk dari Pabrik ke daerah pemasaran menurut
metode sudut barat laut (north west corne rules) dan
biaya transportasinya sbb
Dari Ke Jumlah Biaya per
unit
Biaya (Rp)
Jakarta Cirebon 2.400 16.000 38.400.000
Bekasi Cirebon 600 30.000 18.000.000
Bekasi Bandung 1.000 20.000 20.000.000
Tangerang Bandung 400 18.000 7.200.000
Tangerang Sukabumi 1.200 20.000 24.000.000
Total Biaya 107.600.000

24. Dari