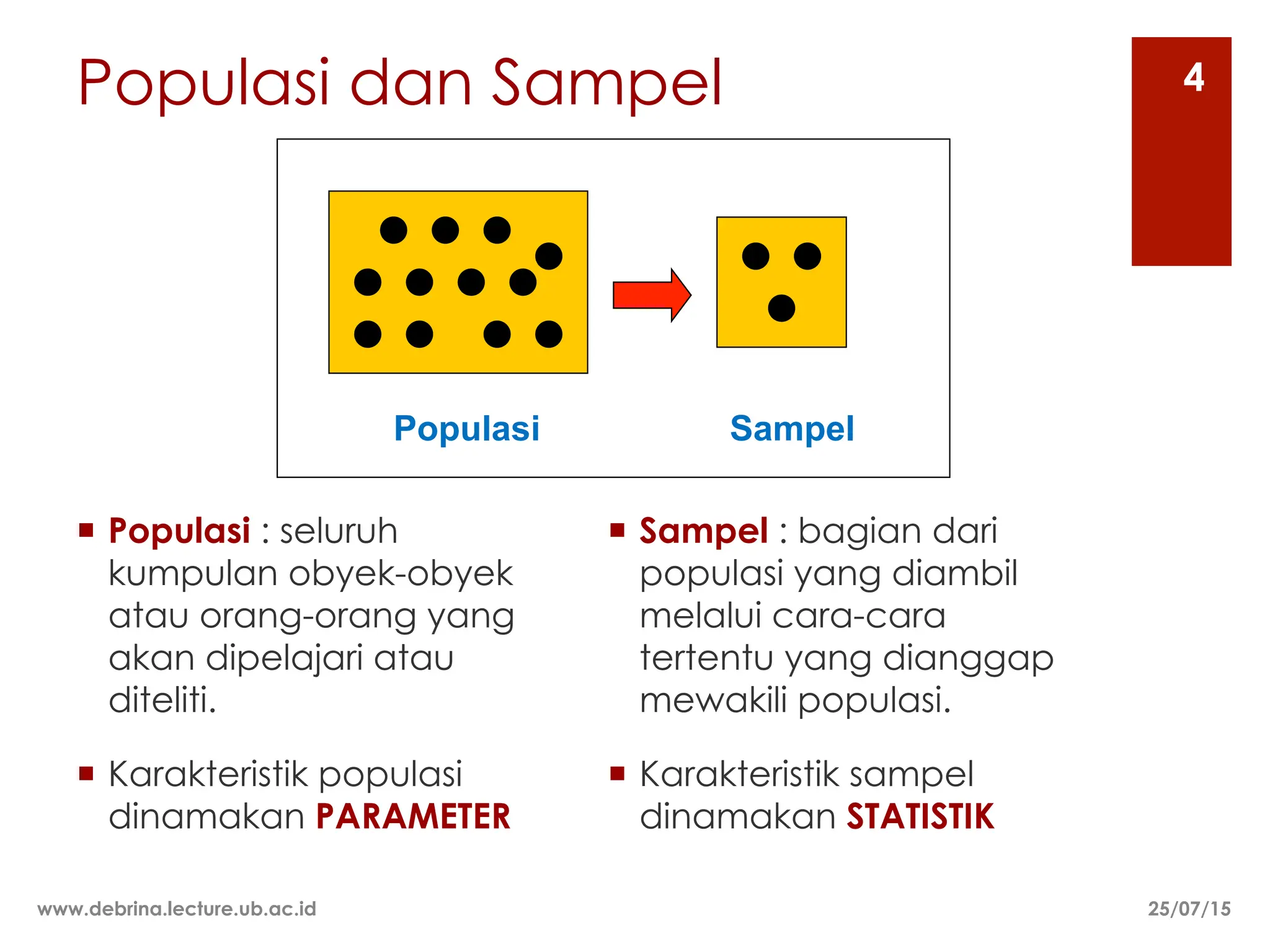
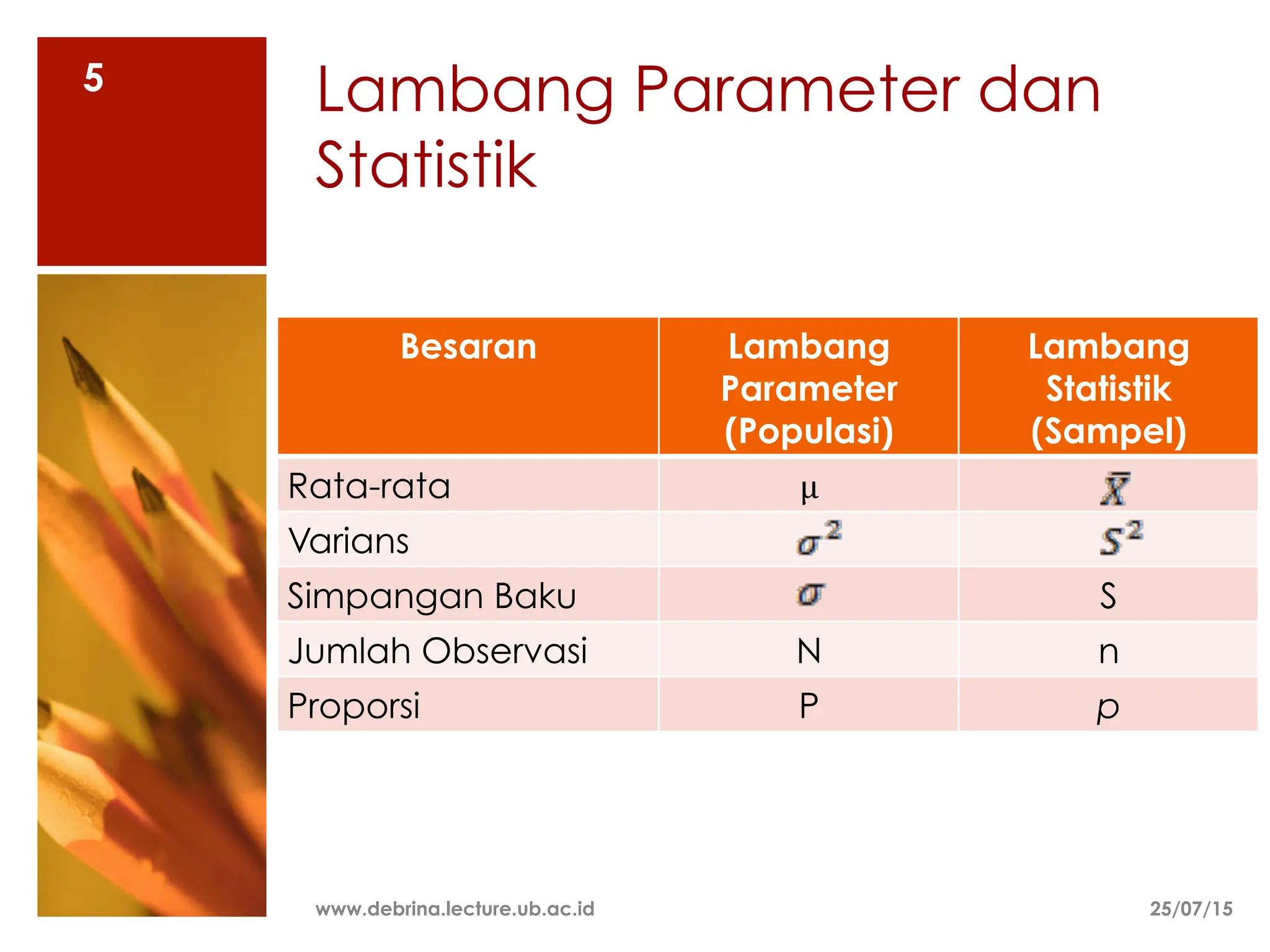
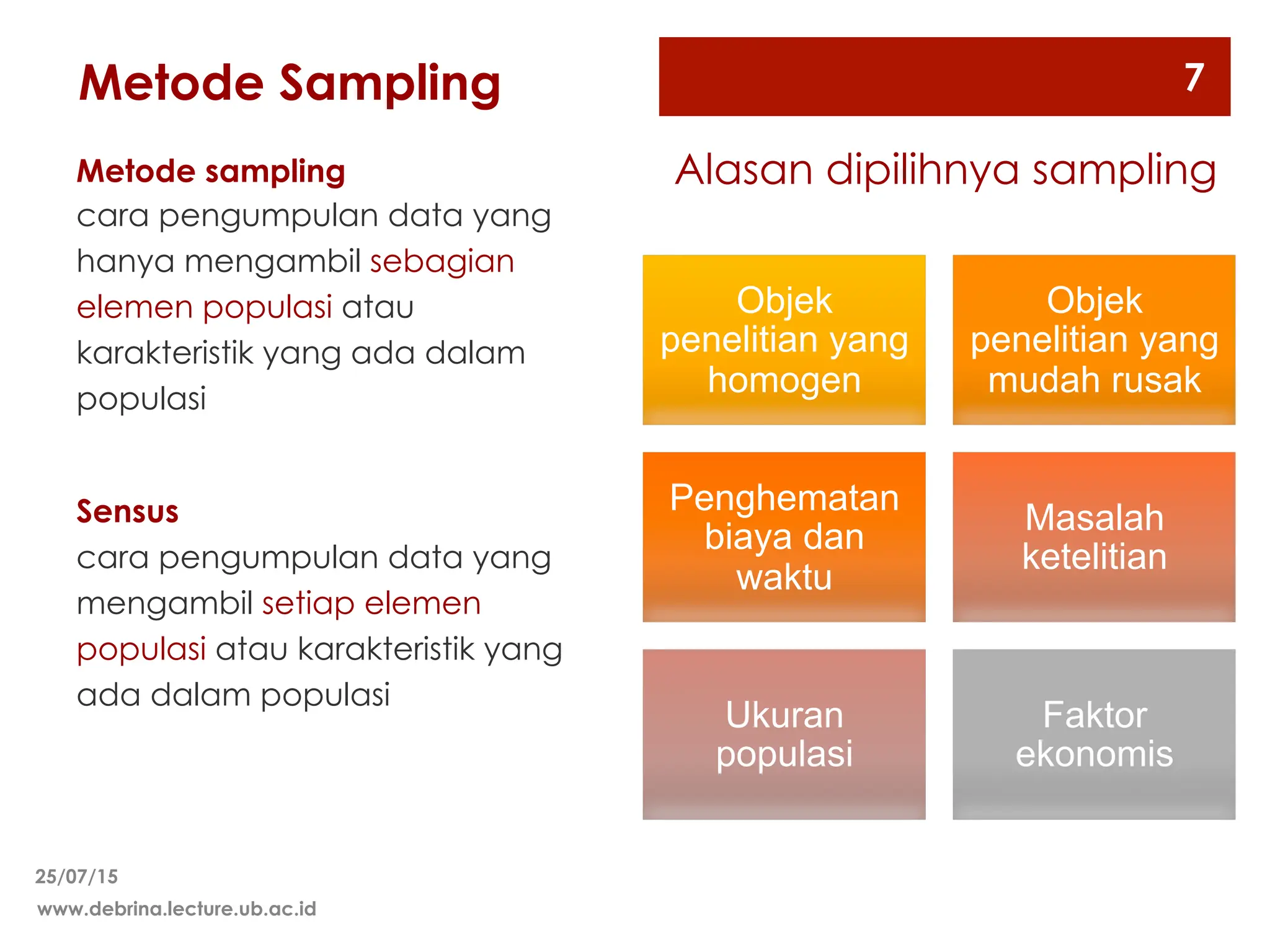
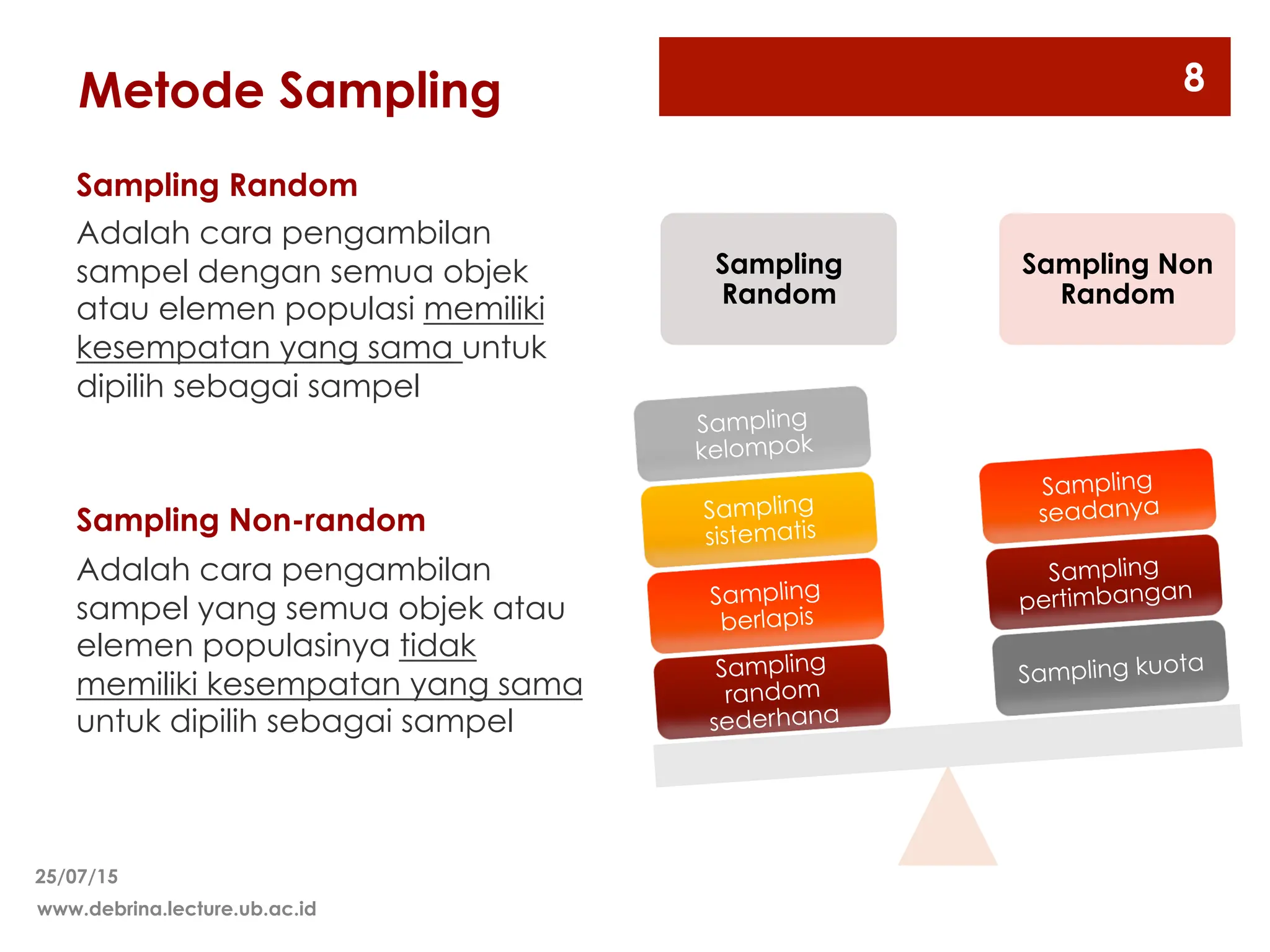
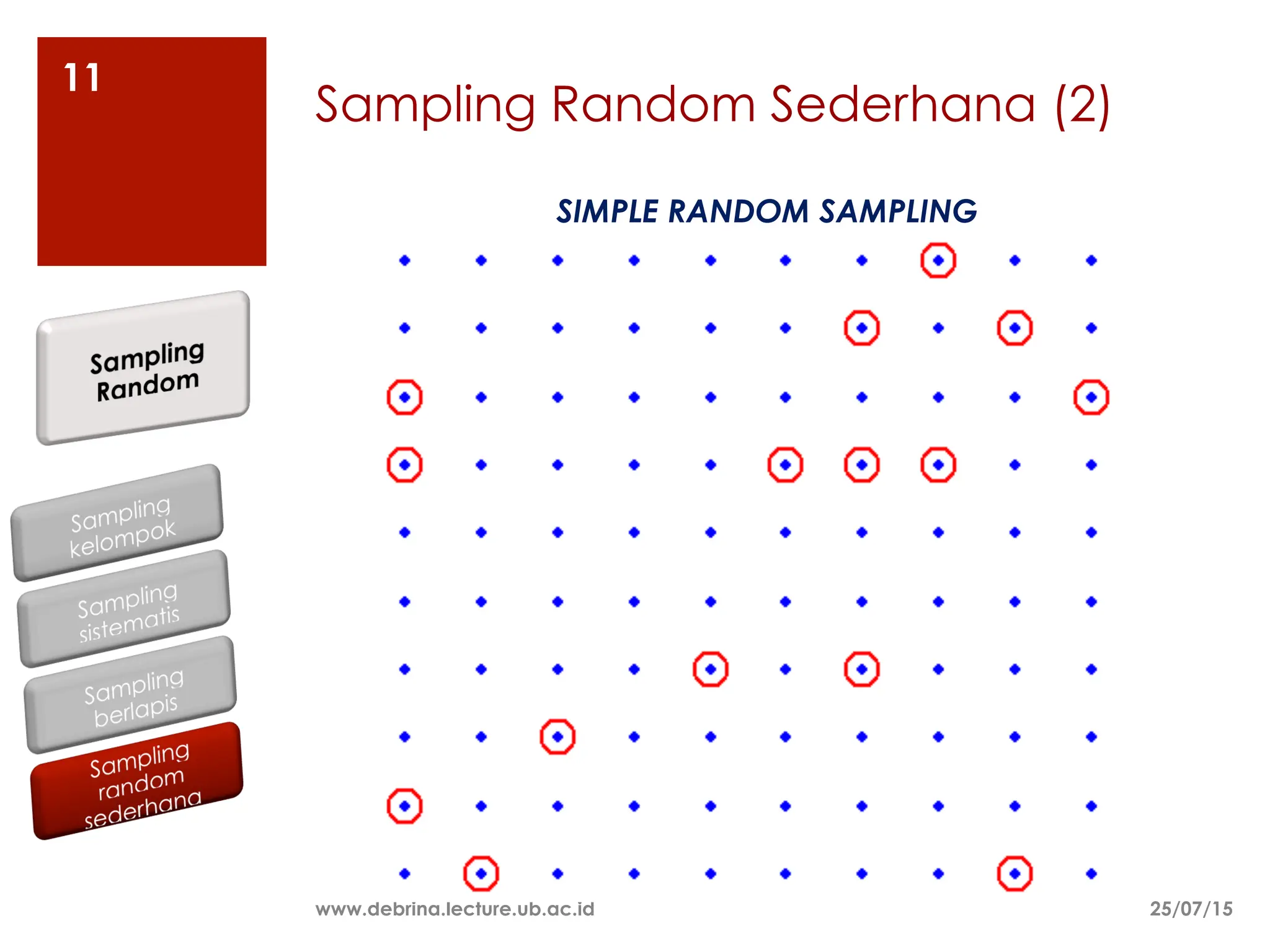
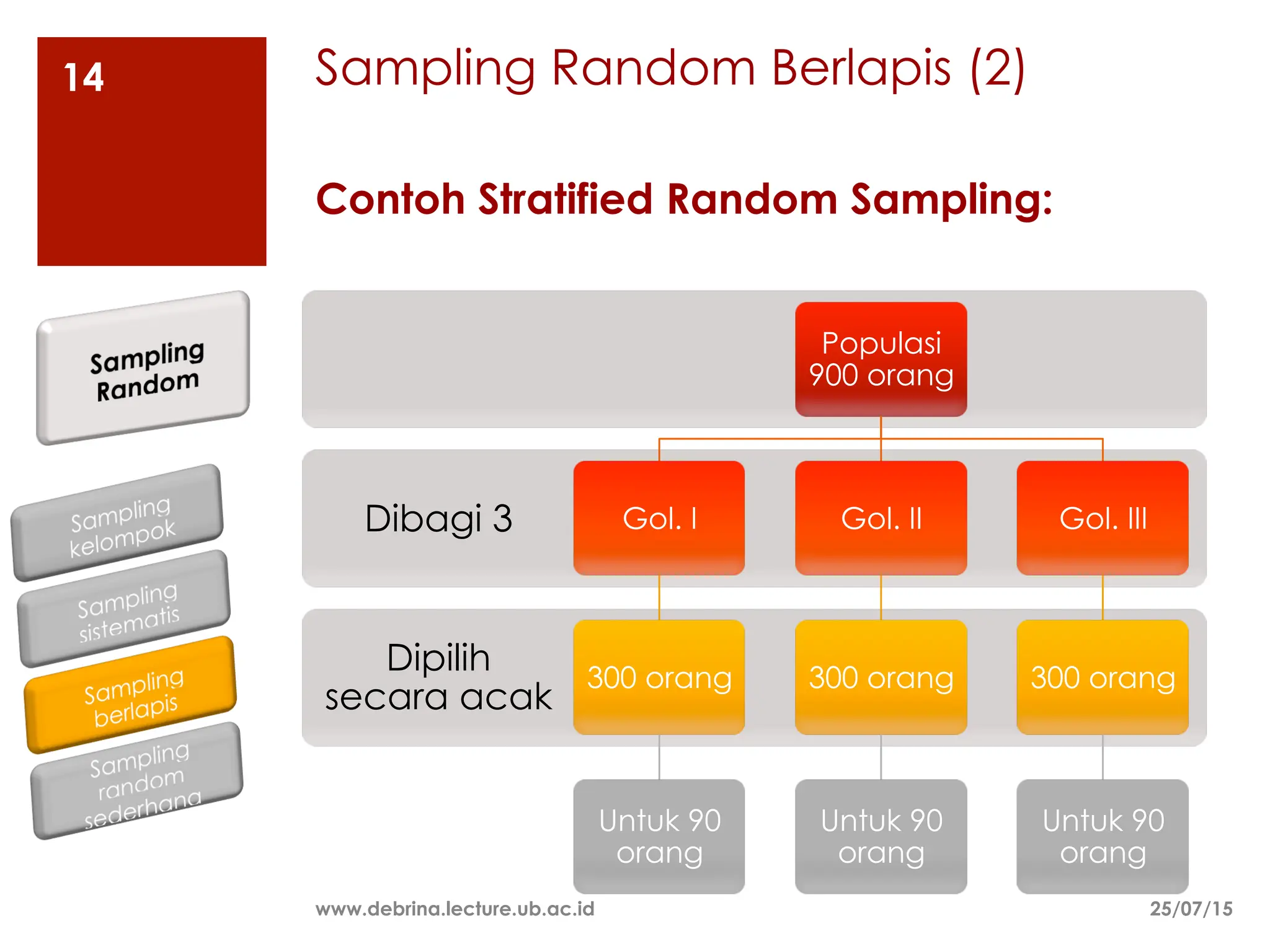
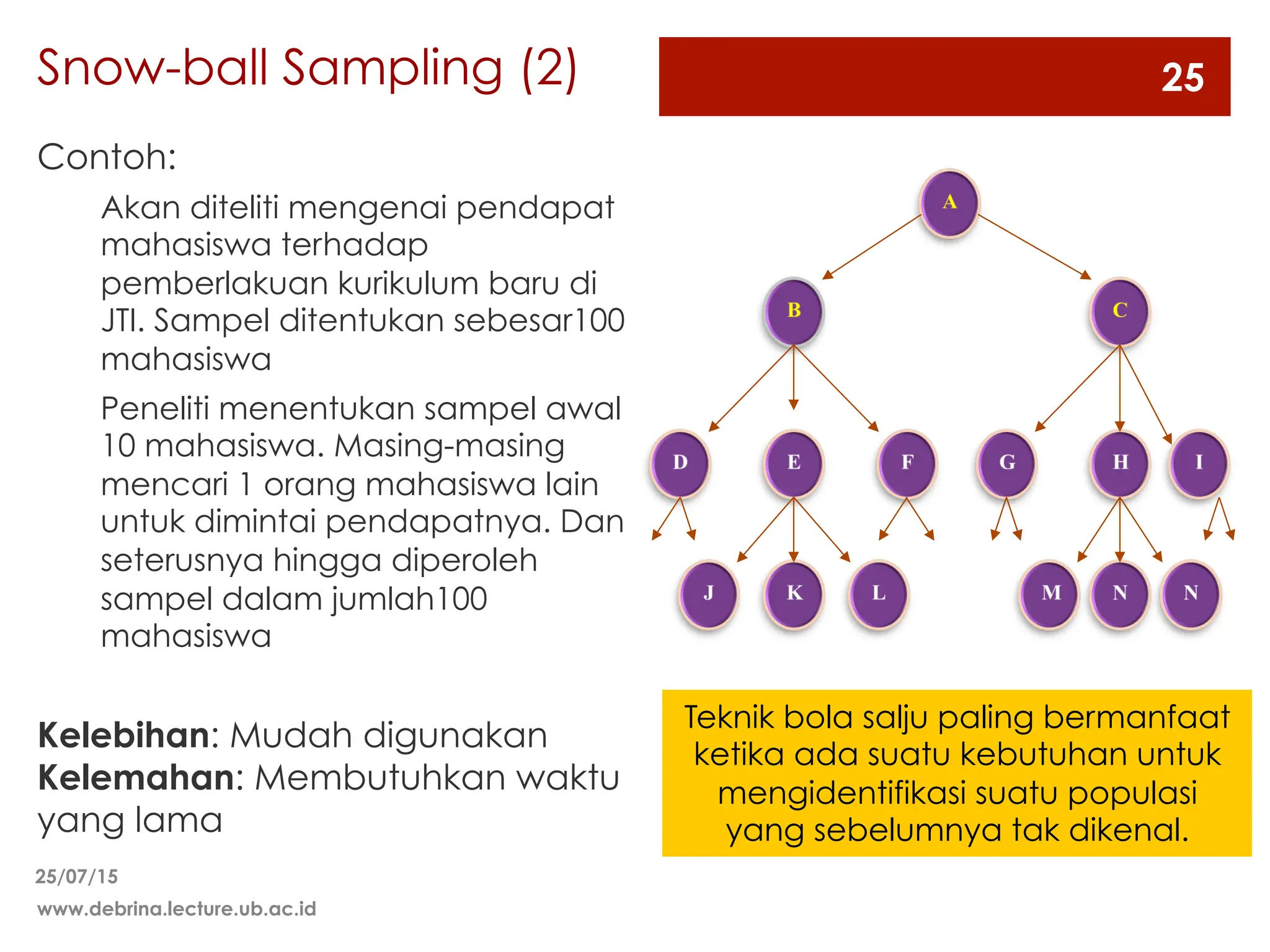
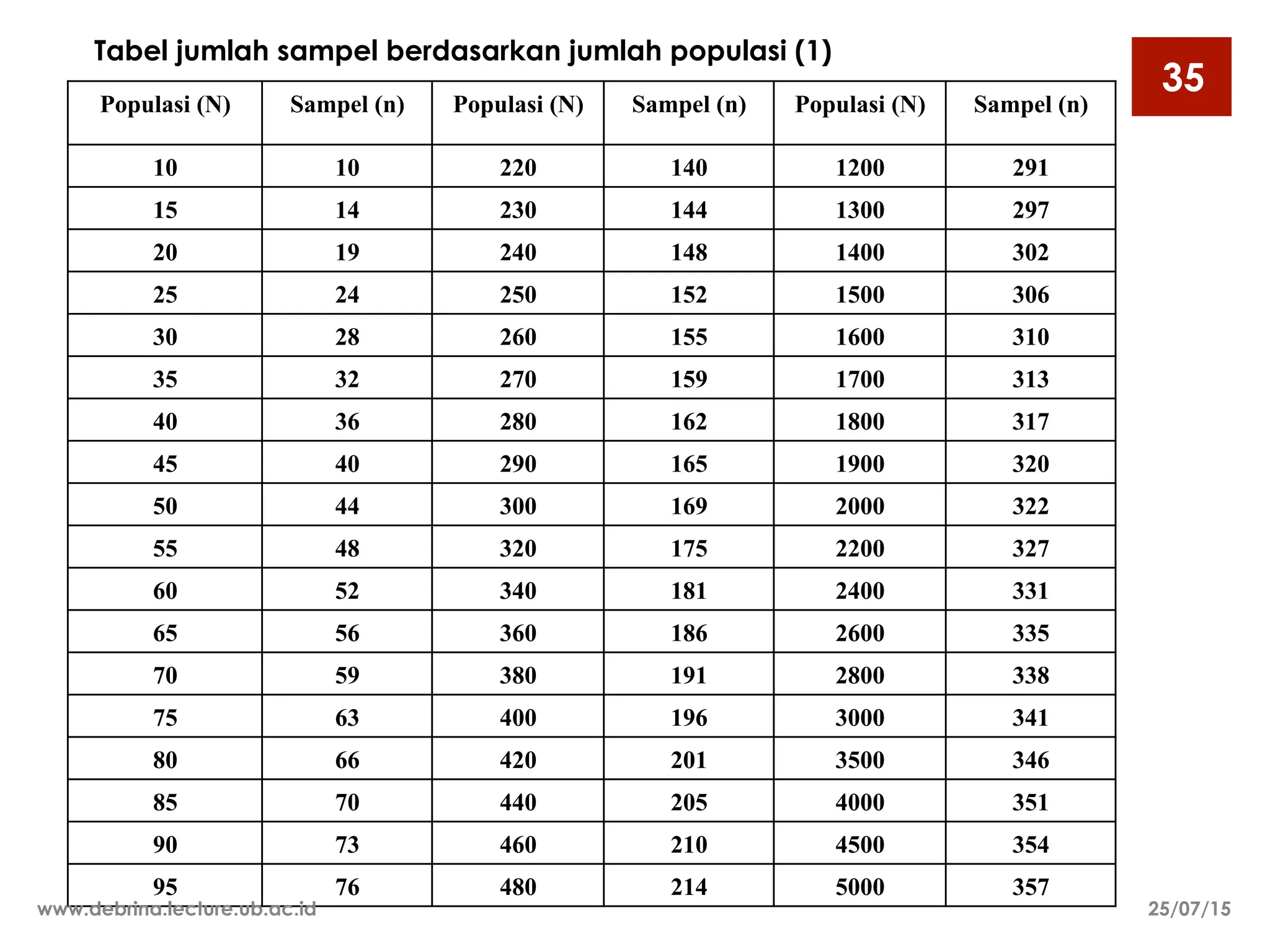
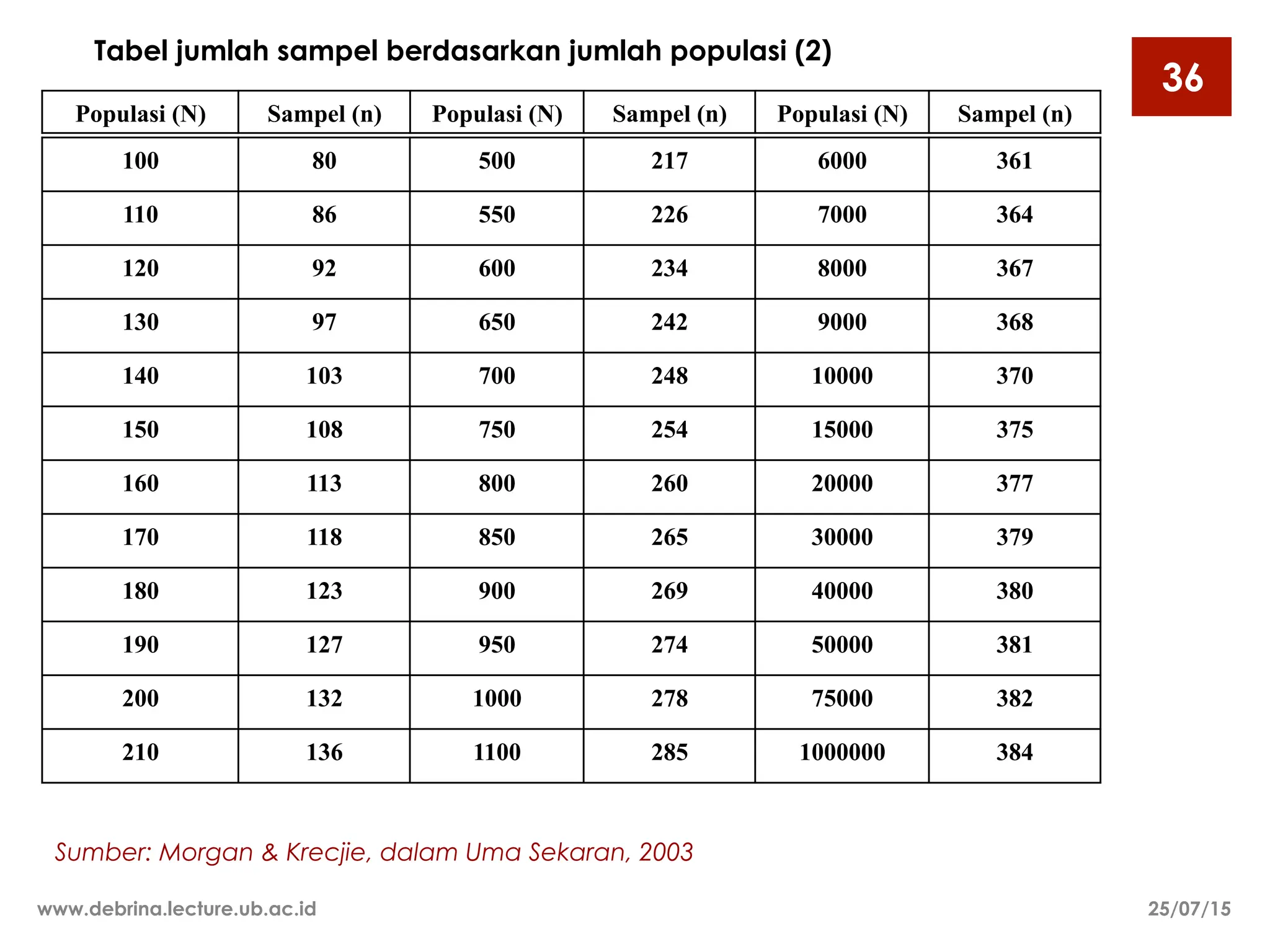
Dokumen ini membahas berbagai metode sampling, termasuk sampling random dan non-random, serta teknik-teknik yang digunakan untuk menentukan ukuran sampel yang representatif dari populasi. Metode sampling yang dijelaskan meliputi sampling random sederhana, stratified, sistematis, dan kelompok, serta sampling non-random seperti kuota dan seadanya. Selain itu, dokumen ini mencakup pertimbangan dalam menentukan ukuran sampel berdasarkan heterogenitas populasi, biaya, waktu, dan tingkat presisi yang diinginkan.