Downloaded 28 times
Uploaded byDr Nick Dalton
Merge sort b
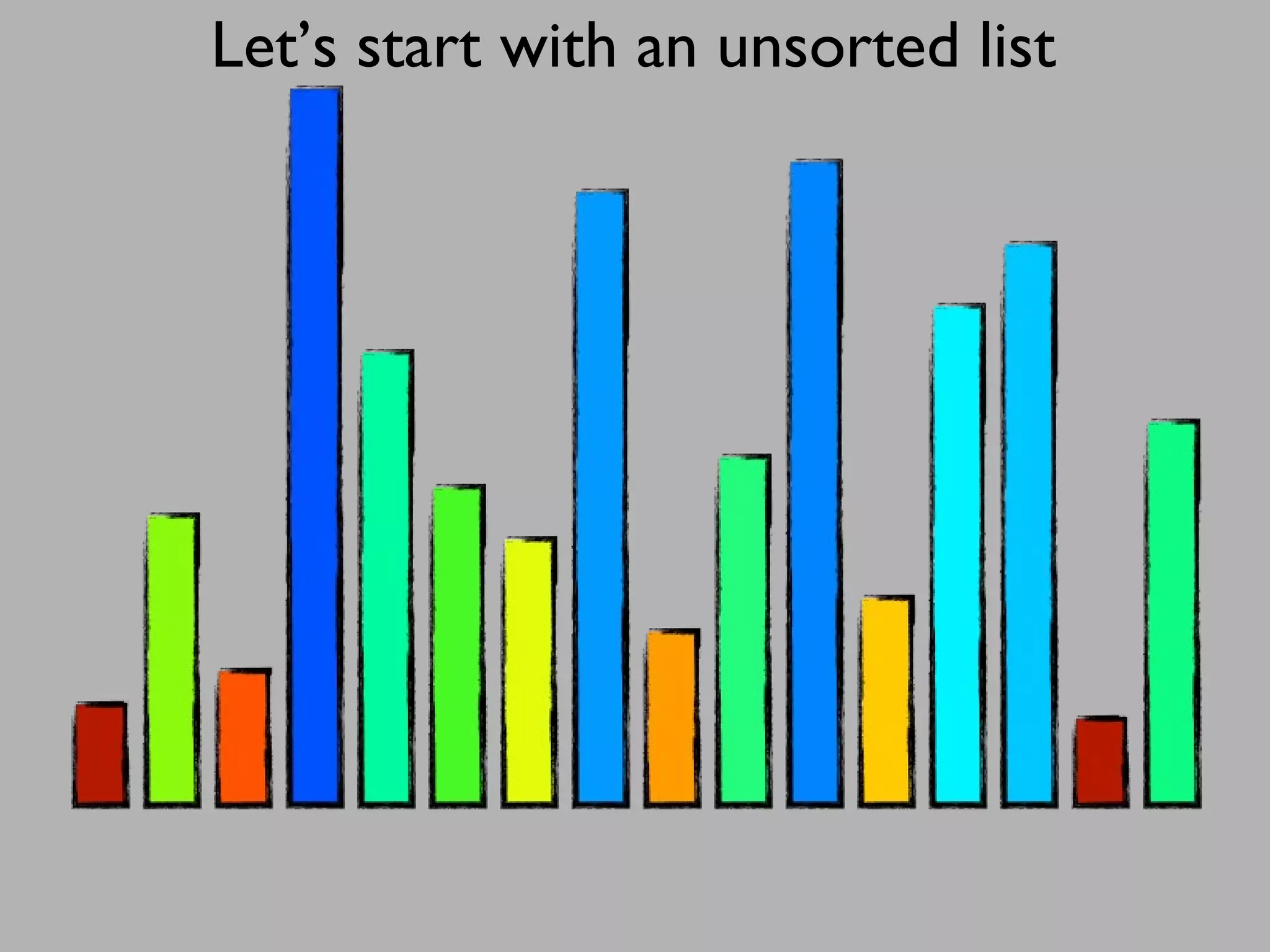
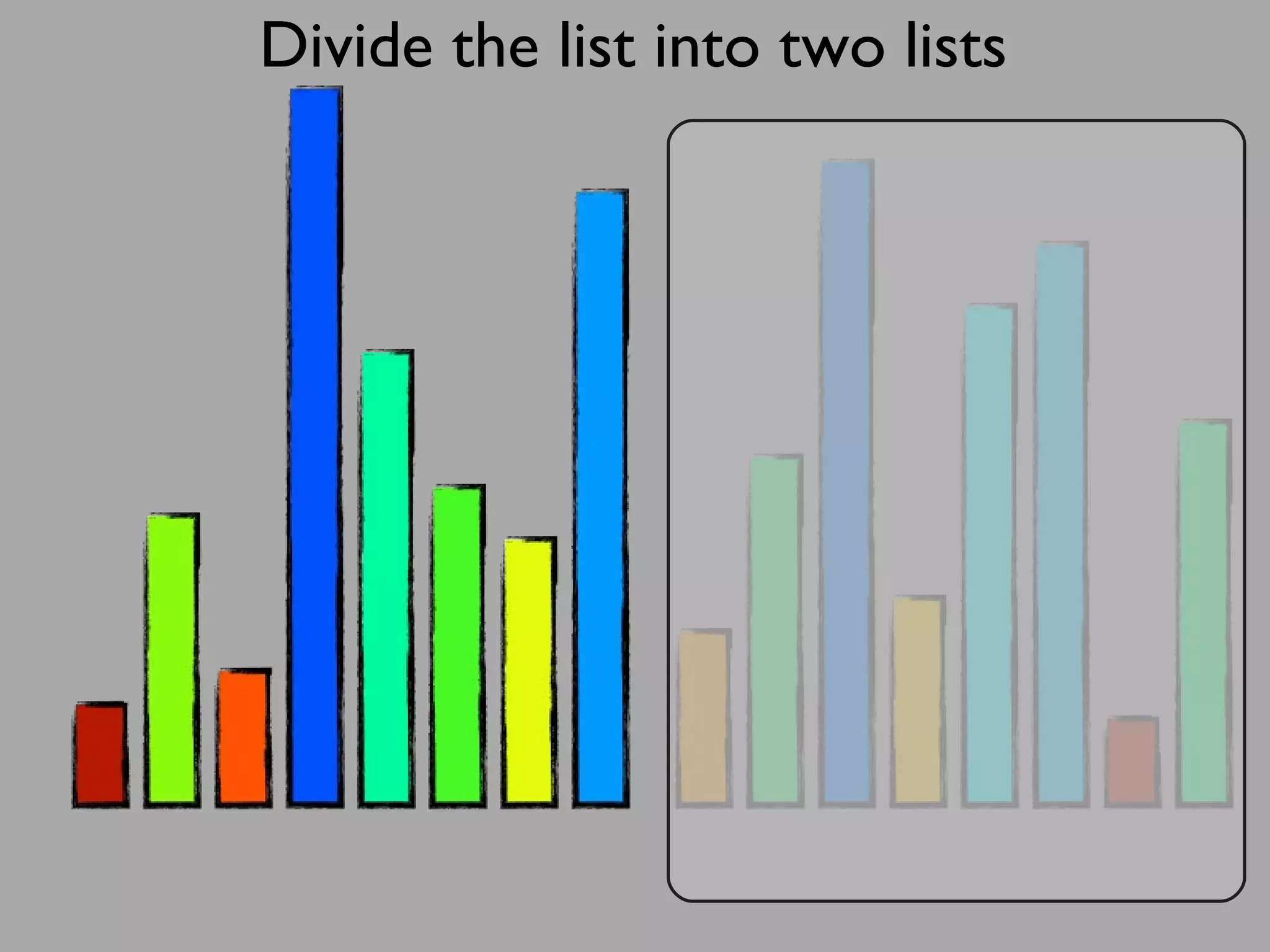
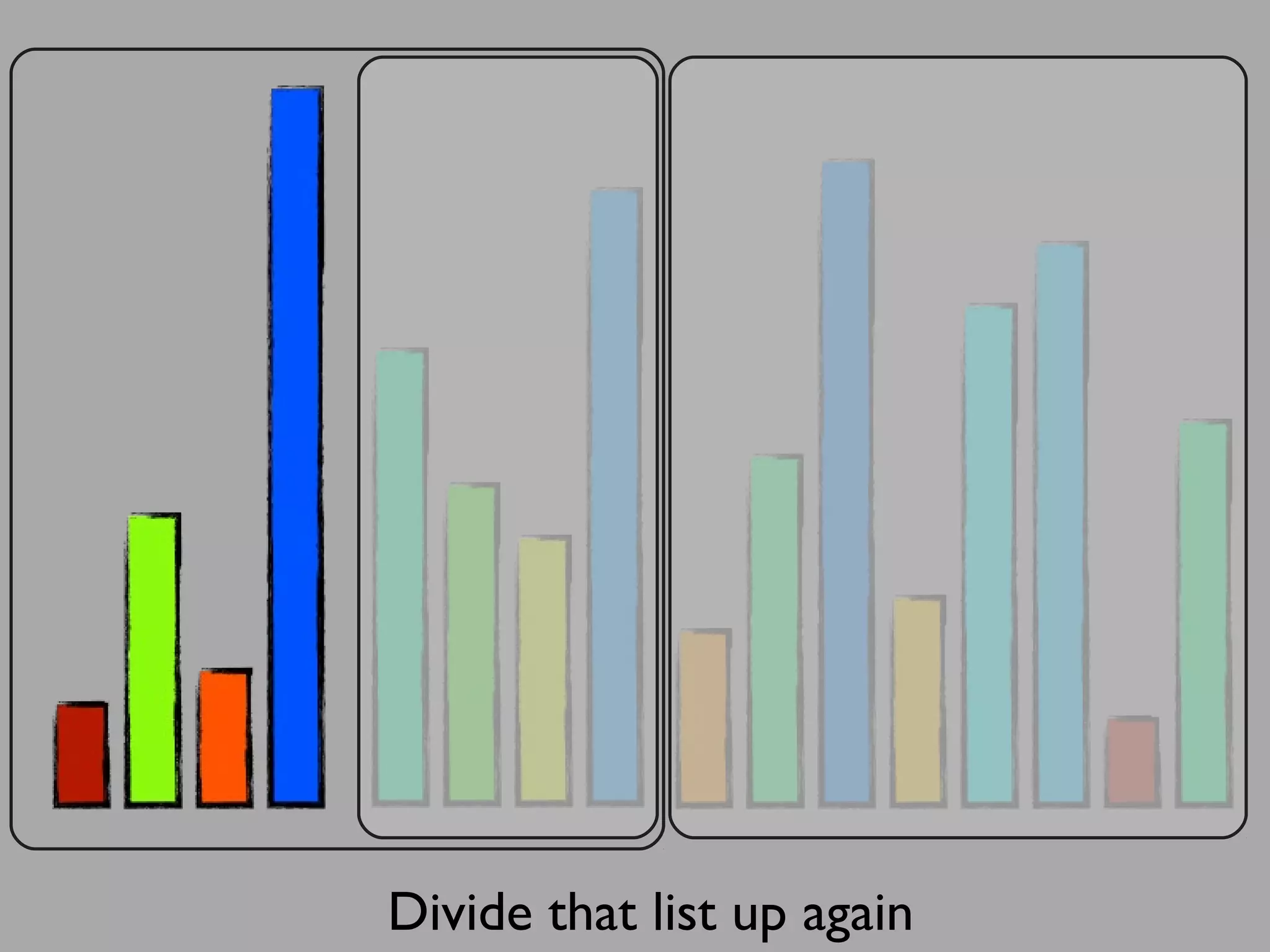
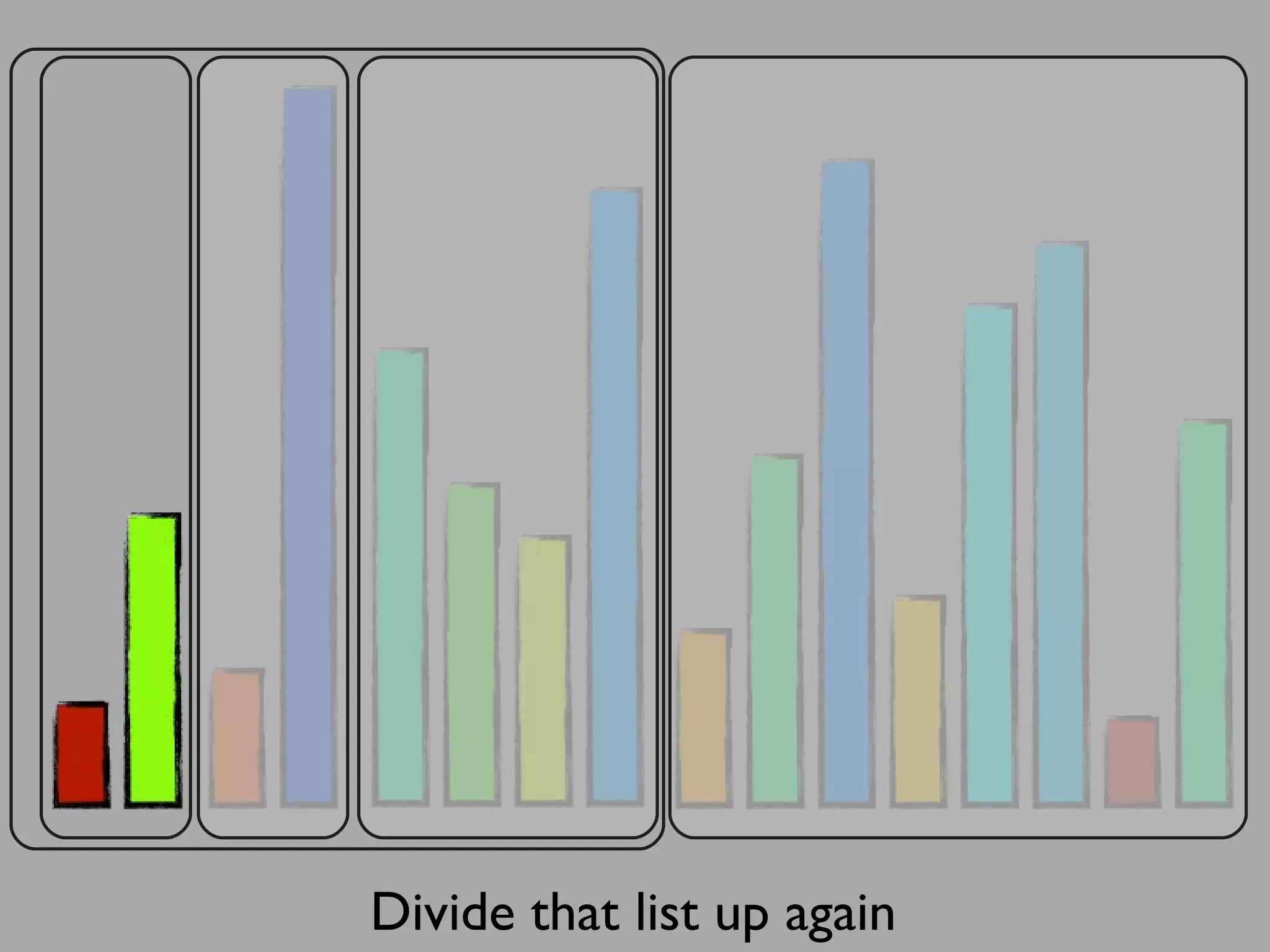
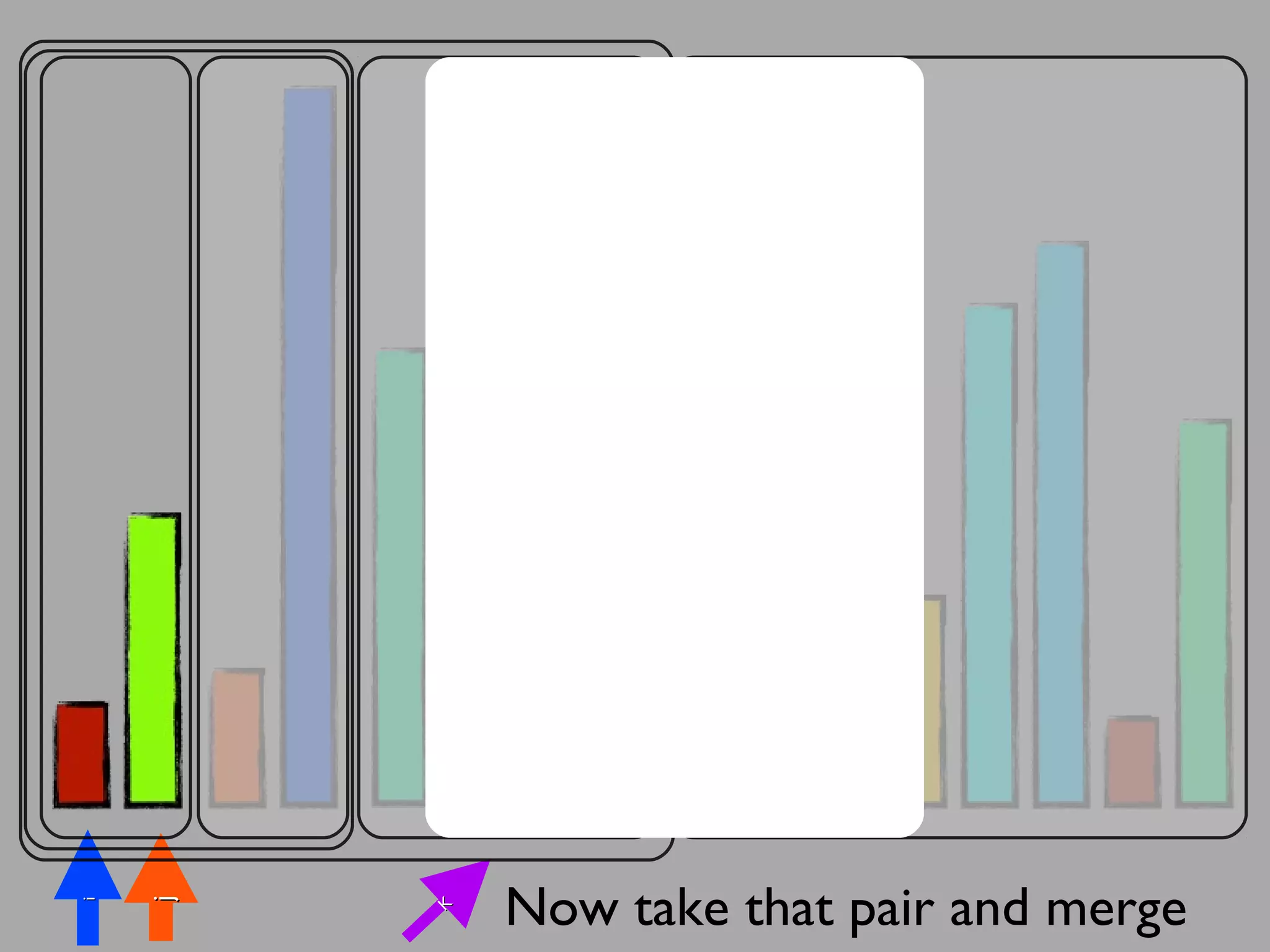
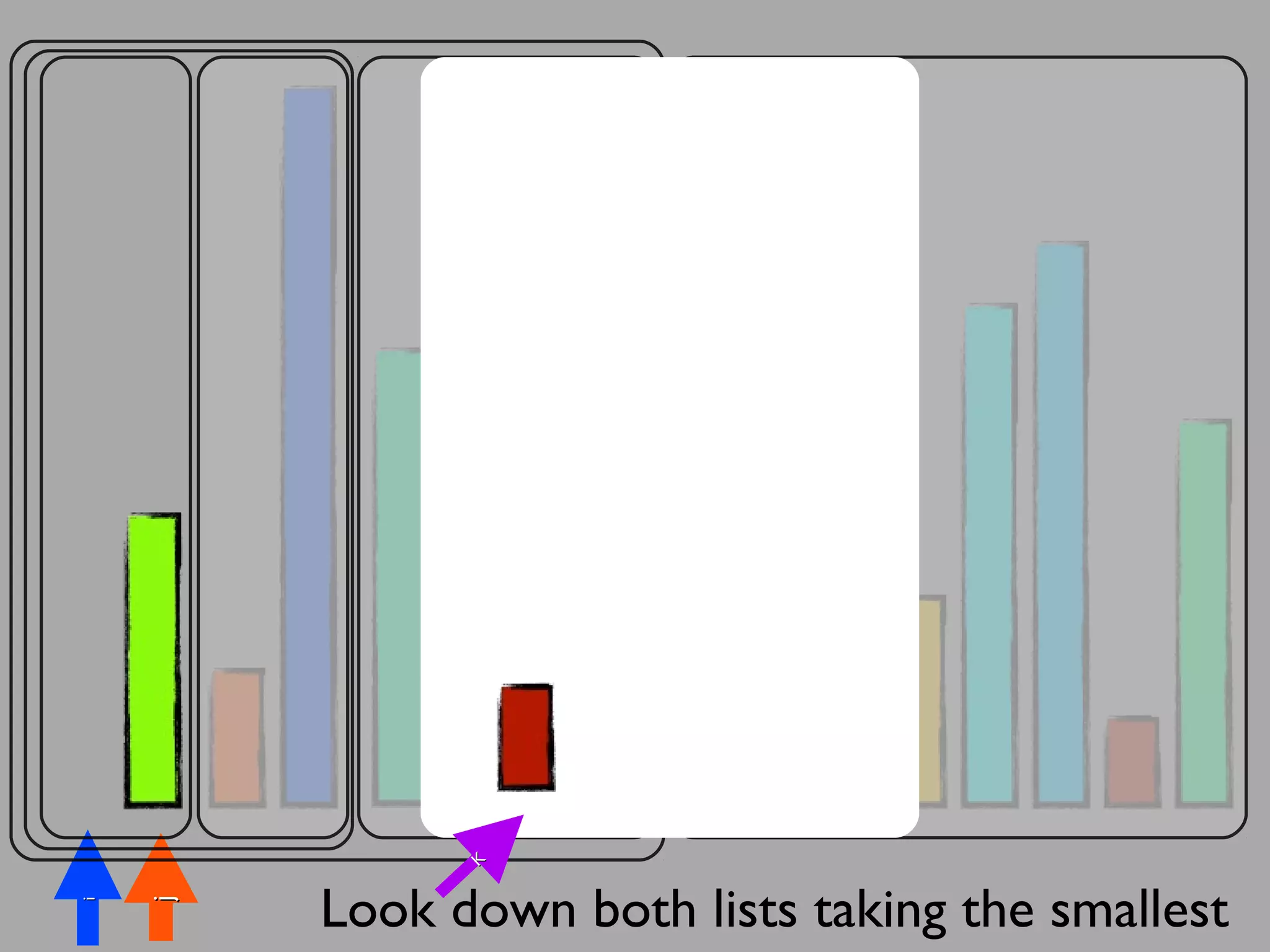
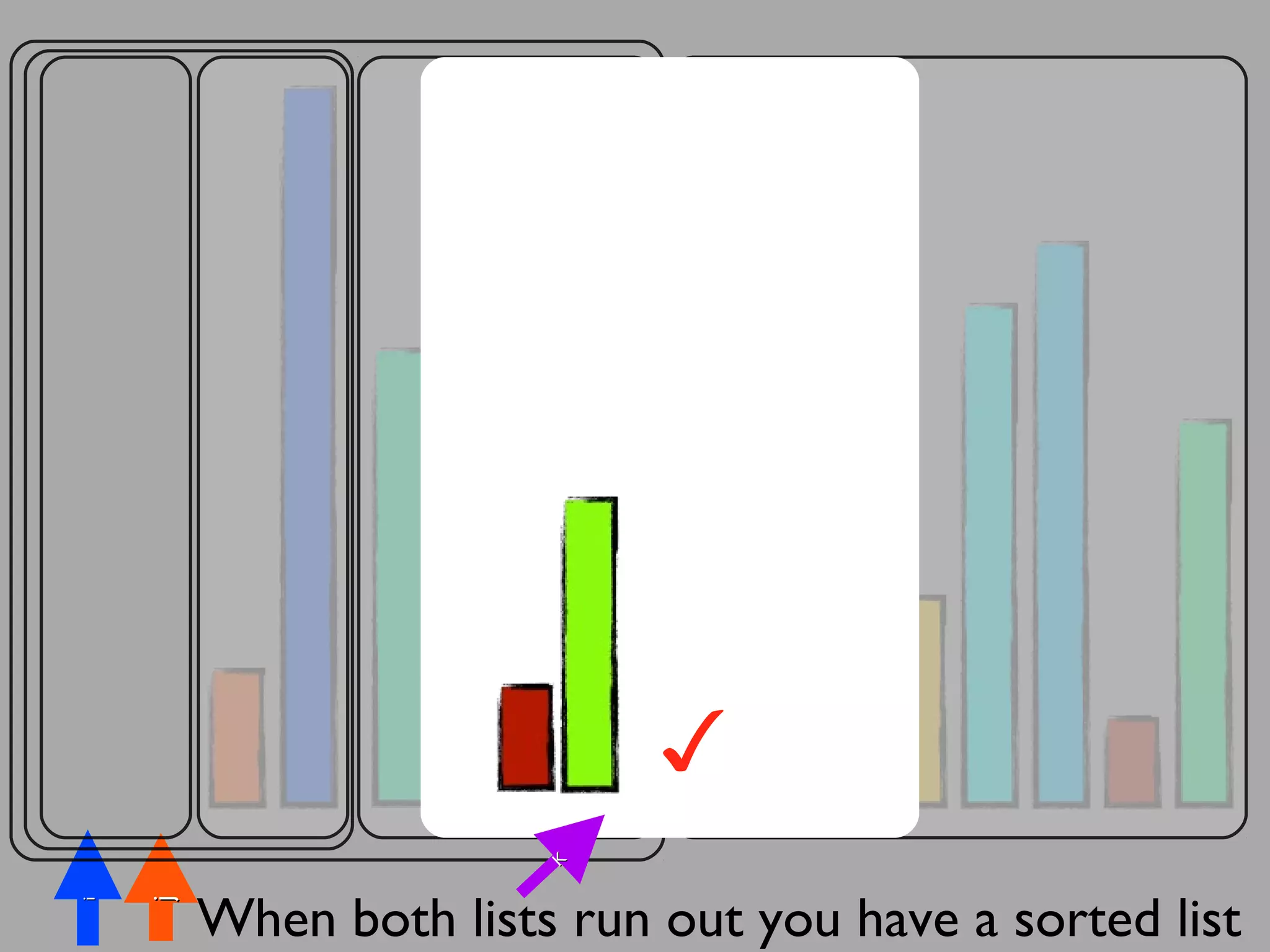
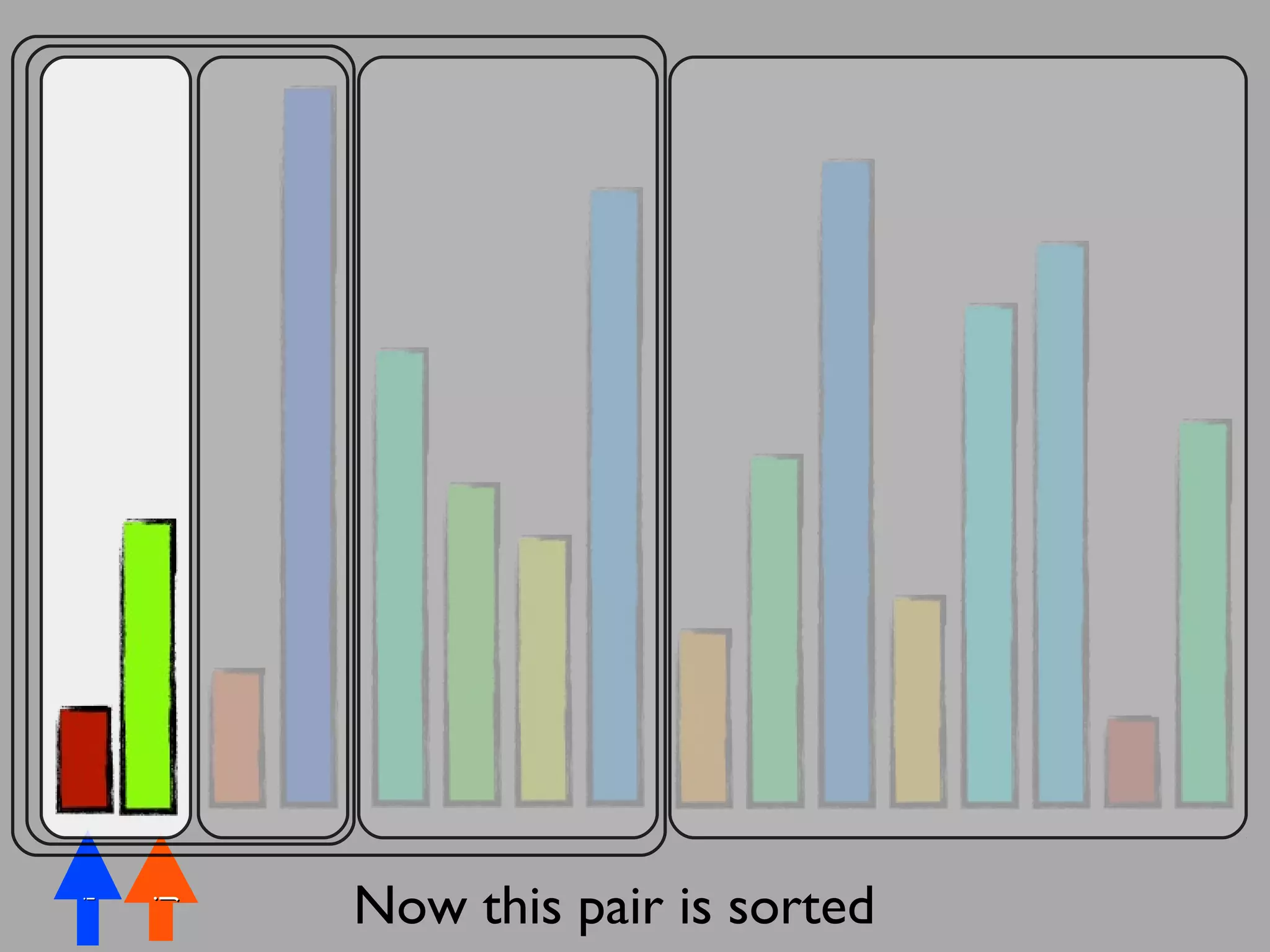
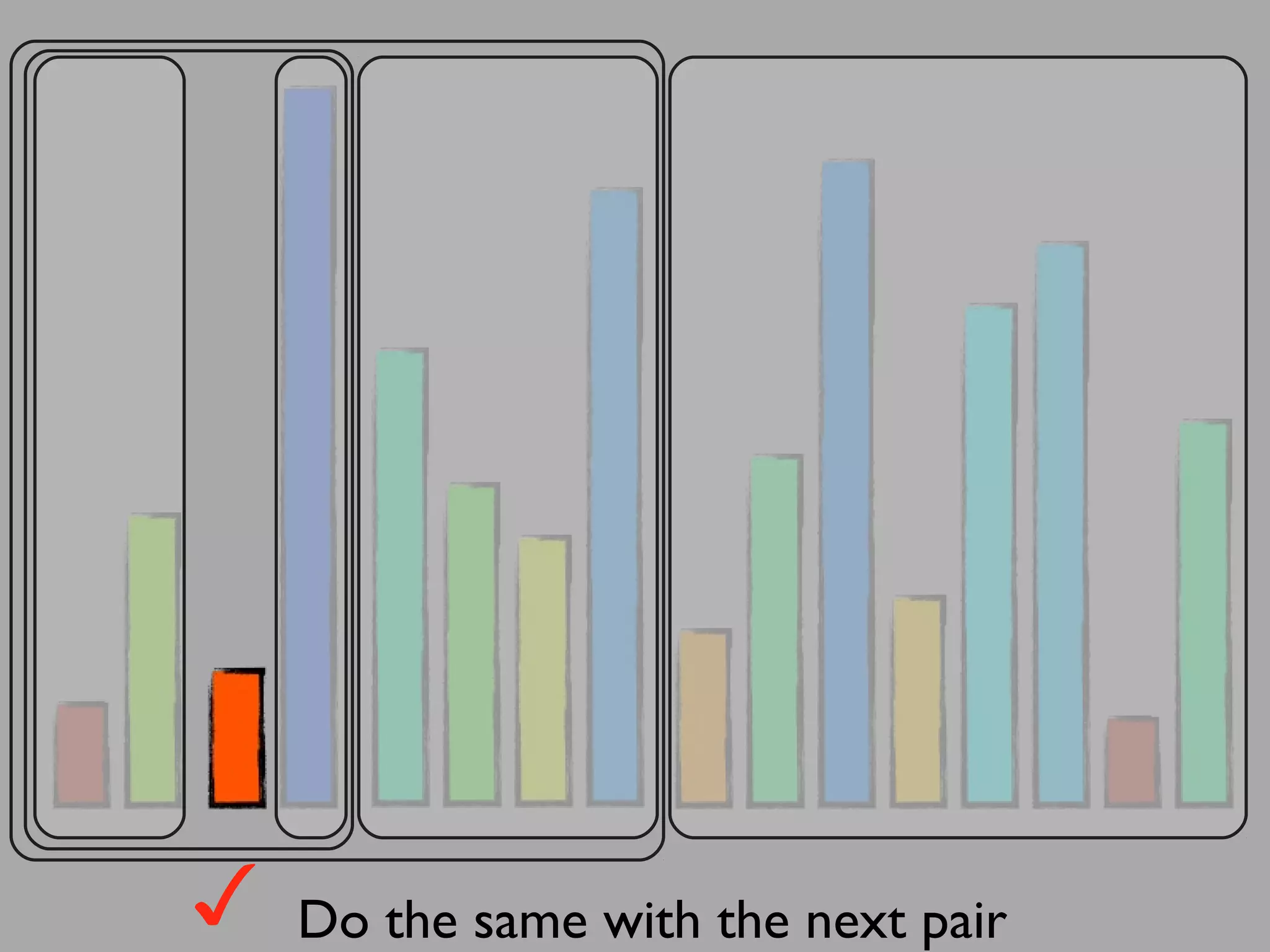
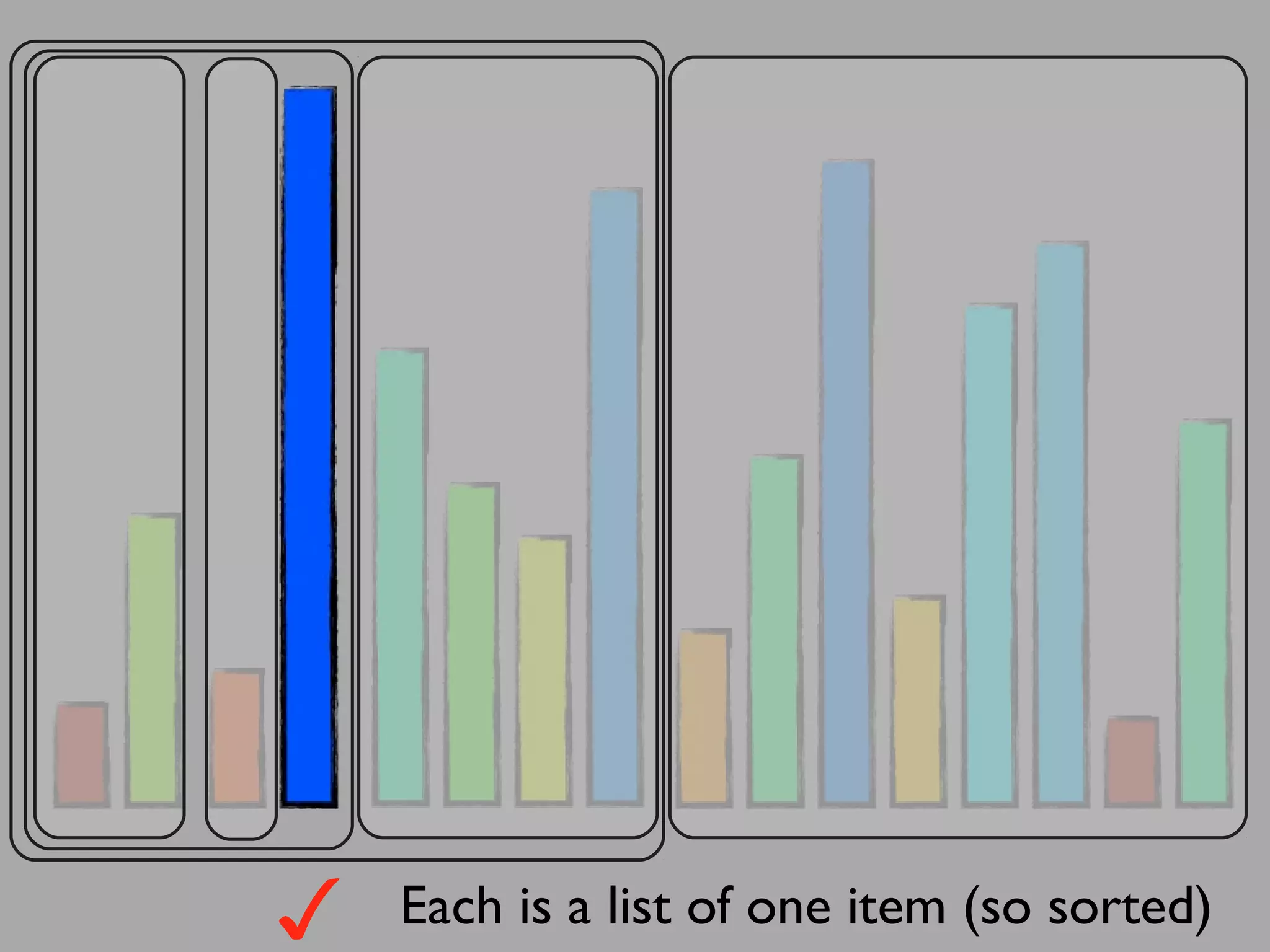
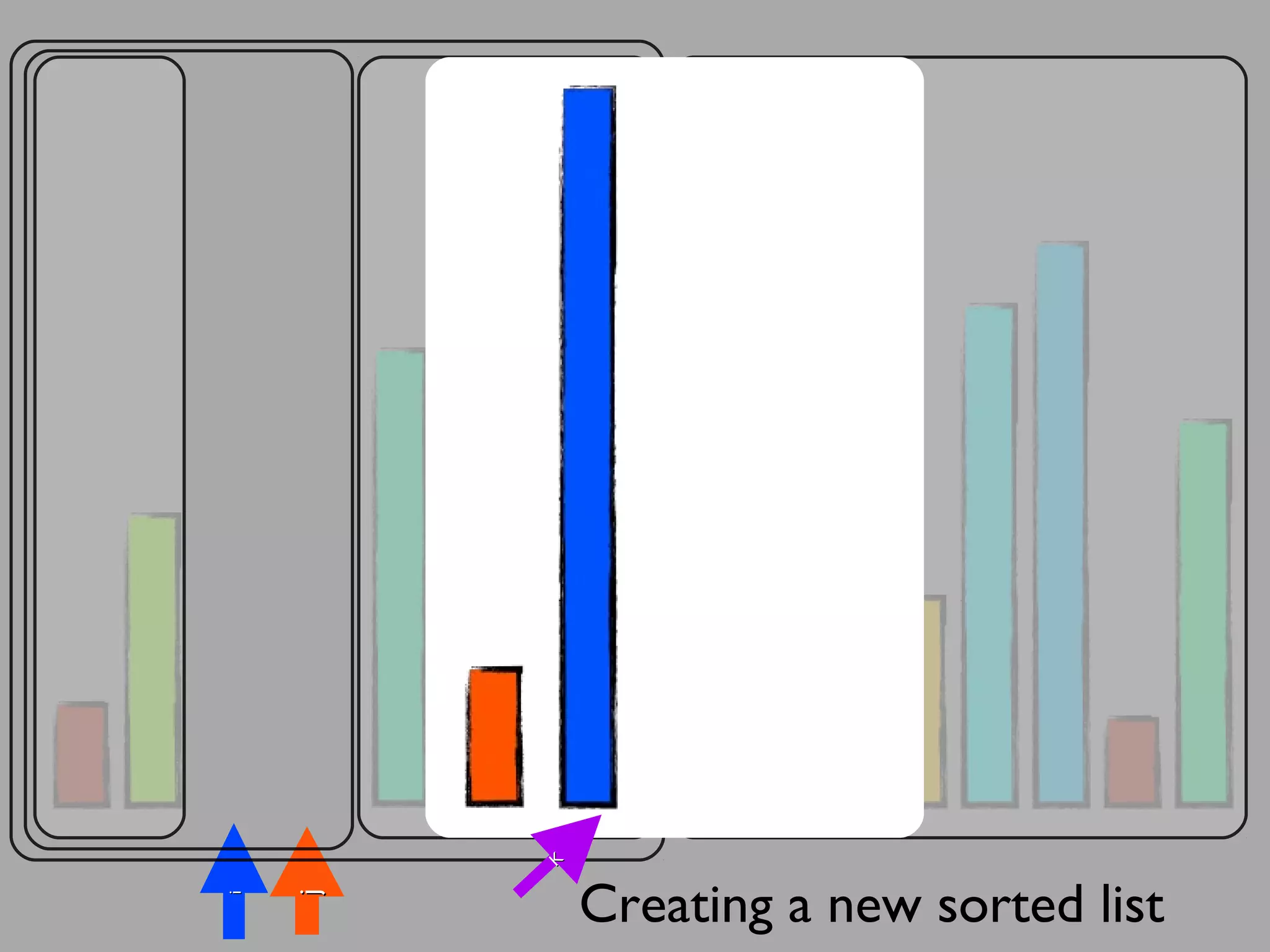
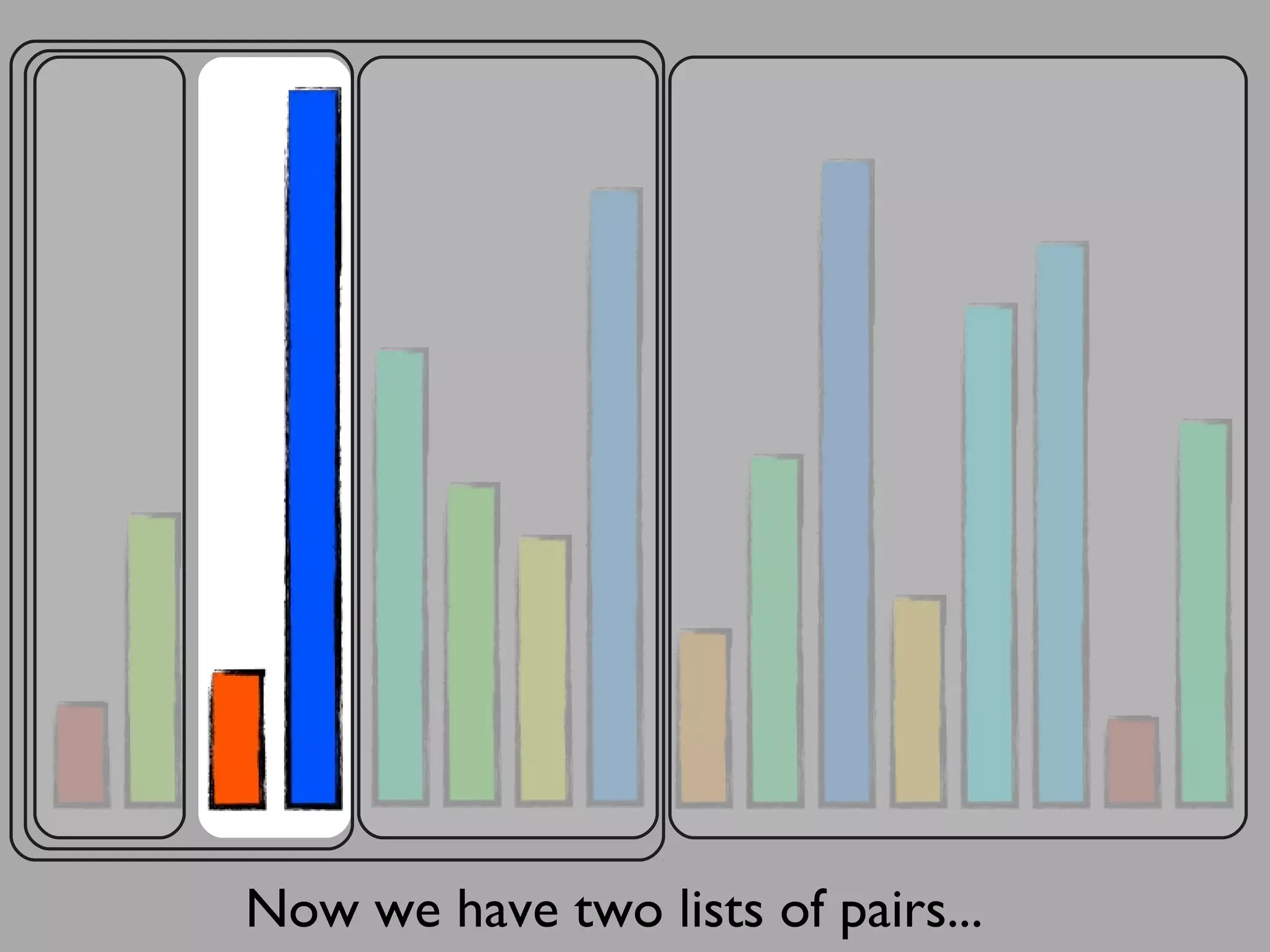
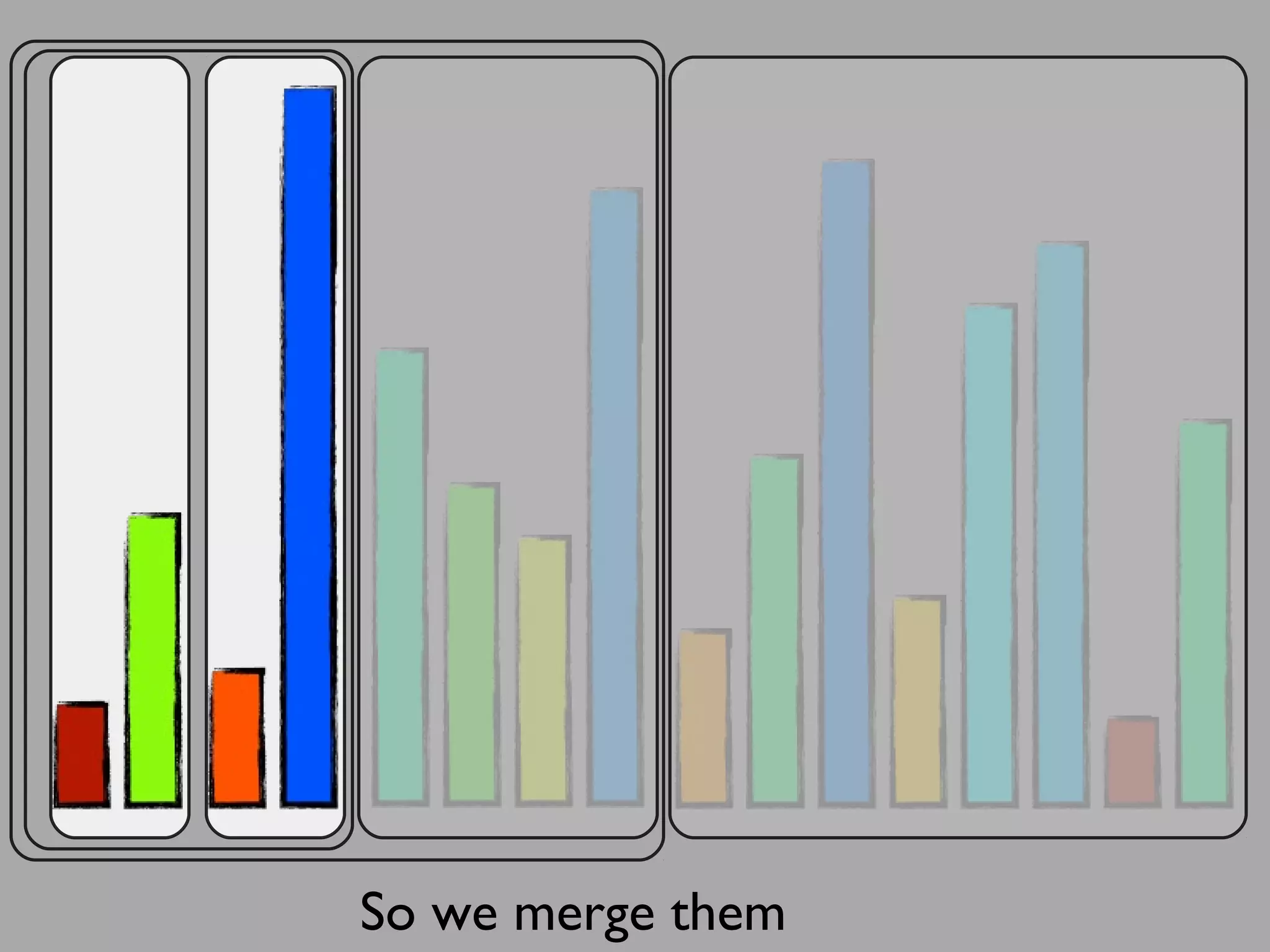
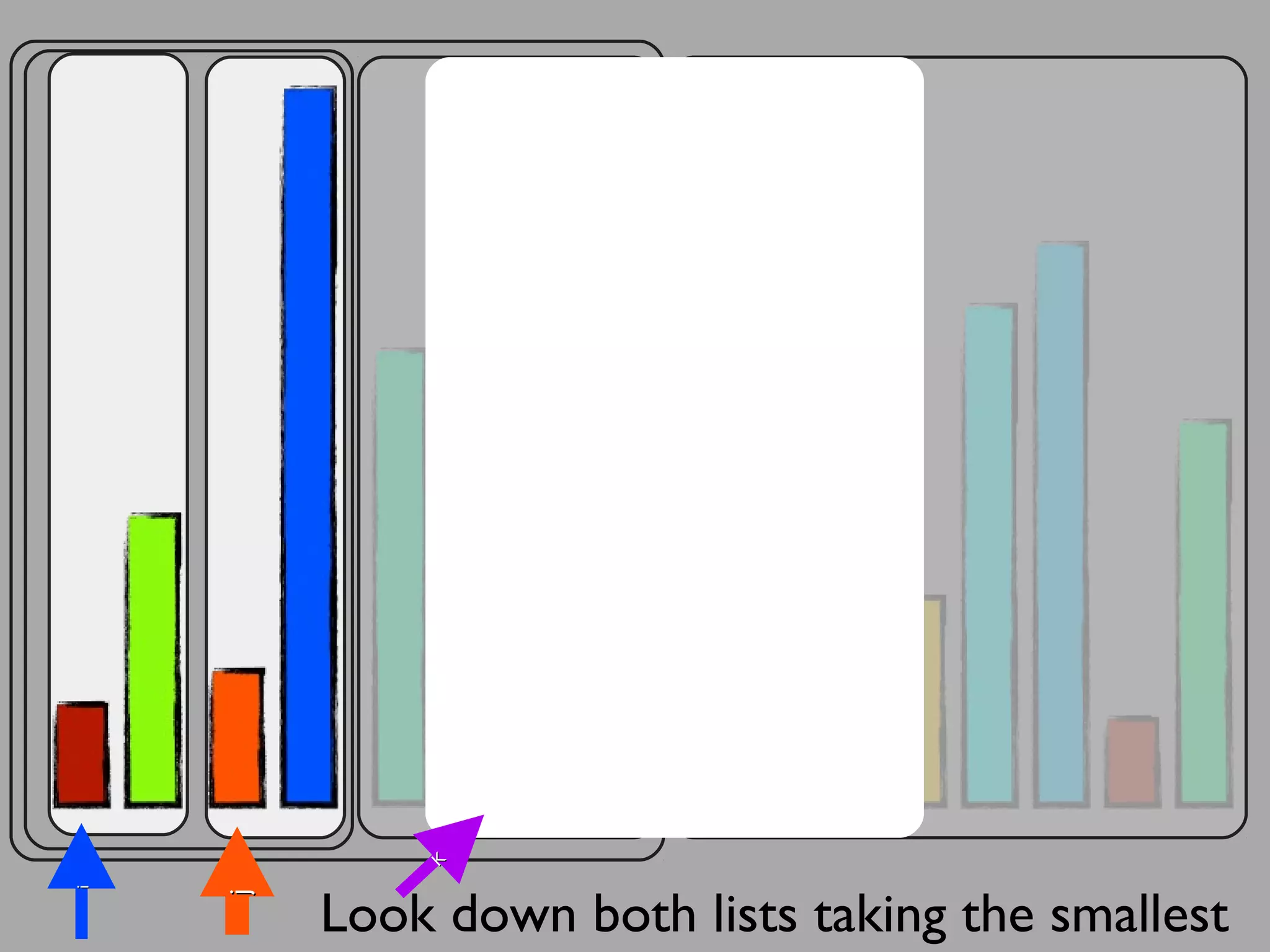
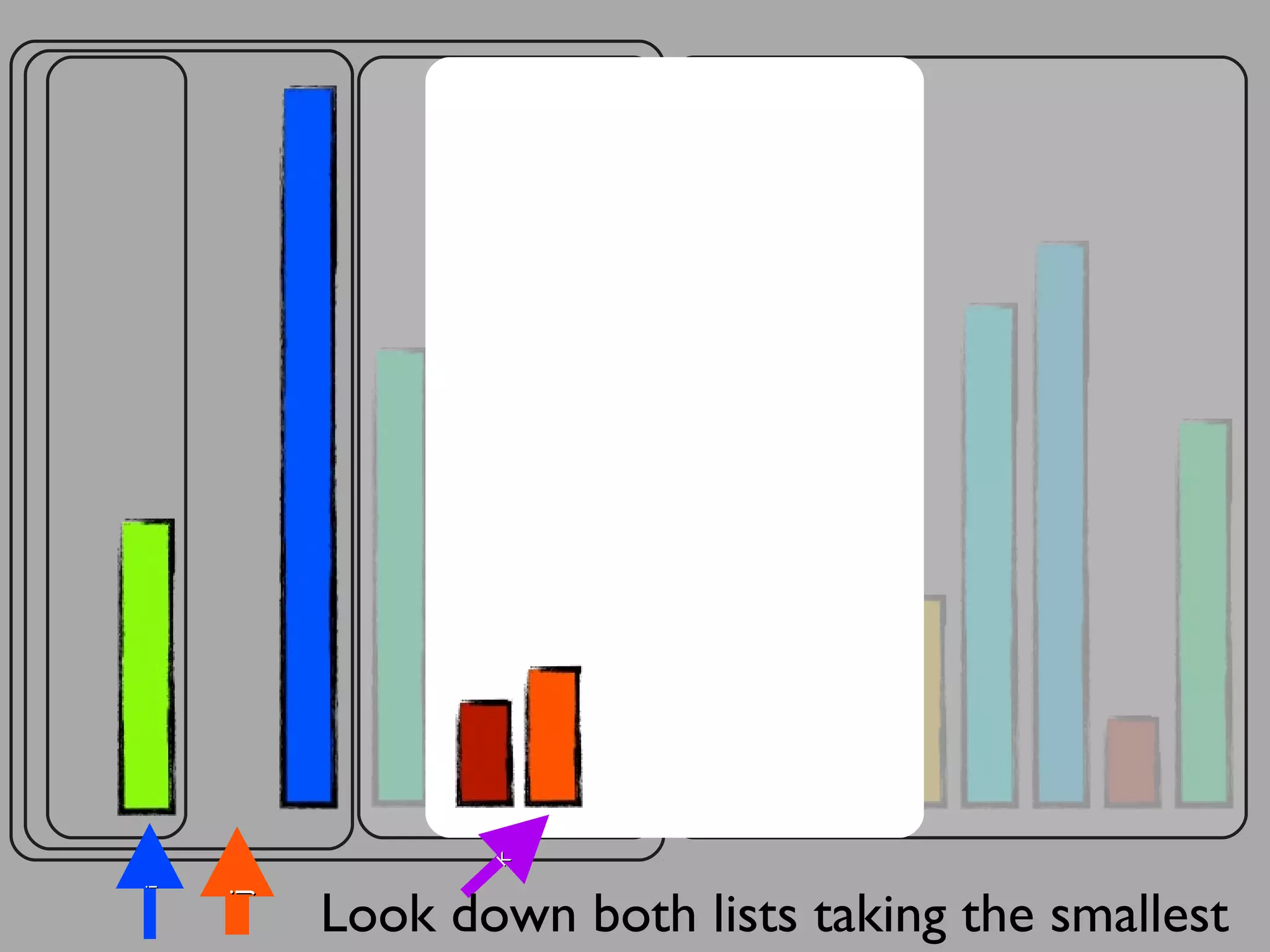
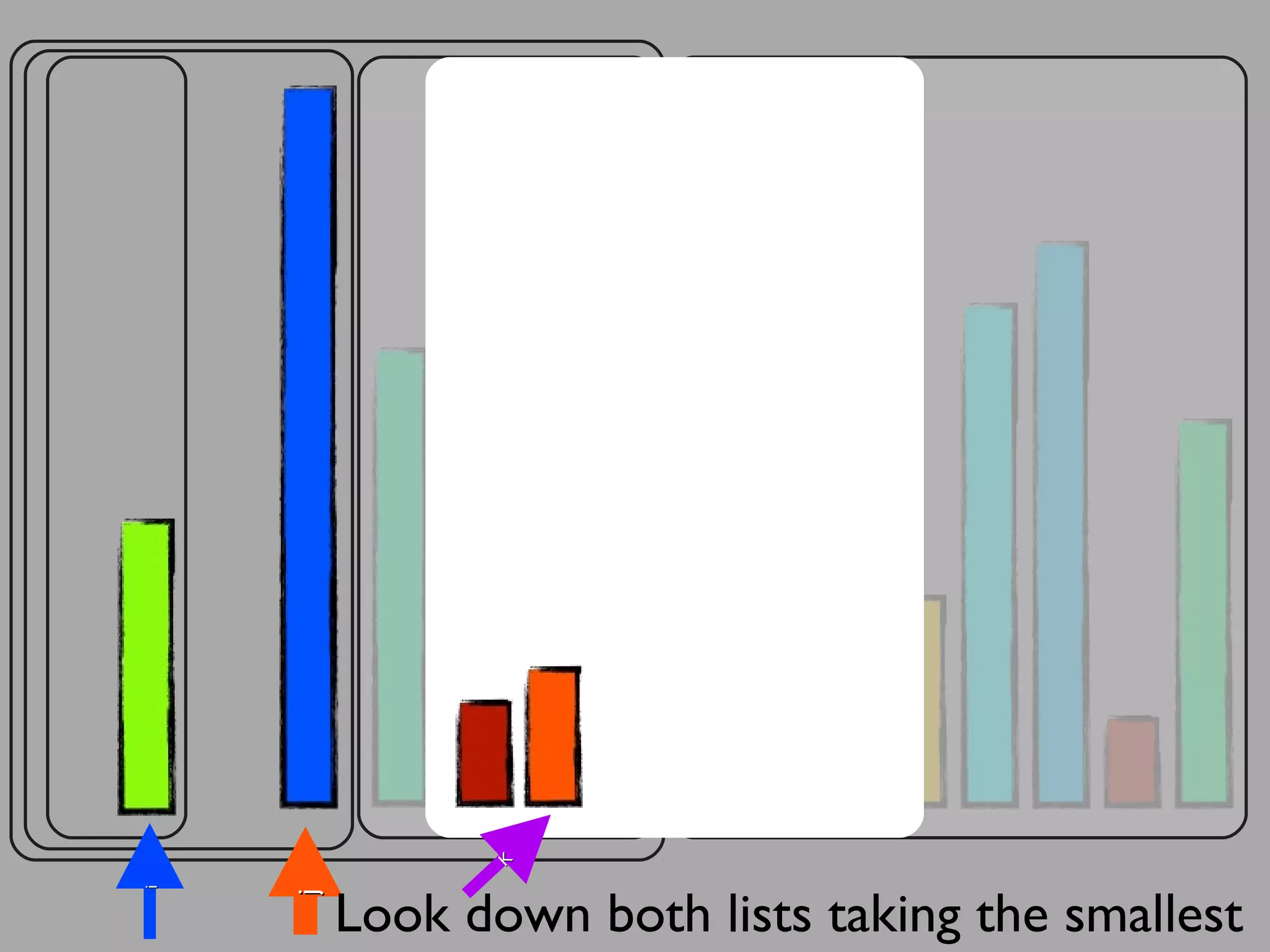
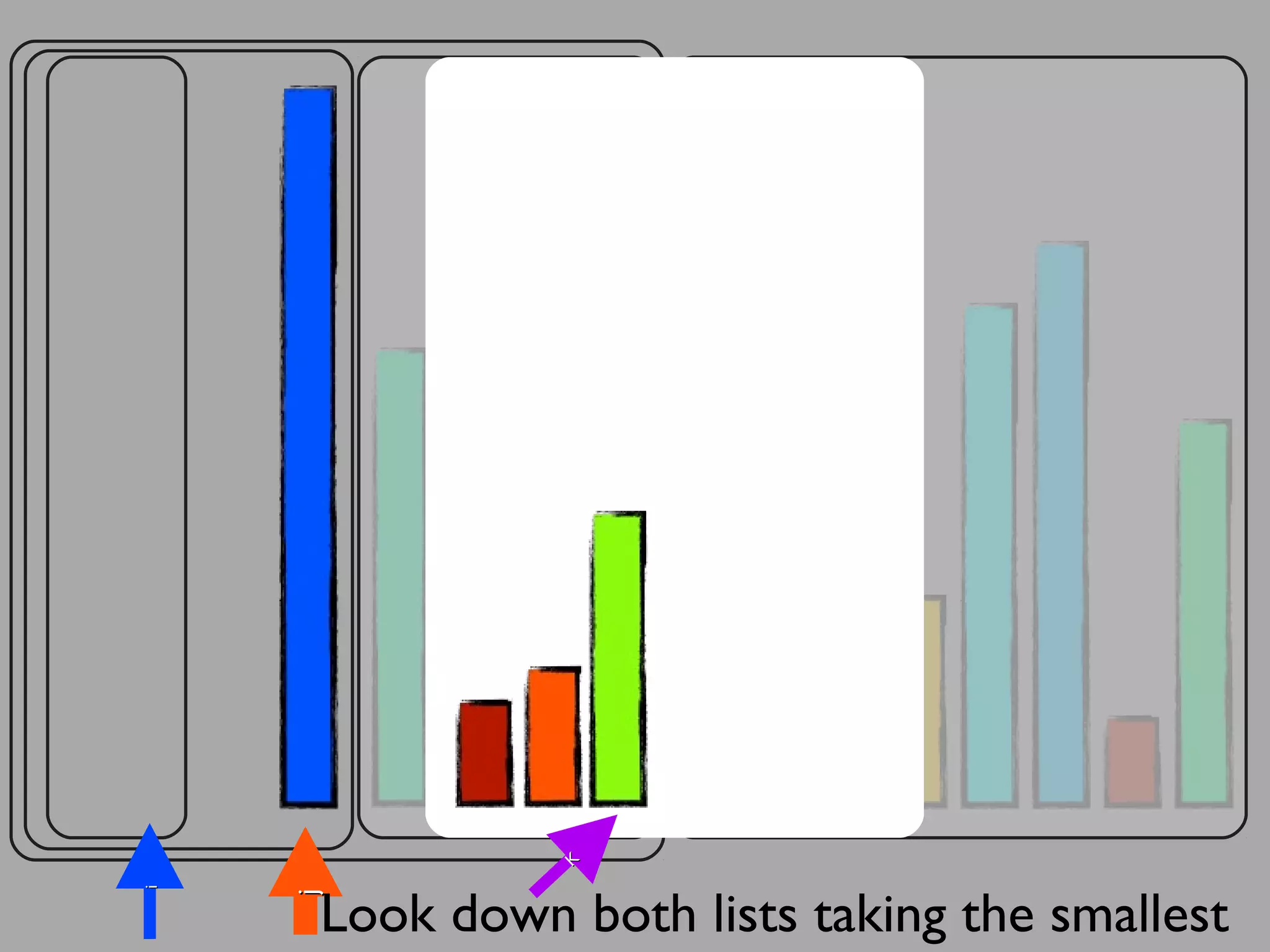
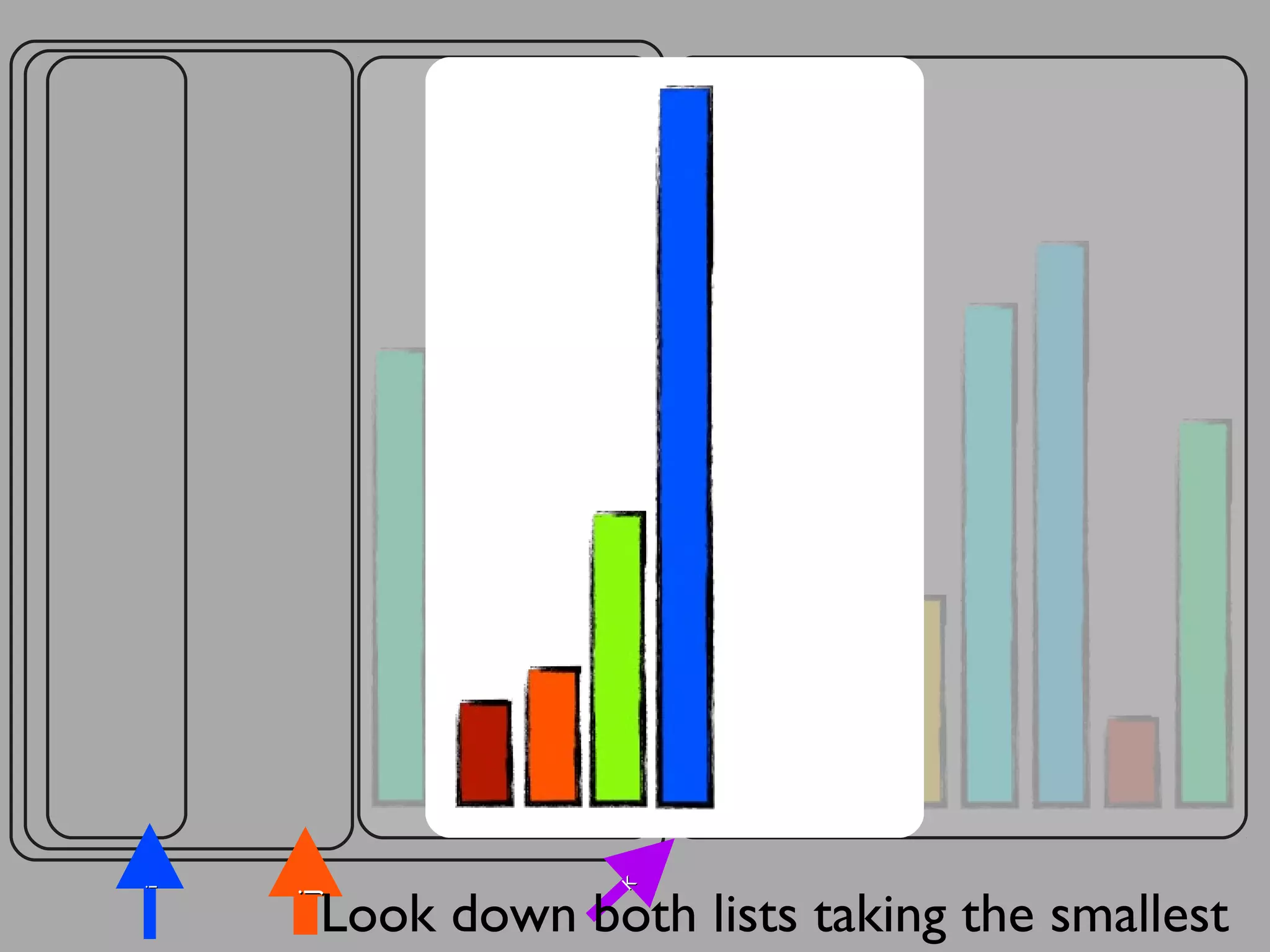
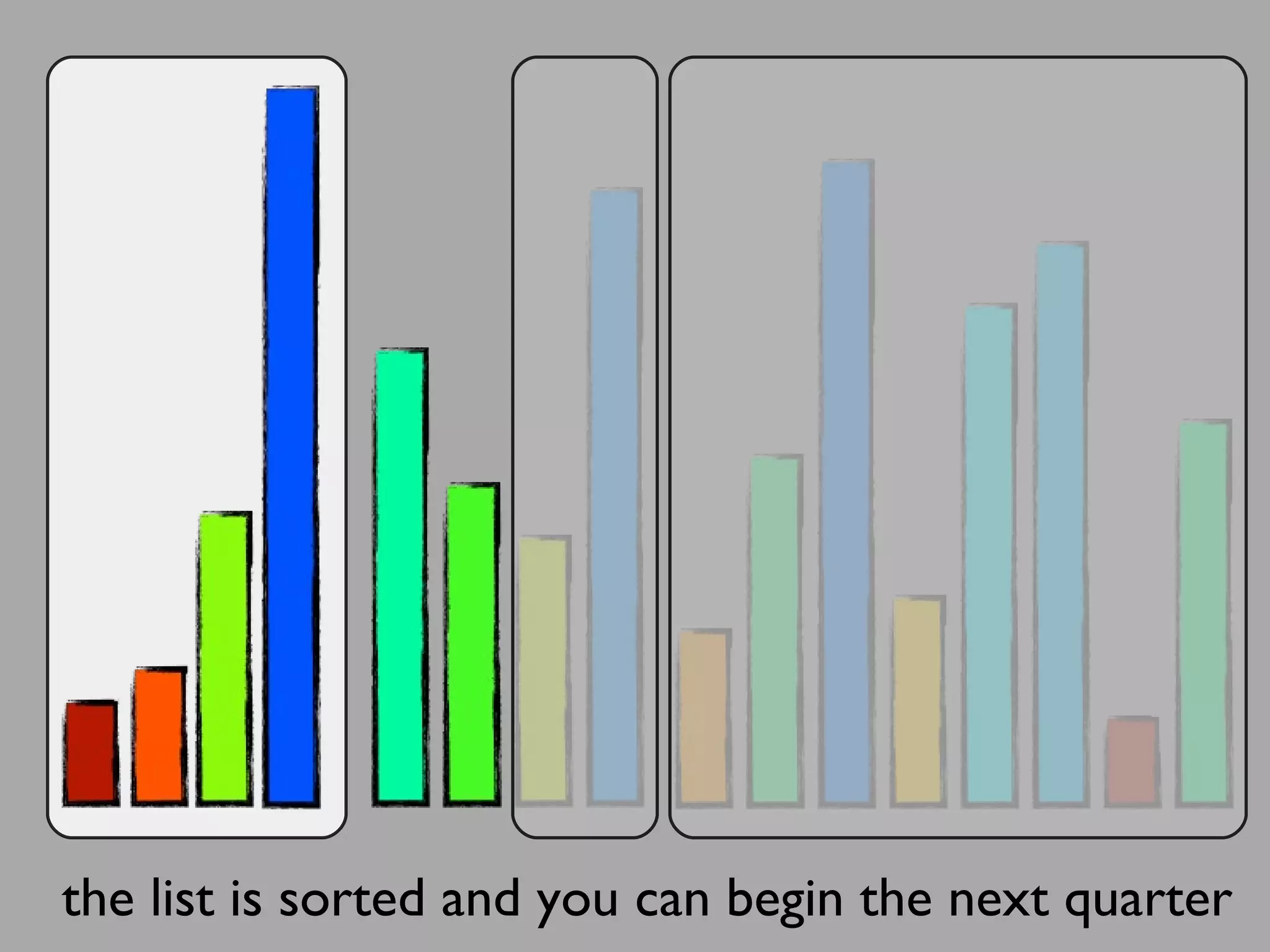
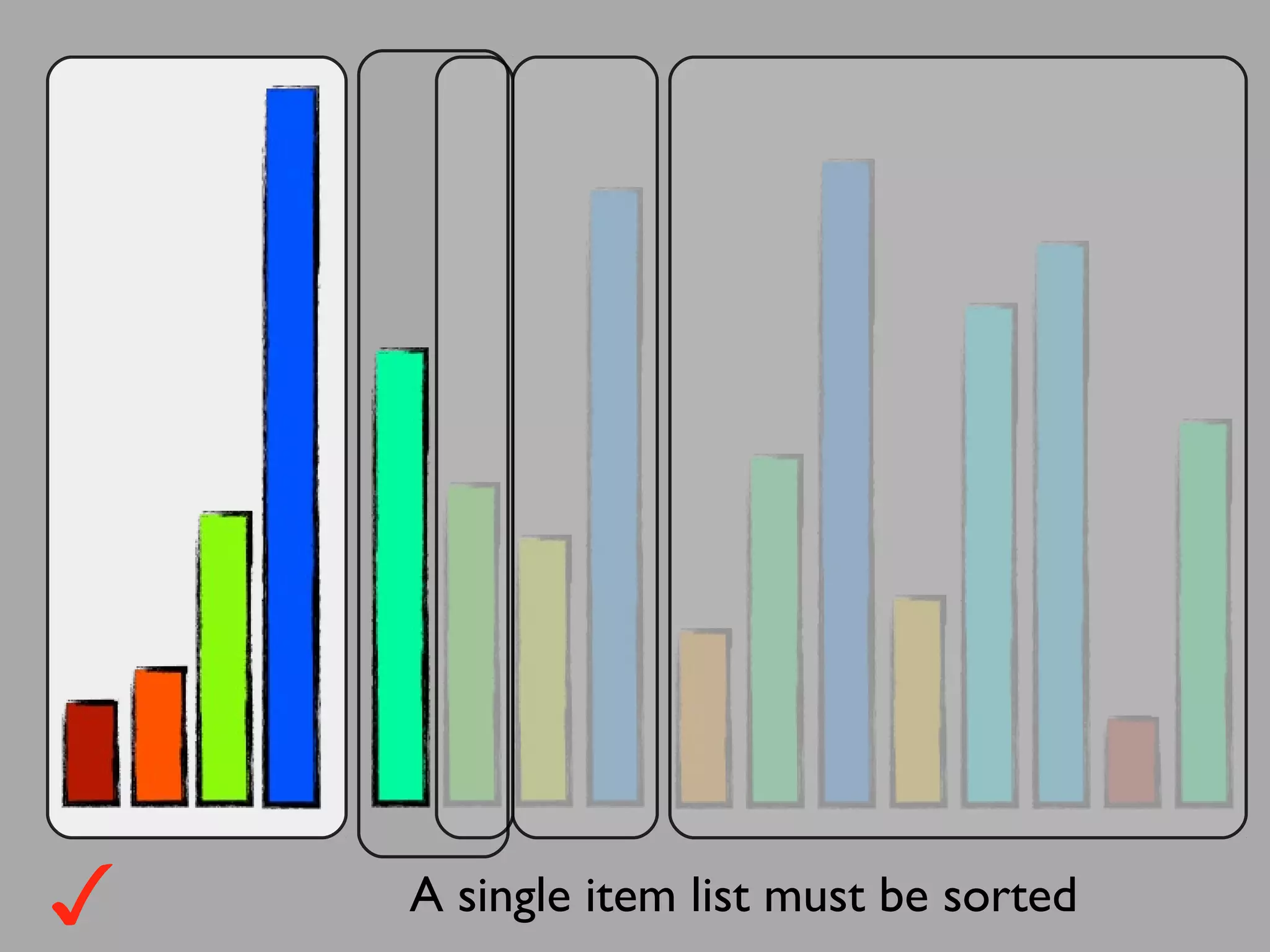
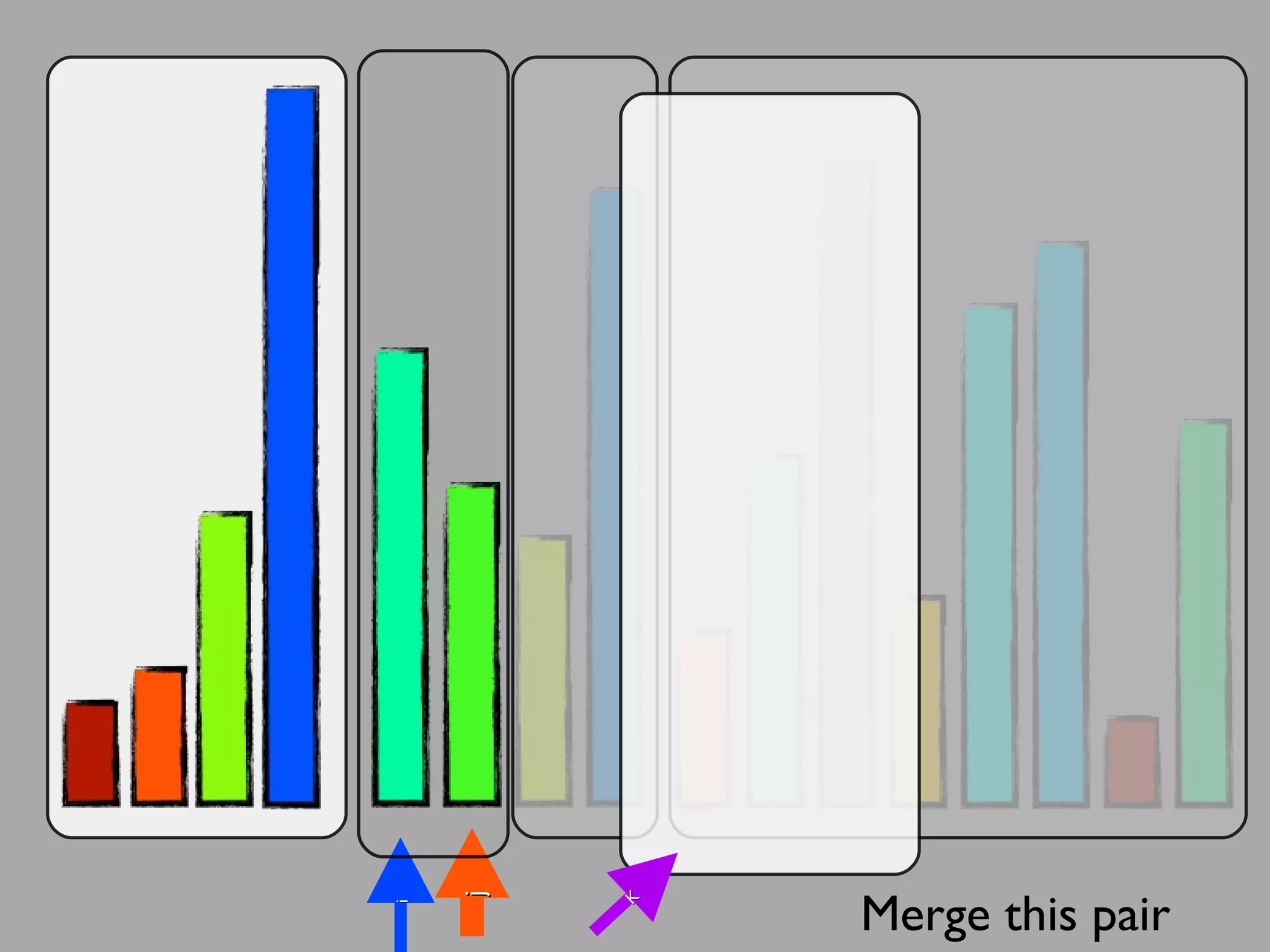
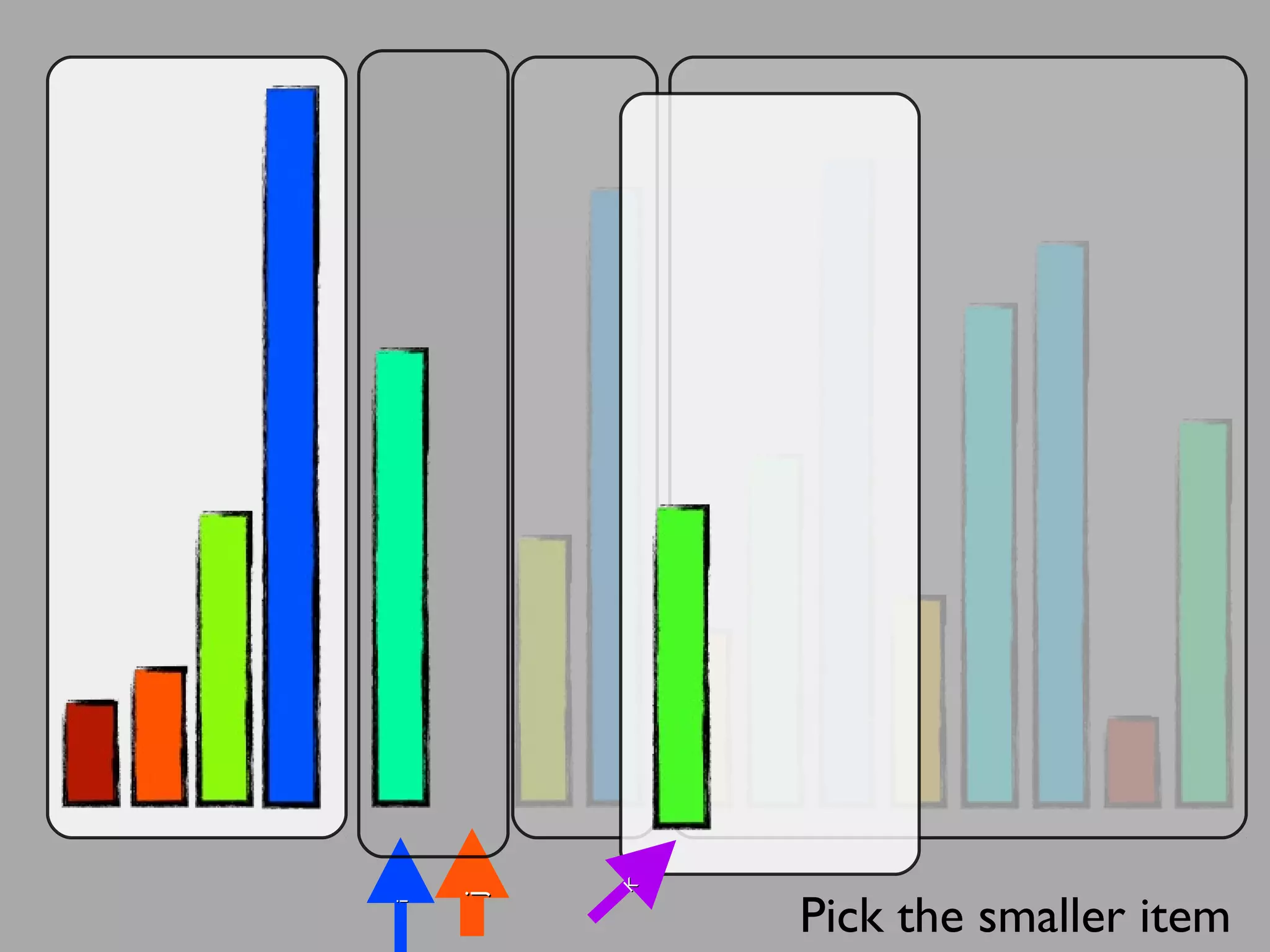
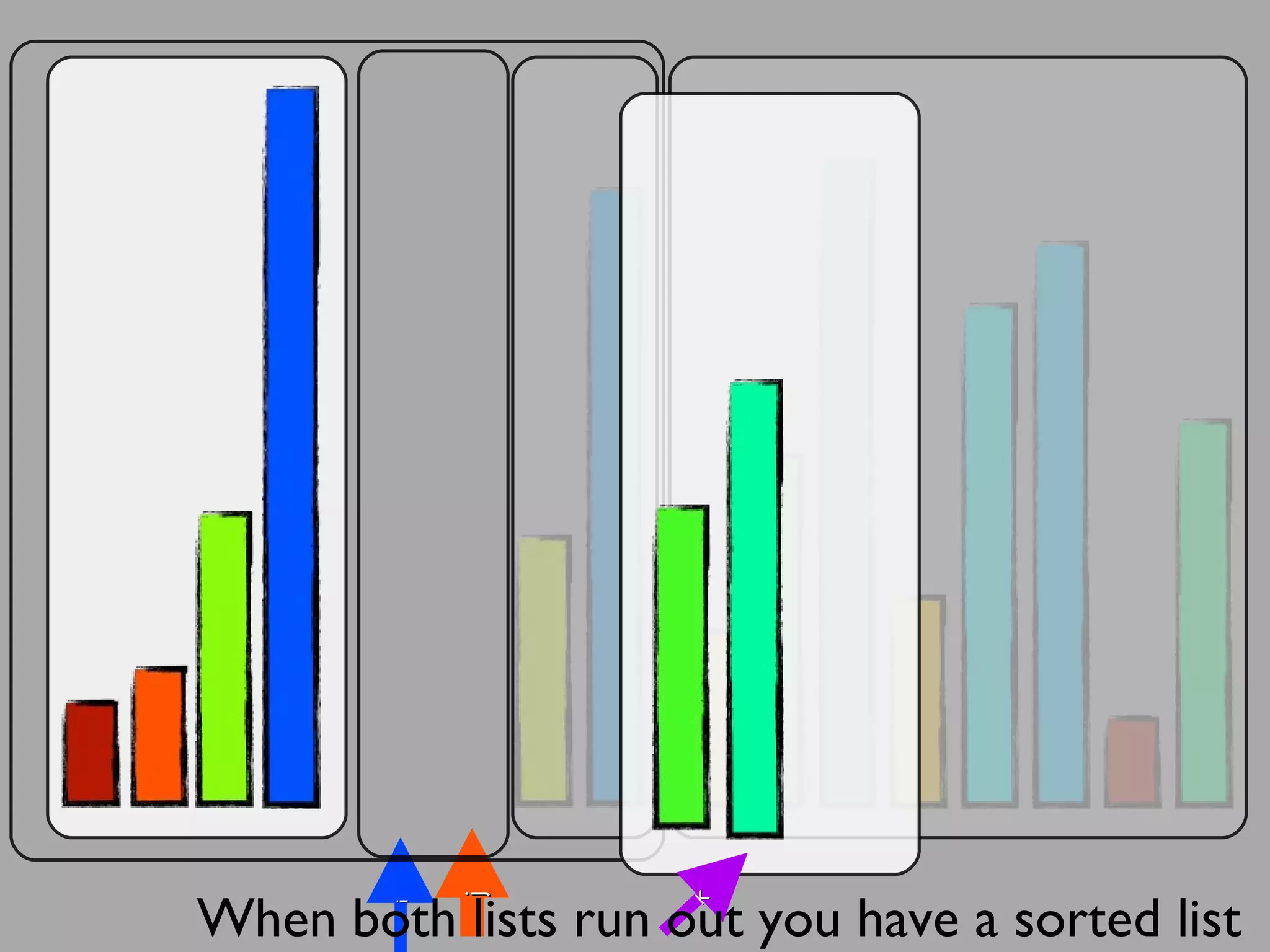
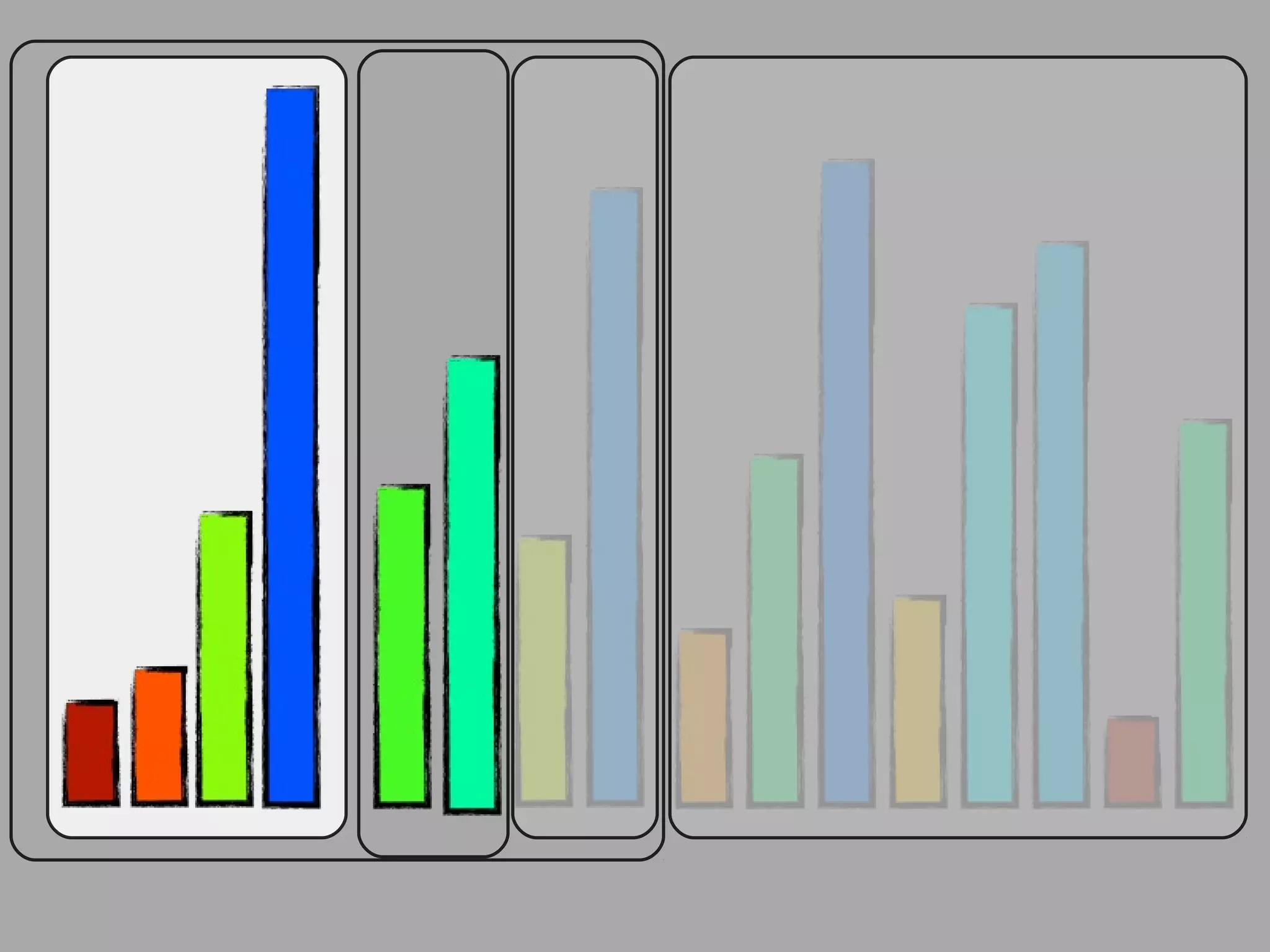
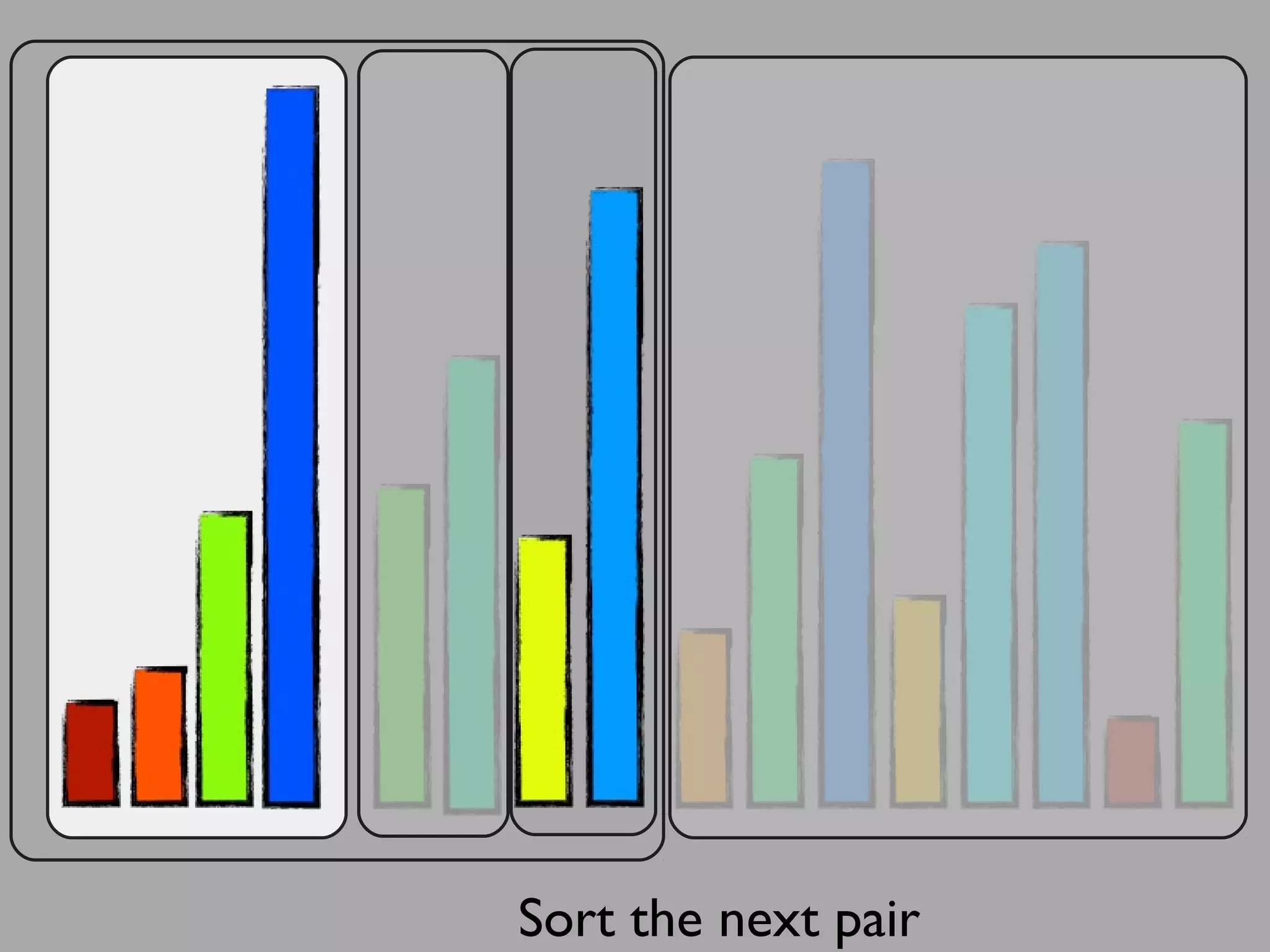
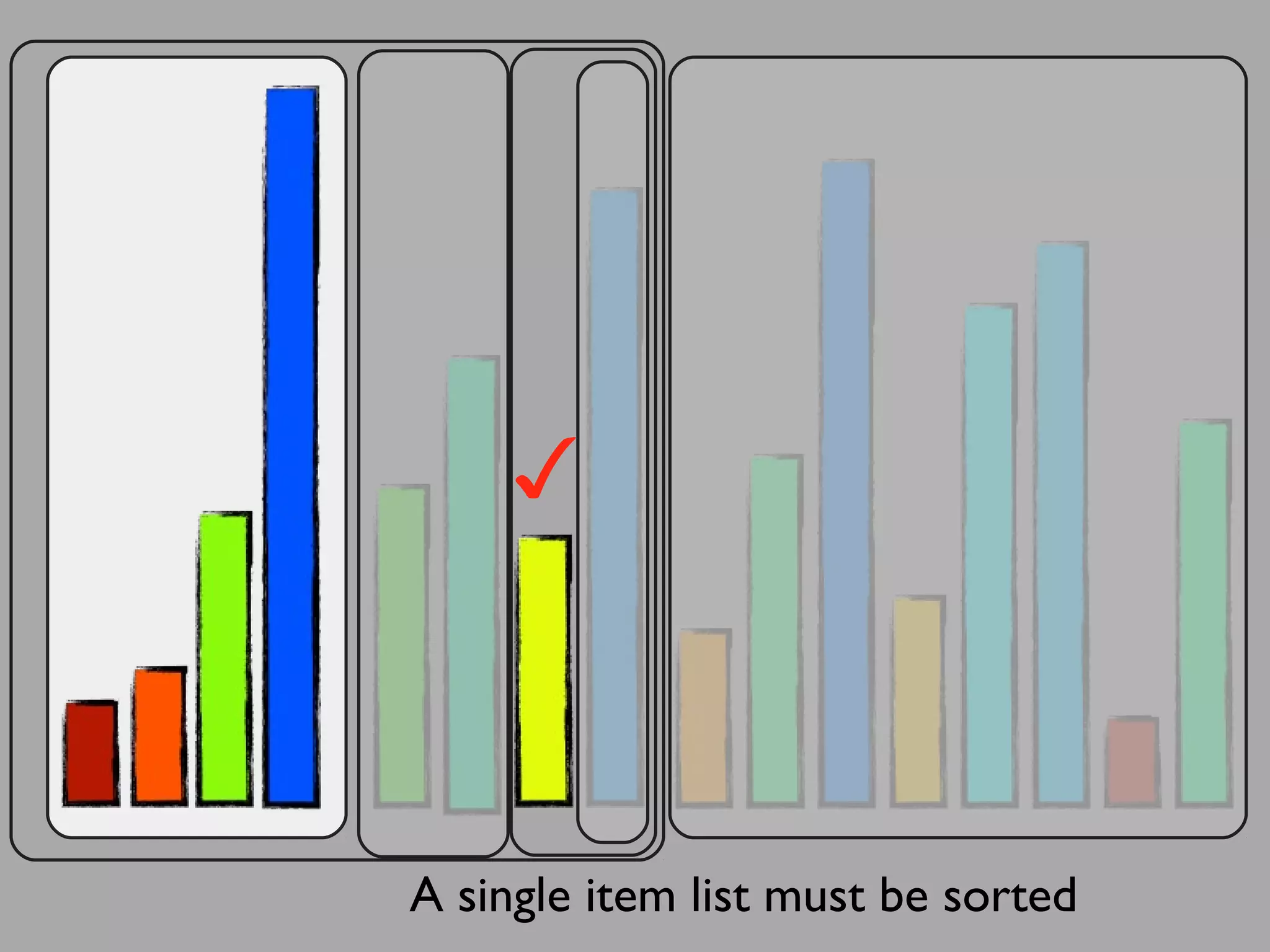
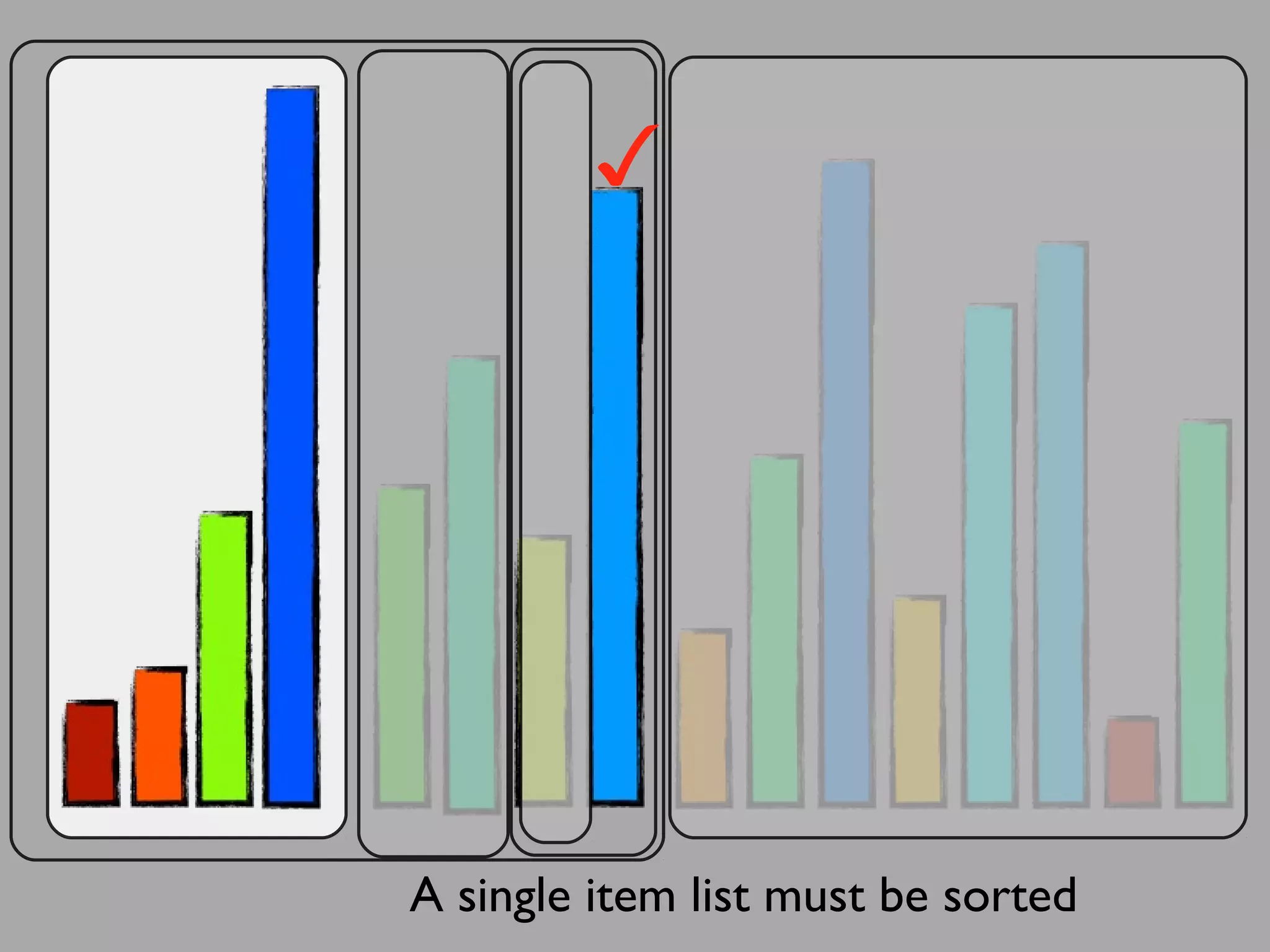
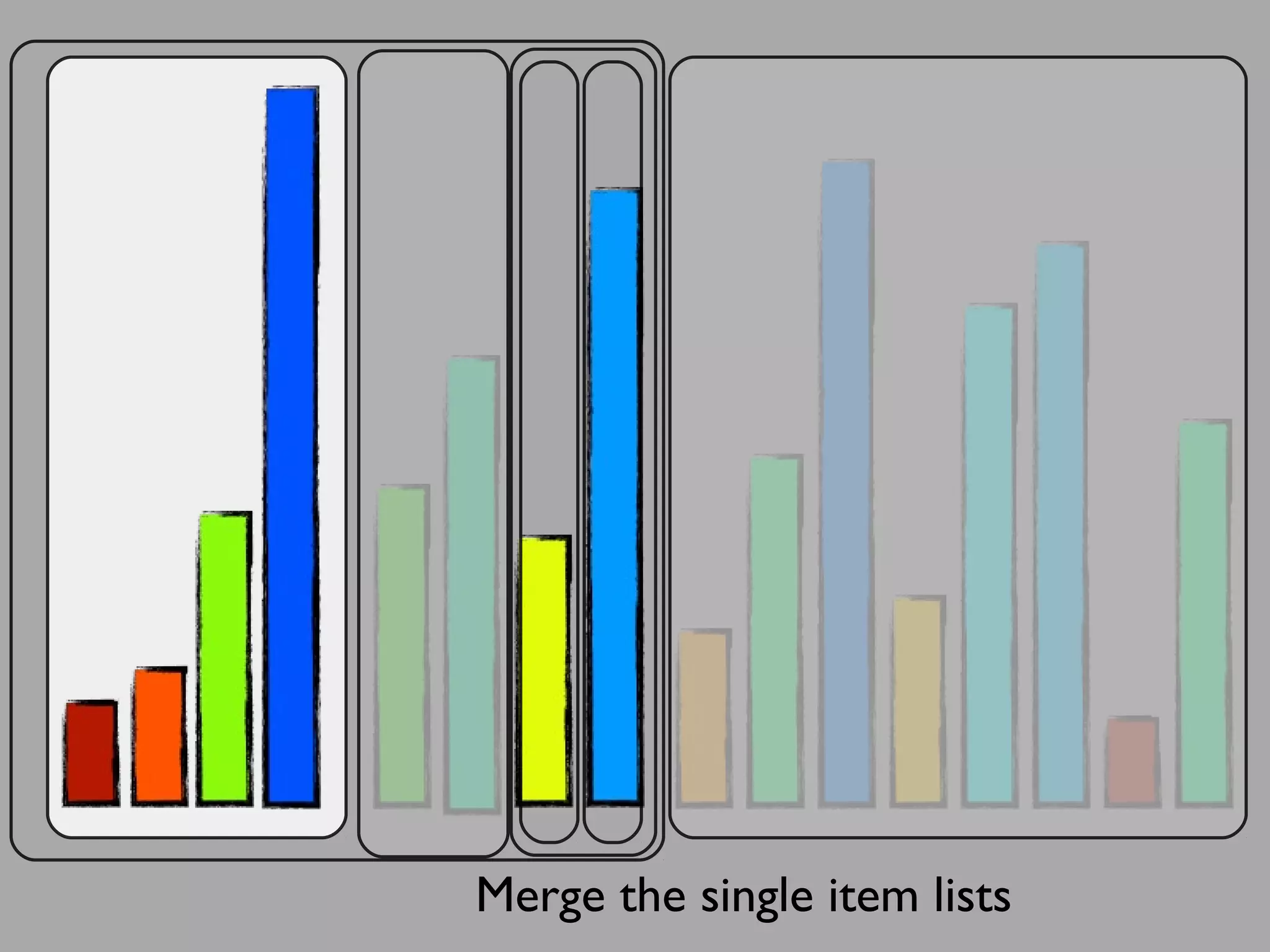
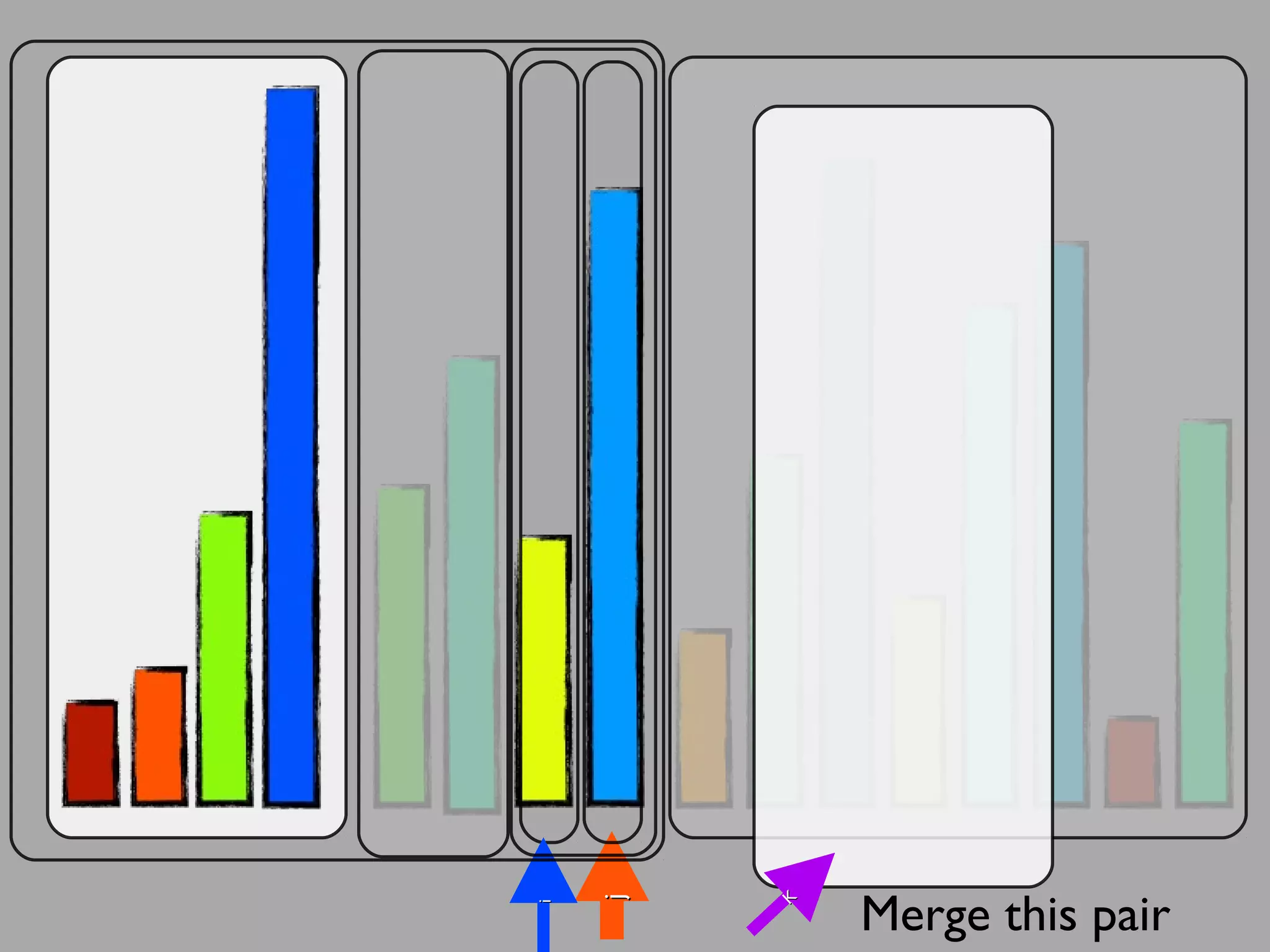
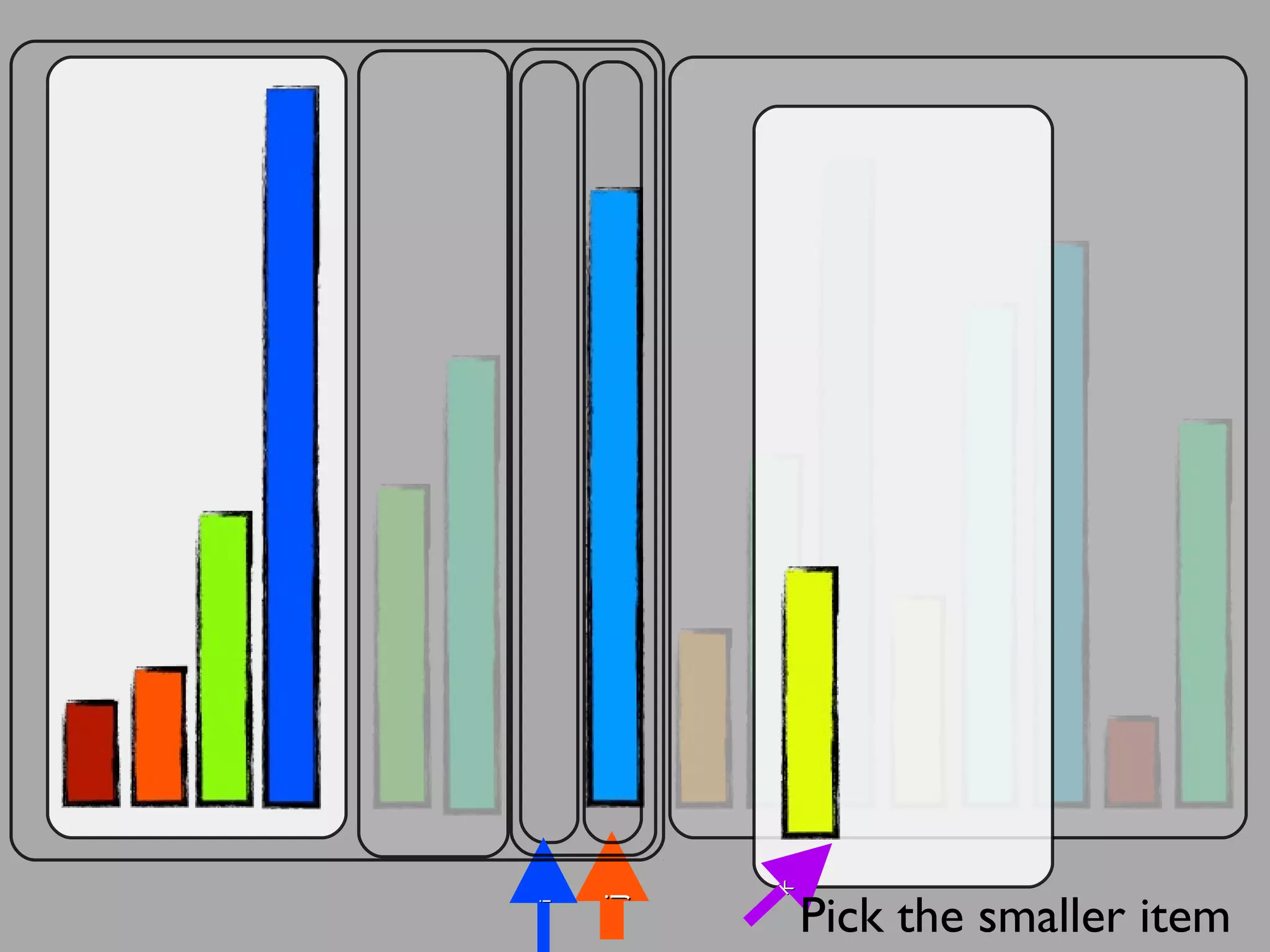
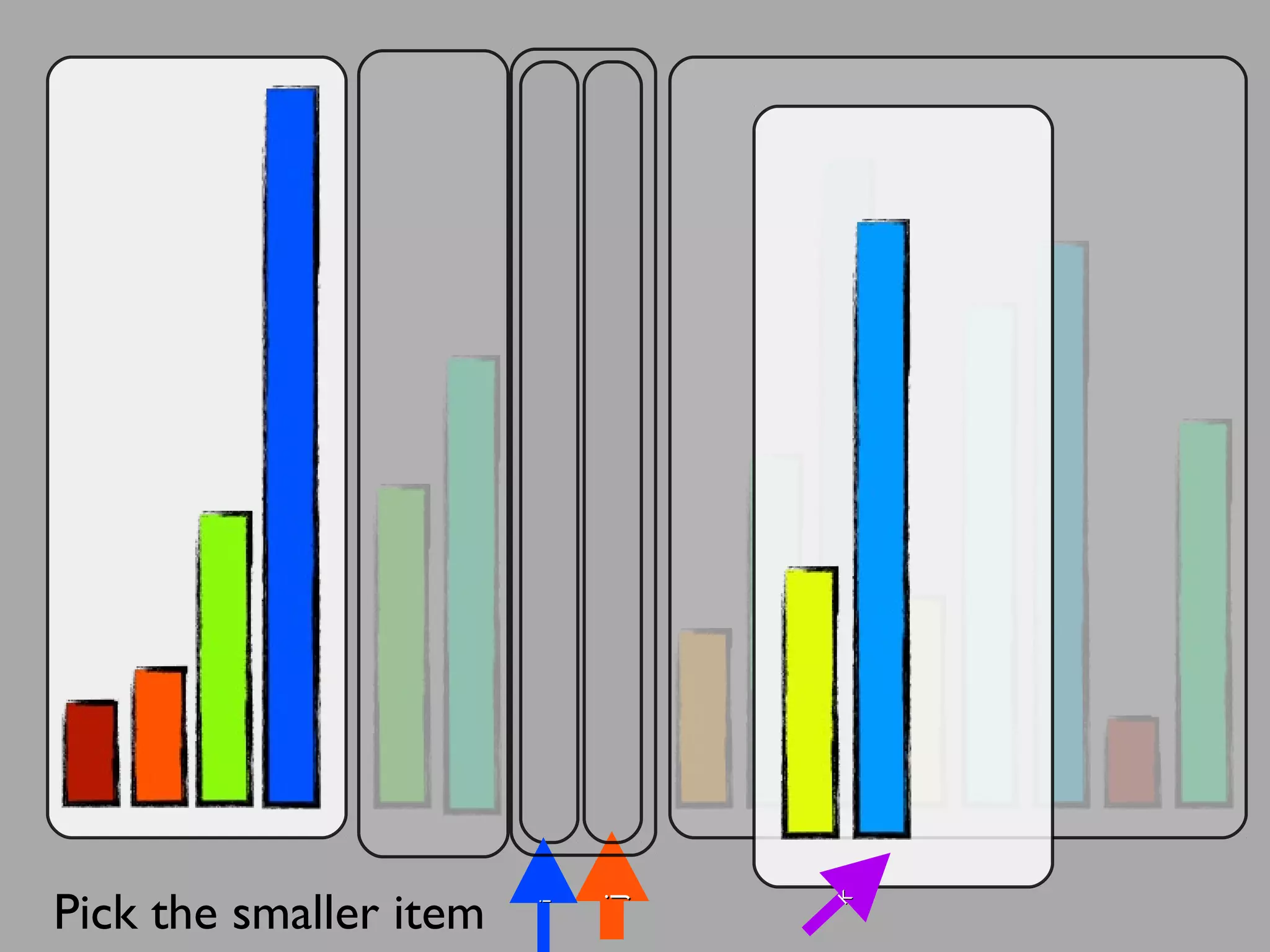
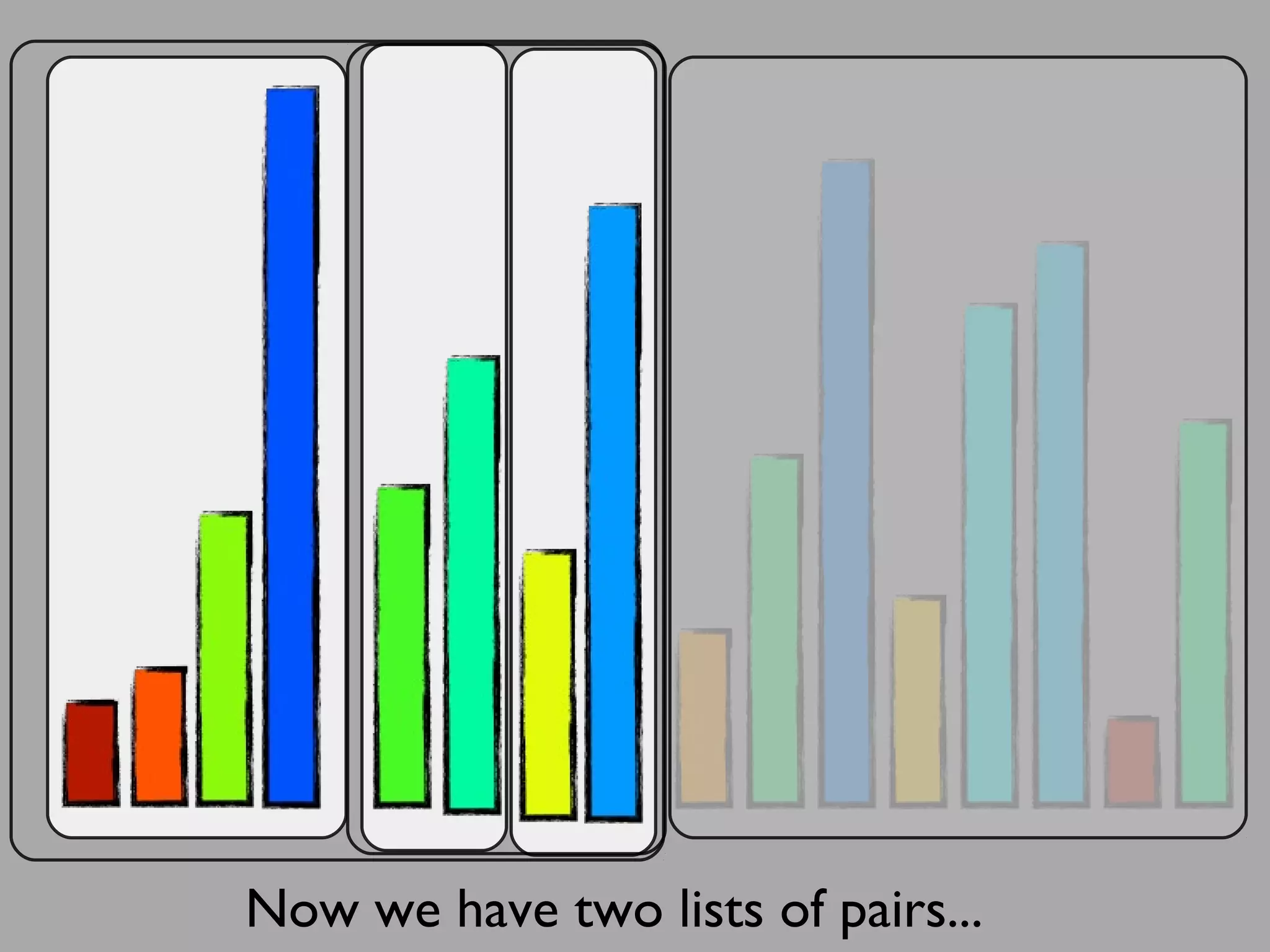
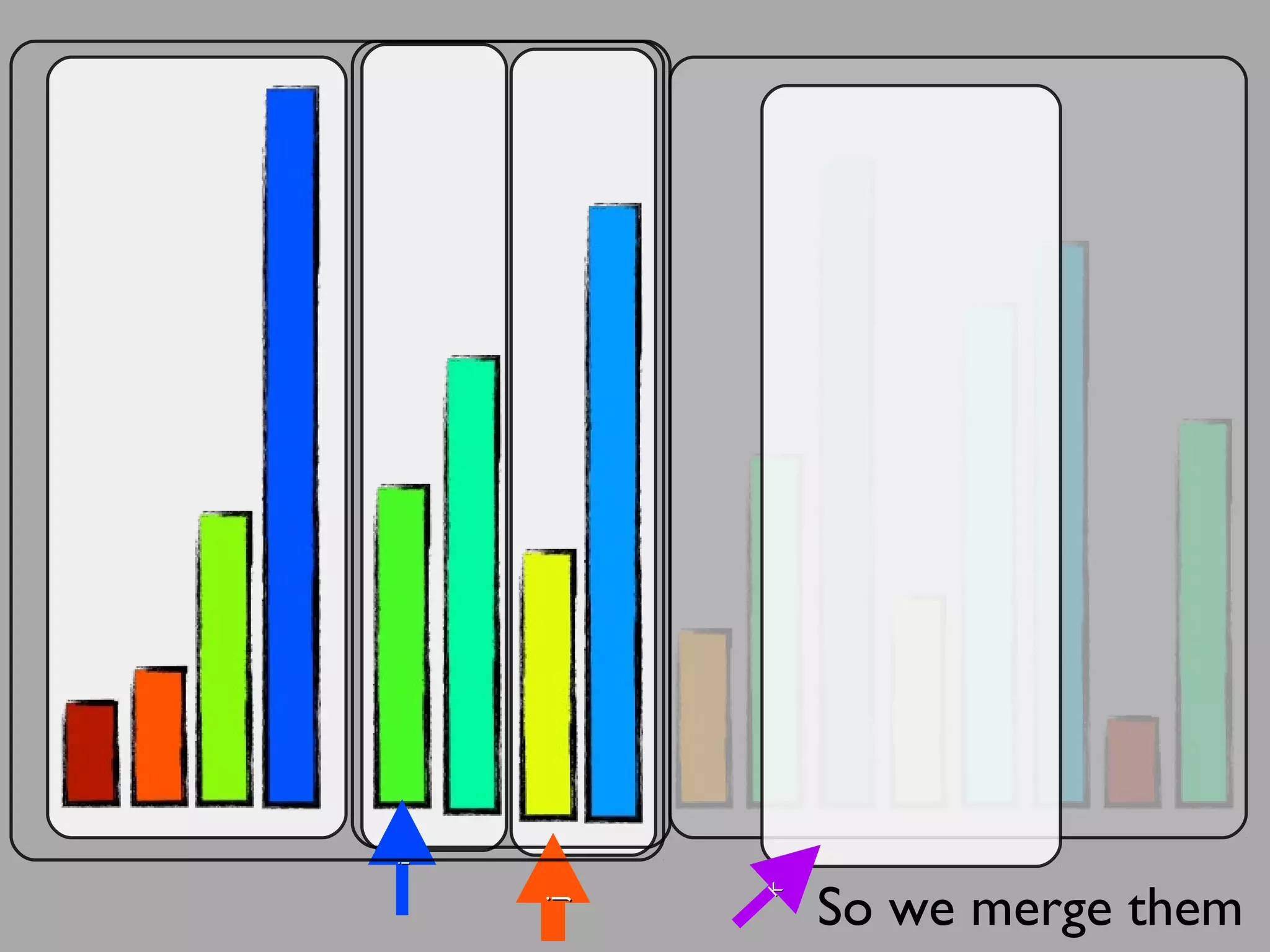
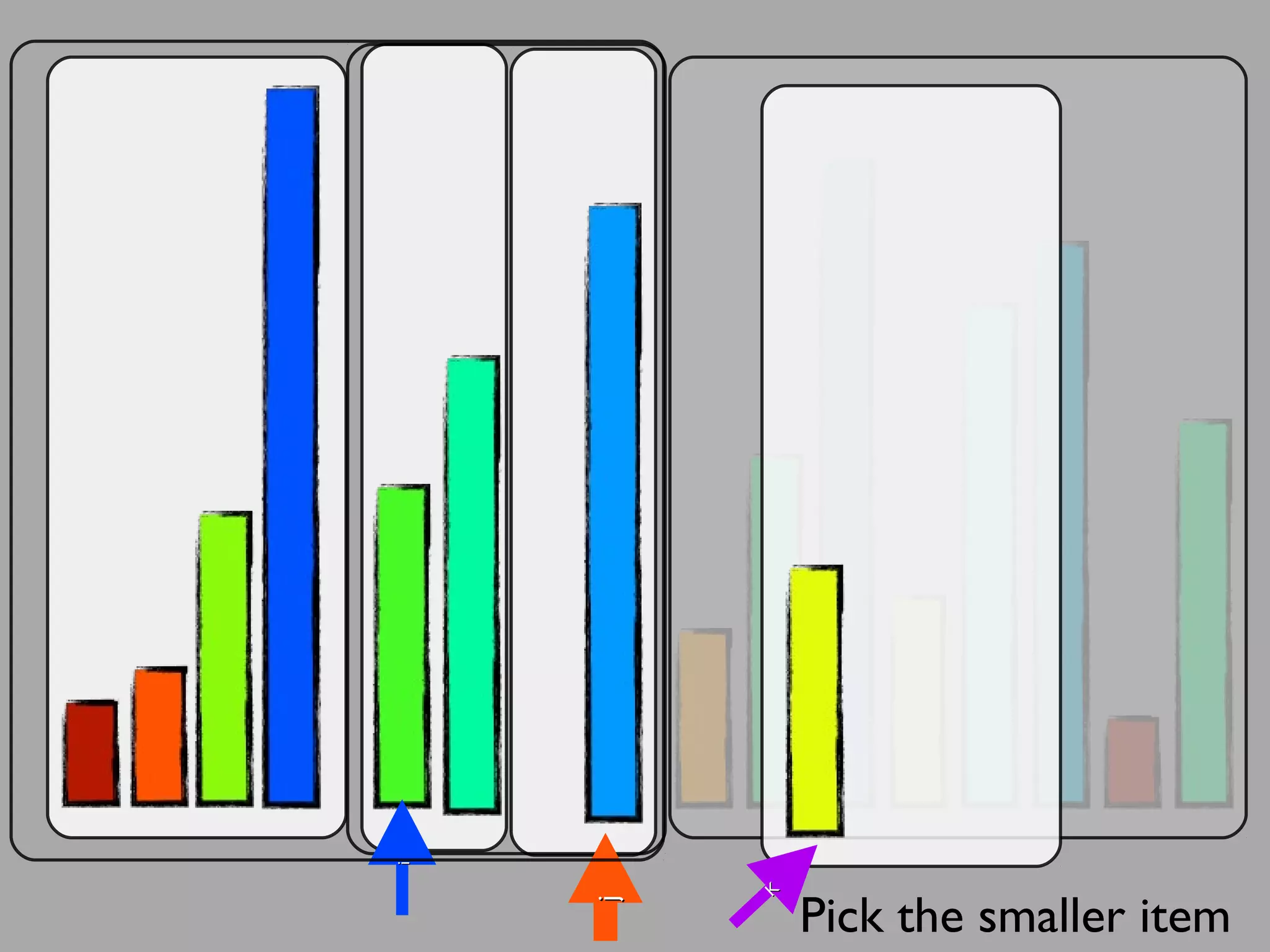
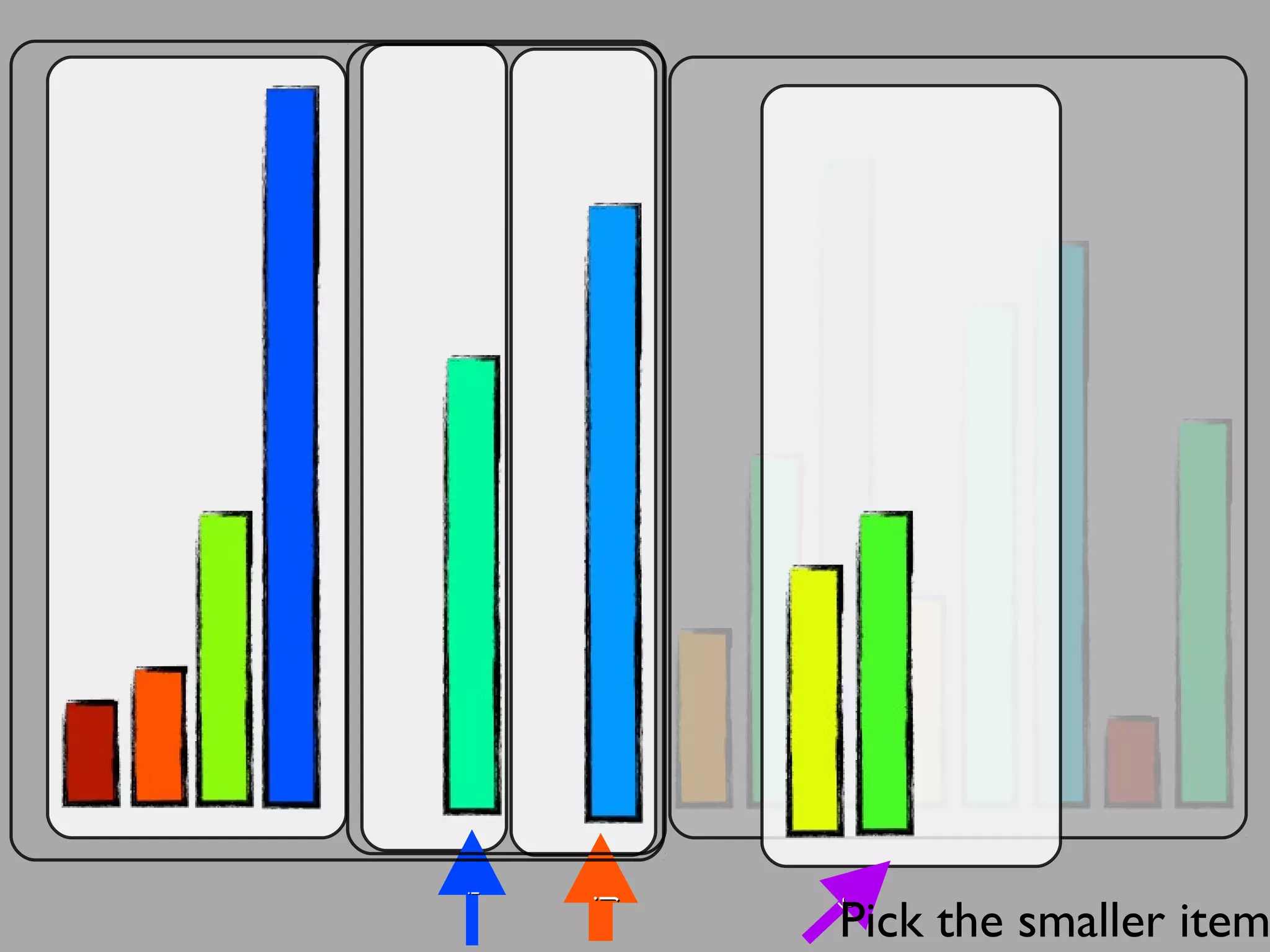
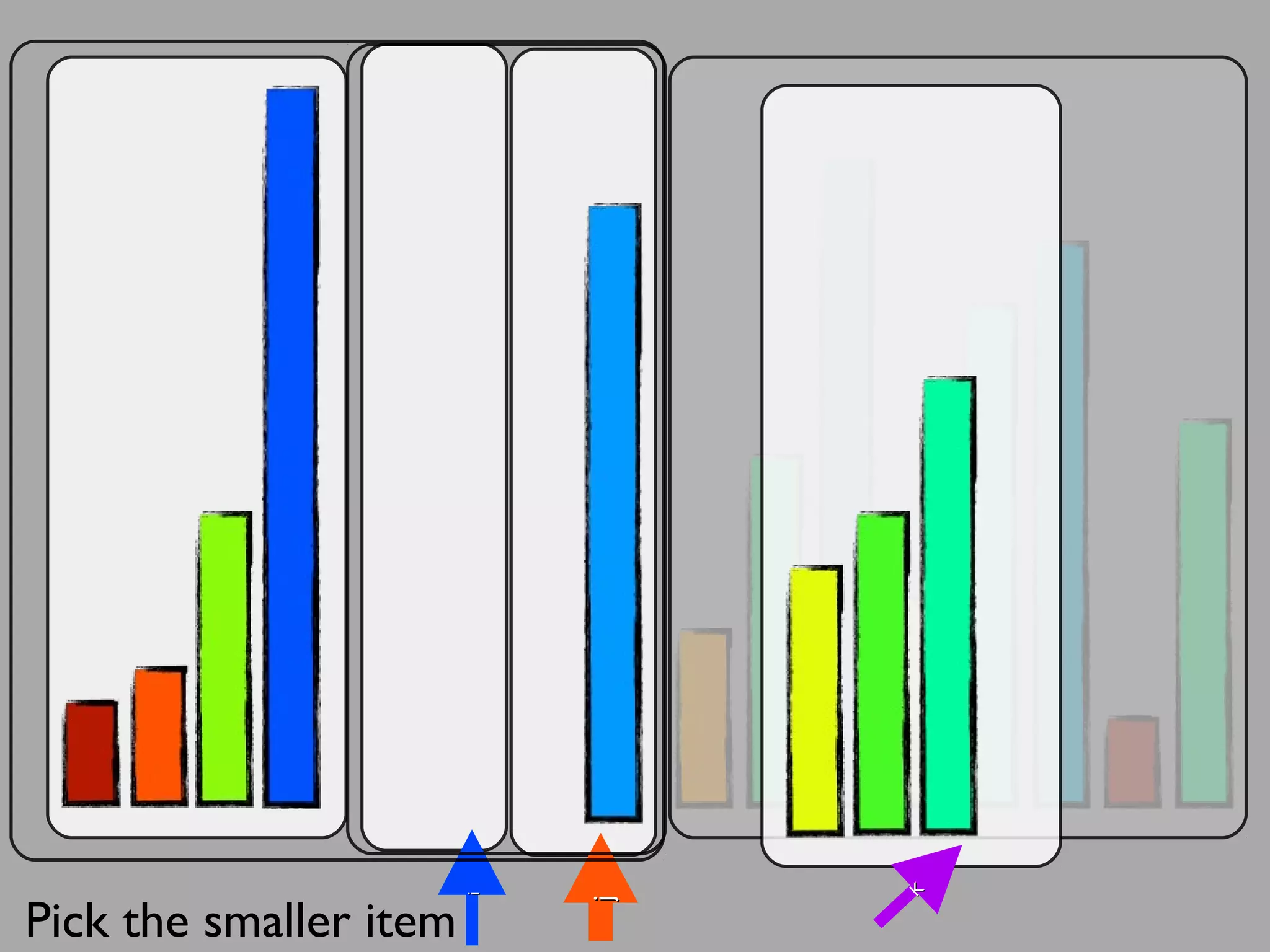
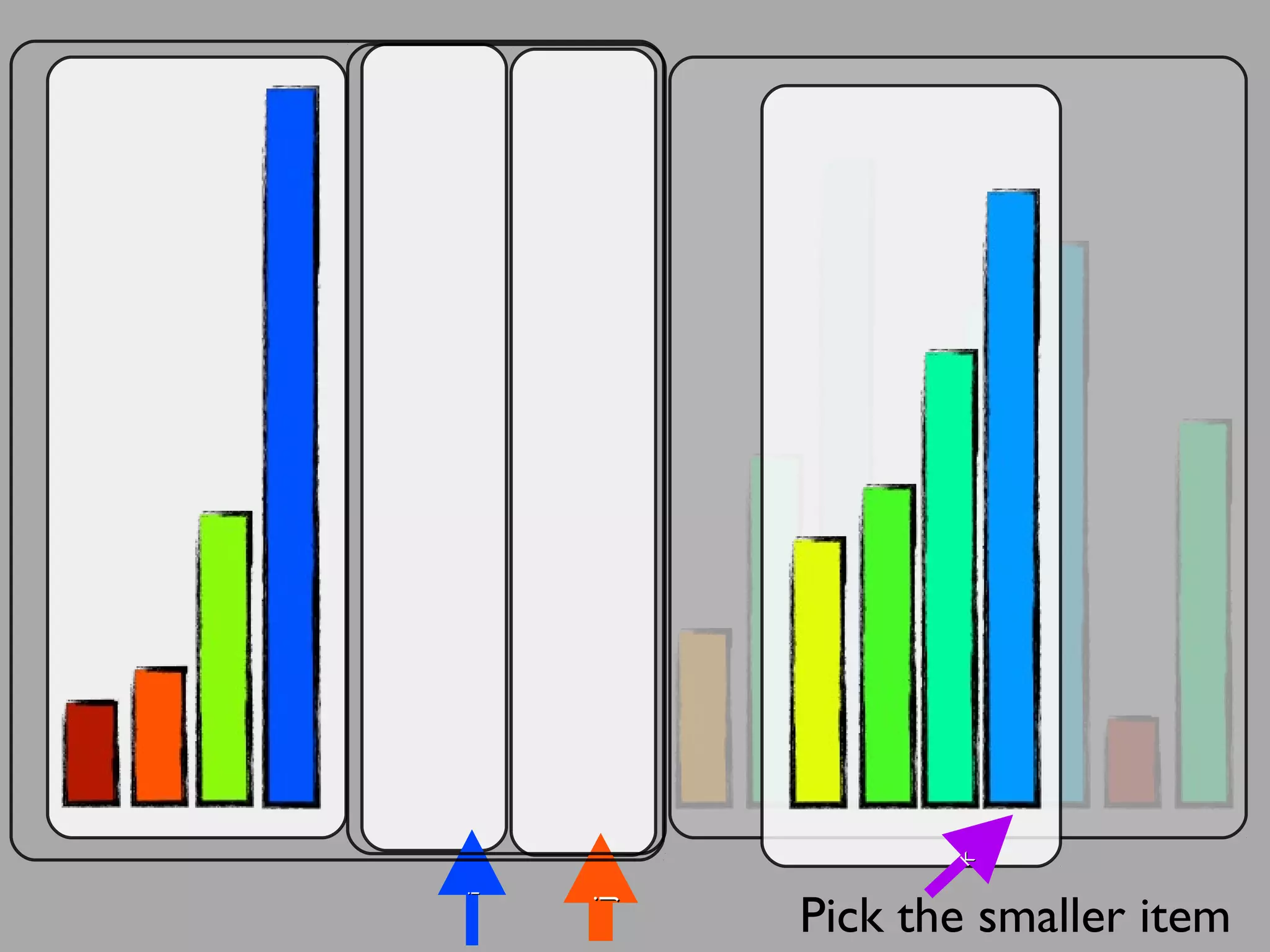
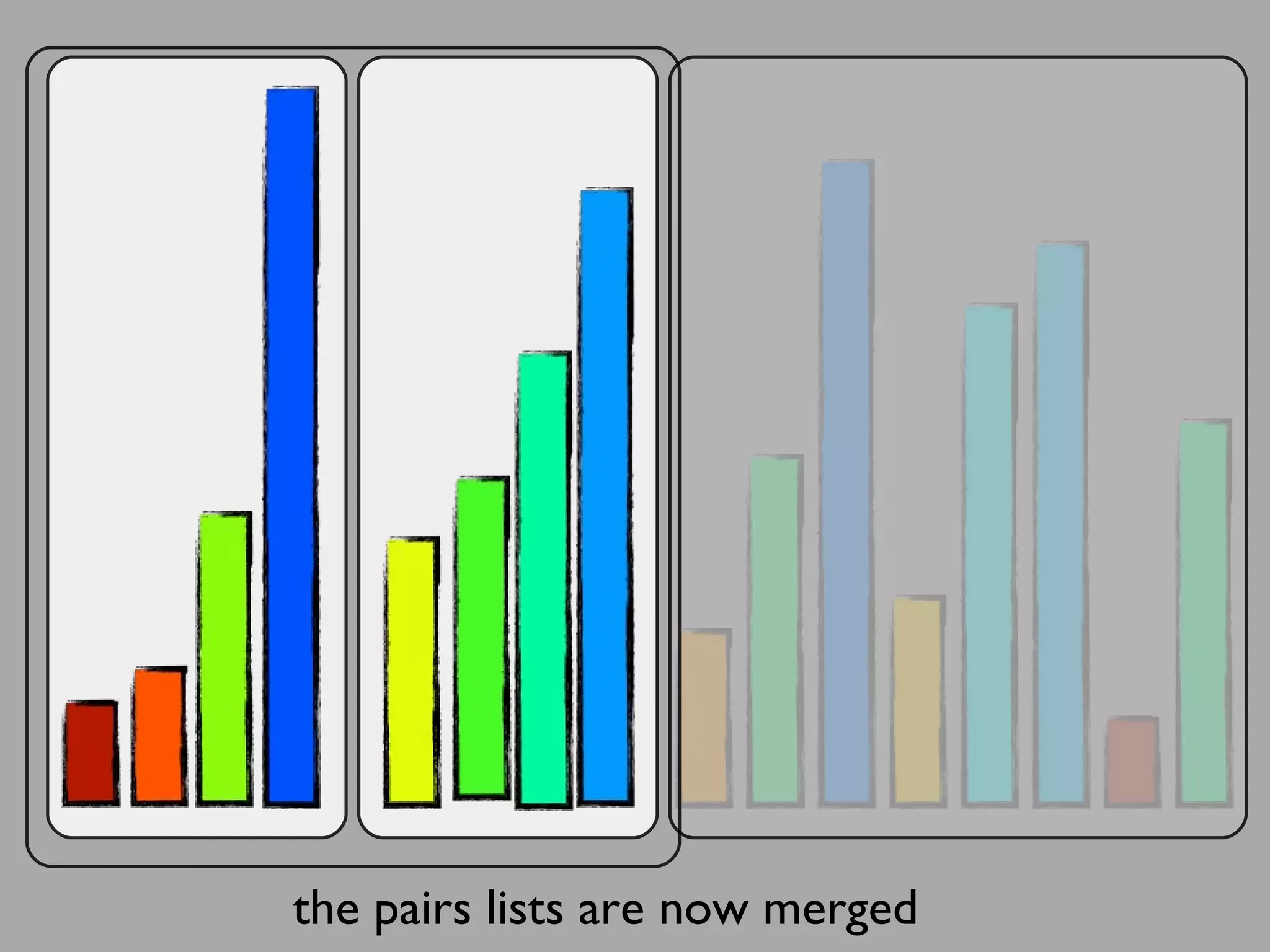
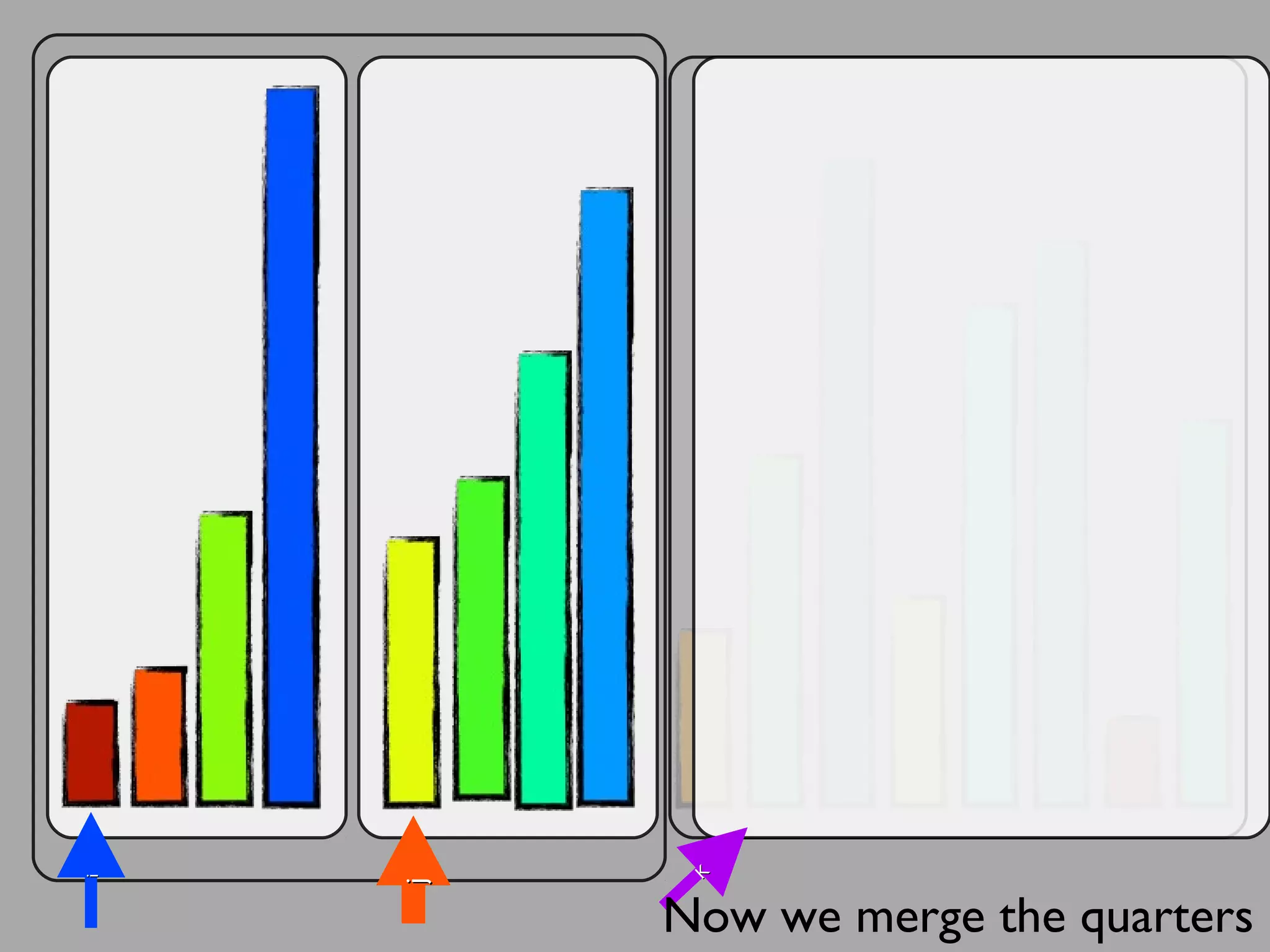
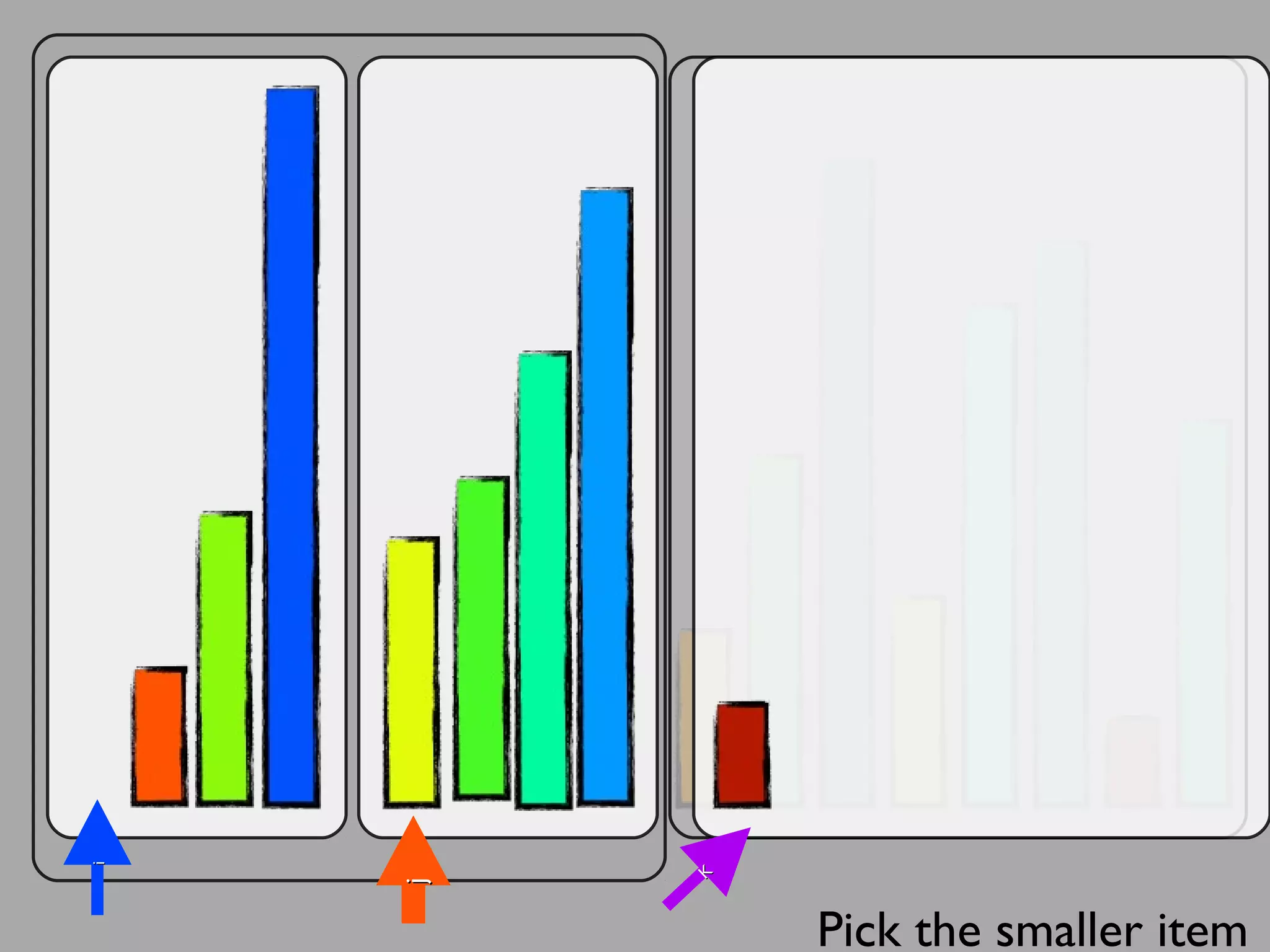
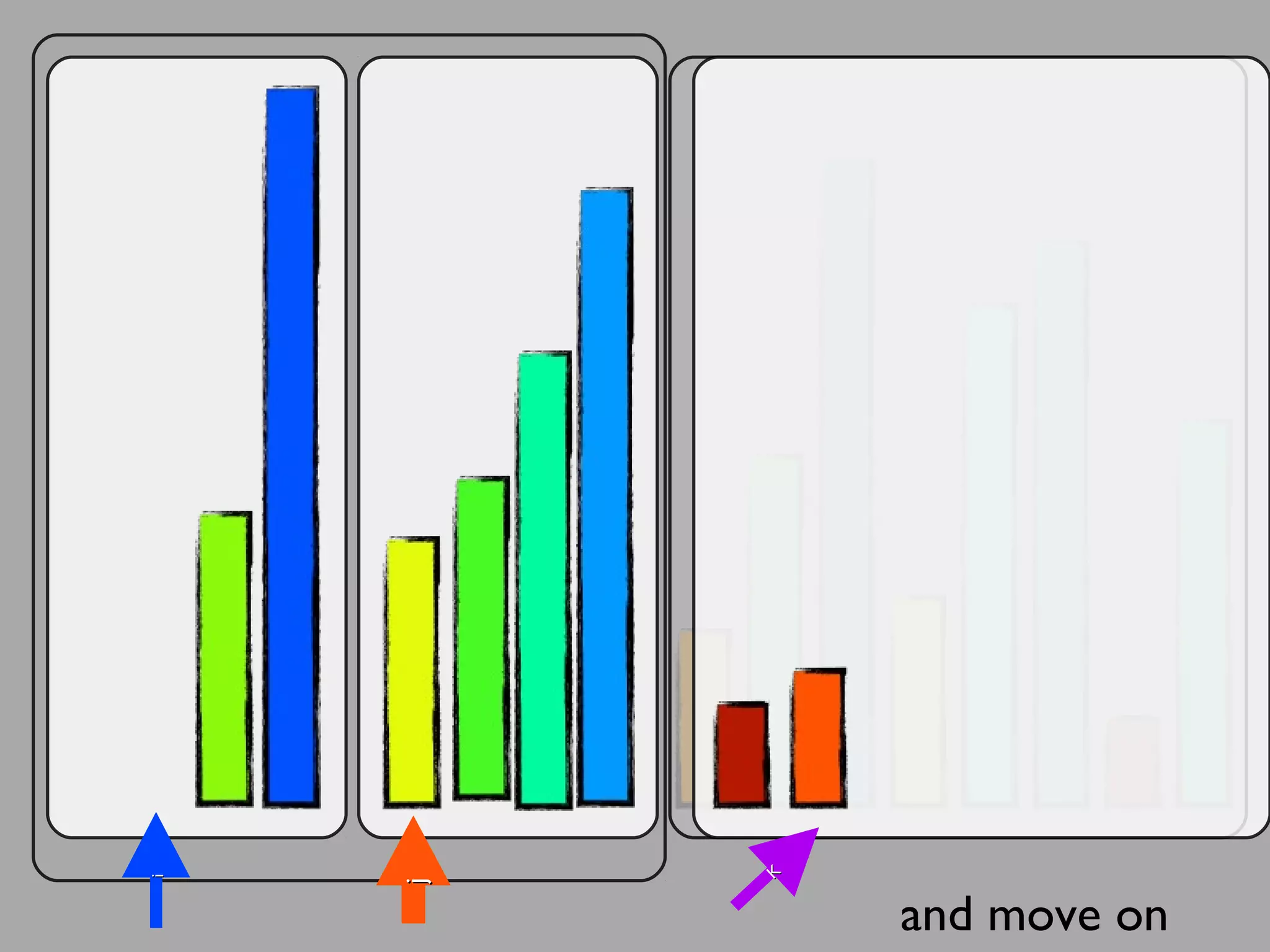
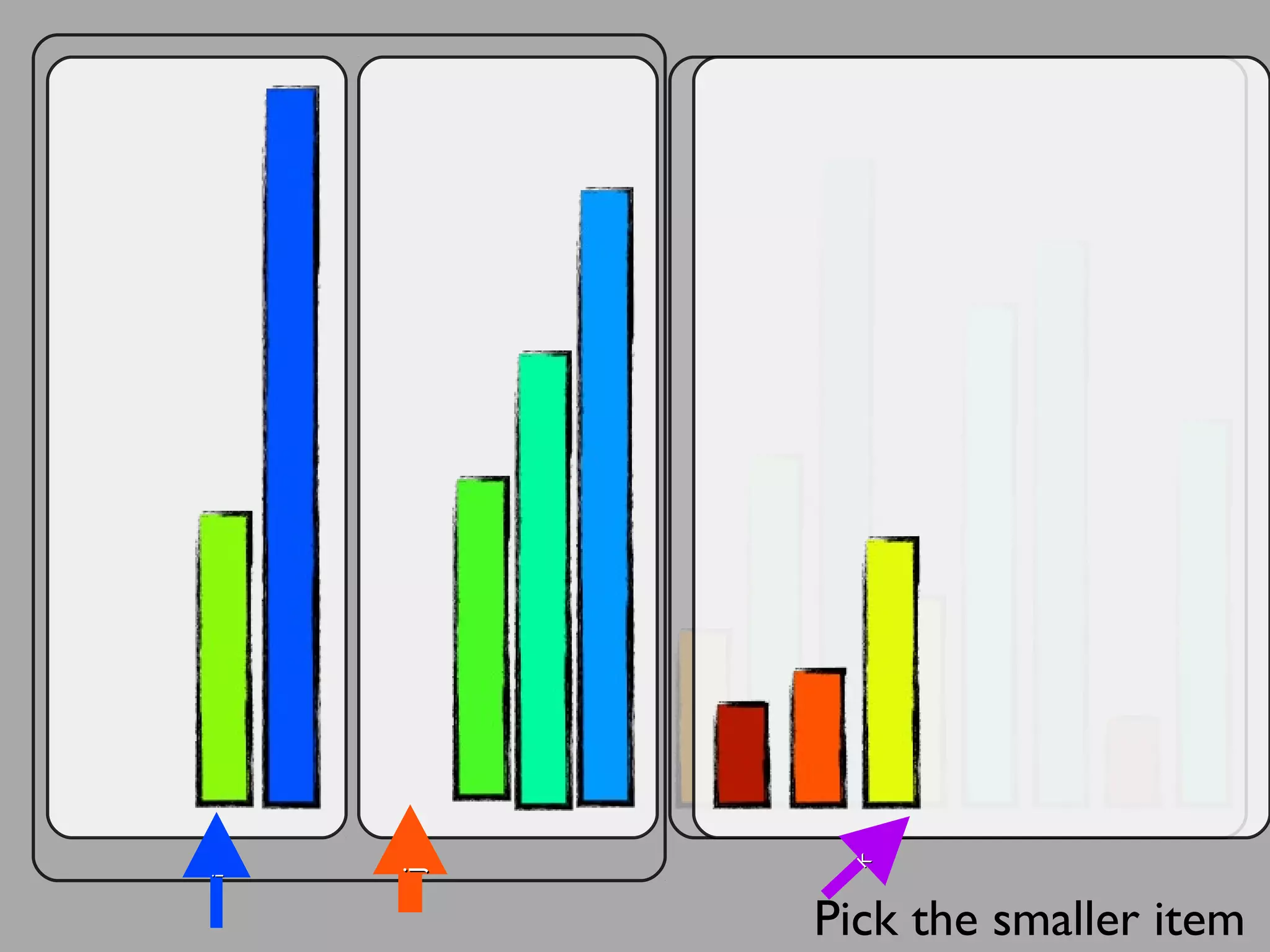
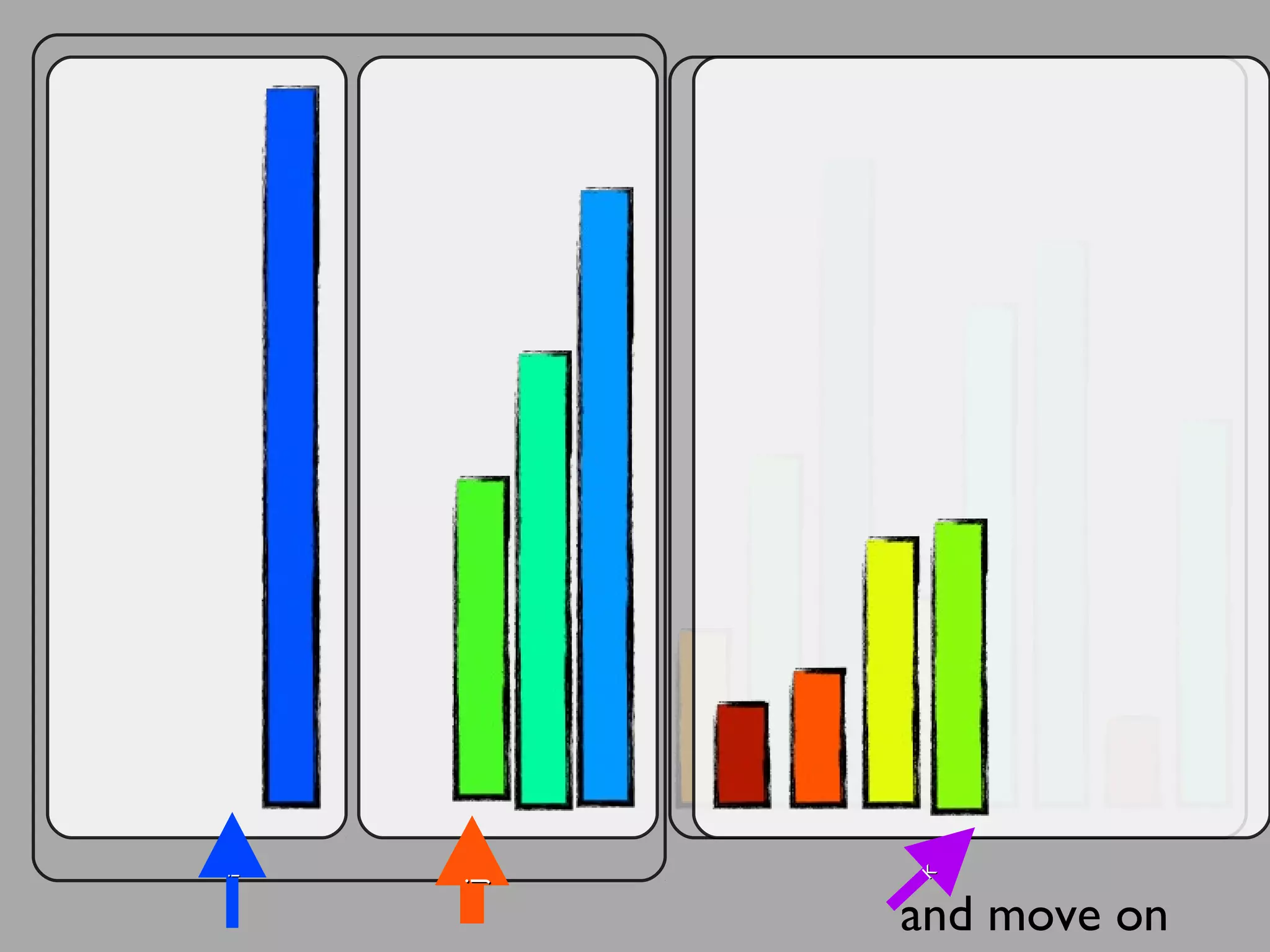
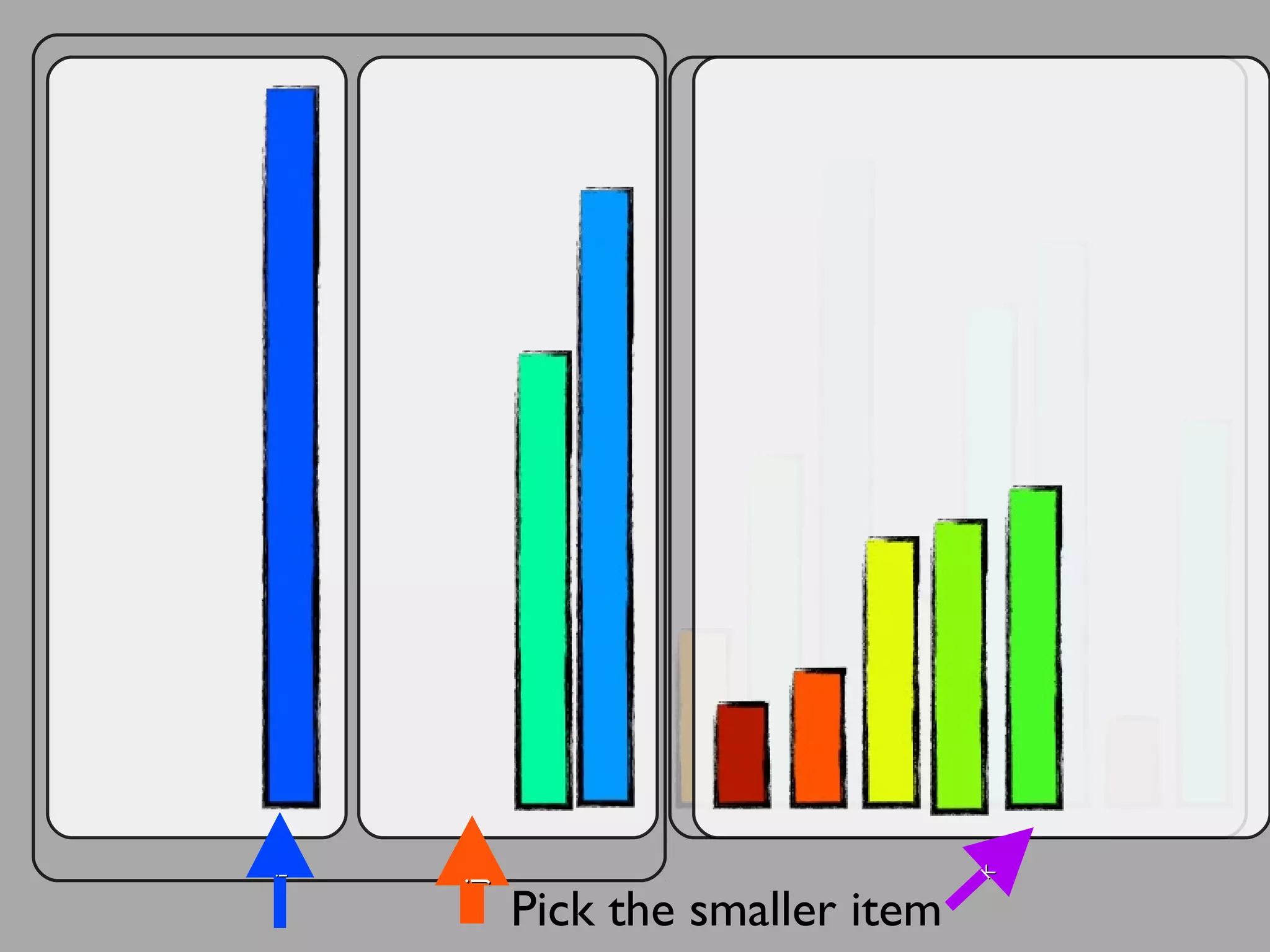
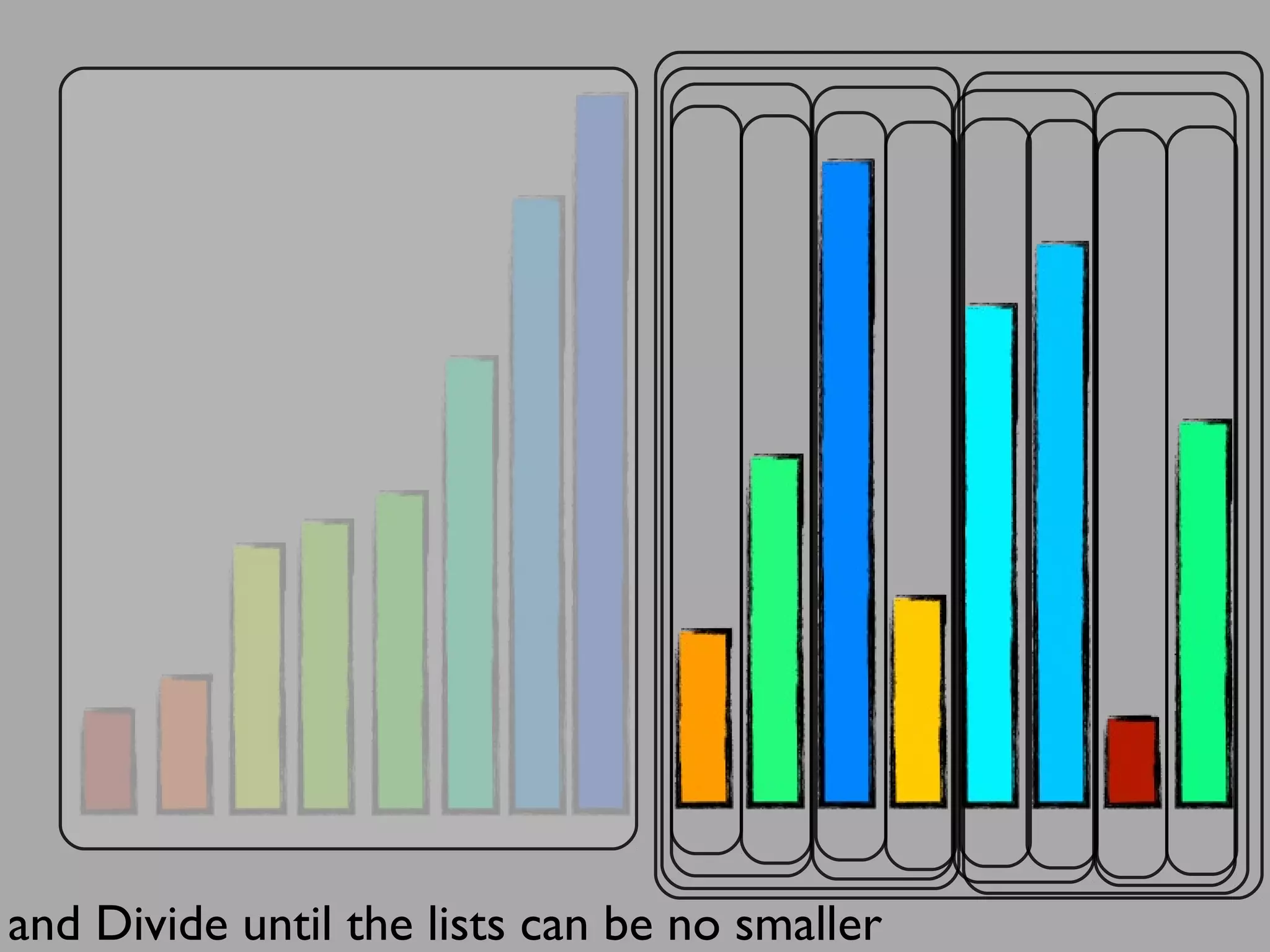
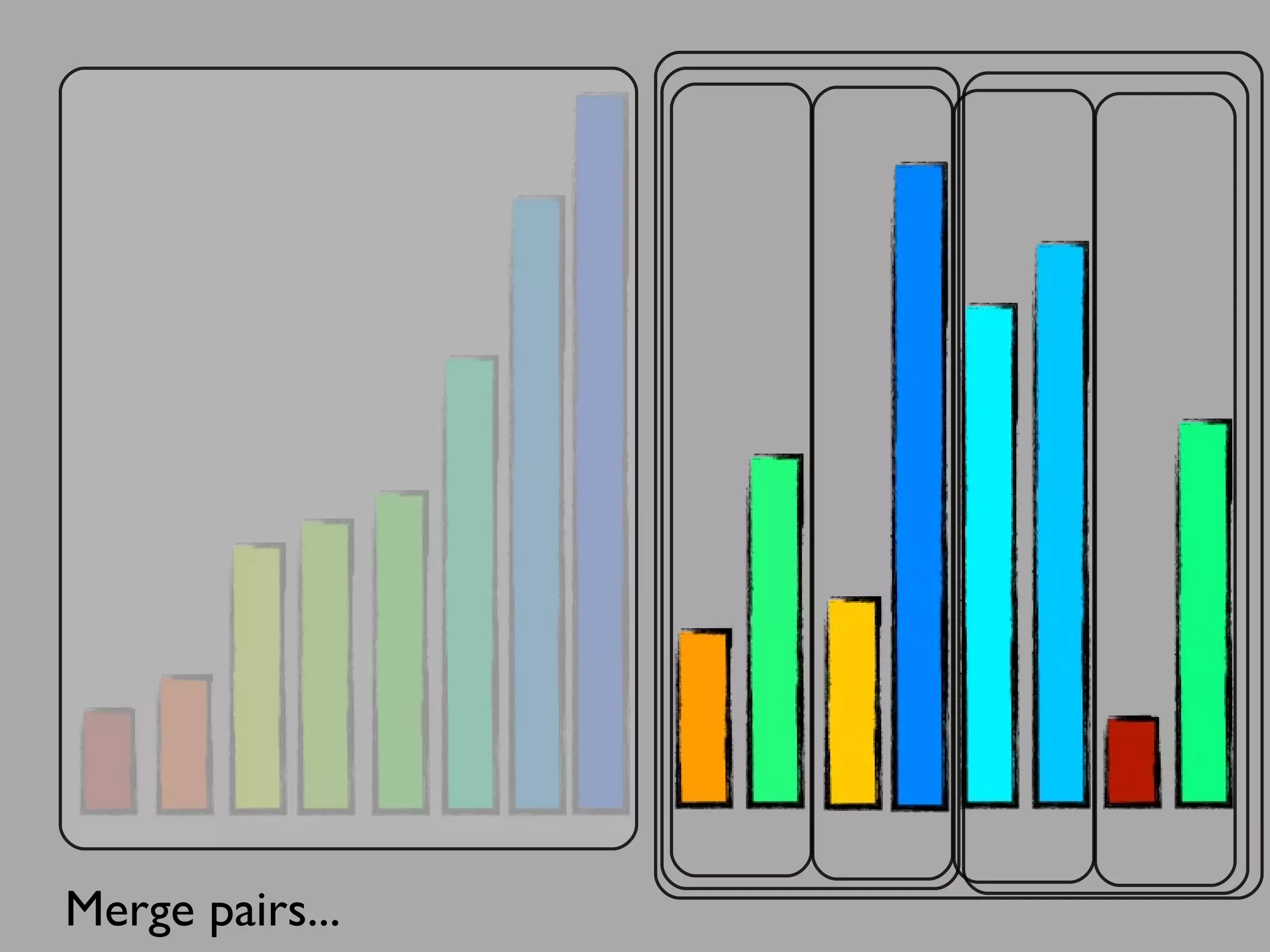
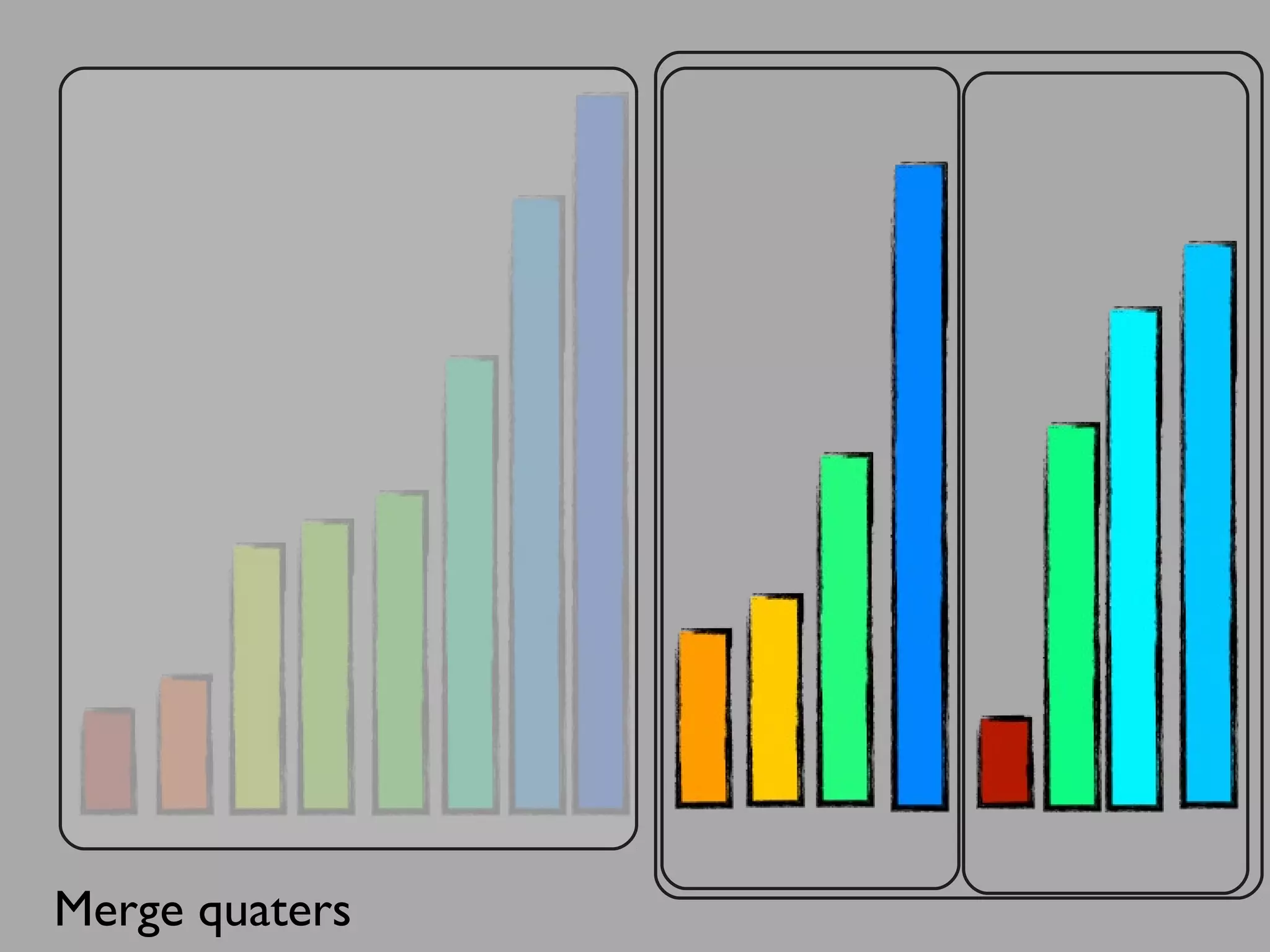
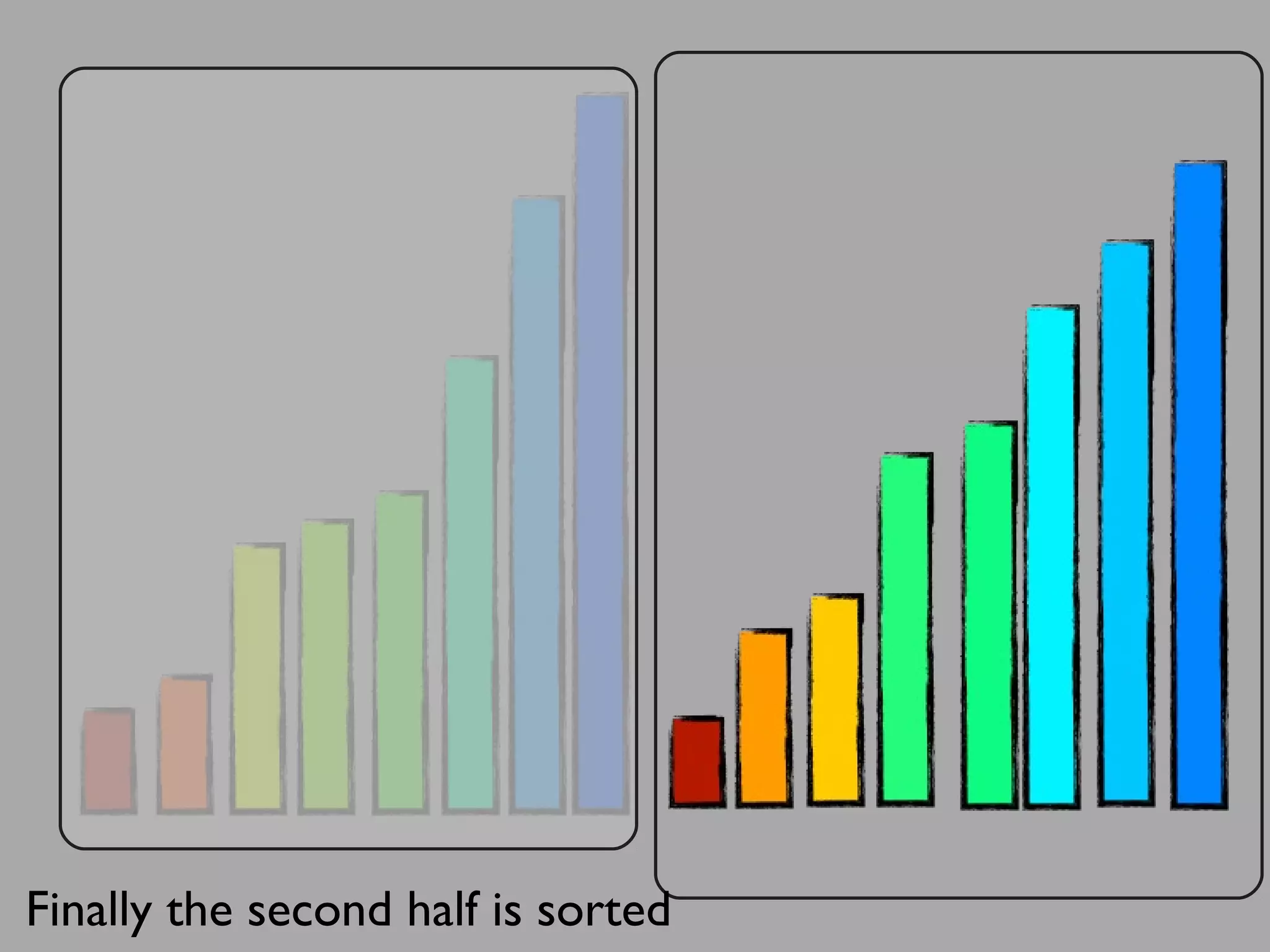
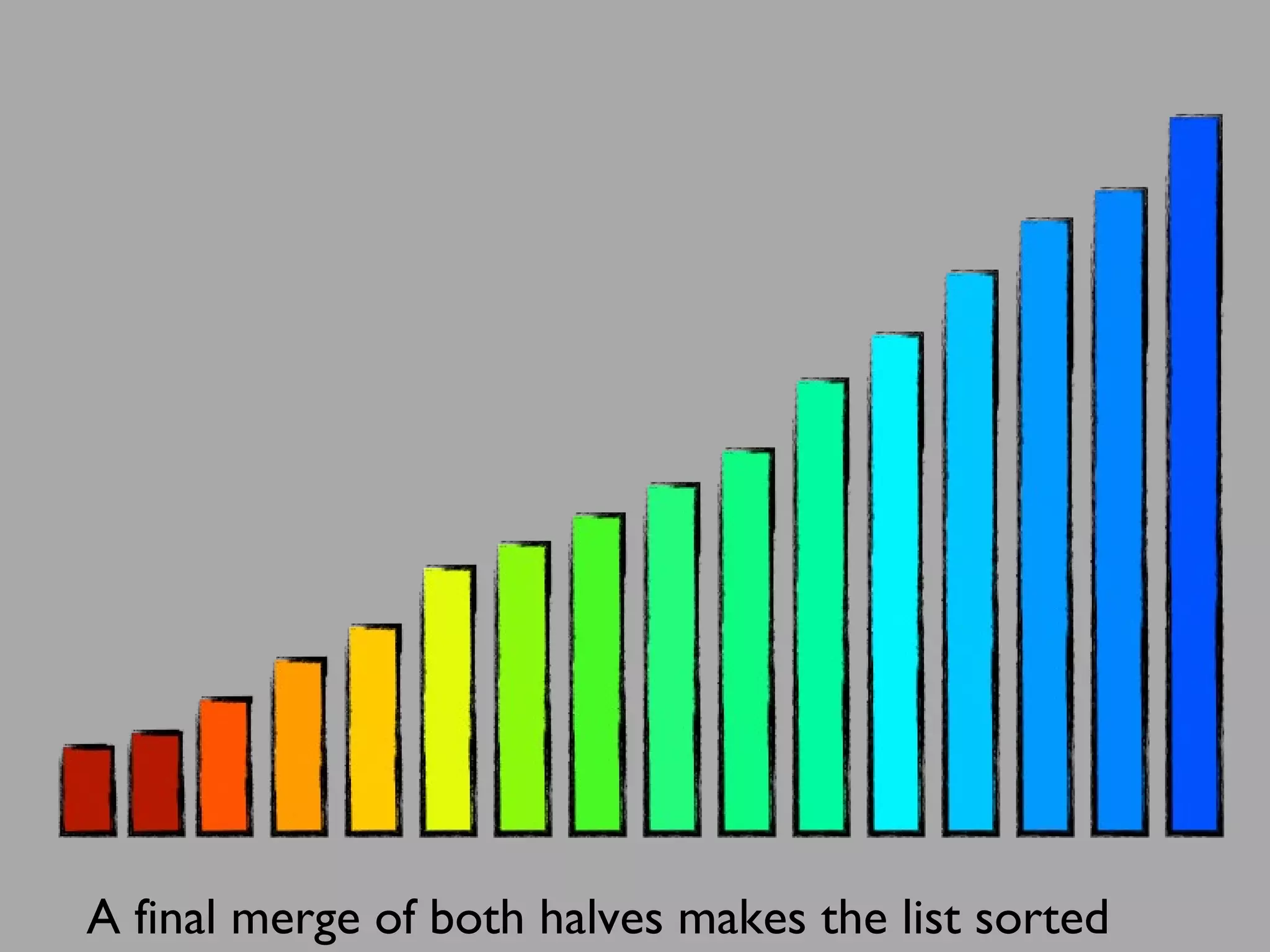
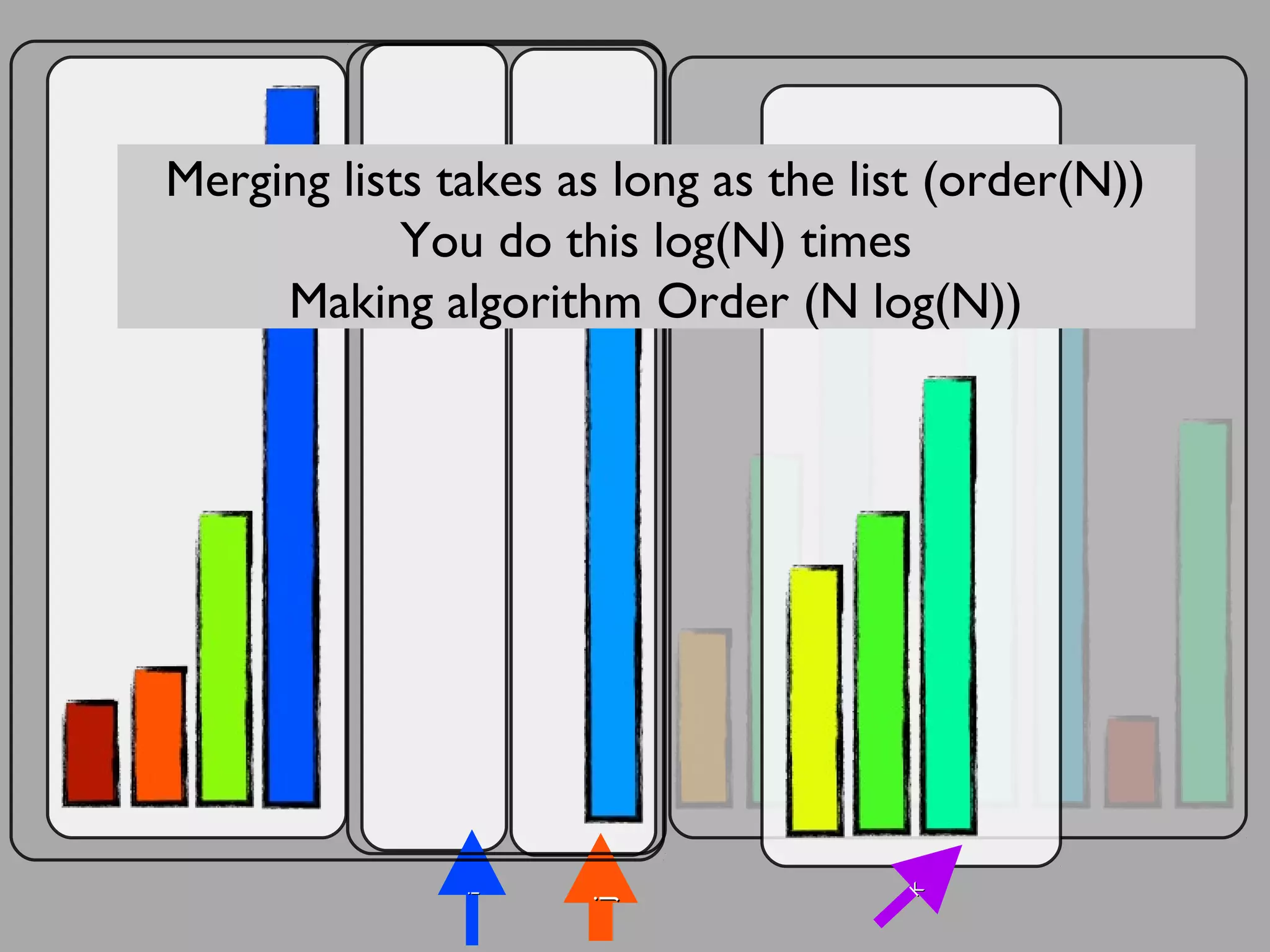
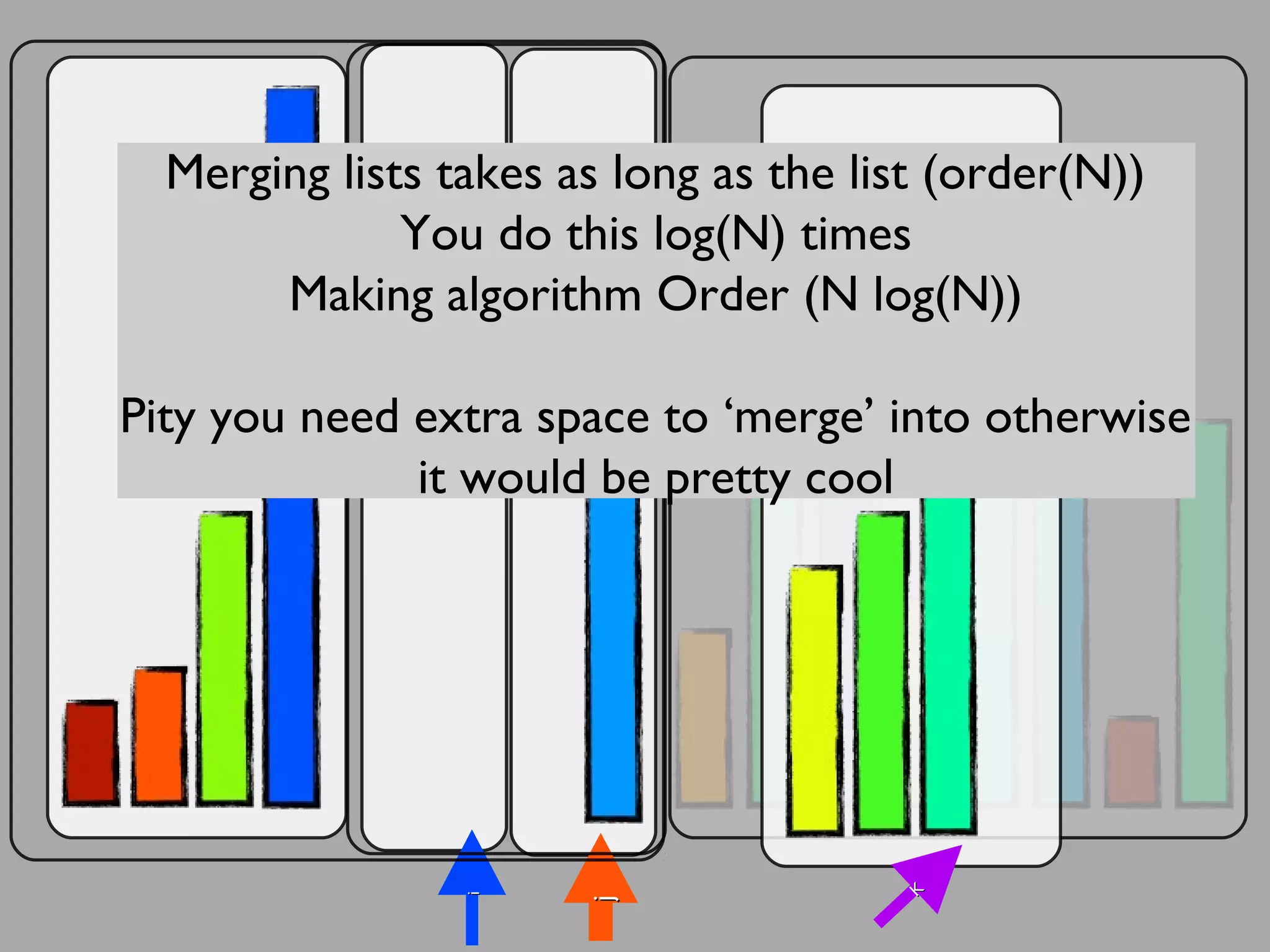
The merge sort algorithm works by recursively dividing an unsorted list into single item sub-lists and then merging those lists back together in a sorted way. It divides the target list in half repeatedly until all sub-lists contain one item. Then it merges the sub-lists back together two at a time, comparing the items in each sub-list and choosing the smaller item to build a new sorted sub-list, until the entire list is merged back in sorted order. This has an efficiency of O(n log n) time complexity because the merging step takes linear time but only needs to be done log(n) times.
Merge sort b
- 1.
- 2. Let’s start withan unsorted list
- 3. Divide the listinto two lists
- 4. Divide that listup again
- 5. Divide that listup again
- 6.
- 7. A single itemlist must be sorted✓
- 8. go to thenext list, a single item list must be sorted✓
- 9. jj ii KK Now take thatpair and merge
- 10. jj ii KK Look down bothlists taking the smallest
- 11. jj ii ✓ KK When both listsrun out you have a sorted list
- 12. jj ii Now this pairis sorted
- 13. ✓ Do thesame with the next pair
- 14. ✓ Each isa list of one item (so sorted)
- 15.
- 16. jj ii KK Creating a newsorted list
- 17. Now we havetwo lists of pairs...
- 18. So we mergethem
- 19. jj ii KK Look down bothlists taking the smallest
- 20.
- 21. jj ii KK Look down bothlists taking the smallest
- 22. jj ii KK Look down bothlists taking the smallest
- 23. jj ii KK Look down bothlists taking the smallest
- 24. jj ii KK Look down bothlists taking the smallest
- 25. the list issorted and you can begin the next quarter
- 26. A single itemlist must be sorted✓
- 27. A single itemlist must be sorted✓
- 28.
- 29.
- 30. jj ii KK When both listsrun out you have a sorted list
- 32. Sort the nextpair
- 33. A single itemlist must be sorted ✓
- 34. A single itemlist must be sorted ✓
- 35. Merge the singleitem lists
- 36.
- 37.
- 38.
- 39. Now we havetwo lists of pairs...
- 40.
- 41.
- 42.
- 43.
- 44.
- 45. the pairs listsare now merged
- 46. ii jj KK Now we mergethe quarters
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55. The first halfis now sorted
- 56. Quickly we dothe other half
- 57.
- 58.
- 59. and Divide untilthe lists can be no smaller
- 60.
- 61.
- 62. Finally the secondhalf is sorted
- 63. A final mergeof both halves makes the list sorted
- 64. ii jj KK Merging lists takesas long as the list (order(N)) You do this log(N) times Making algorithm Order (N log(N))
- 65. ii jj KK Merging lists takesas long as the list (order(N)) You do this log(N) times Making algorithm Order (N log(N)) Merging lists takes as long as the list (order(N)) You do this log(N) times Making algorithm Order (N log(N)) Pity you need extra space to ‘merge’ into otherwise it would be pretty cool
Editor's Notes
- #3 Lets begin with a list to sort
- #4 We split the array in two and look at the first half.
- #5 We split that in two and look at the first half.
- #6 We split that in two and look at the first half.
- #7 We split that in two and look at the first half. We reach a single item so it must be sorted.
- #8 We split that in two and look at the first half. We reach a single item so it must be sorted.
- #9 We look at the other half. Its also a single array so it’s also sorted.
- #10 We now have two sorted arrays which we need to merge . Using two pointers we move down them picking the smallest one each time. The final purple k pointer shows where the item will go.
- #12 When both pointer reach the end of their respective lists we have all the items merged.
- #13 So this sub list is sorted. We can move on to the other half.
- #14 We sub divide again to get another single item. Its sorted.
- #15 the other half of this pair is signle so its sorted.
- #16 We now have to merge this pair.
- #18 With these two eights done we can merge the first quarter.
- #26 With the first quarter done we can move to the second quarter.
- #56 With the first half done. I am going to speed up the process for the second half.
- #58 We split
- #59 And split
- #60 And split until we have single items.
- #61 then we merge halves together.
- #62 and merge again.
- #63 and again, until we are ready to merge with first half.
- #64 Once the final merge is complete we are done.