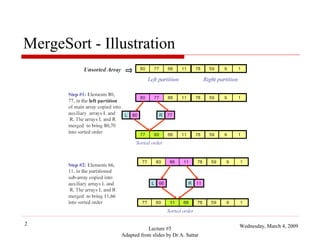
This document contains lecture slides about merge sort algorithms from a course on analysis of algorithms at Islamia College University Peshawar. It discusses illustrations of how merge sort works, provides pseudo code, analyzes the recurrence relation and time complexity, and notes that the worst and average case running times are both theta(n log n). It was presented on March 4, 2009 by instructor Mr. Zahid, adapting slides from Dr. A. Sattar.

1. Sorting Algorithms
Department of Computer Science
Islamia College University Peshawar
Fall 2012 Semester
BCS course: CS 00 Analysis of Algorithms
Course Instructor: Mr. Zahid

2. MergeSort - Illustration
2
Lecture #5
Adapted from slides by Dr A. Sattar
Wednesday, March 4, 2009

3. MergeSort – Illustration (contd…)
3
Lecture #5
Adapted from slides by Dr A. Sattar
Wednesday, March 4, 2009

4. MergeSort – Illustration (contd…)
4
Lecture #5
Adapted from slides by Dr A. Sattar
Wednesday, March 4, 2009

5. Pseudo code
5
Lecture #5
Adapted from slides by Dr A. Sattar
Wednesday, March 4, 2009

6. Pseudo code
6
Lecture #5
Wednesday, March 4, 2009

7. Recurrence Relation
 Recall for Divide and Conquer algorithms
T(n) = aT(n/b) + D(n) + C(n)
 Here a=2, and if we assume n is a power of 2, then each divide
step leads to sub-arrays of size n/2
 D(n)=θ(1)
 C(n)= θ(n)
 T(n)=2T(n/2)+θ(n)
7
Lecture #5
Adapted from slides by Dr A. Sattar
Wednesday, March 4, 2009

8. Worst-case scenario
8
Lecture #5
Adapted from slides by Dr A. Sattar
Wednesday, March 4, 2009

9. Worst and Average-case Scenario
 Worst case running time of merge sort is θ(nlgn)
 Average case running time of merge sort is also θ(nlgn)
 Best case?
9
Lecture #5
Adapted from slides by Dr A. Sattar
Wednesday, March 4, 2009

10. Worst and Average-case Scenario
 Worst case running time of merge sort is θ(nlgn)
 Average case running time of merge sort is also θ(nlgn)
 Best case?
9
Lecture #5
Adapted from slides by Dr A. Sattar
Wednesday, March 4, 2009