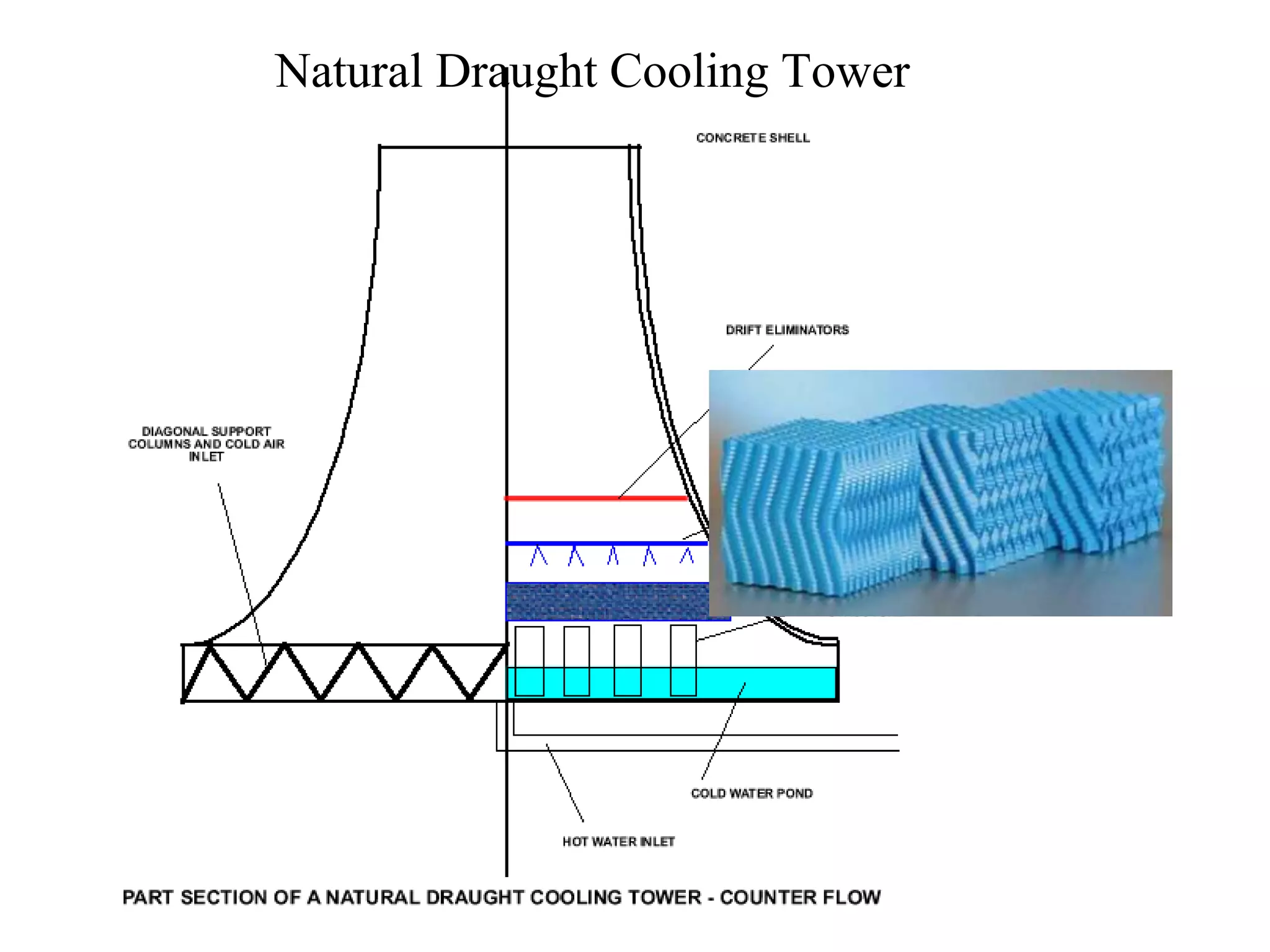
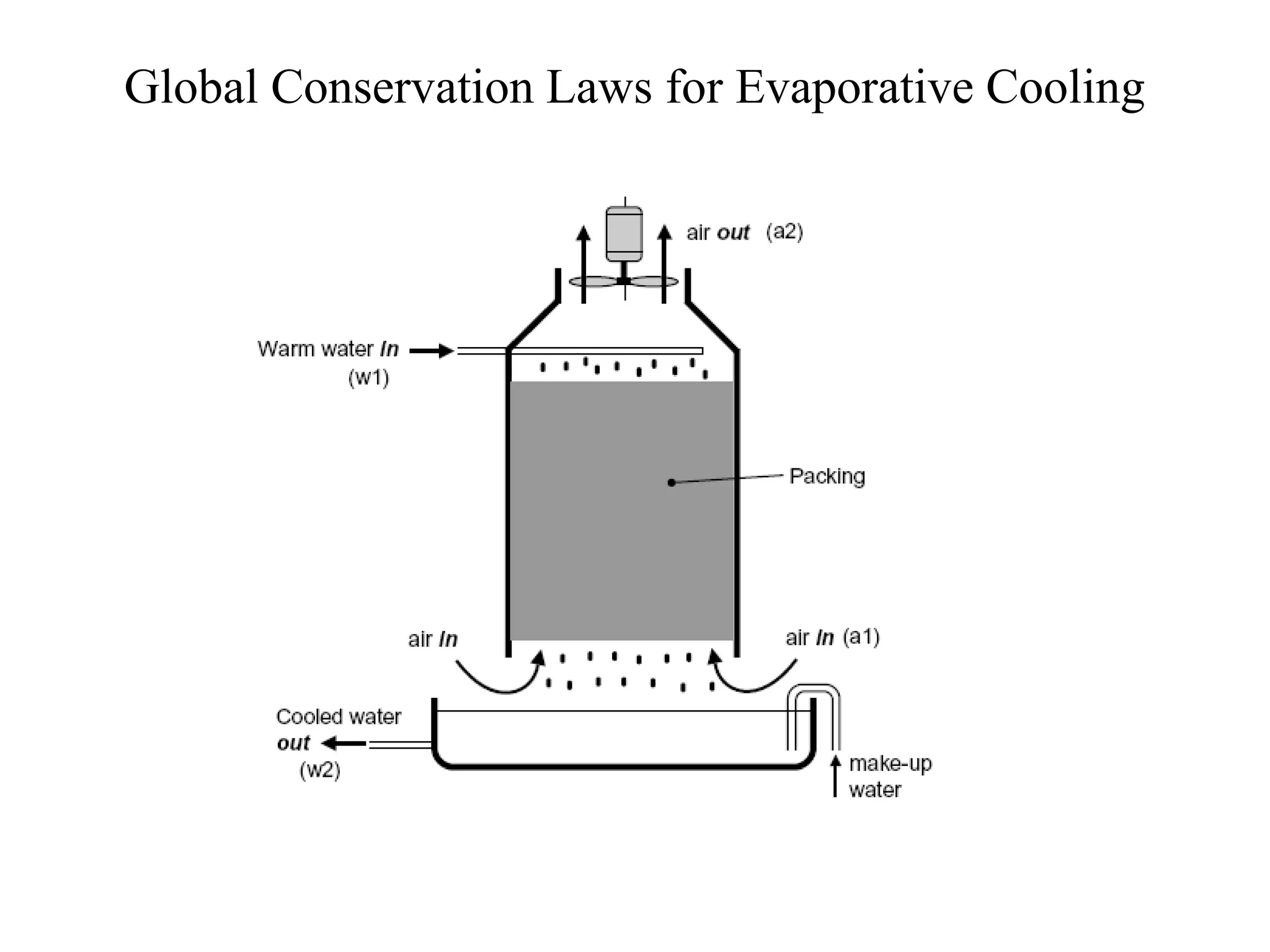
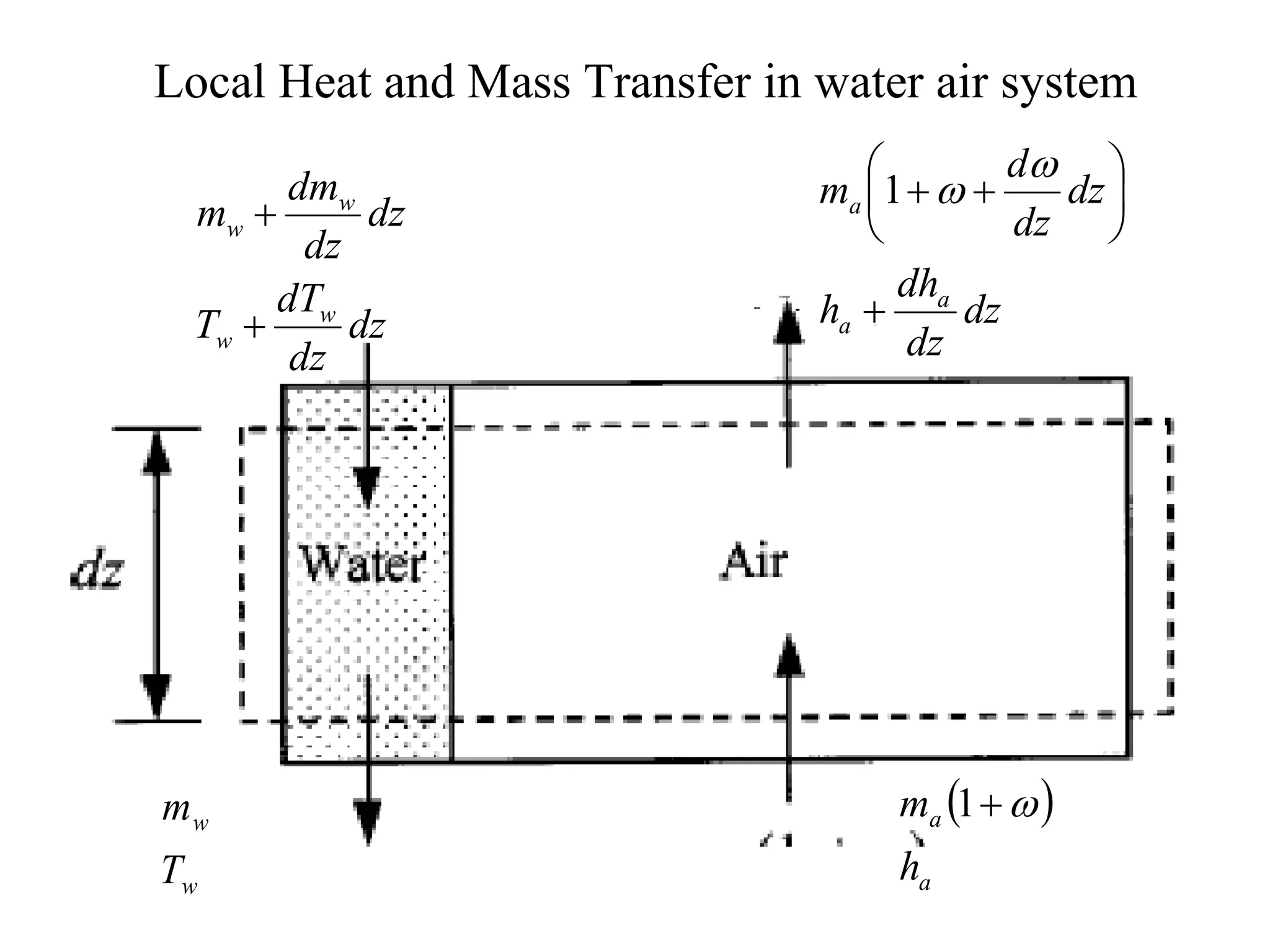
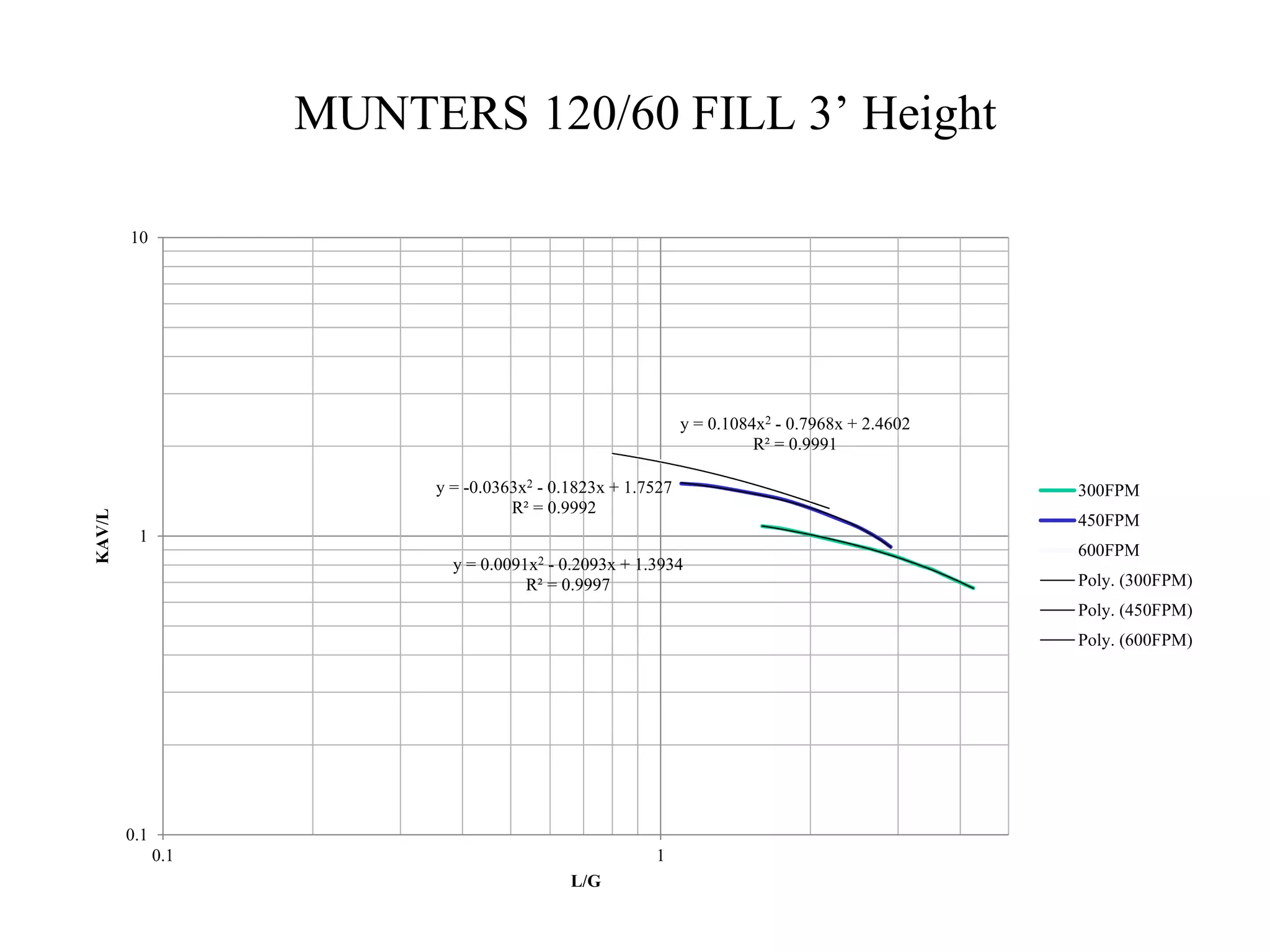
This document discusses the design and analysis of cooling towers. It begins with a brief history of cooling tower design and the development of theories to analyze them. It then discusses key parameters that describe cooling tower performance such as range, approach, and water/air ratio. The document outlines methods for analyzing cooling tower performance, including the Merkel method and global conservation equations. It also discusses factors that affect heat transfer in cooling towers and how tower characteristics are determined. Finally, it covers other important design considerations like pressure drops, fan power requirements, and water losses through evaporation and drift.

1. Thermal Analysis and Design of Cooling Towers
P M V Subbarao
Professor
Mechanical Engineering Department
I I T Delhi
Pay material for Electric Power….

2. Natural Draught Cooling Tower

3. Artistic to Scientific Design of Cooling Towers
• The art of evaporative cooling is quite ancient, although it
is only relatively recently that it has been studied
scientifically.
• Merkel developed the theory for the thermal evaluation of
cooling towers in 1925.
• This work was largely neglected until 1941 when the paper
was translated into English.
• Since then, the model has been widely applied.
• The Merkel theory relies on several critical assumptions to
reduce the solution to a simple hand calculation.
• Because of these assumptions, the Merkel method does
not accurately represent the physics of heat and mass
transfer process in the cooling tower fill.

4. Parameters of Cooling Towers
• A number of parameters describe the performance of a
cooling tower.
• Range is the temperature difference between the hot water
entering the cooling tower and the cold water leaving.
• The range is virtually identical with the condenser rise.
• Note that the range is not determined by performance of
the tower, but is determined by the heat loading.

5. • Approach is the difference between the temperature of the
water leaving the tower and the wet bulb temperature of the
entering air.
• The approach is affected by the cooling tower capability.
• For a given heat loading, water flow rate, and entering air
conditions, a larger tower will produce a smaller approach; i.e.,
the water leaving the tower will be colder.
• Water/Air Ratio (mw/ma) is the mass ratio of water (Liquid)
flowing through the tower to the air (Gas) flow.
• Each tower will have a design water/air ratio.
• An increase in this ratio will result in an increase of the
approach, that is, warmer water will be leaving the tower.
• A test ratio is calculated when the cooling tower performance
is evaluated.

6. a
v
m
m




Air
Dry
of
Flow
Mass
Vapour
Water
of
Flow
Mass

a
u
a
a
a
a
M
T
R
m
T
R
m
V
p





v
u
v
v
v
v
M
T
R
m
T
R
m
V
p

































a
v
a
v
a
v
u
a
a
u
v
v
p
p
p
p
M
M
T
R
V
p
M
T
R
V
p
M
622
.
0



Thermodynamics of Air Water Systems
Humidity Ratio:

7. Local Cooling Tower Theory
Heat is transferred from water drops to the surrounding air by the transfer of sensible and latent heat

8. Global Conservation Laws for Evaporative Cooling

9. SSSF Model for Cooling Tower
Conservation of Mass for dry air:
air
out
air
in
air m
m
m 

 
 ,
,
out
air
out
air
out
water
in
air
in
air
in
water m
m
m
m ,
,
,
,
,
,



 
 


Conservation of Mass for water:
• First Law Analysis:
      
 
fg
i
e
i
air
steam
p
i
air
p
e
air
steam
p
e
air
p
air
We
W
CWe
W
CWi
h
T
C
C
T
C
C
m
T
C
m
T
C
m Wi



 











,
,
,
,
,
,

10. Enthalpy of Wet air
   
 
fg
i
i
air
steam
p
i
air
p
fg
e
e
air
steam
p
e
air
p
air
We
W
CWe
W
CWi
h
T
C
C
h
T
C
C
m
T
C
m
T
C
m Wi



 











,
,
,
,
,
,
 
   
 
 
fg
i
air
steam
p
i
air
p
fg
e
air
steam
p
e
air
p
air
We
W
CWe
W
CWi
h
T
C
C
h
T
C
C
m
T
C
m
T
C
m Wi










,
,
,
,
,
, 

   
 
i
i
moisture
i
air
i
wetair
e
e
moisture
e
air
e
wetair
air
We
W
CWe
W
CWi
p
T
f
h
p
T
f
h
m
T
C
m
T
C
m Wi

 ,
,
(
,
,
( ,
,
,
,
,
, 








11. Local Heat and Mass Transfer in water air system
dz
dz
dT
T
dz
dz
dm
m
w
w
w
w


w
w
T
m
dz
dz
dh
h
dz
dz
d
m
a
a
a











1
 
a
a
h
m 

1

12. Local Air-side control volume of fill
 dA
T
T
h a
w 
~
dz
dz
dT
T
dz
dz
dm
m
w
w
w
w


w
w
T
m
dz
dz
dh
h
dz
dz
d
m
a
a
a











1
 
a
a
h
m 

1

13. Mechanism of Heat Transfer in Cooling Towers
• Heat transfer in cooling towers occurs by two major
mechanisms:
• Sensible heat from water to air (convection) and
• transfer of latent heat by the evaporation of water (diffusion).
• Both of these mechanisms operate at air-water boundary
layer.
• The total heat transfer is the sum of these two boundary layer
mechanisms.
• The total heat transfer can also be expressed in terms of the
change in enthalpy of each bulk phase.
• A fundamental equation o f heat transfer in cooling towers
(the Merkel equation) is obtained.
  air
air
a
sa
W
W
CW dh
m
dV
h
h
KA
dT
C
m 
 



14. The Merkel Method
• The Merkel method, developed in the 1920s, relies on
several critical assumptions to reduce the solution to a
simple manual iteration.
• These assumptions are:
• The resistance for heat transfer in the water film is
negligible,
• The effect of water loss by evaporation on energy balance
or air process state is neglected,
• The specific heat of air-stream mixture at constant pressure
is same as that of the dry air, and
• The ratio of hconv/hdiff (Lewis factor) for humid air is unity.
• Merkel combined equations for heat and water vapor
transfer into a single equation similar as

15. where:
kAV/mw = tower characteristic
k= mass transfer coefficient
A = contact area/tower volume
V = active cooling volume/plan area
mw = water flow rate
T1 = hot water temperature
T2 = cold water temperature
T = bulk water temperature
hsa = enthalpy of saturated air-water vapor mixture at bulk water temperature
(J/kg dry air)
ha = enthalpy of air-water vapor mixture (J/kg dry air )
 


1
2
T
T a
sa
w
M
h
h
dT
m
kAV
Me


16. Temperature Enthalpy Diagram of Air Water System

17. Tower Characteristics
• Tower Characteristic (MeM or NTU) is a characteristic of
the tower that relates tower design and operating
characteristics to the amount of heat that can be
transferred.
• For a given set of operating conditions, the design
constants that depend on the tower fill.
• For a tower that is to be evaluated using the characteristic
curve method, the manufacturer will provide a tower
characteristic curve.
n
a
w
m
m
C
NTU










18. Charts for Merkel Number
M
Me

19. Height of Natural Draught Cooling Toer

20. Forced Draught Cooling Towers

21. SUPPLY TOWER CHARACTERISTIC
• The supply tower characteristic of the cooling tower can be
evaluated with the help of cooling tower fill characteristics
curves provided by manufacturer which takes into account
the effect of rain and spray zones as well as fill fouling.
• These curves are certified by the cooling tower institute.

22. MUNTERS 120/60 FILL 4’ height
y = 0.0319x3 - 0.2744x2 + 0.5551x + 0.9513
R² = 0.9991
y = 0.0323x3 - 0.1391x2 - 0.2112x + 2.142
R² = 0.9993
y = 0.3571x3 - 1.4916x2 + 1.2957x + 2.0147
R² = 0.9991
0.1
1
10
0.1 1
KAV/L
L/G
300FPM
450FPM
600FPM
Poly. (300FPM)
Poly. (450FPM)
Poly. (600FPM)

23. MUNTERS 120/60 FILL 3’ Height
y = 0.0091x2 - 0.2093x + 1.3934
R² = 0.9997
y = -0.0363x2 - 0.1823x + 1.7527
R² = 0.9992
y = 0.1084x2 - 0.7968x + 2.4602
R² = 0.9991
0.1
1
10
0.1 1
KAV/L
L/G
300FPM
450FPM
600FPM
Poly. (300FPM)
Poly. (450FPM)
Poly. (600FPM)

24. Generalized Equation for Cooling Tower Supply
• A generalized equation for cooling tower supply can be
developed from the manufacturer curves (known as the
supply equation) and is of the form:
m
a
w
n
air
m
m
u
C
L
KAV












25. Air Side Pressure Drop
• Manufacturer pressure drop curves are available
for pressure drops at the inlet louvers, drift
eliminators and the fill packing.
• These curves are shown in the following slides.
• Using curve fitting software, generalized pressure
drop equations are found developed so as to
calculate the pressure drops.

26. y = 3E-07x2 - 9E-06x + 0.0031
R² = 0.9998
0
0.1
0.2
0.3
300 400 500 600 700 800
PRESSURE
DROP
,in
WC
AIR VELOCITY, FPM
PRESSURE DROPACROSS DRIFT ELIMINATOR
Series1
Poly. (Series1)

27. 0
0.1
0.2
0.3
300 400 500 600 700 800 900 1000 1100 1200
PRESSURE
DROP
,
in
WC
AIR VELOCITY,FPM
PRESSURE DROPACROSS INLET LOUVERS
Series1

28. PRESSURE DROP ACROSS
FILL
0.02
0.2
2
300
wl4
wl6
wl8
wl11
BRENTWOOD 1900 FILL OF 4FT FILL HEIGHT

29. BHP OF THE FAN
• The total pressure drop (PD) across the cooling
tower which is the summation of the pressure
drops across the drift eliminators, inlet louvers and
the fill packing (constituting the static pressure
drop) and also the velocity pressure drop is
calculated.
• Now, the total fan power required is calculated as
BHP = (CFM * PD)/ (n * 6356)
where n is the efficiency of the fan.

30. ANOTHER METHOD
• We can also map the demand curve foe
varying KAV/L values with varying L/G on
the manufacturers curves for tower
characteristics in order to find the L/G ratio
of the cooling tower.
• After obtaining the L/G ratio all the steps to
be followed are same as the previous
method.

31. Loss of Water
• Evaporation Rate is the fraction of the circulating water
that is evaporated in the cooling process.
• A typical design evaporation rate is about 1% for every
12.5C range at typical design conditions.
• It will vary with the season, since in colder weather there is
more sensible heat transfer from the water to the air, and
therefore less evaporation.
• The evaporation rate has a direct impact on the cooling
tower makeup water requirements.

32. • Drift is water that is carried away from the tower in the form
of droplets with the air discharged from the tower.
• Most towers are equipped with drift eliminators to minimize
the amount of drift to a small fraction of a percent of the water
circulation rate.
• Drift has a direct impact on the cooling tower makeup water
requirements.
• Recirculation is warm, moist air discharged from the tower
that mixes with the incoming air and re-enters the tower.
• This increases the wet bulb temperature of the entering air and
reduces the cooling capability of the tower.
• During cold weather operation, recirculation may also lead to
icing of the air intake areas.