Dokumen membahas mengenai matriks kekakuan dan matriks fleksibilitas yang digunakan dalam analisis struktur untuk menentukan gaya dalam dan deformasi. Disebutkan juga prosedur perhitungan serta hubungan antara gaya, deformasi, dan kondisi kesetimbangan dalam sistem struktur. Metode ini mencakup konsep derajat kebebasan, pemisahan matriks, dan transformasi koordinat.

1. MATRIKS KEKAKUAN Vs MATRIKS FLEKSIBILITY
• MATRIKS KEKAKUAN :
[ P ] = { K } [ D ] [P] : Matriks Gaya
{ K } : Matriks Kekakuan
[ D ] : Matriks Deformasi
Analisis dimulai dari lendutan , shg urutan kerjanya :
1. Syarat Kompabilitas, mencari hubungan antara deformasi dengan perpindahan titik
dalam struktur
2. Hubungan Tegangan dan regangan akibat deformasi
3. Kesetimbangan Gaya luar dan gaya dalam
• MATRIKS FLEKSIBILITY :
[D ] = {F } [P ] [ D ] : Matriks Deformasi
{ F } : Matriks Fleksibility
[ P ] : Matriks Gaya
Analisis dimulai dari Gaya , shg urutan kerjanya :
1. Kesetimbangan : Menghitung gaya dalam yang timbul akibat bekerjanya Gaya luar
2. Hubungan Tegangan dan regangan akibat Gaya dalam
3. Syarat Kompabilitas, mencari hubungan antara deformasi dengan perpindahan titik
dalam struktur

2. Metode Matriks kekakuan
• DERAJAT KETIDAKTENTUAN KINEMATIS/DERAJAT KEBEBASAN : DOF
Suatu besaran yang menyatakan jumlah komponen bebas dari lendutan di titik kumpul yang mungkin terjadi
sehubungan dengan bekerjanya beban.
A. DERAJAT KEBEBASAN ROTATIONAL
Jepit : 0 DOF Sendi : 1 DOF Rol : 2 DOF
DOF = 3
STRUKTUR BALOK

3. STRUKTUR PORTAL TAK BERGOYANG
DOF = 6
STRUKTUR RANGKA BATANG
DOF = 10

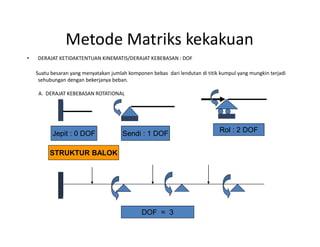
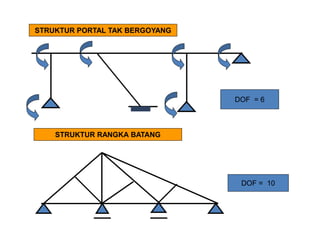
4. STRUKTUR PORTAL BERGOYANG
DOF TOTAL = DOF ROTATIONAL + DOF TRANSLASI
NP = NPR + NPS NPS = 2 NJ - [ 2 ( NFS + NHS ) + NRS + NM ]
NJ : NUMBER OF JOINT
NFS ; NUMBER OF FIX SUPPORT
NHS : NUMBER OF HINGED SUPPORT
NRS : NUMBER OF ROLLER SUPPORT
NM : NUMBER OF MEMBER
NPR = 14
NPS = 2.16 – { 2(5)+0+19}
NPS = 3
NP = NPR + NPS
NP = 17
DERAJAT KEBEBASAN TRANSLASI

5. METODE MATRIKS KEKAKUAN
1. MATRIKS KEKAKUAN KEBEBASAN SESUNGGUHNYA
Kekakuan Struktur diperoleh melalui perkalian matriks yang diperoleh melalui :
- Hubungan Keseimbangan Gaya luar [ P ] dan Gaya Dalam [ SR ] [ B ] = [ A ]T
- Hubungan Gaya Dalam [ SR ] dan Deformasi batang [d] [ S ]
- Hubungan Gaya Lendutan [ D ] dan Deformasi batang [ d ] [ A ]
2. MATRIKS KEKAKUAN SUPERPOSISI LANGSUNG
Kekakuan Struktur diperoleh secara langsung melalui hubungan Gaya dalam dan
Deformasi yang terjadi pada batang secara keseluruhan

6. MATRIKS KEKAKUAN KEBEBASAN SESUNGGUHNYA
• PROSEDURE PERHITUNGAN
1. TENTUKAN DERAJAT KEBEBASAN STRUKTUR
DOF = 3
2. TETAPKAN PARAMETER STRUKTUR
A. STRUKTUR DASAR YANG DIKEKANG
D2
D1 D3

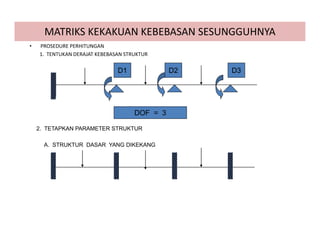
7. B. Hubungan D dengan d
d1
d2
d5 d6
d3
d4
D1 D2
D3
[d] = [ A]{D}
Diberikan D2: 1 satuan
d1 = 0
d2 = 0
d3 = 0
d4 = 1
d5 = 1
d6 = 0
Diberikan D1 : 1 satuan
d1 = 0
d2 = 1
d3 = 1
d4 = 0
d5 = 0
d6 = 0
Diberikan D3 : 1 satuan
d1 = 0
d2 = 0
d3 = 0
d4 = 0
d5 = 0
d6 = 1
0 0 0
1 0 0
1 0 0
0 1 0
0 1 0
0 0 1
[ A ] =

8. 3 MATRIKS KEKOKOHAN BATANG [ S ]
Matriks yang menyatakan hubungan gaya dalam dan deformasi
d1
- Gaya Normal
SR. L
AE
SR : Gaya normal
dn-1 dn L : Panjang batang
A : Luas Penampang
E : Modulus elastisitas bahan
dn-1 = AE/L. SR
dn = - AE/L. SR
dn =

9. - Momen Lentur
dn - 1
SRn-1
dn
SRn
akibat SRn-1 akibat SRn
dn-1 dn
dn-1 dn
dihitung dengan Conyugated Beam
Putaran sudut = Reaksi akibat bidang Momen sebagai beban dibagi EI
dn-1 dn
1/2 SRn-1. L dn 1/2 SRn.L
dn-1
dn-1 = 1/3 SRn-1. L / EI dn-1 = - 1/6 SRn. L / EI
dn = - 1/6 SRn-1. L / EI dn = 1/3 SRn L / EI

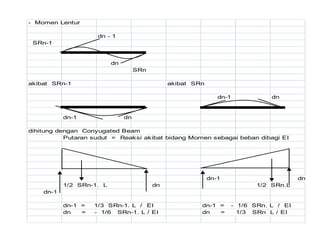
10. 2 dn-1 = 2/3 SRn-1. L / EI - 1/3 SRn. L / EI
dn = - 1/6 SRn-1. L/EI + 1/3 SRn. L/EI
2 dn-1 + dn = 1/2 SRn-1 .L / EI
SRn - 1 = 4 EI/L. dn-1 + 2 EI / L dn
analog untuk SRn
SRn = 2 EI/L. dn-1 + 4 EI / L dn
sehingga hubungan antara Momen dan deformasi dapat dinyatakan dalam bentuk matriks sbb
SRn 4 EI/L 2 EI/L dn
SRn-1 2 EI/L 4 EI/L dn-1
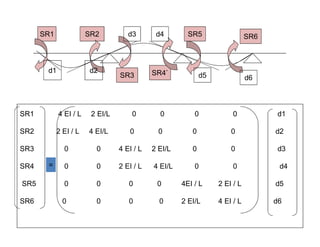
untuk balok statis tertentu sebagaimana sketsa diatas, dengan mengabaikan akibat gaya normal
SR1 4 EI/L 2 EI/L 0 0 0 0 d1
SR2 2 EI/L 4 EI/L 0 0 0 0 d2
SR3 0 0 4 EI/L 2 EI/L 0 0 d3
SR4 0 0 2 EI/L 4 EI/L 0 0 d4
SR5 0 0 0 0 4 EI/L 2 EI/L d5
SR6 0 0 0 0 2 EI/L 4 EI/L d6
[ S ]

11. SR1 4 EI / L 2 EI/L 0 0 0 0 d1
SR2 2 EI / L 4 EI/L 0 0 0 0 d2
SR3 0 0 4 EI / L 2 EI/L 0 0 d3
SR4 0 0 2 EI / L 4 EI/L 0 0 d4
SR5 0 0 0 0 4EI / L 2 EI / L d5
SR6 0 0 0 0 2 EI/L 4 EI / L d6
=
SR1 SR2 SR5 SR6
d3
SR3 SR4`
d1 d2
d4
d5 d6

12. SR1
SR2 SR5
SR6
P1
P2
SR3 SR4`
[P] = [ B] {SR}
Ternyata [ B ] = [ A ]T
P3
0 1 1 0 0 0
0 0 0 1 1 0
0 0 0 0 0 1
[ B ] =
MATRIKS KESETIMBANGAN GAYA LUAR (P) dan GAYA DALAM ( SR )

13. 3. Perhitungan Matriks GAYA luar [P]
Matriks P merupakan penjumlahan momen primer pada satu
titik kumpul
4. Menentukan matriks Kekakuan struktur
[ K ] = [ A ]T [ S ] [A ]
5. Menentukan Matriks [ K ] -1
6. Menentukan Matriks { D ] = [ K ] -1 [ P }`
7. Menentukan Matriks gaya Dalam [ SR ] = [ S ] { A ] [ D ]
8. Menentukan Momen akhir M = [ M ]f - [ SR ]

14. MATRIKS KEKAKUAN SUPERPOSISI LANGSUNG
2 5 Y
A 1 B 4
X
3 6
DENGAN MENGABAIKAN DEFORMASI AKIBAT GAYA LINTANG
Normal LINTANG MOMEN LENTUR
Normal LINTANG MOMEN LENTUR
1 2 3 4 5 6
EA/L 0 0 -EA/L 0 0
0 12 EI / L
3
6 EI / L
2
0 -12 EI / L
3
6 EI / L
2
[ KAB ] i = 0 6 EI / L
2
4 EI / L 0 - 6 EI / L
2
2 EI / L
-EA/L 0 0 EA/L 0 0
0 -12 EI / L
3
- 6 EI / L
2
0 12 EI / L
3
- 6 EI / L
2
0 6 EI / L
2
2 EI / L 0 - 6 EI / L
2
4 EI / L
KOORDINAT LOKAL

15. MATRIKS TRANSFORMASI
( Mengubah Koordinat Lokal menjadi Koordinat Global)
5
B 4 Y
2 6
1
a
Ditinjau dari sb x+ berlawanan X
A arah jarum jam
3
Z
EI
L= 5
a = 60O
1 2 3 4 5 6
Cos a Sin a 0 0 0 0
- Sin a Cos a 0 0 0 0
0 0 1 0 0 0
0 0 0 Cos a Sin a 0
0 0 0 - Sin a Cos a 0
0 0 0 0 0 1
[ TAb] =

16. HUBUNGAN MATRIKS TRANSFORMASI DENGAN MATRIKS -
KEKAKUAN
[P] i = [ K ]I [ D ]I
[P] s = [ K ]s [ D ]s
HUBUNGAN MATRIKS DIOPERASIKAN SEBAGAI BERIKUT :
[P] i = [ T ] [ P ]s
[D] i = [ T ] [ D ]s
[ T ] [ P ]s = [ K ]I [ T ] [ D ]s
[T] -1
[ T ] [ P ]s = [ T ] -1
[ K ]I [ T ] [ D ]s
[ P ]s = [ T ] -1
[ K ]I [ T ] [ D ]s
Mengingat sifat orthogonal suatu matriks transformasi
[ T ]
-1
= [ T ]
T
sehingga
[ P ]s = [ T ] T
[ K ]I [ T ] [ D ]s
[ K] s = [ T ]T
[ K ] I [ T ]
[ K ] s : Matriks kekakuan elemen batang Koord. Struktur
[ K ] i : Matriks kekakuan elemen batang Koord. Individual

17. MATRIKS KEKAKUAN STRUKTUR
Setelah Matriks Kekakuan struktur diperoleh dilakukan Pemisahan ( Partisi )
antara Matriks Pada titik yang bebas dan matriks pada titik tetap
1 2 3 4 5 6 7 8 9 10 11 12
1 k11 k12 k13 k14 k15 k16 k17 k18 k19 k110 k111 k112
2 k21 k22 k23 k24 k25 k26 k27 k28 k29 k210 k211 k212
3 k31 k32 k33 k33 k35 k36 k37 k38 k39 k310 k311 k312
4 k41 k42 k43 k44 k45 k46 k47 k48 k49 k410 k411 k412
[ K ] s = EI 5 k51 k52 k53 k54 k55 k56 k57 k58 k59 k510 k511 k512
6 k61 k62 k63 k64 k65 k66 k67 k68 k69 k610 k611 k612
7 k71 k72 k73 k74 k75 k76 k77 k78 k79 k710 k711 k712
8 k81 k82 k83 k84 k85 k86 k87 k88 k89 k810 k811 k812
9 k91 k92 k93 k94 k95 k96 k97 k98 k99 k910 k911 k912
10 k101 k102 k103 k104 k105 k106 k107 k108 k109 k1010 k1011 k1012
11 k111 k112 k113 k114 k115 k116 k117 k118 k119 k1110 k1111 k1112
12 k121 k122 k123 k124 k125 k126 k127 k128 k129 k1210 k1211 k1212
6 9 12 1 2 3 4 5 7 8 10 11
6 k66 k69 k612 k61 k62 k63 k64 k65 k67 k68 k610 k611
9 k96 k99 k912 k91 k92 k93 k94 k95 k97 k98 k910 k911
12 k126 k129 k1212 k121 k122 k123 k124 k125 k127 k128 k1210 k1211
1 k16 k19 k112 k11 k12 k13 k14 k15 k17 k18 k110 k111
2 k26 k29 k212 k21 k22 k23 k24 k25 k27 k28 k210 k211
3 k36 k39 k312 k31 k32 k33 k33 k35 k37 k38 k310 k311
4 k46 k49 k412 k41 k42 k43 k44 k45 k47 k48 k410 k411
[ K ] s = EI 5 k56 k59 k512 k51 k52 k53 k54 k55 k57 k58 k510 k511
7 k76 k79 k712 k71 k72 k73 k74 k75 k77 k78 k710 k711
8 k86 k89 k812 k81 k82 k83 k84 k85 k87 k88 k810 k811
10 k106 k109 k1012 k101 k102 k103 k104 k105 k107 k108 k1010 k1011
11 k116 k119 k1112 k111 k112 k113 k114 k115 k117 k118 k1110 k1111

18. PF KFF KFB DF
PB KBF KBB DB
DF : LENDUTAN DI TITIK BEBAS
DB : LENDUTAN DI PERLETAKAN = 0
[ PF ] = [ KFF ] [ DF ] + [ KFB ] [ DB ]
[ PB ] = [ KBF ] [ DF ] + [ KBB ] [ DB ]
KARENA [ DB ] = 0, MAKA
[ PF ] = [ KFF ] [ DF ]
[ DF ] = [ KFF ]-1
[ PF]
REKASI TUMPUAN
[ PB ] = [ KBF ] [ DF ] + [ KBB ] [ DB ]
[ PB ] = [ KBF ] [ DF ]
=
[ D]I =[Tab][D]s
Setelah deformasi struktur koordinat global diperoleh,
selanjutnya dihitung deformasi sesuai koordinat lokal

19. Selanjutnya dihitung Gaya dalam setiap batang, yang
bekerja pada ujung batang
[ SR ]I = [ KAE ]I [ D]i
2 5
A 1 B 4
3 6
SR1
SR3
SR2 SR5
SR4
SR6
Terakhir menghitung Momen, Gaya Lintang dan Gaya
Normal pada titik kumpul
[ Ma] = [ SR3 ] - [ Mf]
[ Da ] = [ SR2 ] - [ Df]
[ N a] = [ SR1 ] - [ Nf]
[ Mb ] = [ SR6 ] - [ Mfb]
[ Db ] = [ SR5 ] - [ Dfb]
[ N B] = [ SR4 ] - [ Nfb]

20. SEKIAN
SAMPAI KULIAH
BERIKUTNYA