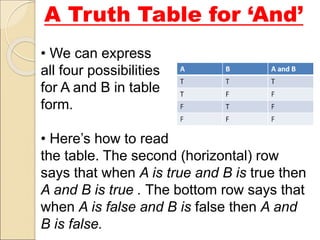
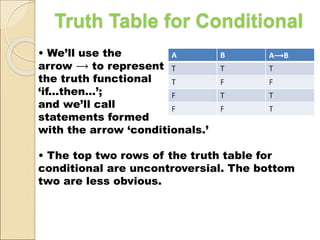
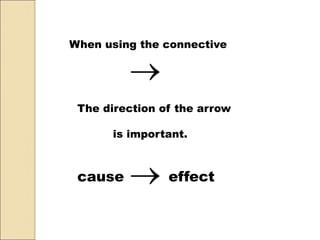
This document discusses logical connectives and truth functions. There are five basic connectives: conjunction, disjunction, negation, implication, and equivalence. Truth functions combine sentences in ways that the truth value of the longer sentence is determined by the truth values of the parts. Each connective is represented by a symbol and has a corresponding truth table that shows the possible truth value combinations of the statements joined by the connective.

2. The words and phrases to form compound
statements are called connectives.
There are five basic connectives :-
1) Conjunction
2) Disjunction
3) Negation
4) Implication or Conditional
5) Equivalence or Biconditional

3. Truth Functions
• Declarative sentences (statements) are
either true or false but not both. They cannot
be neither.
• Whether a sentence is true or false
determines its truth value.
• Functions take input values to unique output
values . That is, the input values determine the
output values.
• There are some ways of combining
sentences into longer ones so that the truth
value of the longer sentence is determined by
the truth value of the parts that were
combined to form it.
• So, we’ll call the connectives , that combine
sentences in this way that they form truth
functions.

4. 1) CONJUNCTION
 Symbol used :-
 Connective word :- and
 Its symbolic form :- p q
 ‘And’ is often a truth functional connective
. Inserting ‘and’ between two statements
gives a longer sentence , the truth of
which is determined by the truth of the
parts.
 If p and q are both true then the longer
sentence is true. If either of p or q is false



5. p : John passes.
h : John is happy

This symbol replaces
the word “AND”
John passes AND John is happy
p h

6. • We can express
all four possibilities
for A and B in table
form.
• Here’s how to read
the table. The second (horizontal) row
says that when A is true and B is true then
A and B is true . The bottom row says that
when A is false and B is false then A and
B is false.
A Truth Table for ‘And’

7. 2) DISJUNCTION
 Symbol used :- V
 Connective word :- or
 Its symbolic form :- p V q
Examples :-
Either Lenny or Manny left for Bermuda.
(L=Lenny left for Bermuda. M=Manny left
for Bermuda.)
Translation : L V M

8. Truth Table for Disjunction
• The four possibilities
For sentences
A and B are
represented by the
left two
(vertical) columns.
• The top row of Ts and Fs is the possibility
where A is true and B is true. On that
possibility ‘A V B’ is true.
• The bottom row is the possibility where A and
B are both false. In that case ‘A V B’ is also
false.
• Disjunction differs from conjunction on the
middle two rows.

9. 3) NEGATION
 Symbol used :- ~
 Connective word :- not
 Its symbolic form :- ~ p
 Prefixing a statement with ‘it is not the
case that’ flips the truth value.
Examples :-
 Manny left but Lenny did not leave.
(L=Lenny left for Bermuda. M=Manny
left for Bermuda.)
Translation : M ~L

10. Truth Table for Negation
• The symbol to represent that truth
function is ‘ ~ ’. The symbol is called ‘tilde’
or just ‘squiggle’.
• Unlike the other connectives, tilde
doesn’t connect two sentences. It just flips
the value of a single sentence.

11. s : John studies.
John does NOT study:
s
This symbol negates the
statement it precedes
~
~
Example :-

12. 4) IMPLICATION ( or CONDITIONAL )
 Symbol used :-
 Connective word :- if........then
 Its symbolic form :- p q
 Some uses of ‘if..then…’ are truth functional
and some are not .
 Consider: If you whistle loudly then the dog will
come. There’s really just one scenario that
shows the sentence to be false: whistle loudly
and have the dog not come. If you whistle and
the dog comes then the sentence was true. If
you don’t whistle then no matter whether the
dog comes or not, you didn’t show the



13. s : John studies.
p : John passes. 
This symbol replaces
the connective “if … then”
IF John studies THEN John passes.
s p
Example :-

14. Truth Table for Conditional
• We’ll use the
arrow ⟶ to represent
the truth functional
‘if...then…’;
and we’ll call
statements formed
with the arrow ‘conditionals.’
• The top two rows of the truth table for
conditional are uncontroversial. The bottom
two are less obvious.

15. Order Matters
• Notice on the table that the order of A and B
matter. A true and B false yields a different
value than A false and B true. So, unlike
conjunction and disjunction where order
doesn’t matter, we have a different names for
the different parts of the conditional.
• For A ⟶ B, A is called the ‘antecedent’ and B
is called the ‘consequent’.
• There are many English expressions that can
be translated as conditionals. The trick to
symbolizing them correctly is to identify the
antecedent and the consequent.

16. When using the connective

The direction of the arrow
is important.
cause effect

17. 6) EQUIVALENCE ( or BICONDITIONAL
)
 Symbol used :-
 Connective word :- if and only if
 Its symbolic form :- p q
 If we say ‘ A if B and A only if B ’ or in other
words ‘A if and only if B’ we could translate that
as ‘(B⟶A)&(A⟶B)’.We’ll use the double arrow
⟷ (or the triple bar ) as an abbreviation for that.
Also, we’ll call sentences formed by using the
double arrow ‘biconditionals’.
 Sometimes you see ‘iff’ between two sentences.
It’s not a typo. It’s an abbreviation for ‘if and
only if.’ So ‘A iff B’ would be translated as



18. s : John studies.
h : John is happy 
This symbol replaces
the words “if and only if”
John is happy IF AND ONLY IF John studies.
h s
Example :-

19. Truth Table for Biconditional
• Think of the
biconditional as
saying that two
sentences have
matching truth value.
The longer sentence
is true when both parts
are true or when both parts are false.
• Notice that order doesn’t matter ; so we don’t have
special names for the letter that comes first.
Unlike regular conditional, A ⟷ B is equivalent to B⟷A.
• The sentence ‘A⟷B ‘is just an abbreviation for the more
complicated sentence ‘(B⟶A)&(A⟶B)’.

20. John is happy ONLY IF he studies.
John is happy IF he studies.
John is happy IF AND ONLY IF he studies.



Example :-