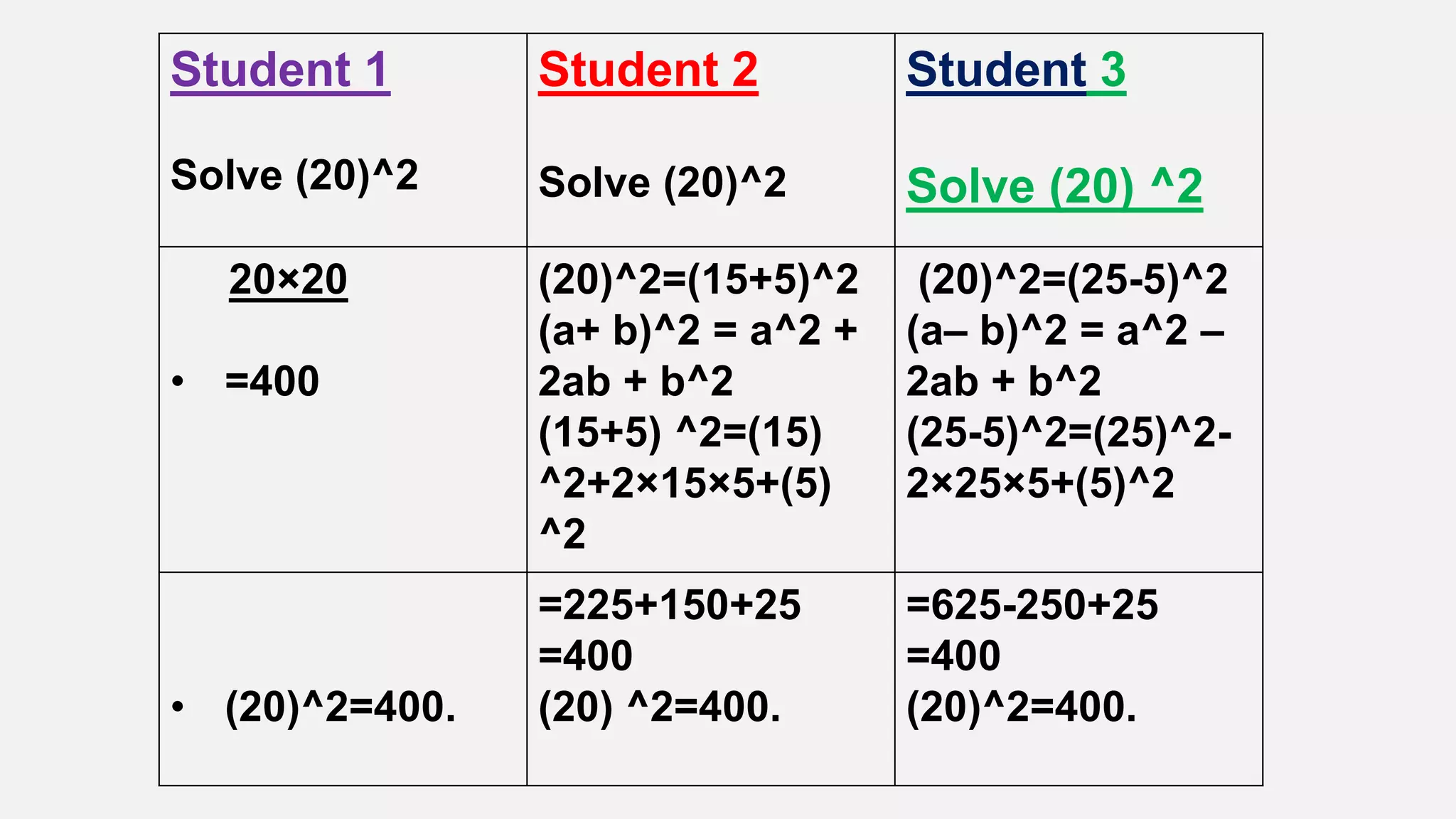
The document discusses mathematical processes including reasoning, argumentation, and justification, emphasizing their roles in problem solving and logical thinking. It defines various types of reasoning, such as inductive and deductive, and highlights examples to illustrate these concepts. Additionally, it describes the importance of mathematical argumentation and justification in reinforcing understanding and supporting problem-solving skills among students.

1. GOVERNMENT COLLEGE OF
TEACHER EDUCATION
CHITRADURGA, 577501

2. MATHEMATICAL PROCESS.
Mathematical process
means thinking and
reasoning, calculation
and salvation of
mathematical problems
by mathematical methods.
Ex:- Derive (a-b) ^3

3. • (a-b) ^3= (a-b)(a-b)(a-b)} Thinking.
•
• (a-b)^3 = (a^2-2ab+b^2) (a-b) [Since, (a-b)^2 =
a^2+b^2-2ab)} (Reasoning) .
•
• (a-b)^3 = a^3-2a^2b+ab^2-a^2b+2ab^2-b^3
• (a-b)^3 = a^3-3a^2b+3ab^2– b^3
• (Calculation)
• Therefore, the formula for (a-b)^3 is a^3-
3a^2b+3ab^2– b^3.
•
• The above formula can also be written as:
•
• (a-b)^3 = a^3-3ab(a-b) – b^3}( Solution) .

4. MATHEMATICAL PROCESS
INCLUDES
• 1) Reasoning.
• 2) Logical thinking.
• 3) Problem solving.
• 4) Connecting.
• 5) Problem posing.
• 6) Abstraction.
• 7) Argumentation.
• 8) Justification. Etc

5. MATHEMATICAL PROCESSES.

6. MATHEMATICAL PROCESS.
• 1) Mathematical reasoning.
• 2) Mathematical argumentation.
• 3) Mathematical justification.

7. MATHEMATICAL REASONING.
• Mathematical reasoning happens through
making conjectures, investigating, and
representing and finding and explains and
justifying conclusions.
• Reasoning can be thought of as the process of
drawing conclusions on the basis of evidence or
stated assumption and sence making can be
defined as developing and understanding of a
situation, context, or concept by connecting it
with existing knowledge.

8. MATHEMATICAL REASONING.
The (NCTM) National
council of teacher of
mathematics defines
reasoning as the “A
productive way of
thinking that
becomes common in
the process of
mathematical inquiry
and sence making”.
Ex:- Solve (20)^2

9. Student 1
Solve (20)^2
Student 2
Solve (20)^2
Student 3
Solve (20) ^2
20×20
• =400
(20)^2=(15+5)^2
(a+ b)^2 = a^2 +
2ab + b^2
(15+5) ^2=(15)
^2+2×15×5+(5)
^2
(20)^2=(25-5)^2
(a– b)^2 = a^2 –
2ab + b^2
(25-5)^2=(25)^2-
2×25×5+(5)^2
• (20)^2=400.
=225+150+25
=400
(20) ^2=400.
=625-250+25
=400
(20)^2=400.

10. EXAMPLE OF REASONING.
Ex:- Solve 18+27=__+29
Here twenty nine is two more than 27 , So the
number which is added has to be two less
than 18 to making the eqution.
Instead of adding 18+27 then figuring out the
number to add 29 to get 45,simplify the
calculation by comparing the numbers on both
sides one who realised 29 is two more than
27.So the number added had to be two less
than 18 that is 16.

11. MATHEMATICAL
REASONING TWO TYPES.
• 1) Inductive reasoning.
• 2) Deductive reasoning.
• Inductive reasoning:-Inductive reasoning is a
logical process in which multiple premises, all
believed true or found true most of the time,
are combined to obtain a specific conclusion.
• Inductive reasoning is a method of logical
thinking that combines observations with
experiential information to reach a
conclusion.

12. INDUCTIVE REASONING.

13. INDUCTIVE REASONING.

14. INDUCTIVE REASONING.

15. DEDUCTIVE REASONING.
Deductive reasoning is a logical process
in which a conclusion is based on the
concordance of multiple premises that are
generally assumed to be true.
Example
• All numbers ending in 0 or 5 are divisible
by 5.
• The number 35 ends with a 5.
• so it must be divisible by 5.

16. DEDUCTIVE REASONING.

17. DEDUCTIVE REASONING.

18. DIFFERENCE BETWEEN INDUCTIVE
AND DEDUCTIVE REASONING

19. ADVANTAGES OF MATHEMATICAL
REASONING.
• Helps children to think logically and
make sense of mathematics.
• Help children to test hypothesis.
• Help chldren to make predictions.
• Helps children to explain their
thinking.

20. MATHEMATICAL ARGUMENTATION.

21. MATHEMATICAL
ARGUMENTATION.
A mathematical
argumentation is
sequence of statements
and reasons given with
the aim of
demonstrating that a
claim is true or false.
OR
The act or process of
forming reasons and of
drawing conclusions and
applying them to a case in
discussion

22. MATHEMATICAL
ARGUMENTATION EXAMPLE
• Statement 1:- Numbers ending with 0 and 5 are
divisable by 5) How?
• Statement 2:-Numbers ending with 0 divisable
by 10.} How?
• Statement 3:- Numbers ending with 3 and 9
divisable by 2] How?
• Statement 1:-True
• Statement 2:-True
• Statement 3:-False

23. MATHEMATICAL
ARGUMENTATION.
Example

24. MATHEMATICAL
ARGUMENTATIONS ARE LIKE
THIS.
• How does that look
like?
• What happened
after?
• Can you tell me
why?
• How does this fit?

25. MATHEMATICAL ARGUMENTATION
ARE LIKE THIS.
• Can you explain?
• What happened before?
• What would happen if you used this number?
• What would change if.....
• Show me where.....
• What could you add to strengthen this part?
• How would that work?

26. ADVANTAGES OF
MATHEMATICAL
ARGUMENTATION.
• Discover new mathematical ideas.
• Argumentation supports for the
conclusion.
• Contributed to the class understanding.
• Tool for student reasoning.
• Provides evidence and reasoning for new
idea.

27. MATHEMATICAL JUSTIFICATION.
• Mathematical justification in a mathematical
setting teaches a important writing style,
writing a brief, information packed statement
that gives the reader a solid reason to
believe your conclusion, without wasting a
readers time.
• OR
• Mathematical justification is the use appropriate
mathematical language to give reasons for the
particular approach used to solve a problem.

28. EXAMPLE
• Determine when the first equation is cheaper than
the second
• C = 40t+200
• C=30t+300
• Developing a solution
• Students will work on the solution of the problem.
Either graphically, or by solving simultaneous
equations, the time for which costs are equal is 10
hours.
•
• Note: The time for which the first rate is more than
the second is any time greater than 10 hours.

29. MATHEMATICAL JUSTIFICATION
PROPERTIES.

30. HOW TO JUSTIFY EQUATION

31. ADVANTAGES OF MATHEMATICAL
JUSTIFICATION.
• Students learn better when they self justify and
and explain the solution.
• It supports logical reasoning and analytical
thinking.
• It improves problem solving skills.
• Teachers need to know how students arrive at
their answer.
• Explanations encourage students to explain the
why and not just the how.

32. •Thank you....